傅里叶变换的行波型中空超声电机的系统效率*

牛子杰，孙志峻，吴金涛，张 军，张激扬，梁大志

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (2.北京控制工程研究所 北京，100190)



傅里叶变换的行波型中空超声电机的系统效率*

牛子杰1，孙志峻1，吴金涛2，张 军1，张激扬2，梁大志1

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (2.北京控制工程研究所 北京，100190)

由于行波型中空超声电机的驱动信号为高压、高频信号，因此，由行波型中空超声电机及其驱动器组成的系统的各级功率与效率不容易获取，这些因素均影响到后续对行波型中空超声电机性能的研究。针对此问题，首先，通过傅里叶变换的方法对超声电机驱动信号进行处理，构建了电机及其驱动系统各级效率的计算方法；然后，通过实验获取了行波型中空超声电机及其驱动器组成的系统的效率，并进一步研究了驱动频率、驱动电压及谐振匹配点对系统效率的影响。实验表明：驱动频率越靠近谐振频率，系统总效率越高；驱动电压越大，系统总效率越高；驱动电路匹配的谐振点远远高于电机机械谐振频率，使得驱动信号频率介于电路谐振频率和机械谐振频率之间时系统的效率最高。

傅里叶变换； 超声电机； 系统效率； 谐振频率； 匹配电路

引 言

与电磁电机相比，超声电机具有大力矩、低转速、能量密度大、响应速度快、定位精度高、无电磁干扰、断电自锁等优点。随着光学工程、航空航天和精密制造等技术的快速发展，超声电机这些优点越来越突出，这使得对超声电机的需求更加迫切[1-2]。行波型中空超声电机(简称中空电机)作为一种特殊的微特电机，在继承了常见超声电机的特点以外，中空的结构更拓宽了其使用范畴[3]。行波型中空超声电机与其驱动器组成的是一个机电系统。由于此种电机与普通的电磁电机原理及结构差异较大，所以该种电机的驱动器与普通电磁电机驱动器的差异也比较大。

国内外很多学者都对行波超声电机驱动功率进行了研究。上羽贞行等[4]对佳能环状超声电机进行了研究，总结出该种电机的等效电学模型。祖家奎等[5]研究了定子的电学特性、驱动方式及其振动性能之间的关系，提出应根据电机的输出功率选择合适的工作频带和驱动方式。史敬灼等[6]研究了行波电机驱动电路的匹配方式，给出了超声电机串联电感匹配电路的设计原则。然而，这些研究大部分着眼于超声电机的某些局部，如电机本体或电机的驱动器，而对超声电机及其驱动器组成的机电一体化系统整体的研究较少，从功率传递及机电一体化系统效率角度对超声电机系统研究的更少。其主要存在如下问题：a.超声电机驱动信号为高频，是高压信号，因此获取系统各级相关功率及效率目前尚无成熟方法；b.驱动频率、驱动电压及电路谐振匹配点对电机系统效率的影响目前研究较少。

针对笔者在文献[7]中提出的一种中空式行波超声电机和文献[8]提出的一种并联电容式超声电机驱动器的基础上进行研究。首先，分析了超声电机能量传递机理；其次，对超声电机驱动信号进行实验和数据采集；接着，在Matlab环境下对数据进行傅里叶变换处理；最后,分析数据得到此种中空电机及其驱动系统相关部分功率随着负载变化的变化情况。

1 中空电机及其驱动器拓扑结构

1.1 中空电机结构

本研究的超声电机是一种中空式的超声电机，其结构如图1所示。

图1 电机结构

根据图1所示的电机结构可以看出:柔性转子通过贴在表面的摩擦片与定子接触；而柔性转子下方通过螺纹与预压力螺母连接；预压力螺母通过轴承给柔性转子施加拉力[9]。

1.2 并联电容电路拓扑结构

笔者使用的驱动器为文献[8]中所描述的驱动器，其拓扑结构如图2所示。中空电机与驱动器之间通过4根电源线连接，其中2根驱动信号分别为sin信号和cos信号，另外两路为地信号和孤极电压信号。图2所示为sin信号或者cos信号中的某一路电源信号，中空电机陶瓷片中的一项并联于OUT和COM之间。

图2 并联电容驱动器拓扑结构

图3所示的是中空电机与驱动器之间连接的简图。其中：L1和L2分别为驱动器A相和B相的变压器副边电感；C1和C2分别为驱动器A相和B相的并联匹配电容；CA和CB分别为中空电机A相和B相的静态电容。一般情况下L1=L2，C1=C2，CA=CB。

图3 中空电机与驱动器连接简图

2 中空电机运行机理

2.1 定子行波的产生

笔者论述的中空行波超声电机的振动主体(即定子)为一带支撑板的圆环，上面有齿状结构，其振动方程没有解析表达式。为便于原理性分析，可把它简化成一圆板状结构，如图4所示。

图4 定子形状

根据弹性动力学理论可知，对于一个平面圆板，存在如图5所示的弯曲振动模态，其振型一般称之为B0n，其中n为弯曲振动的波数[10-13](此例图中波数为11)。

图5 定子模态

用某振型函数φA(r,θ)来对该振型加以描述，称之为A相振型

φA(r,θ)=R(r)cos(nθ)

(1)

其中：R(r)为归一化的不同半径处的垂向振幅函数。

在圆板最外缘R(r)值取为1，即

R(rmax)=1

(2)

设该振型的模态坐标为

qA(t)=WAcos(ωnt)

(3)

其中：ωn为对应该振型的固有频率。

A相的驻波振动方程为

wA(r,θ,t)=φA(r,θ)qA(t)=WAR(r)cos(nθ)cos(ωnt)

(4)

由于圆板是轴对称的，与A相振型在空间上相差任意角度的振型都是该模态的主振型[14]，取与其相差π/2的正交振型，该振型称之为B相振型

φB(r,θ)=R(r)sin(nθ)

(5)

当B相振动的模态坐标取为

qB(t)=WBsin(ωnt+α)

(6)

则B相的驻波振动方程为

wB(r,θ,t)=φB(r,θ)qB(t)=WBR(r)sin(nθ)sin(ωnt+α)

(7)

由线性波的叠加原理，A和B两相驻波可叠加成如下振动[15]

(8)

根据式(8)可知，圆板此时的振动由正向行波cos(nθ-ωt)、反向行波cos(nθ+ωt)和驻波cosωt组成。

1) 当α=0，WA=WB=W0时，即B相与A相同频、等幅、空间及时间上都超前π/2时，此二驻波可叠加为一个正向(逆时针)行波

w(r,θ,t)=ξ0R(r)cos(nθ-ωt)

(9)

2) 当α=π,WA=WB=W0时，即B相与A相同频、等幅、空间超前π/2、时间滞后π/2时，此二驻波可叠加为一个反向(顺时针)行波

w(r,θ,t)=ξ0R(r)cos(nθ+ωt)

(10)

3) 当α=π/2时，圆环板中只有驻波，不形成行波。

2.2 压电陶瓷片的极化配置

上面讨论了行波产生的条件，为了满足这些条件，以便在超声电机定子中激发出所期望的理想行波，在定子的结构设计、压电陶瓷的极化、配置以及施加交变电压等方面也必须满足特定的条件。压电陶瓷片极化[16]如图6所示。

1) 为产生A,B两相驻波并满足空间相位差π/2，通常按照图6方式进行压电陶瓷的极化和配置，即在A,B两相极化了的压电陶瓷间留有λ/4和3λ/4的空间。图6中孤极虽然极化，但不是用来激励定子的，其上不施加交变电压。当其随定子振动时由于逆压电效应在孤极上会产生交变电压，通过该电压可判断超声电机的工作状态，因此该电压可供驱动和控制电路用作反馈信号，通常称之为孤极反馈。图7,8分别为A相和B相激励驻波。

2) 为保证时间的相位差，需对A，B两相压电陶瓷分别激振，一个施加sin相交变电压的同时，另一个施加cos相交变电压。

图6 压电陶瓷片极化

图7 A相激励驻波

图8 B相激励驻波

3 傅里叶变换

傅里叶变换将满足一定条件的某个函数表示成三角函数(正弦、余弦函数)或者它们积分的线性组合。傅里叶变换是数字信号处理领域一种很重要的算法，其原理表明，任何连续测量的时序或信号都可以表示为不同频率的正弦波信号的无限叠加。根据该原理创立的傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

3.1 傅里叶变换公式

由上面分析可知，中空电机的输入信号为高频信号，由于压电陶瓷片需要的驱动电压较高，因此高频驱动信号在经过变压、滤波之后变成了高频、高压信号。由于超声电机为容性负载，电路无法做到完美匹配，因此最后得到的电机驱动信号为含有较多杂波的非正弦高频、高压信号，如图9所示。该种信号如果不经过傅里叶变换，将其分解为谐振频率的多次谐波信号，要计算得到电路中各级的功率及效率比较困难。因此,对于电机驱动信号进行傅里叶变换是后续电路效率及功率研究的基础。

图9 示波器显示的电压与电流信号

中空电机A，B两项陶瓷片分别施加激振电压，一个施加正弦相交变电压信号(图9中绿色曲线)的同时，另一个必须施加余弦相交变电压信号(图9中黄色曲线)。图9中的红色曲线为与黄色曲线对应的电流信号。笔者将中空电机A，B两项的电压和电流信号分别进行傅里叶变换，用到的傅里叶级数为

(11)

其中：x(t)为电压或者电流实时信号；a0为直流分量；an和bn为n次谐波的系数；ω0为基频。

参数a0，an和bn为

(12)

利用辅角公式将式(11)中的cos谐波和sin谐波进行合并，可得

(13)

其中：a0为信号均值，是直流分量；An为N次谐波的幅值；nω0为N次谐波的频率；φn为N次谐波的相角。

其中，参数An和φn为

(14)

3.2 中空电机及其驱动系统各级效率的获取

中空电机及其驱动器组成的机电系统，在负载条件下工作框图如图10所示。

图10 系统能量传递框图

由图10可知，中空电机及其驱动器组成的机电系统在工作过程中涉及到的效率分别包括驱动器效率、中空电机效率和机电系统总效率，涉及到的功率分别为系统输入功率、电机输入功率和系统输出功率。下面分别给出相关功率及效率的计算方法。

系统输入功率主要通过直流电源获取电压和电流得到，具体如下

Pin=UinIin

(15)

电机输入功率与驱动器输出功率相同。如上所述，通过傅里叶变换，得到电压和电流信号的各频率点的分量，然后计算每个频率点的有功功率，再将这些功率相加，最后获得电机输入功率。笔者在数据分析过程中获取了傅里叶变换得到的电压和电流信号的直流分量、一次谐波分量、二次谐波分量和三次谐波分量。分别针对每种信号求得相关的功率，具体如下

(16)

其中：P0，P1，P2，P3分别为直流分量功率、一次谐波分量功率、二次谐波分量功率和三次谐波分量功率；φU为电压相位角；φI为电流相位角。

在获得各谐波分量的功率之后，可获得电机输入功率Pdin。由于超声电机驱动信号为两路，因此输入功率要乘以2

Pdin=2(P0+P1+P2+P3)

(17)

系统输出功率主要通过输出扭矩与转速获得，本系统输出功率为

Pout=2πToutnout/60

(18)

其中：Pout为系统输出功率；Tout为电机输出扭矩；nout为电机输出转速。

在获得相关功率之后，机电系统各模块的效率计算相对比较简单。式(19)为驱动器效率，式(20)为电机效率，式(21)为电机及其驱动系统总效率

(19)

(20)

(21)

4 实验及数据分析

4.1 实验环境

实验需要测试的数据包括直流电源的电压和电流、电机输入的两路驱动电压和电流、电机输出转速和扭矩、孤极反馈电压。实验装置如图11所示。为了消除温度对电机性能的影响，保证数据的可靠性，本实验在洁净房进行，室温为25℃。在电机进行实验测试之前,先让电机空转10 min左右,以保证电机温度达到平衡。

图11 实验设备

实验装置中：直流电源用于提供能量及测量输入电压和电流；测功机用于提供负载扭矩和测量电机输出扭矩和转速；示波器用于测量电机输入电压、电流计孤极电压；电流探头用于辅助示波器测量电机输入电流。

4.2 数据处理

为了获得较真实的结果，本实验在每一个负载扭矩下采集2 000组电机输入的电压和电流信号,然后利用三次傅里叶变换将每个扭矩点的电压和电流分别分解为直流分量、一次谐波分量、二次谐波分量和三次谐波分量，再分别计算功率，将计算得到电机输入总功率。相关数据处理流程如图12所示。

图12 数据处理流程

数据处理包括单点处理和批量处理。单点处理是指获得电机在某一个扭矩负载下分解得到电机输入信号的各谐波分量，软件界面如图13所示。

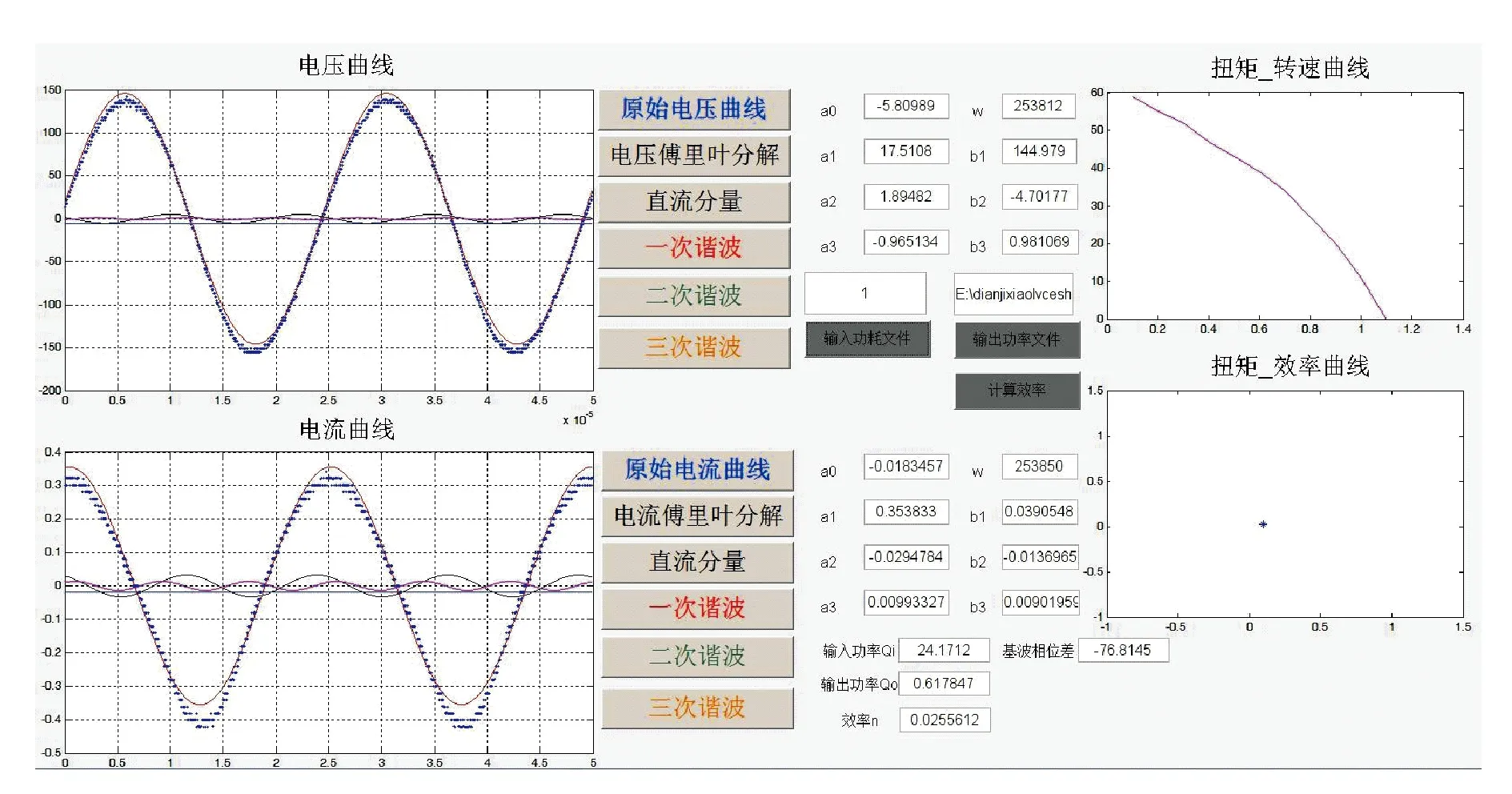
图13 单点数据处理界面

由于每个扭矩点均记录了2 000组数据，在整个电机性能测试实验中数据量非常大，因此笔者通过批量数据处理软件将电机的扭矩实验数据批量处理为一个个表单的形式。

4.3 数据分析

笔者主要通过傅里叶变换的方法获取了普通实验方法较难获取的超声电机输入功率，然后通过效率计算公式获得了中空电机及其驱动系统各级效率及整体效率，同时还对驱动频率、驱动电压、谐振匹配点对中空电机及其驱动系统的效率影响进行了研究。本实验所用的电机为70中空电机，其谐振频率为39 500 Hz，正常驱动电压峰峰值为400 V。

4.3.1 驱动频率对系统效率的影响

行波超声电机调频调速是最常见的一种形式，电机及其驱动系统在不同驱动频率下效率如何变化也成为关注的焦点。实验获取了70中空电机及其驱动器在不同的驱动频率下的系统总效率，实验结果如图14所示。由图可知,中空电机及其驱动系统总效率受到驱动频率的影响较大，驱动频率越靠近谐振频率，电路总效率越高，电机输出扭矩越大。

图14 驱动频率对系统效率的影响

4.3.2 驱动电压对系统效率的影响

行波型超声电机调压调速也是一种常见的调速形式。笔者研究了70中空电机在40 500 Hz的固定频率下驱动电压峰-峰值在250～400 V变化时系统的输出功率的变化情况,实验结果见图15。

图15 驱动电压对系统效率的影响

由图15可知，中空电机及其驱动系统总效率受到驱动电压的影响较大，驱动电压越大，电路总效率越高，电机输出扭矩越大。驱动电压往往受到压电陶瓷片的耐压阀值限制，不能太大。

4.3.3 谐振匹配点对系统效率的影响

根据参考文献[16-17],行波超声电机机电系统理想的匹配条件是匹配后电路的电纳值为零。对于本研究的70中空超声电机及其驱动系统，结合图3可知电路匹配应满足

(22)

笔者针对70中空电机及并联电感匹配的驱动器做了谐振匹配点对系统效率的影响研究。其中变压器副边电感、压电陶瓷片静态电容为常量，Lp=576 μH，Ca=11 nF。

电机机械谐振频率为39 500 Hz，分别匹配电容C1,代入式(22)可得到谐振电路的谐频率,如表1所示。同时在驱动电压峰-峰值为400 V、驱动频率为40 200 Hz下分别测试3种系统的效率,可得到图16所示曲线。

表1 匹配电容与谐振频率

图16 3种匹配点系统效率

由图16可知,驱动电路匹配的谐振点远远高于电机机械谐振频率，使得驱动信号频率介于电路谐振频率和机械谐振频率之间时系统的效率最高。

5 结 论

1) 驱动频率越靠近谐振频率，电路总效率越高，电机输出扭矩越大。

2) 驱动电压越大，电路总效率越高，电机输出扭矩越大。

3) 驱动电路匹配的谐振点远远高于电机机械谐振频率，使得驱动信号频率介于电路谐振频率和机械谐振频率之间时系统的效率最高。

[1] 周丽平，孙志峻，张泉，等．一种应用正态分布理论的直线超声电机精密定位控制方法[J]．中国电机工程学报，2012，32(27)：60-65．

Zhou Liping， Sun Zhijun， Zhang Quan， et al． A precision alignment control method of linear ultrasonic motors using the normal distribution theory[J]． Proceedings of the CSEE，2012，32(27)：60-65． (in Chinese)

[2] 赵淳生．超声电机技术与应用[M]．北京：科学出版社，2007：1-19．

[3] 赵淳生．世界超声电机技术的新进展[J]．振动、测试与诊断，2004，24(1)：1-5．

Zhao Chunsheng． Recent propress in ultrasonic motor techniques[J]． Journal of Vibration， Measurement & Diagnosis，2004，24(1)：1-5. (in Chinese)

[4] 上羽贞行，富川义郎．超声波马达理论与应用[M]．上海：上海科学技术出版社，1998：55-58．

[5] 祖家奎，赵淳生．超声电机定子的驱动方式及其振动响应特性[J].压电与声光，2006，28(1)：93-95．

Zu Jiakui， Zhao Chunsheng． Drive modes of stator of traveling wave ultrasonic motors and its vibration responses [J]． Piezoelect Rics & Acoustooptics，2006,28(1)：93-95． (in Chinese)

[6] 史敬灼，肖隽亚．超声波电动机串联电感匹配电路研究[J]．电机控制与保护，2008，27(12)：31-34．

Shi Jinzhuo， Xiao Juanya． The research of the ultrasonic motor series inductance matching circuit[J]． Motor Control and Protection，2008，27(12)：31-34． (in Chinese)

[7] 牛子杰，孙志峻，丁庆军，等．定子完全固定的中空式超声电机：中国，201320014338．3 [P]．2013-09-11．

[8] 梁大志，张军，赵淳生，等．一种超声电机双PWM功率驱动拓扑结构：中国，201210451717.9 [P]．2012-11-13．

[9] 牛子杰，孙志峻，陈超，等．基于响应面模型与自适应遗传算法的中空型行波超声电机柔性转子结构优化[J]．中国电机工程学报，2014，19(35)：62-64．

Niu Zijie， Sun Zhijun， Chen Chao, et al． Optimization of the rotor structure of a hollow traveling wave ultrasonic motor based on response surface methodology and self-adaptive genetic algorithm[J]． Proceedings of the CSEE，2014，19(35)：62-64. (in Chinese)

[10]李东旭．高等结构动力学[M]．长沙：国防科技大学出版社，1997:47-52.

[11]徐芝纶．弹性力学[M]．北京：高等教育出版社，1990:25-28.

[12]曹志远．板壳振动理论[M]．北京：中国铁道出版社，1989:34-36.

[13]Nesbitt W I, Andrew J. Modeling of a piezoelectric rotary ultrasonic motor[J]. IEEE Transactions Ultrasonics Ferroelectrics & Frequency Control, 1995,42(2):210-224.

[14]Jorg W. Contact mechanics of piezoelecctric ultrasonic motors[J]． Smart Materials and Structures, 1998(7):369-381.

[15]Zeng Jinsong， Chen Chao， Zhao Chunsheng. An effective technique for modifying modal frequencies of stator[C]∥The 2nd International Workshop on Piezoelectric Materials and Applications in Actuators. Paderborn,Germany: [s.n.],2005:456-466.

[16]林书玉.超声换能器的原理及设计[M].北京：科学出版社，2004:35-38.

[17]陈永校，郭吉丰.超声波电动机[M].杭州：浙江大学出版社，1994:22-25.

10.16450/j.cnki.issn.1004-6801.2015.06.002

*国家自然科学基金资助项目(51175264)；高校基本科研业务费科研基地创新基金资助项目(NJ20140026)

2014-11-25；

2014-12-28

TM359.4； TP273； TH113.1

牛子杰,男，1985年10月生，博士研究生。主要研究方向为行波超声电机及其驱动控制系统。 E-mail：328920539@qq．com