基于ANSYS的气瓶运输车车架轻量化设计研究
□ 张俊杰 □ 战 凯 □ 张文明 □ 姜 勇
1.北京科技大学 机械工程学院 北京 100083
2.北京矿冶研究总院 北京 100160
3.山东黄金集团有限公司 济南 250100
车架是整车的基体,承受着来自路面及装载的各种载荷作用,成为一个承受着复杂空间力系的框架结构,车架变形主要表现为弯曲和扭转两种状态[1-4]。由于气瓶运输车车架是在现有集装箱车架中选型,没有进行针对性的结构优化和轻量化设计,车架自重占气瓶运输车质量比例比较大,因此减轻车架自重对气瓶运输车的轻量化具有重要意义。笔者以气瓶运输车车架为研究对象,运用ANSYS软件对其进行静力学分析。根据分析结果,以纵梁轻量化为优化目标进行结构优化设计,获取了车架最优尺寸参数,实现了该车架的轻量化设计。
1 气瓶运输车基本结构
气瓶运输车的主要结构如图1所示,整车尺寸为12 200 mm×2 500 mm×1 780 mm,车架采用骨架式结构,由主纵梁和若干横梁组成,质量为3 368 kg。

▲图1 气瓶运输车结构图

▲图2 车架三维模型
2 车架的静力学计算分析
静力学分析主要是分析车架在静载条件下的应力和变形,一方面使车架在所承受的载荷作用下,各部分的应力和变形不超过允许的范围,另一方面通过静力分析,调整各部分的应力分布,使应力达到均衡,最大限度地利用材料,降低制造成本[5]。
2.1 有限元模型的建立
有限元模型是进行轻量化设计的基础,它既要如实反映车架的重要力学特性,又要尽可能采用少的单元和简单的单元形态,以保证较高的计算精度和运算速度[6~7]。 本文采用SolidEdge软件建立车架的几何模型,通过SolidEdge与ANSYS的接口程序将实体模型导入到ANSYS中,对模型调整修复,得到车架的有限元模型,如图2所示。
网格划分是建立有限元模型的重要环节,网格的大小及疏密程度应根据求解问题的类型及目的、计算精度和计算机的运行速度等综合考虑。如果网格过于粗糙,则可能包含严重错误;如果网格过于细密,则浪费资源,花费过多的计算时间。本文设定单元的控制尺寸为50 mm,共有246 848个单元,车架的整体有限元模型如图3所示,局部网格放大图如图4所示。
2.2 典型工况的计算分析
根据气瓶运输车的实际运行情况,本文主要选择两种典型工况进行计算。一是弯曲工况,模拟气瓶运输车满载时在水平路面上的行驶情况,此时所有车轮处于同一平面内,车架主要承受弯曲载荷。二是扭转工况,模拟气瓶运输车满载时在不平路面上行驶的情况,左前轮悬空,其它各轮保持水平状态不变。
2.2.1 弯曲工况计算
车架结构在静载条件下的载荷主要包括结构自重、瓶组和连接装置质量、充装气体质量三部分。结构自重通过钢的密度以惯性力的方式加载,瓶组和充装气体的质量通过前端立板和后端操作舱加载到车架上,车架中间与瓶组不接触。前端支撑板和后端操作舱质量不相等,计算时前端横梁加载0.72 MPa,后端两横梁加载0.38 MPa。
弯曲工况的约束处理为:约束牵引座 X、Z方向平移自由度(X为车辆行驶方向,Z为垂直车架方向),同时在车架纵梁与悬架接触部位实施Z方向的位移约束,车架的约束和加载如图5所示。
经计算得到弯曲工况的von mises应力云图如图6所示,应力较大区域主要集中在前后端加载处,中间段纵梁和横梁应力很小。牵引座安装板处的应力最大为 316.599 MPa(图7所示),变形主要出现在前横梁端部,最大变形为14.1 mm,应变云图如图8所示。
2.2.2 扭转工况计算
扭转工况时左前轮悬空,其它约束和载荷处理同弯曲工况。经计算得到扭转工况下车架的应力和应变云图如图9和图10所示,与弯曲工况类似,较大应力也出现在车架前后加载处,最大应力值为 320.642 MPa,最大变形出现在前横梁加载两端为30.244 mm。
2.3 结果分析

▲图5 车架的加载和约束示意图

▲图3 车架有限元模型
▲图4 车架局部网格放大图

▲图6 弯曲工况车架应力云图

▲图7 弯曲工况牵引座处应力云图

▲图8 弯曲工况车架应变云图
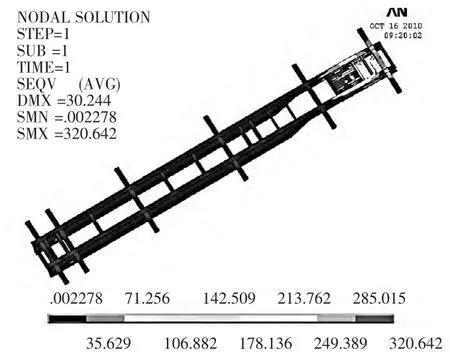
▲图9 扭转工况车架应力云图
通过静态分析发现,车架在弯曲和扭转两种工况下的应力值和应变主要发生在前后端加载处。两种工况下的最大应力为 320.642 MPa,小于材料的许用应力,满足强度要求;扭转工况下车架前横梁的变形较大为30.244 mm,满足刚度要求。从整体来看,车架中间纵梁和横梁存在很大的强度裕量,给车架的轻量化设计提供了很大的空间。

▲图1 0 扭转工况车架应变云图
3 车架结构的优化设计
根据静力分析结果,车架中间纵梁存在很大的强度和刚度裕量,材料的承载能力没有得到充分的利用。因此,根据ANSYS所提供的优化方法及APDL语言所具有的较强参数化分析功能,对车架纵梁重新建模,以纵梁为优化设计对象,选取满足弯曲工况进行结构优化,以寻求更为合理的纵梁结构参数。
3.1 优化设计模型的建立
车架整体材料一致,要求质量最轻即体积最小,所以优化的目标为纵梁的体积。通过优化结构体积达到优化结构自重的目的,当完成结构分析后,结构体积可在后处理中通过建立单元体积表,然后通过单元总体积算出结构的总体积[8-10]。以体积最小为目标函数的结构优化问题用数学模型描述:

式中:X=[x1,x2,...,xn]T为影响体积的设计变量; 体积函数 f(x)为目标函数;hv(x)为等式约束函数;gv(x)为不等式约束函数,约束条件为应力约束、位移约束、局部稳定、频率约束和动响应约束等。
根据设计要求,选择各构件的截面尺寸和局部的布置尺寸作为设计的对象。通过前面的分析得知,车架设计时已经充分考虑车架前端牵引部分的结构和强度,而车架纵梁具有很大的优化空间,因此选取纵梁进行优化。车架纵梁为工字型梁,前端和后端高度不同,选取后端纵梁高度、前端纵梁高度、纵梁腹板厚度和上下翼板厚度为设计变量,取值见表1。通过改变这些尺寸来改变车架刚度的变化,使应力更加均匀,达到减重的目的。
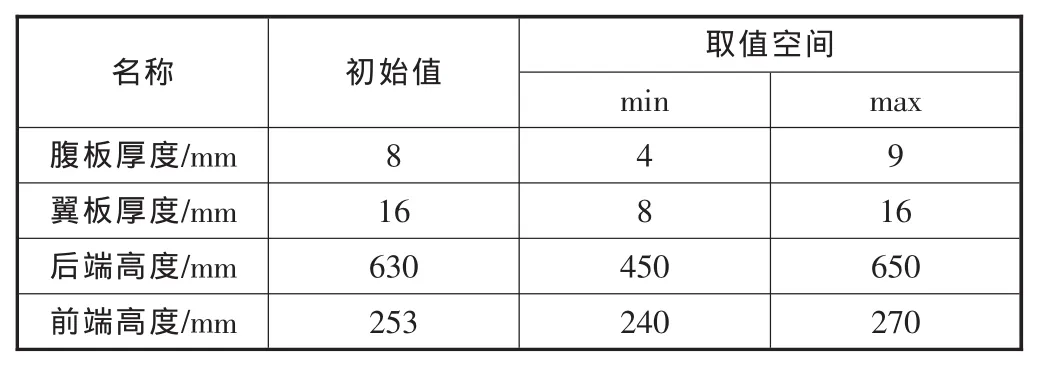
表1 设计变量参数表
3.2 优化设计结果分析
根据设计要求,约束函数可以是结构的应力或位移,也可以是结构的固有频率。为了得到尽可能符合实际需要,设计时必须选择合适的状态变量。本文在优化设计中,状态变量取材料的最大许用应力作为限制,构成优化设计中的约束,即性能约束。循环在第27次迭代达到最优解,优化前后纵梁各尺寸、最大应力和体积的变化见表2。
经计算校核,优化后的车架强度满足设计要求。经过优化设计后,体积由1.04×108mm3下降到0.82×108mm3,减小21.3%,车架质量约减小349 kg,优化后车架质量为3 019 kg。从表2可以看出,减小纵梁后端高度是车架减重的主要途径。
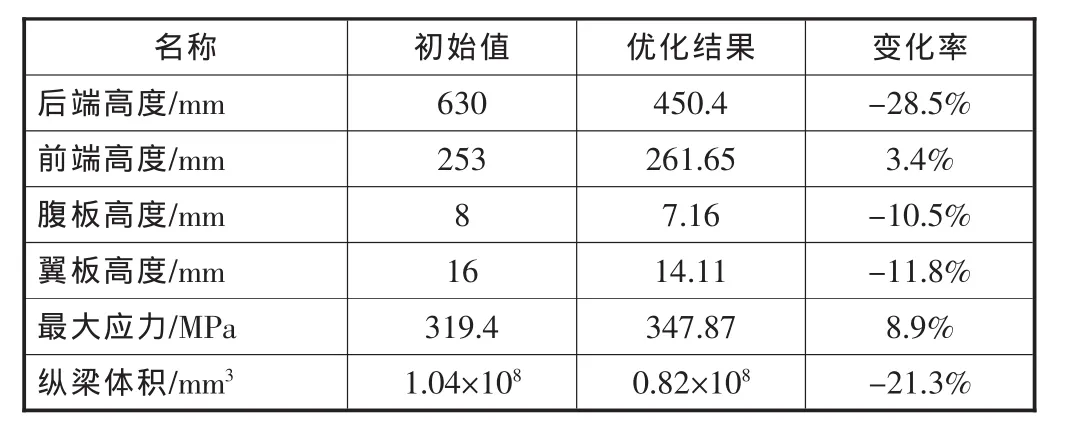
表2 优化前后车架总质量及变化率
4 结论
笔者运用有限元分析软件 ANSYS对车架进行了静力分析,车架应力较大部位发生在前后加载处,中间部位有很大的性能余量。为实现车架的轻量化,以纵梁为优化目标进行了结构优化设计,通过对纵梁高度和板厚进行尺寸优化,车架质量减轻了349 kg,大幅提高了气瓶运输车天然气的容积率,降低了气体运输成本,取得了良好的经济效益和社会效益,同时,也为其它车架的设计与改进提供理论参考和技术支持,具有重要的现实意义。
[1] 朱容庆.重型载重汽车车架轻量化设计研究[D].武汉:武汉理工大学,2006.
[2] 尹辉俊.重型自卸车车架的有限元分析及其早期断裂原因分析[D].武汉:华中科技大学,2006.
[3] 姜勇,顾洪枢,张文明.基于ADAMS的铰接式自卸车刚柔耦合动力学建模与仿真分析 [J].有色金属 (矿山部分),2014,66(3):64-67.
[4] 李正网.基于ANSYS的重型货车车架结构分析和优化研究[D].重庆:重庆交通大学,2009.
[5] 杨学军.SGA3722矿用汽车车架异常断裂的分析[D].北京:北京科技大学,2006.
[6] 张朝晖,王富耻,王鲁,等.ANSYS工程应用范例入门与提高[M].北京:清华大学出版社,2004.
[7] 谭继锦.汽车有限元法[M].北京:人民交通出版社,2005.
[8] 于国维.汽车起重机车架结构件参数化建模程序开发[D].长春:吉林大学,2008.
[9] 李峻,于学兵,张昆.汽车车架的优化设计方法[J].机械设计与研究,2005,34(2):39-41.
[10]冯国胜,刘玉杰,刘鹏.冶金专用车车架结构的优化设计[J].系统仿真学报,2006,18(2):537-539.

