平面连杆机构轨迹输出的小波分析
苍 鹏, 刘文瑞, 孙建伟
(长春工业大学 机电工程学院,吉林 长春 130012)
0 引 言
按给定设计要求,可将平面四杆机构多位置轨迹综合问题分为开区间给定设计要求轨迹综合问题和整周期给定设计要求轨迹综合问题两大类。基于数值图谱法的解题思想,傅里叶级数可以较好地实现整周期给定设计要求的平面四杆机构轨迹综合问题的求解[1-3]。但是由于傅里叶级数本身的缺陷(不能准确地描述非周期函数的特点),对于开区间给定设计要求的平面四杆机构轨迹综合问题的求解,无法保证设计区间的综合精度。
小波函数作为一个新兴理论,在短短的几十年里已经发展迅猛,其主要思想是从不同的频带提取函数的“平均”和“细节”特征,从而在描述平面四杆机构非整周期轨迹输出特点时具有傅里叶级数无法比拟的优势。因此它可以快速并精确的提取出开区间连杆轨迹的特点[4]。王成志[5]应用Haar小波多分辨率分析理论,实现了整周期连杆轨迹特征参数的提取。进而建立了相应的轨迹评价和轨迹复演模型,实现了整周期给定设计条件的平面四杆机构轨迹综合。Gloria[6]基于该理论也对尺度综合问题进行了研究[7]。吴鑫[8]提出了应用小波函数对平面四杆机构函数综合的方法,应用Mallat算法对给定函数进行小波变换,将经典尺寸型函数转换为小波特征参数,并应用模糊识别理论找出近似给定函数的尺寸型。文中通过对平面四杆机构开区间轨迹输出函数的小波分析,揭示具有相同基本尺寸型四杆机构小波特征参数之间的关系,为利用该关系实现开区间给定设计要求的连杆机构轨迹奠定理论基础[9]。
1 连杆曲线的小波特征参数描述
平面四杆机构模型如图1所示。
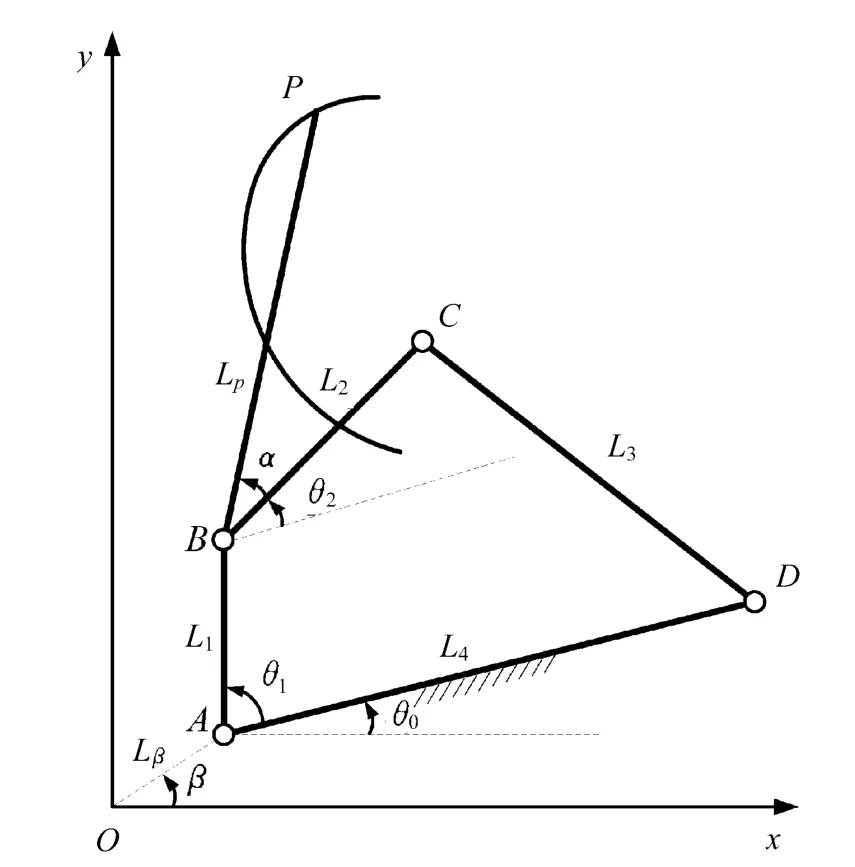
图1 平面四杆机构模型
其中O为坐标原点,AD为机架,AB、CD为连架杆,BC为连杆,P为连杆上任意一点,BP与BC的夹角为α,机架AD与x轴的夹角为θE,AO与x轴的夹角为β,杆AB、BC、CD、AD和BP所对应的杆长分别为L1、L2、L3、L4和LP,AO长度为Lβ,θ1为输入角,θ2为杆BC与AD的夹角。P点轨迹可以表示为复平面上的一组点的集合,机构处于一般位置时,可以用输入角θ1为自变量的函数表示:
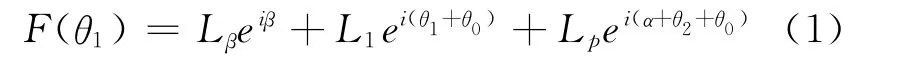
根据Haar小波理论对平面四杆机构输出轨迹进行离散化采样及预处理,采样点数为2j+1(j为小波分解级数),根据式(1),其中第m(m=0,1,…,2j)个采样点可以表示为:
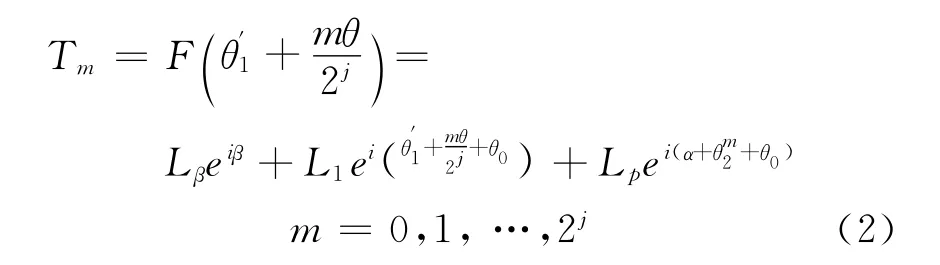
j——小波分解级数;
θ——设计区间;
通过对输出轨迹的离散化处理可以利用采样点描述平面四杆机构输出轨迹的特点,随着小波分解级数j的增加,采样点数也随之增加,对轨迹曲线的描述也更加精确。从式(2)可以看出,机构连杆曲线表达式包括机构参数Lβ,β,θ0,Lp和α。平面四杆机构轨迹输出函数的小波级数表达式可写为:
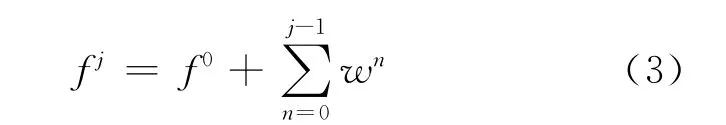
式中:f0——小波平均数;
wn——小波细节数。
f0和wn可由下式得到:
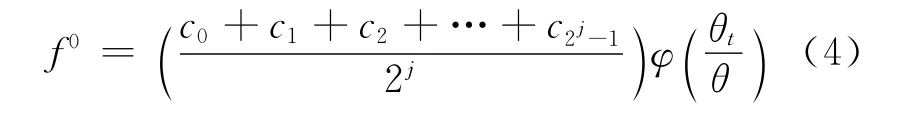
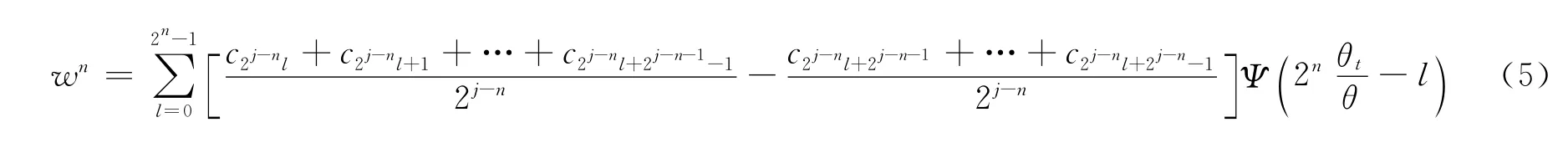
式中:θt——时间参数t的函数(θt=ωt,ω为输入曲柄的角速度);
φ——尺度函数;
Ψ——小波函数。
小波平均数和小波细节数定义为小波参数。
对式(5)进行无量纲标准化处理,即小波细节数的所有项除以小波细节数的第1项,得到:
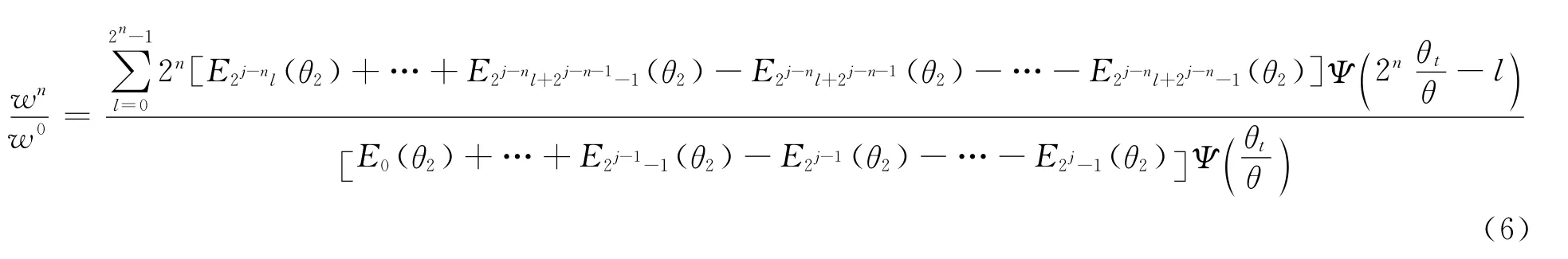
式中:
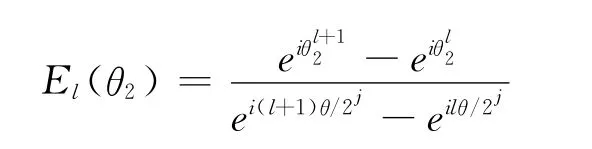
经过归一化处理后的小波细节数定义为小波特征参数[10]。通过对式(6)的分析可知,对于平面四杆机构的非正周期轨迹输出、机架旋转、P点位置和杆长的等比例缩放不影响预处理后的机构输出轨迹特征参数的Haar小波细节数。
2 验证算例
基本尺寸型相同的机构输出轨迹如图2所示。
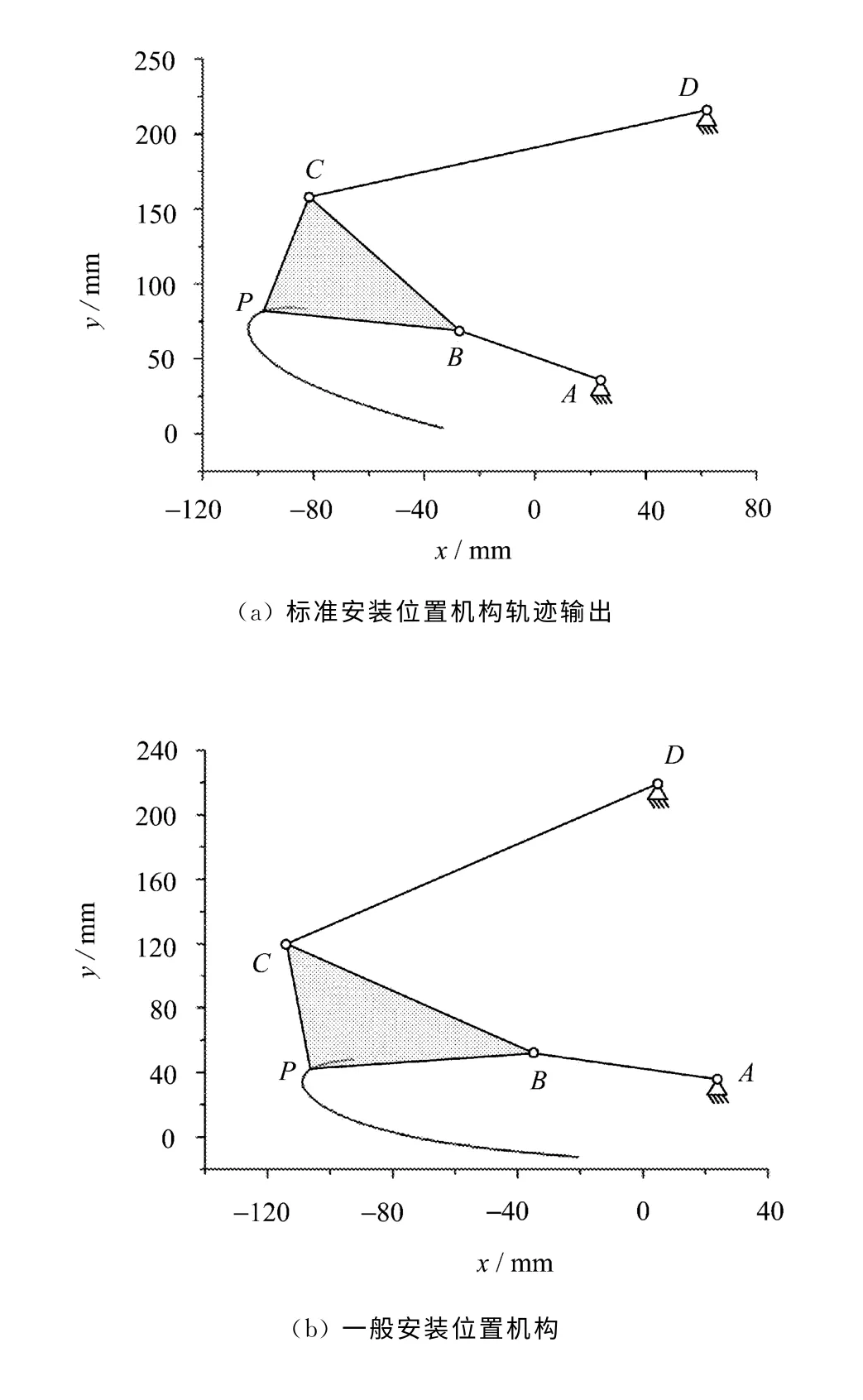
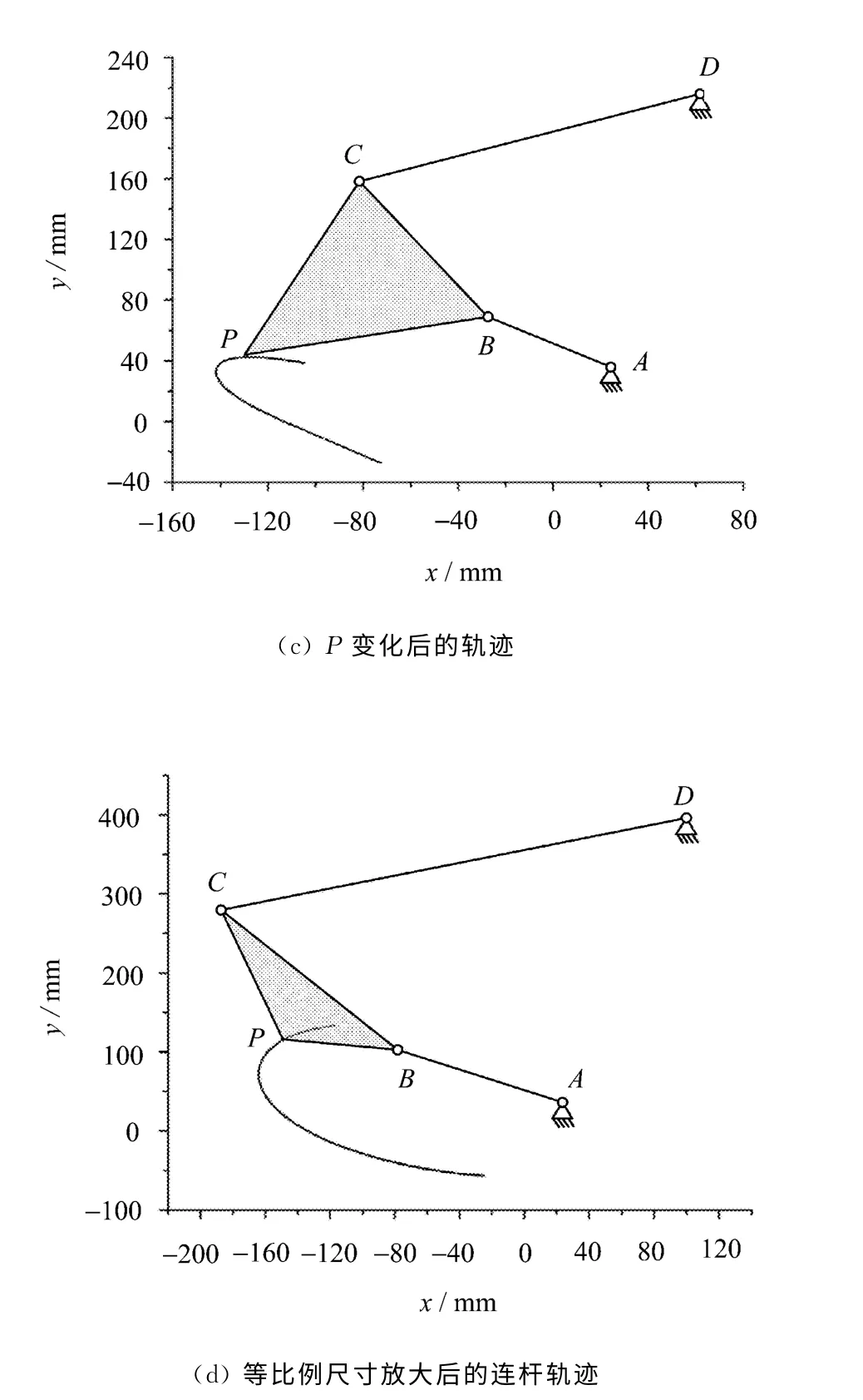
图2 基本尺寸型相同的机构输出轨迹
为验证上一节得到的结论,首先定义平面四杆机构的实际尺寸和安装参数为:L1=61mm、L2=104mm、L3=155mm、L4=184mm、LP=72mm、θ0=78°、α=48°、Lβ=43mm和β=56°。该机构的输出区间为θ1∈[47°,200°](机构输出连杆曲线见图2(a))。小波分解级数为j=5,此时机构输出连杆曲线对应的小波级数平均数和细节数见表1。接下来通过将机构安装位置旋转θ0=96°、连杆上任一点P的位置改变为LP=105mm和α=73°,将机构各杆长尺寸同时扩大为原机构尺寸的两倍,可以得到3组新的平面四杆机构。这3组机构的连杆轨迹曲线见图2(b)、(c)、(d)。
3组新机构输出连杆曲线对应的小波级数平均数和细节数见表1。

表1 基本尺寸型相同的不同机构小波特征参数
通过表1可以发现,虽然4组机构的尺寸不同,输出的连杆轨迹也不相同,但由于具有相同的基本尺寸型,所对应的机构输出小波特征参数完全相同(从而证明了第2节得出的结论)。
3 结 语
文中在复平面上建立了平面四杆机构轨迹输出的数学模型,通过预处理及小波变换对四杆机构输出轨迹进行分析,发现了同源四杆机构小波特征参数之间的关系。并通过算例对这一发现进行了验证。从算例的对比可以看出文中发现规律的正确性。该发现为利用小波级数理论进行平面四杆机构的开区间轨迹综合问题奠定了理论基础。
[1] Yu Hongying,Tang Dewei,Wang Zhixing.Study on a new computer path synthesis method of a fourbar linkage[J].Mechanism and Machine Theory,2007,42(4):383-392.
[2] G Mullineux.Atlas of spherical four-bar mechanisms[J].Mechanism and Machine Theory,2011,46(11):1811-1823.
[3] Chu jinkui,Sun jianwei.Numerical atlas method for path generation of spherical four-bar mechanism[J].Mechanism and Machine Theory,2010,45(6):867-879.
[4] Rodrigo Capobianco Guido.A note on a practical relationship between filter coefficients and scaling and wavelet functions of discrete wavelet transforms[J].Applied Mathematics Letters,2011,24(7):1257-1259.
[5] 王成志,纪跃波,孙道恒.小波分析在平面四杆机构轨迹综合中的应用研究[J].机械工程学报,2004,40(8):34-39.
[6] Gloria Galán-Marín,Francisco J.Alonso and José M.Del Castillo,Shape optimization for path synthesis of crank-rocker mechanisms using a waveletbased neural network[J].Mechanism and Machine Theory,2009,44(6):1132-1143.
[7] Mc Garva J,Mullineux G.Harmonic representation of closed curves[J].Applied Mathematical Modelling,1993,17(4):213-218.
[8] 吴鑫,褚金奎,曹惟庆.基于小波变换的平面四杆机构函数尺度综合研究[J].机械科学与技术,1998,17(5):704-706.
[9] 董小刚,秦喜文.信号消噪的小波处理方法及Matlab实现[J].长春工业大学学报:自然科学版,2003,24(2):1-3.
[10] 宋宇,王美玲,翟双.基于小波变换的图像压缩算示[J].长春工业大学学报:自然科学版,2011,32(6):558-561.

