习题教学中研究性学习的实践与思考

●卞国文 (扬中高级中学 江苏扬中 212200)



习题教学中研究性学习的实践与思考

●卞国文 (扬中高级中学 江苏扬中 212200)

我国一直倡导研究性学习，当前的状况是：有教材，无研讨；有课表，不上课；有口号，无行动；有理论，无实效.在应试教育的环境中，各种教辅资料铺天盖地，教师拼命地讲，学生拼命地做，题海战术，一轮又一轮，学生累，教师也累.如果讲一题，通一类；做一题，通一遍，从不同视角进行习题教学，追求解题方法的普适性，疲惫的师生也许能从“题海”中解放出来,也能引导学生将高中数学知识系统化、网络化，将知识连成线、织成网、铺成面，积累多种多样的解题策略，积累丰富的解题经验，从而提高学生的思维水平与综合能力.因此，我们应该在习题教学中开展研究性学习.下面介绍一次习题研究性学习的实例与同行交流.

此题是某市高三质量检测卷中的一道填空题，主要研究平面向量的数量积，这类问题是高中数学的重点和难点之一，也是高考的必考内容之一．学习和总结此类问题的解题原则、规律，对培养逻辑思维能力、提高数学素养都非常重要．学生学习中除了灵活应用基本原理和公式外，还必须讲究一些基本策略和方法，抓住问题的本质特征，采用合理恰当的方法来处理．对于这样的好题，如果学生仅作练习，教师仅作讲评，即使师生鼓掌赞叹“好题、妙题”，也不可能有多大意义和价值.因为我们仅停留在试题的欣赏层面，忽视了试题蕴藏的教育功能和学习功能.学习的主要目的在于提高数学解题能力和数学素养.

研究结果 经过2天后，有5个研究小组解答了此问题，给出以下5种解法.

视角1 平面向量的基本定理

则

因此

评析 利用平面向量基本定理进行转化是解决平面向量问题的通用方法，无需过多技巧，而许多学生在解题的过程中没有应用的意识.因此，教师在教与学的过程中应重视使用平面向量基本定理的思想方法的渗透．

解法2 算两次.

(1)

(2)

式(1)+式(2)×2,得

从而

因此

图1

解法3 几何法.

如图1所示，联结AC取点G使得AC=3AG,则

从而

评析 利用平面几何的简单知识，构造简单的相似比，显示了向量的代数和几何的双重身份.用有关平面几何的方法解决平面向量问题，既是对平面几何的深化和发展，又对“应用数学解决问题的数学观”形成有重要作用．

视角2 建系法

求解平面向量数量积第2种常见方法需要引入坐标，建立平面直角坐标系，是应对的常规方法.对于此类填空题，笔者利用特殊化思想，不妨设DA⊥AB，简化运算，效果甚佳．

解法4 特殊化思想建系法.

不妨令DA⊥AB，则以A为坐标原点、AB所在直线为x轴建立直角坐标系.设D(0,m),则

从而

又

故

评析 建系法是解决有图的向量问题的有效方法之一.笔者将∠DAB特殊化为直角，对于填空题(选择题)可以简化运算，在平时教学中适当的使用可以培养学生灵活的解题能力，若建系后设∠DAB=θ，也可以得到正确的结果，读者不妨一试．

视角3 投影法

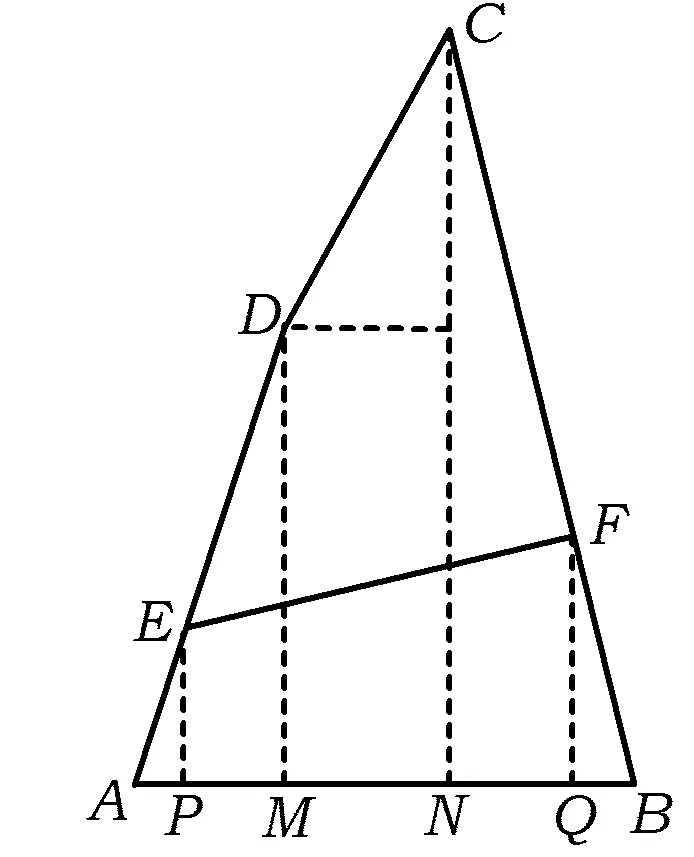
图2

解法5 相似法.

如图2所示，点C,D,E,F在AB上的投影分别为N,M,P,Q,则

MN=1.

由△FQB∽△CNB,得

从而

同理可得

因此

AB·PQ=7,

即

“茫茫题海，何处是岸”，广大数学教师都在苦苦思索，引导学生挣脱题海、摒弃题海战术、强化研究性学习是一剂良方.“数学就是需要对不同的思想进行研究”.在学习数学过程中，学习者所积累的知识、方法、经验经过加工、融合，会得出具有长久保存价值的或基本的典型结构与重要类型——模式.若能将其有意识地记忆固化，形成固有的模型和通法，当遇到一个新题目时，只需辨认它属于哪一类基本模式，联想此模式的通法，在记忆贮存中提取相应的方法加以解决，就能举一反三，以简驭繁，融会贯通.

因此，真正用好这些优质题，进行多角度开展研究性学习，从知识层面上看，既能完善学生的知识网络，又能增强学生处理问题的策略选择；从教学层面上看，既能引导学生多角度思考问题，又能调动学生学习的积极性；从思维层面上看，既能优化学生的认知结构，又能提升学生的思维品质，最终达到提高课堂实效性的目的.

[1] 张乃贵．一道难题的思考过程[J]．数学通讯：上半月，2013(11/12)：65．

[2] 王春．浅析平面向量数量积问题的常用处理方法[J]．福建中学数学，2014(5)：44.

[3] 陈传熙．由形入数探本质 求简至美归本真——谈谈“平面向量的基本定理与坐标运算(第1课时)”的教学设计[J]．数学通报，2014(4):19.