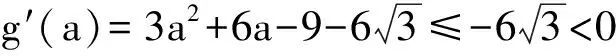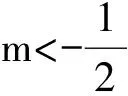必要条件论解题 稳扎稳打见功底
诸杰锋 (杭州市第九中学 浙江杭州 310020)
必要条件论解题 稳扎稳打见功底
诸杰锋 (杭州市第九中学 浙江杭州 310020)
数学解题的过程,重要的是展示思考问题的思维过程,理解数学问题的本质,从表象中梳理出解决问题的关键,归结到底就是充要条件变形的演化过程.通过研究近几年的各地数学高考试卷,发现一些试题都能通过转换思考角度,运用必要条件简洁明快地解决问题.下面以这些试题为例,阐述必要条件在解题中的应用.
1 善用必要条件求参数值
例1 设a∈R,若x>0时均有
[(a-1)x-1](x2-ax-1)≥0,
则a=______.
(2012年浙江省数学高考理科试题第17题)
解 当x>0时,不等式
[(a-1)x-1](x2-ax-1)≥0
恒成立的必要条件是当x=2时成立,即
[2(a-1)-1](22-2a-1)≥0,
得
(2a-3)2≤0.
又(2a-3)2≥0,故
(2a-3)2=0,
从而
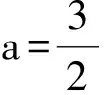
评注 本例若按常规思路,令
f(x)=[(a-1)x-1](x2-ax-1),
把问题看作f(x)≥0在(0,+∞)上恒成立,然后用导数知识去讨论求解,也可以求解,但过程繁杂,甚至有些学生做不下去,半途而废.而利用必要条件则可避免“小题大做”,其解法简洁明快,实在是精彩巧妙.
例2 设a,b∈R,若x≥0时恒有0≤x4-x3+ax+b≤(x2-1)2,则ab等于______.
(2013年浙江省数学高考文科试题第16题)
解 当x≥0时,不等式
0≤x4-x3+ax+b≤(x2-1)2
恒成立的必要条件是当x=1成立,即
0≤a+b≤0,
故
a+b=0,
于是x4-x3+ax+b=x4-x3+ax-a=
(x-1)(x3+a)≥0.
当0 综上可得a=-1,从而b=1,ab=-1. 评注 本例充分运用必要条件“两边夹”得到a+b=0,这是求解本题关键的一步. 例3 已知集合M={(a,b)|a≤-1,且b≤m},其中m∈R.若对任意(a,b)∈M,均有a·2b-b-3a≥0,求实数m的取值范围. 解 对于任意(a,b)∈M,不等式a·2b-b-3a≥0恒成立的必要条件是当a=-1,b=m时成立,即 -1·2m-m-3·(-1)≥0, 亦即 2m+m-3≤0. 令f(m)=2m+m-3,则f(m)在R上单调递增,且f(1)=0,得m≤1.当m=1时,2b+b-3≤0,故对任意a≤-1,b≤1,都有 a·2b-b-3a≥a·2b-3-3a= (a+1)(2b-3)≥0 成立.因此所求实数m的取值范围为m≤1. 评注 试题以“集合”的形式出现,简洁新颖,其实质是对任意的a≤-1,且b≤m,不等式a·2b-b-3a≥0恒成立,常规解法是采用“主元法”,但需分类讨论,解题过程实在繁琐.若先运用题设的必要条件得到参数m的范围,再结合题意对m=1的情形作充分性验证,其过程要简洁得多,思路也比较新颖. 例4 设函数f(x)=a2lnx-x2+ax,其中a>0. 1)求f(x)的单调区间; 2)求所有实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立. 注:e为自然对数的底数. (2011年浙江省数学高考文科试题第21题) 解 1)f(x)的增区间为(0,a),减区间为(a,+∞). 2)对x∈[1,e],不等式e-1≤f(x)≤e2恒成立的必要条件是 f(1)=a-1≥e-1, 即a≥e.由第1)小题知f(x)在[1,e]内单调递增,要使e-1≤f(x)≤e2对x∈[1,e]恒成立,只要 解得a=e. 评注 本例第2)小题的常规思路是分0 即可迅速获得问题的结果a=e,再作充分性验证,达到简捷求解,实现“大题小做”的效果. 评注 在不等价变形中,放缩的关键在于恰当.“放缩得太大或不够”,都会让解题过程陷入死胡同.尤其在一些数学竞赛中,缩放的关键点是一个很小的区间,如何修正放缩的结果是很关键的.“放缩得过了就回一点点”,“放缩得不够就要将力度扩大”,适当修正公式,选择合适的公式或定理. 证明 (2n)2>(2n)2-1=(2n-1)(2n+1), 故 随着食品行业的发展,功能性食品的研究与开发已经成为食品领域的前沿和热点,为了更好地学习“功能性食品”,将学习的知识点应用到实际生活中去,要对课程的教学内容进行重组,围绕学生在毕业后在食品、保健品行业从事功能性食品辅助开发、生产、检测、销售等工作所需要的综合能力和职业素养进行教学项目的选取,实时了解行业、企业的发展动态,对课程的教学内容进行实时更新,保证教学内容与岗位要求的一致性[3]。课程组及时修改教学计划,使课程教学项目紧跟行业发展和企业需要。 (1) 即 代入式(1)得 评注 本题的关键在于把根式或其他式子换成2个相邻的根式差,然后利用求和来消去中间部分,只剩2头.数学思想中的转化与化归,要求学生能够正确处理等价变形与不等价变形,以期达到完美的解题要求.转化与化归,最重要的是找到合适的构造结论. 1)求f(x)的单调区间. 解 1)当a=-1时,f(x)的递增区间为(-∞,+∞),无递减区间; 当a>-1时,f(x)的递增区间为(-∞,-1)和(a,+∞),递减区间为(-1,a); 当a<-1时,f(x)的递增区间为(-∞,a)和(-1,+∞),递减区间为(a,-1). 从而 -2≤f(1)-f(0)≤2, 即 解得 即 解 由题意得 从而 解得 故a=1.再结合-1≤f(0)≤1,-1≤f(1)≤1可得b=1,经验证,实数对(a,b)=(1,1)符合题意. 例8 已知函数f(x)=x3+(m+2)x2+(2m+1)x(其中m≠R).设函数f(x)除0外还有2个不同的零点x1,x2(其中x1x2≠0,且x1 解 由f(x)=x3+(m+2)x2+(2m+1)x=0得 x=0或x2+(m+2)x+2m+1=0. Δ=(m+2)2-4(2m+1)>0, 即 由f′(x)=3x2+2(m+2)x+(2m+1)=0,得 1)当m>4时,由 x1+x2=-(m+2)<0,x1x2=2m+1>0 知x1<0,x2<0,且 x1 8m-36, 化简得 (m+8)(2m-11)2>0, 从而 m>-8, 故 以上几例难度较大,而善用必要条件解题,则可化难为易,化繁为简,避免“小题大做”,甚至实现“大题小做”.因此有意识地善用必要条件解题,能缩小目标范围,打开解题思路,优化解题策略,提升思维品质.但是利用必要条件解题所得结果的严谨性往往有待于探究,因此要对所得结果作进一步的检验或证明.在平时我们只能作适当地变化和拓展训练,开阔视野,培养动态思维,锻炼数学思想,积累解题经验,提高应变能力,创造性地使用所学知识,才能从容地善用必要条件解题. [1] 郭志祥.“正”“误”例析“充分、必要条件”在解题中的应用[J].中学数学,2013(7):93-95. [2] 余锦银.高中数学审题策略[J].数学教学研究,2009(3):27-31.2 善用必要条件求参数范围
3 善用必要条件妙证不等式题


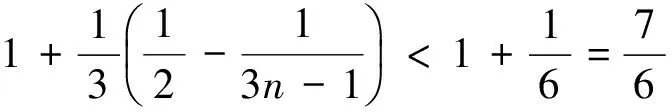
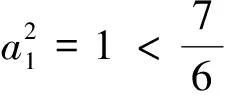






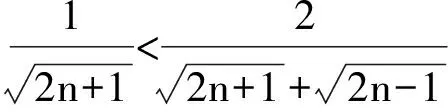



4 善用必要条件探求存在性问题