转子共频相关故障源源数估计与子带盲分离*

李纪永， 李舜酩， 田国成, 陈晓红

(1.南京航空航天大学能源与动力学院 南京，210016) (2.山东中实易通集团有限公司 济南,250000)(3.南京航空航天大学理学院 南京，210016)



转子共频相关故障源源数估计与子带盲分离*

李纪永1， 李舜酩1， 田国成2, 陈晓红3

(1.南京航空航天大学能源与动力学院 南京，210016) (2.山东中实易通集团有限公司 济南,250000)(3.南京航空航天大学理学院 南京，210016)

针对转子异常振动产生含交叉频率的响应，其共频相关故障源不满足统计独立要求，提出利用非负矩阵法在频域中计算故障源个数，不计及源信号和混合系统特性，可以正确估计出故障源数目或源数上限。提出利用小波包分解故障信号，选择互信息较小的子带进行重构，剔除共频信号并进行盲分离，得到独立非相关的源信号，保留了故障信息。理论及实验结果证明了所提出方法的有效性。

相关源； 非负矩阵分解； 互信息； 子带分解； 盲源分离

引言

航空发动机在研制和生产试车中经常出现异常振动现象，非相关源及存在交叉频率的相关源振动信号混合在一起，不满足源信号统计独立性条件[1-3]。传统的源数估计方法无法正确识别源信号数目，而基于标准独立量分析方法无法正确分离出此类信号[4-5]。文献[6]利用功率谱密度方法估计相关源数，在理论上估计出上下界，但不能确定具体数目。文献[4]指出利用高通滤波器过滤相关信号，然后利用独立量分析分离。基于高通滤波后的信号往往比原信号更独立这一特点，在实际应用中并不理想，指出自适应滤波方法需要源信号的先验概率分布。

笔者利用非负矩阵分解 (non-negative matrix factorization，简称NMF)方法[7]分解观测信号的功率谱密度系数，进而估计相关源数。非负矩阵对源信号无统计性要求，其纯加性的和对稀疏性的描述特性使得描述数据更加清晰。利用子带盲分离算法[1](sub-band decomposition independent component analysis,简称SDICA)对观测信号分离，得到观测信号子带，计算子带互信息[8](mutual information,简称MI)，剔除互信息最大的子带进行信号重构。该算法鲁棒性强，是分离相关源振动的有效方法。

1 基于非负矩阵分解的相关振动源源数估计

NMF数学表达形式为

Vm×n≈Wm×rHr×n

(1)

其中：V,W及H均为非负矩阵。

以V及W×H的欧几里德距离平方(square of eculidian distance,简称SED)为目标函数，约束条件为H的每一列归一化，表达式为

(2)

文献[7]提出了乘性迭代规则，证明其单调下降收敛特性。迭代规则为

(3)

式(1)形式上与盲信号分离线性瞬时混合模型相似，其表达式为

x(t)m×n=Am×ps(t)p×n

(4)

其中：x(t)为观测信号；s(t)为源信号；A为混合矩阵。

实际上所观测振动信号不满足非负条件，故将其进行傅里叶变换，得到

x(w)m×q=Am×rs(w)r×q=Am×rBr×ps(w)p×q

(5)

令Am×p=Am×rBr×p，Br×p为幅值系数矩阵。由于V,A及B均为正矩阵，满足非负矩阵分解条件。利用乘性迭代规则单调下降收敛特性，求解源信号与降维信号欧式距离首先降为0时的r即为源数。

2 相关振动源盲分离

含有同频的各观测信号是相关的[9]，基于独立分量分析的盲分离技术不能直接将相关信号分离，笔者利用小波包分解，将相关的子频带信号即共频信号剔除，重构后进行基于独立量分析的盲分离，即可得到分离信号。

源信号x(t)的第i个源信号si(t)可以表示为

si(t)=si,1(t)+si,2(t)+si,3(t)+…+si,L(t)

(6)

其中：si,1(t),si,2(t),si,3(t),…,si,L(t)为源信号si(t)的各个子带分量。

信号通过多分辨率小波包分解，相当于通过一个迭代的带通滤波器Ti[10-11]。源信号矩阵信号s经过这个滤波器得到子带分量为

si(t)=Ti[s(t)]

(7)

子带盲分离的数学模型为

xi(t)=Ti[As(t)]=ATi[s(t)]=Asi(t)

(8)

由式(8)可知，混合矩阵通过滤波器未发生变化，观测信号子带分量是混合矩阵与源信号子带分量的乘积，可利用观测信号子带盲分离进行相关源分析。利用互信息值大小表征子带信号之间的相关性。当互信息为1时，子带信号完全相关；互信息为0时，子带信号不相关。为编程方便，利用高阶累积量表达互信息值，表达式为

(9)

选取互信息较小的子带重构信号，利用快速独立量分析[12]进行盲分离，即可得到剔除同频分量的故障源信号。

3 相关信号盲分离数值仿真

构造一组相关振动信号

(10)

其中：s0为s1，s2，s3，s4的共频信号。

图1为未添加共频信号时信号波形。首先对观测信号进行源数识别，当传感器数目大于源数时(这里设源数为4，传感器数为5)，其混合矩阵A1为对系数矩阵进行非负矩阵分解，得到源数与目标函数关系如图2，3所示。当传感器数目大于源数时，可正确估计信号源数；当传感器数目小于源数时，可估计信号源数的下限。

图1 仿真信号时间历程Fig.1 Simulation signal time sierious

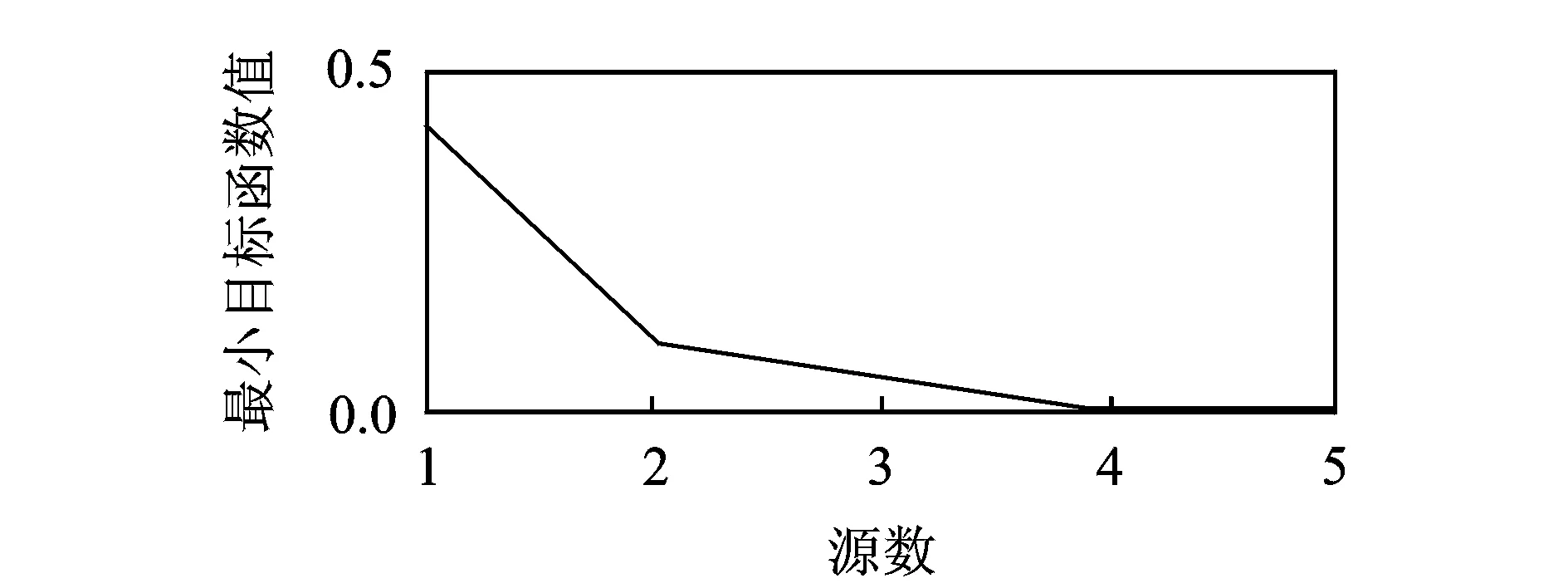
图2 超定情况下最小目标函数值Fig.2 Min objective function value in over-determination case

图3 欠定情况下源数与最小目标函数值Fig.3 Min objective function value in under-determination case

随机生成一个混合矩阵，对源信号进行混合，利用FastICA方法分离，恢复出的源信号如图4所示，其Amari差值计算为0.218 2[8]。由y1的频谱可以看出共频信号依然存在，并未分出，分离失败。

图4 FastICA恢复信号时间历程与频谱图Fig.4 FastICA recovery signal time series and frequency spectrum

利用小波包子带分解，分解层数为1时相当于采用高通滤波器提取其高频信号进行盲分离，其Amari差值计算为0.11，亦未分离出共频信号，采用5层小波包子带分解，计算各层子带间互信息值，提出互信息最大的子带对信号进行重构，然后进行盲分离，恢复信号及其频谱图如图5所示。可以看出，共频信号被分离出来，计算出的Amari差值为0.001 8，较好地分离出了共频信号，并保留了原始信号特征信息。

4 转子相关故障信号盲分离实验

在单转子实验台测取4 kr/min时基础松动-碰摩-偏心耦合故障，实验装置如图6所示。对测得的信号进行去均值并进行相关降噪处理，利用非负矩阵法计算源数，计算得源数为3，如图7所示。

图5 子带分解恢复信号时间历程与频谱图Fig.5 Sub-band decomposition blind source separation time series and frequency spectrum

图6 转子实验台Fig.6 Rotor test rig

图7 实验信号源数与最小目标函数Fig.7 Experimental signal source number and min objective function value

利用自相关方法对观测的故障信号进行降噪，然后直接进行盲源分离，所得频谱如图8所示。各路信号同频成分多，主要包括50，250，500 Hz等，说明各传感器测得的源信号相关性强，利用相关方法信号降噪并对降噪后的信号进行小波包子带分解，分解层数为6，计算其互信息值，选取适当阈值去除同频分子带分量，然后对不相关的子带进行重构，经过盲源分离所得的频谱结果如图9所示。可明显看出，信号噪声降低，频率成分简洁，s1信号工频显著，为不平衡故障，s2信号倍频成分丰富，噪声成分小，可判断为碰摩故障，s3信号倍频成分丰富, 但噪声较多，可认为由基础松动振动不断冲击底座造成。此方向信号较强，四倍频被剔除掉，说明各源信号存在4倍频，以上推测符合碰摩故障特征。

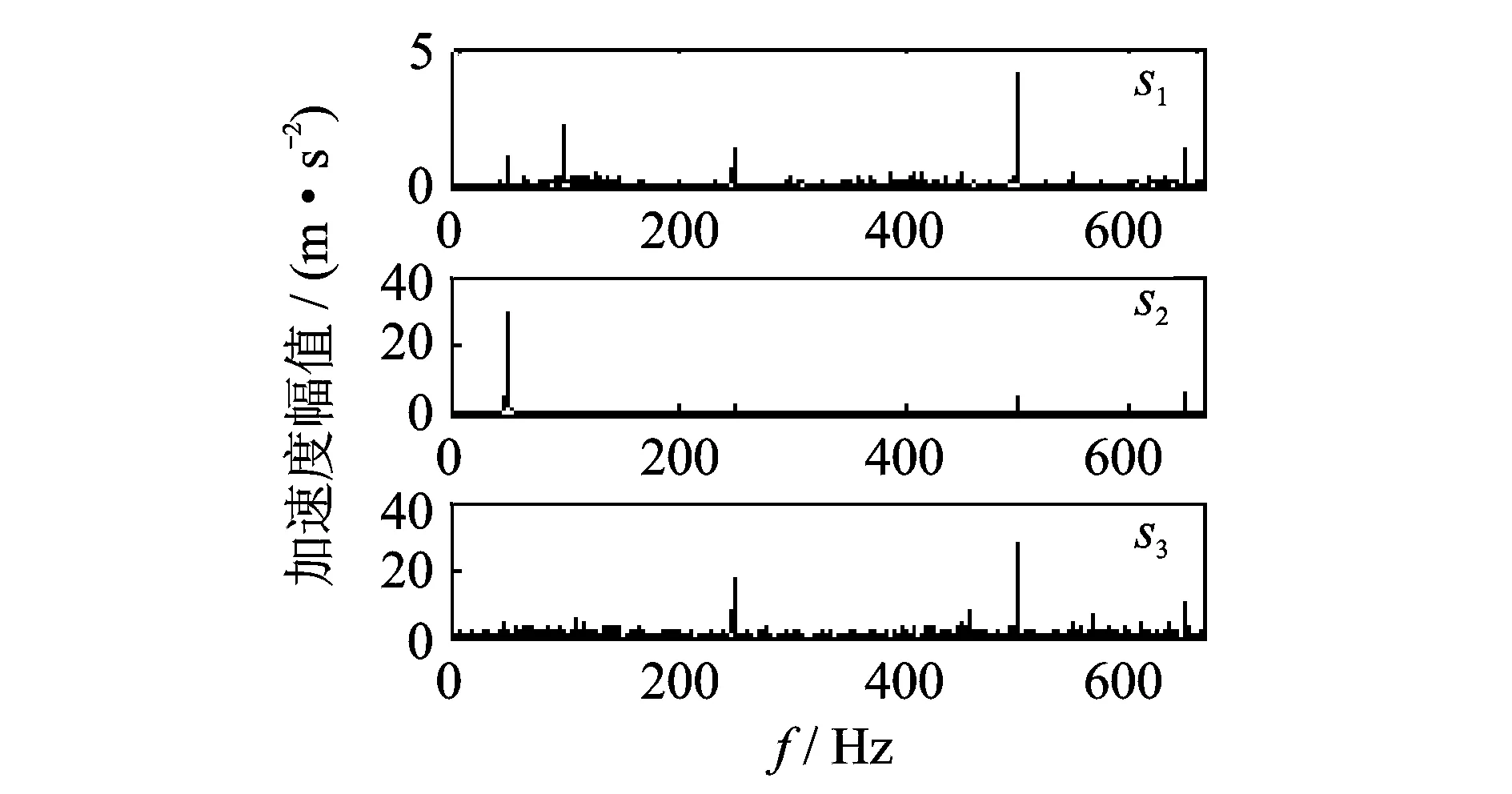
图8 降噪故障信号盲分离源信号频谱Fig.8 Denoising fault signal blind source separation spectrum

图9 实验信号子带盲分离频谱Fig.9 Experimental signal sub-band decomposition blind source separation spectrum

5 结 论

1) 利用非负矩阵乘性迭代规则收敛特性进行故障信号降噪并在频域进行分解，无需考虑源信号及混合系统特性，寻找代价函数最小值即可求得源的个数。当传感器数大于源数时，可正确估计出源数，当传感器数目小于源数时，可估计其下限。

2) 利用相关小波包子带分解故障信号，计算其互信息，选取阈值剔除同频相关信号，进行信号重构后，保留了故障信号的信息。

3) 对重构后的信号进行盲分离，提取出不相关的信号，与直接进行盲分离的结果进行对比，更易于诊断故障及分析因果关系，从而得出系统振动源故障特性。

[1] 周晓峰,杨世锡,甘春标.相关机械振源的盲源分离方法[J].振动与冲击,2012,31(14):60-64.

Zhou Xiaofeng, Yang Shixi, Gan Chunbiao. Blind source separation of statistically correlated sources[J]. Journal of Vibration and Shock, 2012,31(14):60-64. (in Chinese)

[2] 杜建建,李舜酩,张袁元,等.平板叶片的相关激励响应实验[J].实验室研究与探索,2011,30(1):14-17.

Du Jianjian, Li Shunming, Zhang Yuanyuan, et al. Research on stimulus-response test of flat blade[J]. Research and Exploration in Laboratory, 2011,30(1):14-17. (in Chinese)

[3] 陈茉莉，李舜酩，温卫东,等.多源拍振分析方法与实验[J].振动、测试与诊断,2011,31(2):202-206.

Chen Moli, Li Shunming, Wen Weidong, et al. Analysis and experiment on multi-source beat vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(2):202-206. (in Chinese)

[4] Ivica K, Damir S. Wavelet packets approach to blind separation of statistically dependent sources[J]. Neuro Computing, 2008,7(1):1642-1655.

[5] Araki S, Makino S, Aichner R, et al. Subband-based blind separation for convolutive mixtures of speech[J]. Trans Funament, 2005,2(88):3593-3603.

[6] 李宁.频率域盲信号分离理论研究[D].武汉:华中科技大学，2007.

[7] Lee D D, Seung H S. Alg or ithms for non-negative matrix factorization advances in neural information processing[J]. Advances in Neural Information Processing Systems, 2001,13:556-562.

[8] Li Y, Cichocki A, Amari S. Analysis of sparse representation and blind source separation[J]. Neural Computation, 2004,16(6):1193-1234.

[9] 杨世锡,焦卫东,吴昭同.应用JADE盲分离算法分离统计相关源[J].振动工程学报，2003,16(4):498-501.

Yang Shixi, Jiao Weidong, Wu Zhaotong. Application of JADE to separation of statistically correlated sources[J]. Journal of Vibration Engineering, 2003,16(4):498-501. (in Chinese)

[10]Mallat S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1989,11(7):674-693.

[11]Graps A. An introduction to wavelets[J]. Computational Science & Engineering, 1995,2(2):50-61.

[12]Erkki O, Yuan Zhijian. The fast ICA algorithm revisited: convergence analyis[J]. Neural Networks, 2006,17(6):1370-1381.

*航空自然科学基金资助项目(2012ZD52054)；国家自然科学基金资助项目(61403193)；南航基本科研业务费科研资助项目(NS2014081)

2013-01-28；

2013-03-18

10.16450/j.cnki.issn.1004-6801.2015.01.025

TH132.4

李纪永，男，1985年1月生，博士研究生。主要研究方向为旋转机械故障信号处理。 E-mail：ljynav@163.com