工作模态控制解耦的塔形直线超声电机*

陈乾伟， 鞠全勇， 黄卫清， 时运来

(1.金陵科技学院机电工程学院 南京，211169)(2.南京航空航天大学机械结构力学与控制国家重点实验室 南京，210016)



工作模态控制解耦的塔形直线超声电机*

陈乾伟1， 鞠全勇1， 黄卫清2， 时运来2

(1.金陵科技学院机电工程学院 南京，211169)(2.南京航空航天大学机械结构力学与控制国家重点实验室 南京，210016)

针对现有塔形超声电机无法相互独立控制法向和切向振动等实际应用问题，提出了一种工作模态控制解耦的塔形直线超声电机。塔形电机设计有两个非共面的正交工作模态，分别为用于独立控制法向振动的x-z面内对称振动模态以及用于独立控制切向振动的y-z面内弯振模态。相应设计了压电陶瓷片的极化布置方案，即塔形电机的压电陶瓷片分为A，B两相，其中A相用于激励x-z面内对称振动模态，B相用于激励y-z面内弯振模态。通过对电机A，B两相相互独立控制就可以实现两个非共面正交工作模态的控制解耦。实验表明，在解耦控制条件下，当A相电压固定为400 Vp-p，B相电压在0～400 Vp-p变化时，电机运行速度与B相电压成正比，最大运行速度为420 mm/s，最小运行速度为23 mm/s。

工作模态； 控制解耦； 超声电机； 压电

引言

直线超声电机(linear ultrasonic motor，简称LUSM)是利用压电陶瓷元件的逆压电效应激发出定子的超声振动，并利用定子和动子之间的摩擦作用，把定子的微幅振动转化成动子宏观直线运动的作动器。它具有低速大力矩、断电自锁、无电磁干扰、定位和速度控制精度高等优点，在精密驱动和特殊环境等领域有着广泛的应用[1-5]。

目前，应用于精密驱动等领域的直线超声电机原理多样、形式各异，但大多数电机是两正交工作模态驱动的驻波型电机，其中基于面内工作模态的超声电机成为了研究热点。例如：文献[6]研制的“shaking beam”直线超声电机；Kurosawa等[7]研制的V形直线超声电机；姚志远等[8]研制的双变幅杆直线超声电机；金家楣等[9]研制的方尖塔形超声电机以及时运来等[10]研制的蝶形直线超声电机。以上5种超声电机具有以下优点。

1) 电机的两个正交工作模态分别为共面的对称和反对称振动模态。由于共面的对称和反对称振动模态为近型模态，因此采用这两个正交工作模态的超声电机具有较好的频率一致性。

2) 电机定子具有相似的结构。定子含有若干个(≥2)在空间均布的压电振子，这些均布的压电振子之间相互平行或具有一定的夹角，压电振子在端部被连接为一体并形成驱动足。笔者将这种拓扑结构称为“塔形”结构。该结构具有“聚焦”能量的优点，能够有效地将振动能传递到定子的驱动足。

正是因为上述5种超声电机都具有优良的性能，已经产业化并有许多实际应用[6-10]。但是，共面的对称和反对称振动模态在电机的输出性能控制方面存在不足。这是因为共面的对称振动模态用于提供驱动足端面质点的法向振动，共面的反对称振动模态用于提供驱动足端面质点的切向振动，两者动态合成驱动足端面质点的椭圆运动轨迹。在超声电机运行过程中，构成椭圆运动轨迹的法向和切向振动对电机输出性能的贡献是不同的。法向振动的作用：a.通过改变定动子之间的动态压力进而控制定动子之间的摩擦力；b.使定动子周期性的接触和脱离，从而将定子端面质点的微观振动转换为动子正向或反向的宏观运动。切向振动用于驱动负载，输出功率。可见，实现驱动端面质点椭圆运动轨迹的法向和切向振动相互独立地控制，对于超声电机输出性能的控制具有重要意义[11]。

由于现有“塔形”结构超声电机的工作模态均为共面的对称和反对称振动模态，这两种模态在控制上是相互耦合的，无法实现法向和切向振动相互独立地控制。针对此问题，笔者提出了一种工作模态控制解耦的含“塔形”结构定子的直线超声电机。

1 电机设计

1.1 塔形定子设计

图1为笔者设计的塔形定子结构示意图。塔形定子含有两个正方形截面的柱形结构，这两个柱形结构在端部被锥形的驱动足联接，两个柱形结构的外表面黏贴有压电陶瓷片。

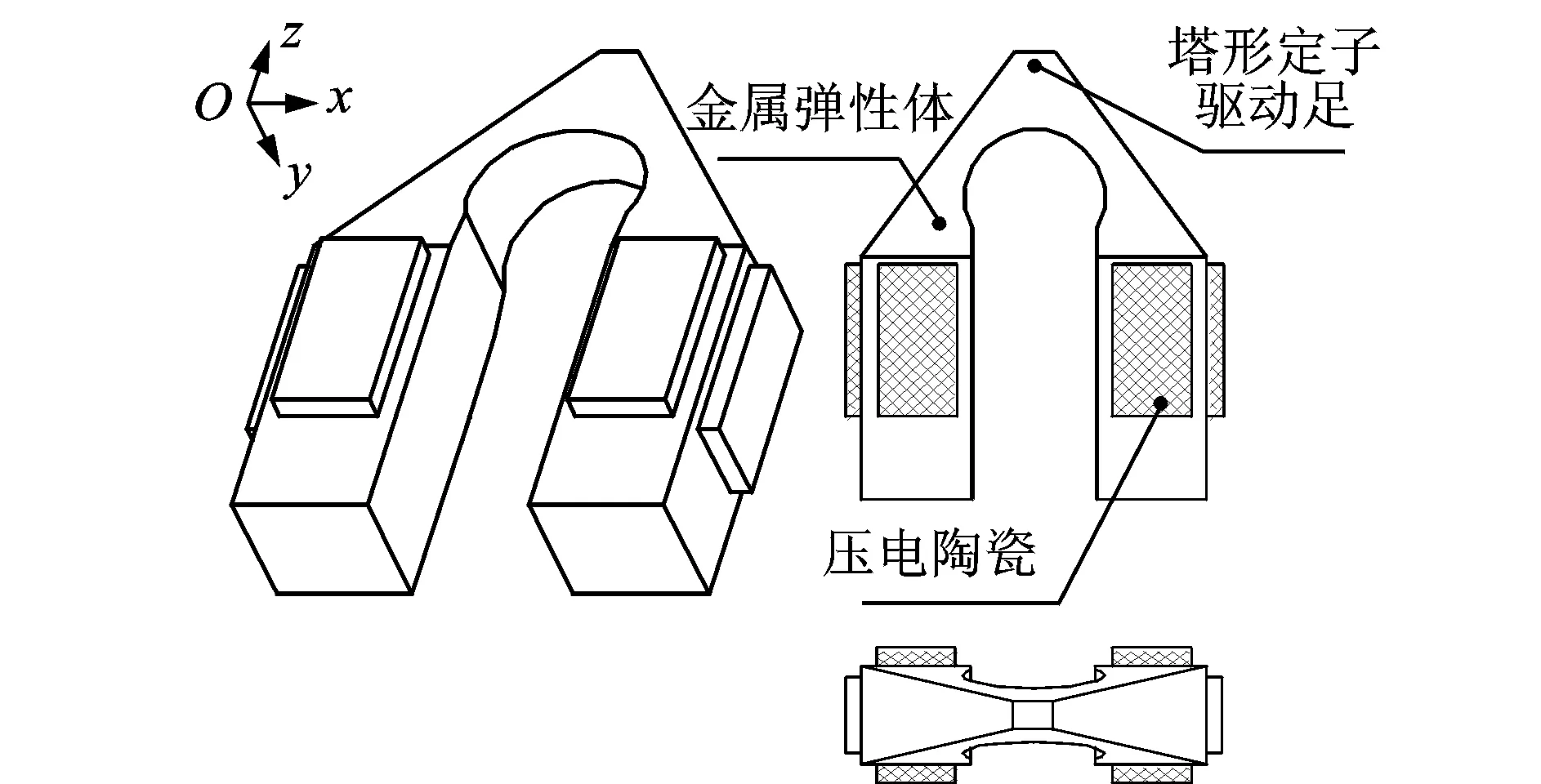
图1 塔形定子结构示意图Fig.1 Schematic diagram of the tower-type stator′s structure

为了保证定子的两个正交工作模态控制解耦，选择如图2所示的两个非共面的正交模态作为塔形定子的工作模态：一个是具有局部弯振模态的x-z面内对称振动模态；另一个是y-z面内2阶弯振模态。在这两个模态下，定子端部的振动不同：当以x-z面内对称振动模态振动时，定子端部仅产生z方向的法向振动，如图2(a)所示。当以y-z面内2阶弯振模态振动时，定子端部仅产生y方向的切向振动，如图2 (b)所示。由于x-z面内对称振动模态的激振力Fxz位于x-z面内，y-z面内弯振模态的激振力Fyz位于y-z面内，而x-z平面和y-z平面是正交的，即激振力Fxz在y-z面的投影为0(激振力Fyz在x-z面的投影为0)，所以上述两个模态可以相互独立地控制，进而可以对定子的法向振动和切向振动进行相互独立地控制。

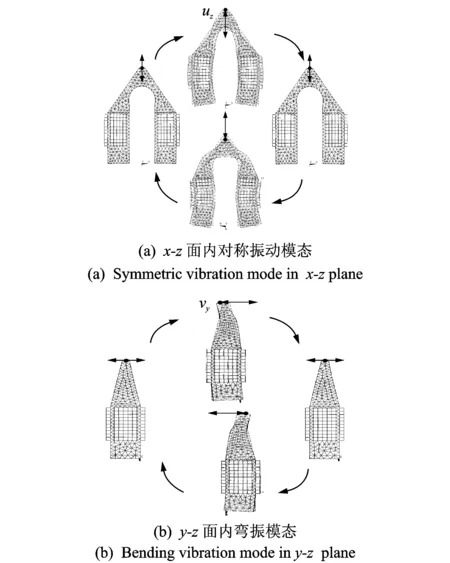
图2 塔形定子的工作模态Fig.2 The tower-type stator′s operating mode

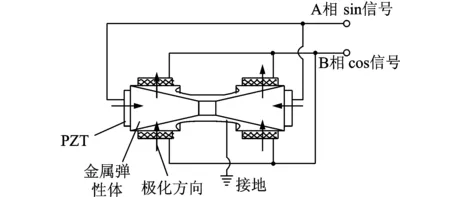
图3 压电陶瓷片的极化布置方案图Fig.3 Scheme of PZT′s polarization and arrangement

图3为压电陶瓷片的极化布置方案。整个塔形超声电机定子共用6片压电陶瓷，沿厚度方向极化，其中2片压电陶瓷构成A相，用于激励塔形定子产生x-z面内对称振动模态；另外4片压电陶瓷构成B相，用于激励塔形定子产生y-z面内弯振模态。这样就可以通过对电机A，B两相相互独立控制来实现两个正交模态的控制解耦。

当定子的两个工作模态具有一致的频率时，在相位差为φ的两相同频电压信号的激励下，其驱动足表面质点的运动可表示为

(1)

其中：z方向的法向振动uz由A相信号单独激励；y方向的切向振动vy由B相信号单独激励，两者在控制上是解耦的；U，V为位移响应幅值；φ为相位差。

从式(1)中消去时间t，则有

(2)

当两相同频电压信号的相位差φ=π/2时，其质点的运动轨迹方程为

(3)

由式(3)可以看出，此时驱动足表面质点的运动轨迹为一规则椭圆。根据上述设计方案制作的塔形定子样机如图4所示。塔形定子尺寸为20 mm×6 mm×30 mm，质量为20 g。

图4 塔形定子样机Fig.4 The prototype of the tower-type stator

1.2 电机整体结构设计

塔形定子制作好之后，还需要完成以下工作才能构成塔形超声电机：设计并制作相应的动子；将定子与动子安装在共同的基座上；选择合适的预压力使定子与动子相互接触。这些工作就是电机的整体结构设计，整体结构设计的合理与否将严重影响到电机的运行稳定性和定位精度。

由于一般采用购买的商品导轨或平台作为直线超声电机的动子，因此在电机整体结构设计中主要考虑2个问题：定子与动子的安装；定子与动子之间预压力的施加。在参考Nanomotion电机整体结构[12]的基础上，设计了如图5所示的塔形定子驱动的基于三滚子结构的一维运动平台，其行程为30 mm。

图5 塔形定子驱动的一维运动平台Fig.5 The one-dimensional moving platform driven by the tower-type stator

该结构主要由3个滚子(轴承)、滑板、铰链、基座、预压力加载机构、塔形定子及一维运动平台构成。由于采用了三滚子结构，再加上侧向的螺栓和蝶簧的作用，在消除定子安装侧隙的同时，使得定子安装夹持的切向位移刚度远大于法向位移刚度，有利于作动器的稳定运行和精密定位[13]。

2 实 验

2.1 模态实验

采用德国Polytec公司生产的PSV300F-B型高频扫描激光测振系统对塔形定子进行模态实验。实验结果如图6和表1所示。图6中,vA为速度振幅。理论计算值与实验结果对比如表2所示。从实验结果可知：a. 在设计的工作频率附近, 存在2个近频的正交模态，其振型与设计所选择的2个工作模态的振型 (如图2所示)一致，并且在80VP-P电压定频激励下，测得x-z面内对称振动模态下驱动足端面z方向的法向振幅为0.8 μm，y-z面内弯振模态下驱动足端面y方向的切向振幅为5 μm；b.图6(a)和图6 (c)所示的幅频曲线只有一个峰值，没有出现两个近频的峰值，说明塔形定子的两个工作模态在控制上是相互解耦的。

图6 激光多普勒测振仪实测的定子工作模态频率及振型Fig.6 Operating modal′s frequency and vibration types

表1 塔形定子模态实验结果

表2 塔形定子的ANSYS计算结果与模态实验结果对比

Tab.2 Comparation between stator′s theoretical results and modal testing results

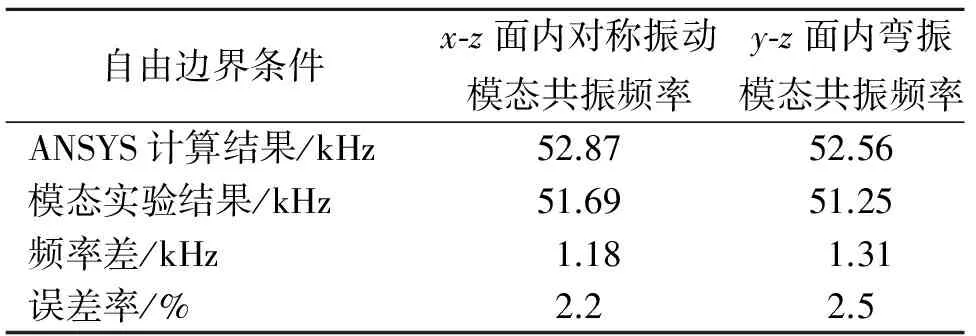
自由边界条件x⁃z面内对称振动模态共振频率y⁃z面内弯振模态共振频率ANSYS计算结果/kHz52．8752．56模态实验结果/kHz51．6951．25频率差/kHz1．181．31误差率/%2．22．5

2.2 机械特性实验

塔形超声电机驱动信号平台由信号发生器和两个功率放大器构成。实验时，信号发生器发出具有一定相位差的两路同频正弦电压信号，经功率放大器放大后，输出驱动电机。

图7为塔形超声电机测试系统，它主要由图5所示的一维运动平台和Renishaw XL-80激光干涉仪两部分构成，用来测试塔形超声电机驱动运动平台的性能指标。Renishaw XL-80激光干涉仪的测量范围0～80 m，分辨率为1 nm，最大测量速度为4 m/s，最高采样频率为50 kHz。测试实验在10万等级洁净房环境中进行。

图7 塔形超声电机测试系统Fig.7 The testing system of the tower-type USM

图8为塔形超声电机A，B两相相互独立控制的机械特性曲线。可以看出：a. 当A相驱动电压固定不变时，电机速度与B相驱动电压有较好的线性关系, 当B相驱动电压固定不变时，电机速度与A相驱动电压有较强的非线性关系, 这说明法向和切向振动模态对电机速度的影响是不同的，其中切向振动模态直接影响电机速度；b. 当A, B两相采用相同的激励电压时，塔形电机的A, B两相的死区电压为150 Vp-p, 当B相的激励电压固定为400 Vp-p，则A相的死区电压保持150 Vp-p不变；当A相的激励电压固定为400 Vp-p，则B相的死区电压降为40 Vp-p, 这说明法向振动模态的激励电压越大，则切向振动模态的死区电压越小，而切向振动模态的激励电压对法向振动模态的死区电压影响较小；c. 驱动电压为0～400 Vp-p时, A, B两相驱动电压为400 Vp-p，电机具有最大运行速度为420 mm/s；A相驱动电压为400 Vp-p、B相驱动电压为50 Vp-p，电机具有最小运行速度为23 mm/s；这说明切向振动模态的死区电压越小，电机稳定运行的最低速度越小，则预期的定位精度越高。

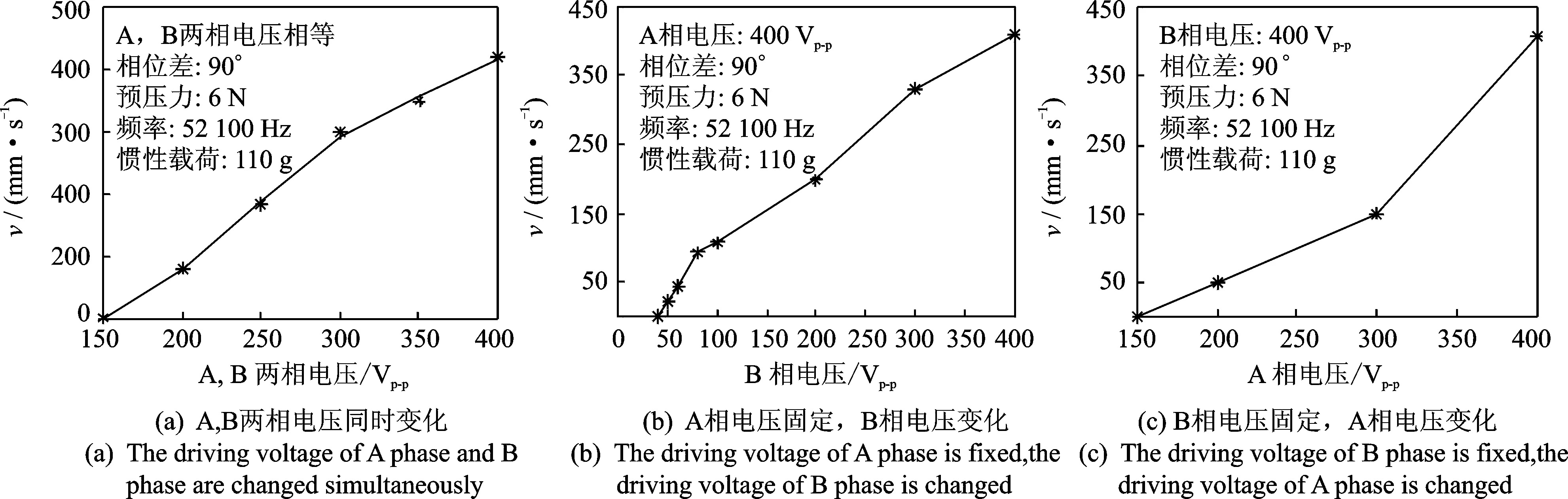
图8 塔型超声电机解耦控制的机械特性曲线Fig.8 Mechanical characteristic curve of the tower-type USM under the mode-control-decoupling condition

3 结 论

1) 提出并研制了一种工作模态控制解耦的塔形直线超声电机。该电机两个非共面的正交工作模态为x-z面内对称振动模态和y-z面内弯振模态。x-z面内对称振动模态由A相信号单独激励，用来激发定子驱动足的法向振动；y-z面内弯振模态由B相信号单独激励，用来激发定子驱动足的切向振动。通过对电机A，B两相相互独立控制来实现2个正交模态的控制解耦。

2) 在解耦控制下，法向振动模态的激励电压越大，则切向振动模态的死区电压越小，电机稳定运行的最低速度越小，预期的定位精度越高。

3) 经测试，在解耦控制的条件下，A相电压固定为400 Vp-p，B相电压在0～400 Vp-p变化时，电机运行速度与B相电压成正比，最大运行速度为420 mm/s，最小运行速度为23 mm/s。

[1] Zhao Chunsheng．Ultrasonic motors technologies and applications [M]. Beijing : Science Press and Springer-Verlag Berlin Heidelberg, 2011:1-19．

[2] 陈乾伟，黄卫清，赵淳生．超声电机寿命测试的方法研究[J]．振动、测试与诊断，2004，24(1)：19-22．

Chen Qianwei, Huang Weiqing，Zhao Chunsheng. Measurement of service life of ultrasonic motors(USM) [J]．Journal of Vibration，Measurement & Diagnosis，2004，24(1)：19-22．(in Chinese)

[3] 陈乾伟，时运来，黄卫清．新型塔形直线超声电机[J]．中国电机工程学报，2010，36(30)：27-32．

Chen Qianwei，Shi Yunlai，Huang Weiqing．A novel tower-shaped linear ultrasonic motor[J]．Proceedings of the CSEE，2010，36(30)：27-32．(in Chinese)

[4] 陈乾伟，黄卫清．斜动子与塔形定子构成的单驱双动超声电机[J]．振动、测试与诊断，2012，32(1)：28-33．

Chen Qianwei，Huang Weiqing. A single-phase-drive bi-directional moving ultrasonic motor composed of an inclined slider and a tower-type stator[J]．Journal of Vibration, Measurement & Diagnosis, 2012, 32(1): 28-33．(in Chinese)

[5] 陈乾伟，黄卫清．塔形超声电机的突变结构弹性支撑[J]．振动与冲击，2012，31(24)：74-81．

Chen Qianwei, Huang Weiqing. The tower-shaped ultrasonic motor(USM)′s elastic support with abrupt changing configuration[J]. Journal of Vibration and Shock, 2012,31(24):74-81．(in Chinese)

[6] Yoon S，Kim H，Choi J,et al. Linear piezoelectric ultrasonic motor：U.S.Patent，6984920[P]. 2006-01-10.

[7] Kurosawa M, Kodaira O, Tsuchitoi Y, et al. Transducer for high speed and large thrust ultrasonic linear motor using two sandwich-type vibrators[J]. IEEE Transactions on Ultrasonic Ferroelectrics and Frequency Control, 1998,45(5): 1186-1195．

[8] 姚志远，杨东，赵淳生．杆结构直线超声电机的结构设计和功率流分析[J]. 中国电机工程学报, 2009, 29(24)：56-60．

Yao Zhiyuan，Yang Dong，Zhao Chunsheng. Structure design and power flow analysis of bar-structure linear ultrasonic motors[J]．Proceedings of the CSEE, 2009, 29(24): 56-60．(in Chinese)

[9] 金家楣，张建辉，赵淳生. 新型方尖塔形定子二自由度超声电机的结构设计、驱动机理与性能研究[J]．振动与冲击，2009，28(12)：63-67．

Jin Jiamei，Zhang Jianhui，Zhao Chunsheng．Research on construction, principle, and performances of a novel two-degrees of freedom ultrasonic motor with an obelisk stator[J]．Journal of Vibration and Shock，2009，28(12)：63-67．(in Chinese)

[10]时运来，赵淳生. 蝶形直线超声电机优化设计[J]．振动、测试与诊断，2012，32(6)：1-10．

Shi Yunlai, Zhao Chunsheng. Application of response surface methodology for optimization of butterfly-shaped linear ultrasonic motor[J]. Journal of Vibration，Measurement & Diagnosis, 2012，32(6)：1-10．(in Chinese)

[11] Ueha S，Tomikawa Y. Ultrasonic motors theory and applications[M]. Oxford : Oxford University Press，1993：160-190．

[12] Waldbronn W W. Piezoelectric drive,especially a holding frame，a friction element and a circuit configuration：U.S. Patent，6979934B1[P]. 2005-12-27．

[13] 于会民，王寅，陈乾伟，等．三滚子结构夹持的直线型超声电机[J]．机械科学与技术，2012，31(2)：250-254．

Yu Huimin，Wang Yin，Chen Qianwei，et al. A linear ultrasonic motor clamped with three-roller clamping scheme[J]. Mechanical Science and Technology for Aerospace Engineering，2012，31(2)：250-254．(in Chinese)

*国家自然科学基金资助项目(51375224，51275235)；金陵科技学院青年教师科研基金资助项目(Jit-b-201318)

2014-04-24；

2014-05-11

10.16450/j.cnki.issn.1004-6801.2015.01.017

TM356； TB55; TH138

陈乾伟, 男，1972年5月生，博士、讲师。主要研究方向为直线超声电机及其应用技术。曾发表《斜动子与塔形定子构成的单驱双动超声电机》(《振动、测试与诊断》2012年第32卷第1期)等论文。 E-mail：chenqw@jit.edu.cn