复杂系统参数不确定度的传递特征与理论建模*

唐冰松, 韩晓林, 杨绘峰

(1.大连理工大学工业装备结构分析国家重点实验室 大连，116024)(2.东南大学江苏省工程力学分析重点实验室 南京，210096)(3.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)



复杂系统参数不确定度的传递特征与理论建模*

唐冰松1, 韩晓林2, 杨绘峰3

(1.大连理工大学工业装备结构分析国家重点实验室 大连，116024)(2.东南大学江苏省工程力学分析重点实验室 南京，210096)(3.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

对不确定度进行推广，发展了多参数广义不确定度的概念，并对广义不确定度的基本性质进行分析。对复杂系统参数广义不确定度的传递特征进行研究并对传递特征进行分类，研究了单一子系统不确定度的传递模式和特征，传递矩阵中元素的绝对值对目标参数不确定度的计算结果有着重要影响。分析了各个子系统参数不确定度传递过程中的主要和次要作用并建立相应的判别准则。算例表明了该理论模型在研究复杂系统参数不确定度传递问题时的有效性和可行性。

复杂系统； 不确定度； 传递矩阵； 传递模式

引言

近年来，参数不确定度的传递问题逐渐成为热点，然而对该领域的研究目前还处于起步阶段。Attivissimo等[1]采用实验的方法针对系统误差对全局不确定度的影响展开了研究。Mauris等[2]对不确定度采用模糊方法进行定义，采用此法研究不确定度的传递问题具有特别的优势，得出了不错的结果。文献[3-6]探讨了不确定度研究存在的问题、影响因素、主要计算方法及稳定性等。Mari[7]对一个动力引擎进行计算，研究了参数不确定度在传递过程中的主要特征并对结果进行了验证。Zhang等[8]对圆参数在极坐标的条件下建立了随机误差传递模型。王金星等[9]提出一种现行轮廓滤波器的不确定度传递规律的计算方法，可以由输入轮廓的不确定度计算出经过滤波后的输出不确定度。以上成果大体是基于具体的工程项目对某一特定参数进行不确定度研究，但面对复杂系统中的参数不确定度的计算时，采用以上文献方法进行计算时并不能很好地解决，因此需要发展针对复杂系统参数不确定度的理论模型。

笔者在研究复杂系统误差传递的基础上，对不确定度的定义进行拓展。发展了多参数广义不确定度的概念，对广义不确定度的性质进行分析和讨论，对复杂系统参数不确定度的传递特征进行研究。进一步分析了单一子系统不确定度的传递模式和特征，给出各个子系统参数不确定度主次作用的计算与判别准则。

1 广义不确定度的定义及性质

倪育才[10]对单个参数不确定度的定义为

u(xi)=sqrt(∑(xik-xi0)2/(n-1))

(1)

其中：u(xi)为第i个观测指标的标准不确定度；xik为第i个观测指标第k次观测结果；xi0为观测结果的平均值。

目前，广泛采用的是单个参数的不确定度，但单个参数的不确定度在评定某些工业产品时不太合适，需要发展多参数不确定度评定某些特定的产品。广义不确定度概念的提出将不确定度的参数扩充到n维，极大地拓展了不确定度问题的应用领域。设X=(x1,x2,…,xn)，X为含有n个待观测参数的n向量。令

(2)

其中：G(x1,x2,…,xn)表示含有n个参数的不确定度的区间函数。

若n=1，G(x1)表示参数x1的不确定度的区间长度，属于一维区间长度；若n=2，G(x1,x2)为参数x1，x2不确定度范围函数，可表示为二维平面问题。

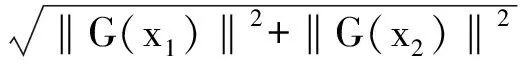
(3)

(4)

式(3)，(4)不确定度的边界如图1所示。图1中各半径可以表示为

图1 多参数广义不确定度范围边界Fig.1 The boundary of generalized uncertainty for multiple parameters

广义不确定度对描述多参数目标观测结果的漂移具有重要的意义。笔者提出的多参数广义不确定度式(3)，(4)是在各参数指标互相独立的基础上提出的。由图1可知，多参数广义不确定度范围的边界是包含了所有参数不确定度的一个封闭圆；但此定义的广义不确定范围存在一个盲区，即任何一次的观测结果都不会落入此盲区内。以双参数不确定度为例，图2将双参数不确定度观测目标出现的概率划分为若干区域。灰色区域为观测目标所涉及两个参数不可能出现的区域，为双参数的盲区；星号区域为观测目标所涉及双参数高概率出现区域，为高概率区域；空白区域为观测目标所涉及双参数低概率出现区域，为低概率区域。将参数扩大到n时，广义不确定度的边界包络线涵盖了所有参数可能出现的区域，同时含n个参数不确定度的包络线范围内包含较大的盲区。图2中关于高概率和低概率可能出现区域服从若干概率分布在相关的文献中已有大量成果，文献将特定的概率分布与不确定度联系起来，对不确定度范围的置信区间进行了研究。

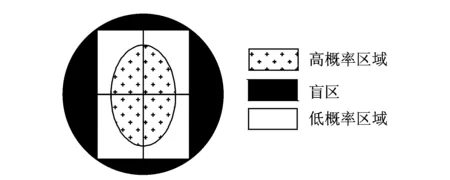
图2 双参数不确定度观测目标出现概率区域划分Fig.2 The different region divisions with different probable occurrences for double parameters

2 复杂系统参数不确定度传递特征

复杂系统一直是系统科学研究的重点，系统的组成方式不同，会影响到最终结果；因此在研究复杂系统问题时，需要定义各个系统的组成方式。笔者定义的复杂系统以最简单的多个子系统并联为例，研究各子系统的不确定度与上一层级系统的不确定度之间的关系，如图3所示。

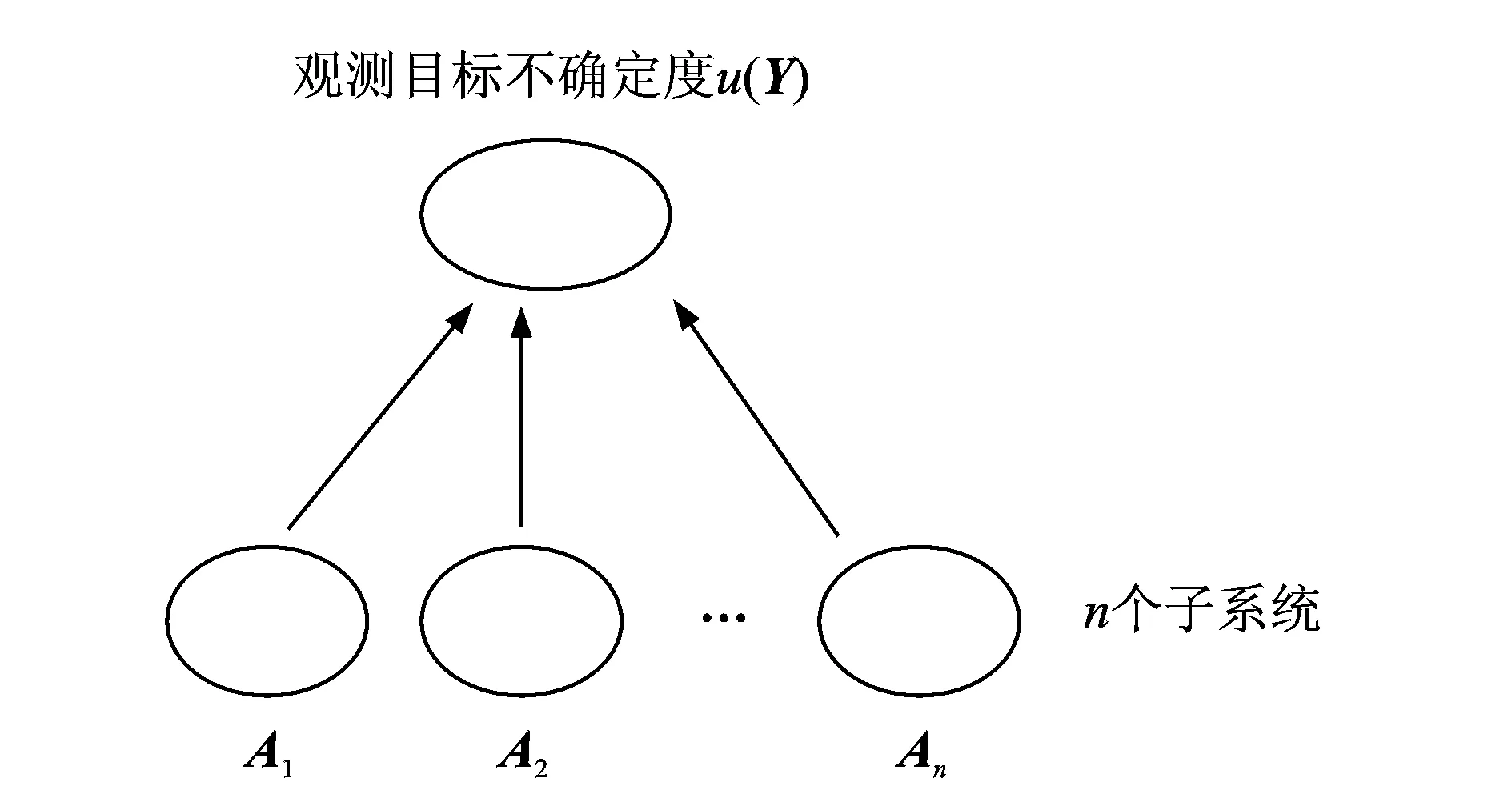
图3 观测目标与各子系统不确定度之间的传递关系Fig.3 The mechanism of parameter uncertainty propagation in the complex system

图3中的A1,A2,…,An为各个子系统参数不确定度的传递矩阵，为二阶矩阵。令u(Y)为上一层级参数的不确定度，u(X1),u(X2),…,u(Xn)为各个子系统观测目标参数的不确定度。各子系统观测参数的不确定度与上一层级参数的不确定度的传递关系为

(5)

若考虑各个子系统的传递矩阵互相耦合的效应，则式(5)改写为

(6)

式(6)中考虑了在传递过程中各个子系统之间耦合效应，耦合项为Aij,i≠j。为了研究的简便，假设在实际的传递过程中各子系统的传递函数没有耦合效应，则(5)式成立。考虑单个子系统观测参数的传递特征

u1(Y)=A1u(X1)

(7)

其中：u1(Y)表示单个子系统观测目标不确定度传递到上一层级参数的不确定度。

由式(4)可知

(8a)

(8b)

则

‖u1(Y)‖=‖A1u(X1)‖≤‖A1‖‖u(X1)‖

(9)

若传递矩阵的范数‖A1‖=χ，则式(9)改写为

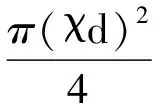
(10)

进一步

(11)

对式(11)进行讨论：

2) 若χ2>1，则传递函数矩阵对传递结果的作用是扩大的，上一层级中多参数不确定度的边界大于单个子系统中多参数不确定度的边界,扩大因子为χ2。

由式(5)可知，上一层级系统参数的不确定度是各个子系统观测目标不确定度经传递后叠加的结果，则

(12)

式(12)可以进一步改写为

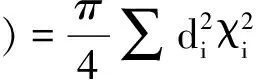
(13)

由式(13)可知，上一层级系统参数不确定度的边界大小由各个子系统的传递矩阵的范数(缩放因子)和多参数不确定度的边界范围共同决定。

3 单一子系统不确定度传递模式与特征

目标参数不确定度由各子系统观测目标参数的不确定度经传递矩阵传递叠加而成，叠加后参数的不确定度的边界为式(13)所示。由于单一子系统传递机制及对参数最终传递结果有着重要的意义，因此单一系统传递矩阵元素对传递结果的影响至关重要。考察某一子系统传递矩阵中的元素特征及其传递模式的分类对研究参数不确定度的问题有着重要意义。现研究单一子系统观测目标不确定度的传递过程

(14)

其中：u(x11),u(x12),…，u(x1n)为所有子系统观测目标不确定度分量；Y=(y1,y2,…,yn)T为上一层级系统参数不确定度向量。

2.3 指导学生制作个人简历，分享成功应聘技巧。高校辅导员作为过来人必然有一些制作个人简历及应聘的技巧，应毫无保留的与学生分享和探讨。如笔者就经常与学生探讨在互联网时代如何巧妙利用网络平台为就业服务。以通过电子邮件投递个人简历为例，首先，主题应在尽量简洁的情况下明确应聘者姓名、联系方式及应聘职位，便于招聘人员明确应聘者求职意向与其联系；其次，邮件投递时间应尽量靠近招聘截止日期，这个做法是为了使招聘人员在大量邮件中尽早接触到应聘者的邮件，在还未产生审阅疲劳前可了解到应聘者的信息。

(15)

在工业领域应用中，以式(15)为代表的观测目标参数互不耦合的情况普遍存在。由不确定度的定义可知，参数不确定度是以某一数值为中心，并在该数值两侧以一定概率分布的形式出现。因此不确定度是以该数值为对称轴的等间距区间。依据不确定度的特点，传递矩阵中对角线的元素正负不影响最终传递的结果，但和元素的绝对值有直接的关系。若|aii|≥1，u1(y1)的不确定度的区间范围伸长，伸长倍数为|aii|；若|aii|<1，u1(y1)的不确定度的区间范围收缩，收缩倍数为|aii|。因此式(15)可以改写为

(16)

式(16)与式(10)的关系为

(17)

式(17)给出了传递矩阵范数、对角元素与单一子系统观测目标不确定度之间的联系，表明在后者一定的情况下，传递矩阵范数和对角元素存在的对应关系。

单一子系统不确定度传递模式与特征主要侧重于传递矩阵中元素的特征对最终传递结果的影响，式(16)和式(17)表明不确定度的传递模式和特征与误差的传递模式与特征有着显著的区别。

4 子系统参数不确定度传递主次作用的度量

各个子系统观测目标不确定度在传递到上一层次系统参数不确定度过程中的重要性程度各不相同，为了区分各子系统观测目标不确定度传递过程中的相对“地位”，需要定义一个衡量参数不确定度传递主要和次要作用的参数。令

(18)

5 算 例

5.1 多参数广义不确定度

若存在一个互相独立的参数组x1,x2,…,xn，x1,x2,…,xn单个参数的不确定度可以表示为一个区间G(xn)∈[-rn,rn]，双参数的不确定度可以表示为G(xi,xj)∈[-rij,rij]，其中

(19)

以此类推，m参数的不确定度可以表示为G(xi,xj,…，xm)∈[-rim,rim]，其中

rim=

(i≠j≠…≠m)

(20)

多参数不确定范围边界如图4所示。

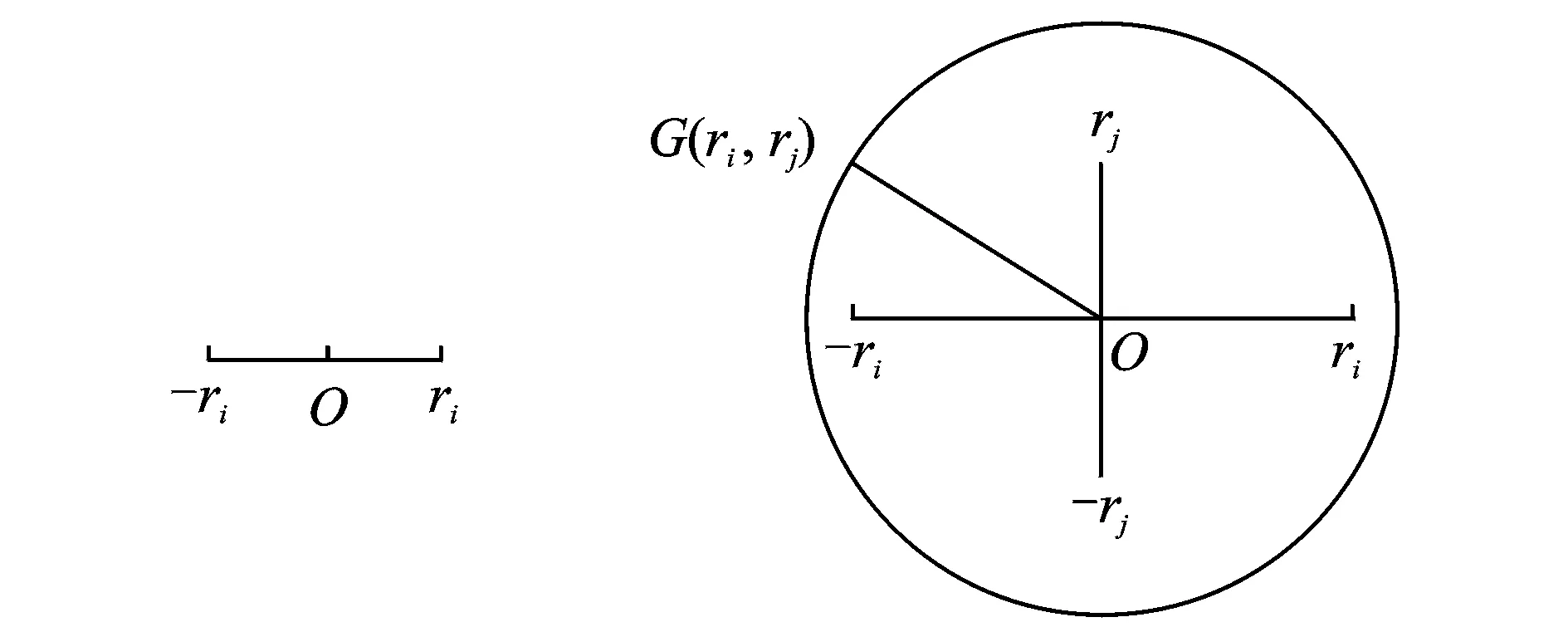
图4 单参数和双参数广义不确定度的范围和边界Fig.4 The boundary of generalized uncertainty for single and double parameters

5.2 复杂系统参数不确定度传递与主次作用度量

因不确定度是一个以真值为中心的区间，因此直接利用笔者提出的理论对不确定度进行计算存在一定的困难。为了计算的方便，记参数xn的不确定度G(xn)=[-rn,rn]=Rn，这里Rn特指不确定度半径rn的大小。若下一层级子系统的传递矩阵为

(21)

由A1，A2，A3矩阵可以求得矩阵范数‖A1‖2=2.288>1(扩大)；‖A2‖2=0.441<1(收缩)；‖A3‖2=5.734>1(扩大)。

因为不确定度是一个对称区间，根据式(16)可知，3个子系统的传递矩阵可以改写为

由式(10)计算可得

(22)

第1个子系统双参数广义不确定度传递结果边界上界所围成的面积范数为

(23a)

(23b)

第2个子系统双参数广义不确定度传递结果边界上界的面积范数为

(24a)

(24b)

第3个子系统双参数广义不确定度传递结果边界上界的面积范数为

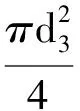
(25)

由式(12)，(22)～(24)可得

(26)

由式(13)可得

sup(‖u(Y)‖)=1 477.777

(27)

即双参数观测目标的不确定度可以表示为G(y1)=[-16.5,16.5]，G(y2)=[-12.3,12.3]，双参数不确定度上界边界的面积范数为1 477.777。

另外，由式(18) ，(22)，(23b)，(24b)可得到各个子系统的传递主次作用排序为3>1>2。

6 结束语

误差描述的是观测目标与真值之间的偏差，不确定度描述的是观测目标以一定概率在真值两侧偏移程度，两者是以两个不同的概念描述同一个事实。误差问题在理论上已有大量的成果，包括误差度量、分离和控制等[11]，但在实际应用上，误差问题还是没有彻底地解决。不确定度概念的引入为解决这类问题提供了一个更好的手段，不确定度不用区分系统误差和随机误差，以概率的形式给出观测目标出现的区间，在控制观测目标偏离真值的手段上更加灵活。因此在工业上逐渐摒弃了采用误差描述产品的精度的惯有手段，改用不确定度的方法描述产品的精度问题。

笔者根据复杂系统的特点提出了广义不确定度的概念，将不确定度的概念拓展到参数为n的情况，并对广义不确定度的主要性质进行了探讨。发展广义不确定度将进一步扩大不确定度概念的应用领域，使之成为描述产品精度问题除误差外又一个强又力的手段。在一些文献中已对不确定度有了大量的研究，得到了不少有意义的成果，但复杂系统参数的不确定度问题，特别是传递问题成果较少，应当引起重视。笔者对复杂系统参数不确定度(广义)的传递特征、单一子系统的传递模式与特征、子系统不确定度(广义)传递主次作用的度量等进行了深入地分析和探讨。所研究主题除了对系统整体(宏观)的传递机制进行详细分析外，对单一子系统(微观)的传递特征也进行了探讨，并对不确定度的外延进行了扩展，得到了一些有意义的结论，为推进研究复杂系统不确定度问题进一步发展做了一些有意的尝试。

[1] Attivissimo F, Cataldo A, Fabbiuno L, et al. Systematic errors and measurement uncertainty: An experimental approach[J]. Measurement, 2011,44:1781-1789.

[2] Mauris G, Lasserre V, Foulley L, et al. A fuzzy approach for the expression of uncertainty in measurement[J]. Measurement, 2001,29:165-177.

[3] Martens H. Evaluation of uncertainty in measurements-problems and tools[J]. Optics and Lasers in Engineering, 2002,38:185-306.

[4] Mayer V. Measurement Uncertainty[J]. Journal of Chromatography A, 2007,1158:15-24.

[5] Wallace J. Ten methods for calculating the uncertainty of measurement[J]. Science and Justice，2010,50:182-186.

[6] Magari R T. Uncertainty of measurement and error in stability studies[J]. Journal of Pharmaceutical and Biomedical Analysis, 2007,45:171-175.

[7] Mari L. A computational system for uncertainty propagation of mearsurement results[J]. Measurement, 2009,42:844-855.

[8] Zhang Defen, Maropoulos P G. Random uncertainty propagation in estimates of sphere parameters from coordinate measurements[J]. Machine Tools & Manufacture, 2006,46:1362-1368.

[9] 王金星,将向前.线性轮廓滤波器的不确定度传递规律的研究[J].计量学报,2005,26(4):313-316.

Wang Jinxing, Jiang Xiangqian. A study of uncertainty propagation based on linear profile filter[J]. Acta Metrological Sinica, 2005,26(4):313-316. (in Chinese)

[10]倪育才.实用测量不确定度评定[M].2版.北京：中国计量出版社,2007:61.

[11]刘明,章青.运动多体理论和神经网络的机床热误差补偿[J].振动、测试与诊断,2010,30(6):657-611.

Liu Ming, Zhang Qing. Thermal error model and compensation of machining tool using multibody system theory and neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(6):657-611. (in Chinese)

*国家自然科学基金资助项目(50608016)

2013-02-15；

2013-06-28

10.16450/j.cnki.issn.1004-6801.2015.01.014

TH701; TB92； O192

唐冰松，男，1982年5月生，博士生、工程师。主要研究方向为动态测试与诊断，桥梁健康监测。曾发表《一种基于结构动态特性的物理参数识别算法及应用》(《工程力学》2009年第26卷第6期)等论文。 E-mail:tangbingsong@sohu.com