转子-轴承系统局部边界参数识别方法*
谭 祯, 李朝峰 , 太兴宇, 闻邦椿
(1.沈阳广播电视大学理工学院 沈阳,110003) (2.东北大学机械工程及自动化学院 沈阳,110819)
转子-轴承系统局部边界参数识别方法*
谭 祯1,2, 李朝峰2, 太兴宇2, 闻邦椿2
(1.沈阳广播电视大学理工学院 沈阳,110003) (2.东北大学机械工程及自动化学院 沈阳,110819)
为了提高实际工程中转子系统某一局部结构的动力特性和计算效率,便于局部振动分析并简化系统建模,提出了一种局部约束参数识别方法。考虑系统各部件间的耦合效应,对转子系统的轴和盘片结构进行分解,建立子系统与主系统。通过动力学方程推导,获得局部求解,识别子系统与主系统的边界单元约束刚度与阻尼。通过识别的约束刚度阻尼建立子系统,计算其各个节点的响应,并将其与整体模型的对应节点响应结果进行对比验证,证明了该方法的可行性。该方法为旋转构件局部结构的建模与振动分析提供了便利。
转子系统; 参数识别; 动力学模型; 刚度; 阻尼
引言
旋转机械中的转子结构中通常由多个转子和多个零部件配合组成,系统较为复杂且各个部件之间有强烈的耦合效应。为设计和研制机械结构,了解其工作状况下的特性,不仅要对盘片建模,还需要建立整机有限元模型,分析其振动效应和动力特性[1-5]。对整机及组件的建模,零件和零件之间的联接是通过限制边界条件来实现。将整个结构建立模型进行分析计算,会给建模带来很大困难,也会使整机有限元模型的自由度过于庞大,耗费较多时间和资源,造成研制费昂贵、设计周期长等问题。文献[6]研究了支承及非支承机匣系统中空心幅板类零部件、孔类零部件和附件等典型结构在整机建模中结构简化的处理方法。毛文哲等[7]通过有限元方法建立连接刚度的体单元、加厚板单元和多点约束单元等有限元分析模型,对比了不同建模方式对结构动力学特性的影响。曾嫣等[8]对转子系统的轴系关键部件进行简化,建立转子的动力学模型。以上研究均是对不同结构建模方式进行简化,以达到简化整体模型的目的,忽略了动态连接刚度的影响。笔者通过识别局部位置参数来建立子系统,简化整体模型,考虑了在不同转速、不同位置下连接刚度的变化。左曙光等[9]为研究橡胶衬套轴向静、动态特性,提出一种模型,并通过试验结果识别动刚度和阻尼系数。文献[10]对有限元模型的支承位置进行刚度识别,为本研究的参数识别提供了依据。
笔者提出了一种局部约束参数识别的方法,将转子系统的轴和盘片结构分解成多个子系统,并考虑其各个子系统之间的耦合效应。在子系统中将一组单元用矩阵凝聚为一个单元,对约束部分的局部单元参数进行识别,识别后的参数可对子系统单独建模分析。同时可将多个子系统建立连接,简化整个系统的建模过程,减少计算分析时间。
1 转子系统的有限元模型
笔者以一典型转子结构模型来实现和验证局部边界参数识别方法对简化系统建模的可行性。转子系统的相关参数为:转子轴半径r=10 mm,长度l=330 mm,转盘外径R=50 mm,转盘厚度H=20 mm。图1为经过离散后的有限元模型图,根据结构特征将其分为12个单元、13个节点。支承分别在第2和第12节点处,转盘质心位于第7节点处。图中圆点表示节点,每一小段表示一个单元。转子系统的运动方程可以表示为

(1)
其中:M为整体系统的质量矩阵;C为阻尼矩阵;K为刚度矩阵;Q为位移响应;F为不平衡力。
系统中的材料阻尼以Rayleigh阻尼形式定义为
D=αM+βK
(2)

简支系统固有频率(圆频率)第1阶为807 rad/s,第2阶为5 312 rad/s,阻尼系数ζ1为0.05,ζ2为0.08。

图1 柔性转子系统有限元模型Fig.1 Finite element model of flexibility rotor system
2 转子模型边界参数识别的推导
为简化系统结构并考虑各个系统之间的耦合关系,将系统的动力学方程根据其边界单元的位置将式(1)分解,建立子系统,获得局部求解,再组集到整个求解中。分解时将系统的节点位移分成两组:第1组是同子系统或单元共用,具有位移协调关系,属于边界节点位移,用下标1表示;第2组是与子系统或单元没有位移协调关系,用下标2表示,边界单元包含子系统单元的结构力和边界的约束力。将第1组节点刚度阻尼分解出边界约束刚度项和阻尼项,分别为Kq,Cq,式(1)可分解为
(3)
设式(1)的稳态响应为Q=qcosωt+psinωt,F=Acosωt+Bsinωt。其中:ω表示旋转角频率。代入式(3)得
(4)
其中:
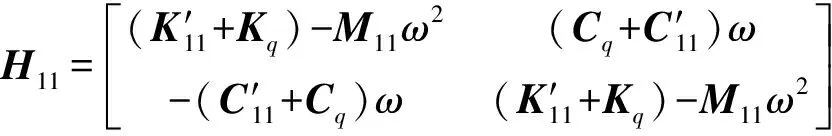
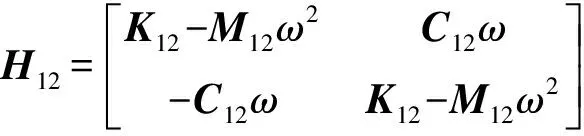

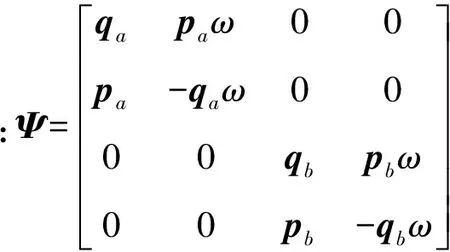

(5)
求解参数为Kq,Cq,A2,B2,式(5)中4个方程求解8个未知数,采用最小二乘法求解不同转速建立的方程。将识别得到的约束刚度和阻尼与结构刚度和材料阻尼进行组集,得到子系统的整体刚度阻尼矩阵。
如需要分析子系统的振动工作特性,可通过该方法识别的整体刚度阻尼矩阵建立子系统有限元模型,简化建模的复杂程度。
将式(4)进一步演化,得
(6)

HBXqp=XAB
(7)
将上述等式反复赋给不同的子系统,则整个系统的刚度阻尼矩阵为
(8)
一旦计算出边界节点或子系统节点位移,则所有子系统的位移和应力便可求出。由于边界刚度阻尼矩阵HB的阶数远小于子系统刚度阻尼矩阵的阶数,使得最后组集各个子系统所得到的结构刚度阻尼矩阵的阶数大大降低,故该方法可应用于大型转子结构的振动问题分析。
3 局部模型参数识别
3.1 模型的建立
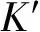

图2 子系统模型示意图Fig.2 Schematic diagram of subsystem model
设圆盘的初始不平衡量为5×10-4g·m,偏心初始相位φ1=φ2=0,相位差为Δφ=0,施加不平衡载荷,设置不同转速,计算得到各节点在不同转速下的位移响应,为参数的识别提供条件。
3.2 基于模型振动响应的局部位置参数识别
为获得算例中边界节点的约束刚度和阻尼数值,实现局部位置参数的识别,完成系统建模,笔者按照介绍的动力学方程的推导过程,分别建立子系统有限元模型和整体有限元模型,子系统在阻尼计算中采用默认值设置边界条件,计算子系统1和子系统2的临界转速。子系统1的1阶临界转速为2 325 rad/s,2阶临界转速为10 696 rad/s,子系统2的1阶临界转速为1 258 rad/s,2阶临界转速为7 358 rad/s。为了考虑高阶临界转速对识别参数的影响,设定该转子系统的转速从100 rad/s~12 000 rad/s变化。通过动力响应计算,得到转子系统边界节点的位移响应,识别出位移响应系数。将谐响应计算的结果导入识别计算程序中,求得Xqp。使用最小二乘法,通过式(5)求得边界单元的约束刚度和阻尼。将边界单元的结构刚度和材料阻尼与识别所得的约束刚度和阻尼进行组集,得到子系统的整体刚度阻尼矩阵,建立子系统模型。通过式(8)组集整体转子系统模型。
由于篇幅所限,列出部分关键转速下的识别参数,如表1所示。绘制曲线如图3所示。对结果进行分析发现,识别的参数与子系统的临界转速有一定关系,与整体模型的临界转速关系不大。图3中,A点转速为1 200 rad/s,B点为1 400 rad/s,C点为2 200 rad/s,D点为2 500 rad/s,E点为1 300 rad/s,F点为2 300 rad/s,与子系统的简支模型的临界转速数据对照,突变位置均在子系统的一阶临界转速附近。这是由于在一阶临界转速下,弯曲方向上位移响应突然增大。由于笔者采用的模型为对称模型,二阶振型变化不明显,所以在二阶临界转速附近,识别参数没有明显变化。
不同子系统变化趋势基本相同。对于不同的子系统模型,子系统截取的轴段长度增加,其二阶临界转速降低,刚度阻尼值产生突变时对应的转速也随之降低。从图3可以看出:由于圆盘位于轴的中点,所以左右边界节点识别刚度阻尼基本相同; 在远离一阶临界转速下,不同子系统的识别参数数值接近,说明一阶临界转速对识别参数的结果影响较大。
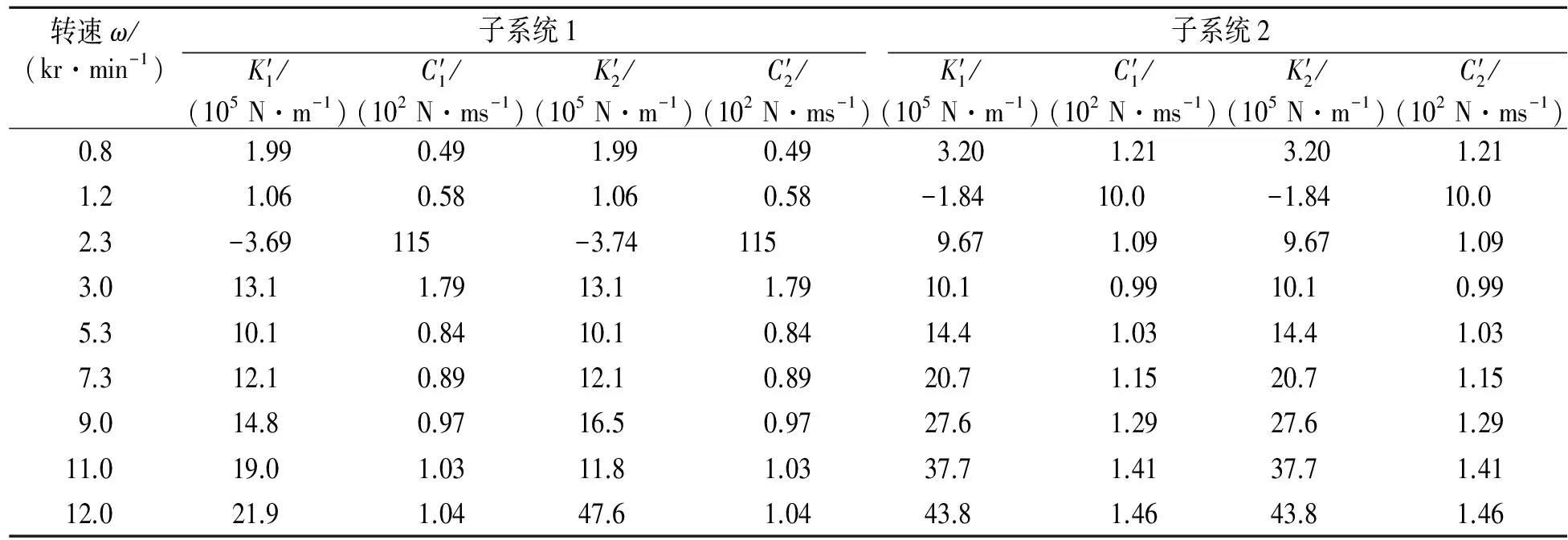
表1 部分识别的刚度和阻尼

图3 随转速变化识别参数曲线Fig.3 The change curves of identified parameters with rotate speeds
4 结果验证

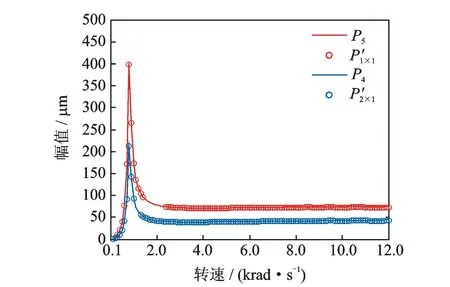
图4 测量点的随转速变化的位移幅值曲线Fig.4 The amplitudes curves of measured displacement with rotating speeds
为了比较子系统和整体系统的时域特性,并由于篇幅所限,笔者选择了一组特殊转速绘制子系统模型与整体系统模型对应边界节点的位移响应时域图,如图5所示。图例与图4中的图例符号含义相同。当转速为800 rad/s时,与整体系统的一阶临界转速806 rad/s接近,其振动幅值较大。随着转速的增大,响应曲线的密度增大,振动的频率增大,该变化趋势与实际情况相符。在转速为2 000 rad/s时,在子系统1的一阶临界转速附近所识别的刚度产生突变,从而位移响应与整体模型对应不上,8 000 rad/s和11 000 rad/s分别与子系统1、子系统2的二阶临界转速接近。从曲线的吻合程度可以看出,由识别参数建立的局部分析模型所得的位移响应与整体模型位移响应的相位与幅值等基本重合,吻合得非常理想,在其他转速下结果均理想。
通过计算分析对比可以看出,在不同子系统中,不同转速下识别刚度和阻尼数值变化趋势基本一致,其数值与子系统的一阶临界转速关系密切。在一阶临界转速下,识别的参数会有明显变动。在其他转速下,经计算其响应计算对比,所建立的整体模型与子系统模型结果基本一致,说明识别得到的刚度和阻尼基本可靠,同时也说明通过识别的约束参数建立的子系统能包含整体系统的耦合效应,可单独作为分析对象,实现对结构的简化。
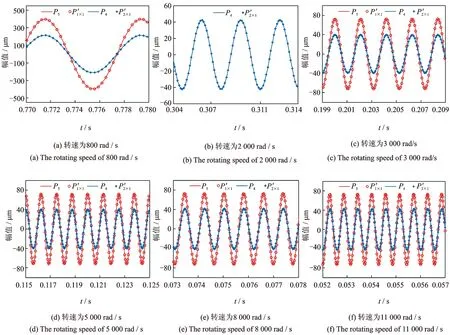
图5 测量点在不同转速下的x方向位移响应曲线Fig.5 The response curves of measured displacement in x with different rotating speeds
5 结 论
1) 识别的约束参数在子系统弹支模型的一阶临界转速时出现波动,在其他转速下变化趋势基本一致。验证结果表明,所识别参数可以保证子系统的动力响应与原系统一致。
2) 由于所分析的转子系统为一对称结构,因此参数识别结果在二阶临界转速附近并没有较大的波动,而在实际工程应用中这种现象可以得到避免。
3) 该方法可以对复杂转子系统进行局部动力学参数识别,可为旋转构件局部结构的建模与振动分析提供便利,达到节约计算资源的目的。
[1] Ou Yuanxia, Li Ping. Mode synthesis analysis of vibration of entire engine[J]. Journal of Aerospace Power, 2007,2(3):209-214.
[2] 陈果.双转子航空发动机整机振动建模与分析[J].振动工程学报,2011,24(6):619-632.
Chen Guo. Vibration modeling and analysis for dual-rotor aero-engine[J]. Journal of Vibration Engineering, 2011,24(6):619-632. (in Chinese)
[3] Chen Guo. A new rotor-ball bearing-stator coupling dynamic model for whole aero-engine vibration[J]. Journal of Vibration and Acoustics, 2009,131(6):610091-610099.
[4] 史峰,杜建标,程礼.双转子动力学研究[J].机械与电子,2008(10):56-58.
Shi feng, Du Jianbiao, Cheng li. The studies on the dynamics of the double-rotors system[J]. Machinery and Electrnics, 2008(10):56-58. (in Chinese)
[5] 马辉,王奇斌,黄婧,等.不同自由度耦合斜齿轮转子系统的振动特性[J].振动、测试与诊断,2014,34(4):650-657.
Ma Hui, Wang Qibin, Huang Jing, et al. Vibration characteristics analysis of a helical gear rotor system considering different degrees of freedom coupling[J]. Journal of Vibration, Measurement and Diagnosis, 2014,34(4):650-657. (in Chinese)
[6] 高金海,洪杰.航空发动机整机动力特性建模技术研究[J].战术导弹技术,2006(3):29-35.
Gao Jinhai, Hong Jie. Study of modeling technique for dynamic characteristics of engine casing[J]. Tactical Missile Technology, 2006(3):29-35. (in Chinese)
[7] 毛文哲,雷勇军.结构动力学特性分析中连接刚度的有限元建模对比研究[J]. 试验技术与试验机,2007(2):4-7.
Mao Wenzhe, Lei Yongjun. Comparison analysis of FEM modeling of connected stiffness for structural dynamics[J]. Test Technology and Testing Machine, 2007(2):4-7. (in Chinese)
[8] 曾嫣,樊久铭,姚大坤.汽轮机转子动力学建模[J].电站系统工程,2007,23(4):27-28.
Zeng Yan, Fan Jiuming, Yao Dakun. Modeling on dynamics of trubine rotor[J]. Power System Engineering, 2007,23(4):27-28. (in Chinese)
[9] 左曙光,李凯,吴旭东.一种新型橡胶衬套理论模型及其参数识别[J].振动、测试与诊断,2014,34(3):433-438.
Zuo Shuguang, Li Kai, Wu Xudong. A novel theoretical model of rubber bushing and parameter identification[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(3):433-438. (in Chinese)
[10]Han Qinkai, Yao Hongliang, Wen Bangchun. Parameter identifications for a rotor system based on its finite element model and with varying speeds[J]. Advances in Vibration Engineering, 2008,7:365-376.
*国家科技支撑计划资助项目(2009BAG12A01-F01-3);国家自然科学基金青年基金资助项目(51105063)
2013-02-01;
2013-06-26
10.16450/j.cnki.issn.1004-6801.2015.01.012
TH113
谭祯,女,1981年6月生,博士、副教授。主要研究方向为振动分析与应用、多场耦合分析等。曾发表《不同湍流模型旋转叶片气固耦合动力学特性研究》(《振动与冲击》2013年第32卷第11期)等论文。 E-mail:tanz-hen@126.com

