一方不能独立生存的离散偏利合作模型研究

陈凤德,林椿涛,杨丽娅

(福州大学 数学与计算机科学学院,福建 福州 350116)

一方不能独立生存的离散偏利合作模型研究

陈凤德,林椿涛,杨丽娅

(福州大学 数学与计算机科学学院,福建 福州 350116)

首次提出了一类一方不能独立生存的离散偏利合作模型,探讨了系统的持久性、绝灭性和稳定性等.研究表明,在合作效益较小时,某一种群将绝灭,而在合作效益足够大后,两个种群都能持久生存.

偏利合作系统; 绝灭性; 持久性; 全局吸引性

本文采用如下记号:

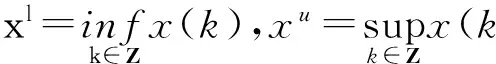
已经有很多学者对合作种群模型的动力学行为展开了研究[1-5],然而,至今为止,有关偏利合作种群模型的研究工作还很少.祝占法等提出了如下一方不能独立生存的两种群偏利合作模型[5]:

(1)

借助向量场分析的方法研究了系统(1) 的各个平衡点的稳定性和系统的轨线走向问题,随后进一步考虑了环境毒素对种群的影响,得到了所研究模型种群弱平均持续生存和绝灭的充分性条件.式中,x≥0,y≥0,a1<0,a2>0,b1<0,c2<0,c1>0均为常数.最近,杨丽娅等[6]认为实际的生态环境都是随着时间的变化而变化的,因此,考虑非自治的一方不能独立生存的偏利合作系统更为符合实际,他们提出了如下模型:

(2)

研究表明,在合作效益较小时,种群将仍然绝灭,而在合作效益足够大后,两个种群都能持久生存,随后进一步探讨了系统的稳定性问题.式中,ai(t),bi(t)(i=1,2),c1(t)均为正的有上下界的连续函数;x1(t)是第一个种群在t时刻的生长密度,x2(t)是第二个种群在t时刻的生长密度.

近年来,学者们已经认识到,对生命短、世代不重叠的种群,或者虽然是生命长、世代重叠的种群,但在其数量比较少时,用差分方程(或者说离散动力模型)来表示更为合理.

本文研究如下与系统(2)相对应的离散偏利合作模型:

(3)

式中,ai(k),bi(k),c1(k)均为正的有上下界的序列;x1(k)是第一个种群第k代的种群密度,x2(k)是第二个种群第k代的种群密度.显然,在没有第二个种群的帮助下,第一个种群满足方程x1(k+1)=x1(k)exp{-a1(k)-b1(k)x1(k)},由此容易看出其最终走向绝灭.本文的目的旨在探讨第二个种群如何影响第一个种群的动力学行为,探讨系统的持久性、绝灭性和全局吸引性.主要结果如下.

引理1[7]假设{x(k)}>0,a(k),b(k)是有正的上下界的非负序列,对k∈N,有

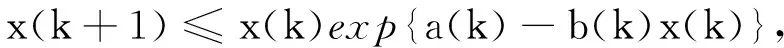
则

引理2[7]假设x(N0)>0,a(k),b(k)是有正的上下界的非负序列,{x(k)}满足

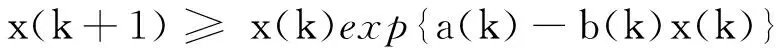
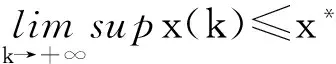
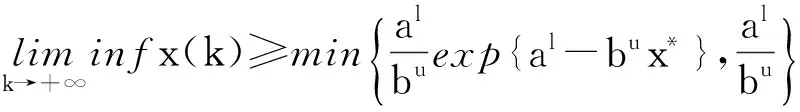
引理3[8]假设{x(k)}>0,a(k),b(k)是有正的上下界的非负序列,对k∈N,有

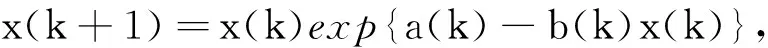
则

其中

引理4系统(3)的第二个种群恒为持久的.

证明 由系统(3)的第二个方程x2(k+1)=x2(k)exp{a2(k)-b2(k)x2(k)}和引理3有

(4)

式中,

(5)

证明 第二个种群的持久性已经由引理4证得,下面探讨第一个种群的绝灭性.

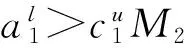
(6)

由系统(3)的第一个方程以及式(4)和式(5)可知,当k>K1时,有

(7)

也就是有

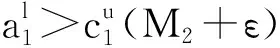
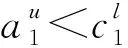
(8)

由式(4) 知,对上述ε>0,存在K2,当k>K2时,有

(9)

由式(9)并结合系统(3) 的第一个方程可知,当k>K2时,有

由引理1有

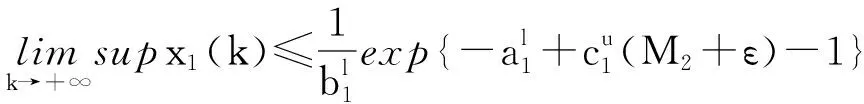
令ε→0,有

(10)

此外,由式(9)并结合系统(3) 的第一个方程可知,当k>K2时,有

由引理2有

令ε→0,有

(11)

下面探讨系统(3)的稳定性.

定理3假设定理2的条件成立,此外,进一步假设

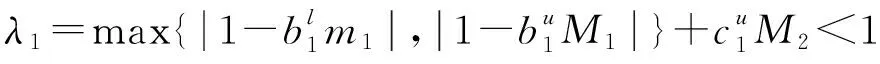
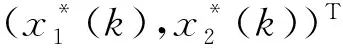
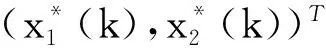
(12)

则有

(13)

另一方面,直接由x1(k)满足系统(3)的第一个方程也可得到

其中

整理可得

(14)

类似于上述整理,由系统(3)的第二个方程也可得到

(15)

借助于中值定理,由式(14)和式(15)有

(16)

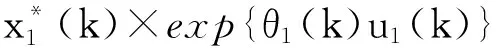
(17)

由定理2知,对上述ε>0,存在K3,当k>K3时,有

从而由式(16)易得

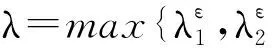
注意到λ<1,可得

由式(12)易得

注:本文提出并研究了一类离散的一方不能独立生存的偏利合作系统.由定理1可知,种间合作效益比较小、第一个种群的死亡率比较大时,原来不能独立生存的一方仍然最终绝灭,而另外一个种群是恒持久的;种间合作效益比较大、第一个种群的死亡率比较小时,由定理2知两个种群可以长久共存,这说明两种群间的合作强度直接决定第一个种群的持久生存或者绝灭.

[1]ChenFD.PermanenceofaDiscreteN-speciesCooperationSystemwithTimeDelaysandFeedbackControls[J].AppliedMathematicsandComputation,2007,186(1):23-29.

[2] Chen L J,Xie X D.Permanence of an-species Cooperation System with Continuous Time Delays and Feedback Controls[J].Nonlinear Analysis: Real World Applications,2011,12(1):34-38.

[3] Yang W S,Li X P.Permanence of a Discrete NonlinearN-species Cooperation System with Time Delays and Feedback Controls[J].Applied Mathematics and Computation,2011,218(7):3581-3586.

[4] 陈凤德,谢向东.合作种群模型动力学研究[M].北京: 科学出版社,2014.

(Chen Fengde,Xie Xiangdong.Study on the Dynamic Behaviors of Cooperative Population[M].Beijing: Science Press,2014.)

[5] 祝占法,栗永安,徐芳.具有偏利关系的Lotka-Volterra模型[J].重庆工学院学报:自然科学版,2007,21(10):59-62.

(Zhu Zhanfa,Li Yongan,Xu Fang.Mathematical Analysis on Commensalism Lotka-Volterra Model of Populations[J].Journal of Congqing Institute of Technology: Natural Science Edition,2007,21(10):59-62.)

[6] 杨丽娅,韩荣玉,薛亚龙,等.一方不能独立生存的非自治偏利合作模型研究[J].三明学院学报,2014,31(6):15-18.

(Yang Liya,Han Rongyu,Xue Yalong,et al.On a Nonautonomous Obligate Lotka-Volterra Model[J].Journal of Sanming University,2014,31(6):15-18.)

[7] Chen F D.Permanence for the Discrete Mutualism Model with Time Delays[J].Mathematical and Computer Modelling,2008,47(3):431-435.

[8] 吴玉敏.四类具有避难所的非自治捕食-食饵种群的动力学行为研究[D].福州:福州大学,2012.

(Wu Yumin.Dynamic Behaviors of Four Kinds of Non-Autonomous Predator Prey Models Incorporating a Prey Refuge[D].Fuzhou: Fuzhou University,2012.)

【责任编辑: 李 艳】

On a Discrete Obligate Lotka-Volterra Model with One Party can not Survive Independently

ChenFengde,LinChuntao,YangLiya

(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China)

A discrete obligate Lotka-Volterra model was proposed,the permanence,extinction and global attractivity of the system are investigated.The study shows that,when cooperation benefits are small,one population maybe driven to extinct; while if the cooperation benefits are large enough,the two populations can persistence.

obligate Lotka-Volterra model; extinction; permanence; global attractivity

2015-01-14

国家自然科学基金资助项目(11201075,11361068); 福建省自然科学基金资助项目(2013J01010).

陈凤德(1974-),男,福建屏南人,福州大学教授.

2095-5456(2015)04-0336-04

O 175.14

A