四维不定空间中的一类曲面

关红钧,聂 颖

(沈阳大学 师范学院,辽宁 沈阳 110044)

四维不定空间中的一类曲面

关红钧,聂 颖

(沈阳大学 师范学院,辽宁 沈阳 110044)

研究了四维伪双曲空间中的一类Marginally Trapped洛伦兹曲面,对具有平行平均曲率向量的这类曲面进行了分类,一共得到了6类曲面,为黑洞理论的研究提供了一定的理论支持.

洛伦兹曲面; Marginally Trapped 曲面; 平均曲率

具有平行平均曲率向量的子流形在微分几何、调和映射以及物理学中具有重要的作用.早在20世纪70年代,Chen分类了欧氏空间中具有平行平均曲率向量的曲面[1].在文献[2-3]中,伪欧氏空间中具有平行平均曲率向量的类空曲面被完全分类.由于洛伦兹曲面的度量是不定的,对其进行研究更复杂一些.伪欧氏空间中具有平行平均曲率向量的洛伦兹曲面已经被完全分类了,见文献[4-5].

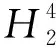
1 预备知识

1.1 基本公式

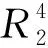
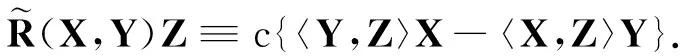
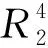
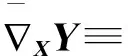
(1)

(2)

式中,h,A和D分别为第二基本形式、形状算子以及法联络.第二基本形式h和形状算子A具有如下关系:

(3)

平均曲率为

Gauss方程和Codazzi方程分别为

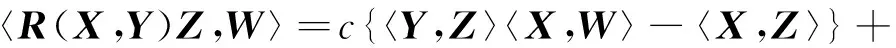
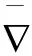
(4)

记RD为法曲率张量:

则Ricci方程为

1.2 光 锥

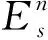
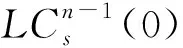
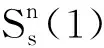
1.3 活动标架

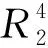
(5)

(6)

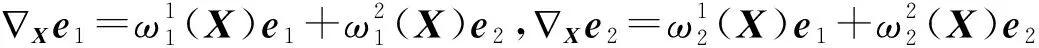
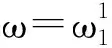
(7)

令ω(e1)=ω1,ω(e2)=ω2.类似地,存在一形式φ,使得:

(8)

1.4 引 理

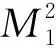
g=-m2(x,y)(dx⊗dy+dy⊗dx).

其中,m(x,y)为正函数,且曲面的Levi-Civita联络为:

(9)

曲面的高斯曲率为

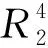
(1) φ=0,这意味着RD=0;

(2) 〈H,H〉是常数.

2 主要定理及其证明

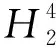
(2) 曲率为-1的洛伦兹曲面,定义为

其中,p(y)是位于光锥LC中的曲线,q(y)是满足

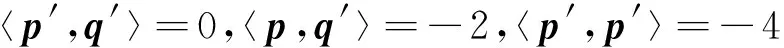
的零曲线.

(3) 曲率为-1的洛伦兹曲面且位于

中,定义为

其中:

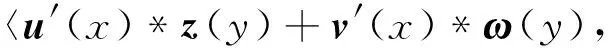
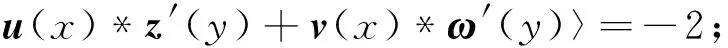
(6) 平坦的洛伦兹曲面,定义为

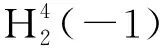
由于M具有平行平均曲率向量H,由引理2知

(10)

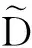
(11)

其中,α,β,γ,δ是实值函数,则:

(12)

由方程(11)和方程(12) ,得到

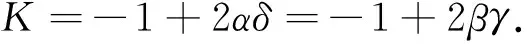
(13)

情况Ⅰ:K≠-1.

此时,α,β,δ,γ≠0.由式(7)和式(11)知Codazzi方程退化为

(14)

由式(14) 和αδ=βγ知

则存在一个非零实数c,满足:

(15)

由式(7)和式(14)知

则存在一个坐标系{x,y},使得

且

(16)

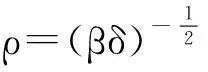
(17)

此外,由式(11)、式(12)、式(15)和式(16),得:

(18)

(19)

(20)

此方程组的可积性条件满足Poisson方程:

(21)

另外,若令

则:

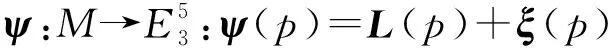
且

(22)

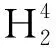
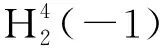
所以

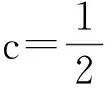
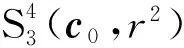
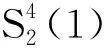
从而

如果M是非平坦的,那么可以得到定理中的(5).

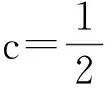
(23)

(24)

解微分方程(24)得

L=c1sin(2u)+c2cos(2u)+c3υ+c4υ2+c5,

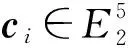
情况Ⅱ:K=-1.

由式(13)知αδ=βγ=0,且M是曲率为-1的洛伦兹曲面.由引理1,在曲面M上选取坐标系{x,y},则M的度量张量为

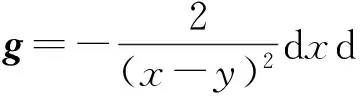
(25)

曲面M的Levi-Civita联络为

(26)

且式(18)为

(27)

由式(26)和式(27)知

且满足:

(28)

(29)

(30)

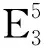
因此,存在函数p(x)和q(y),使得α=p(x)×(x-y)2,γ=q(y)(x-y)2,则式(28)和式(30)为

(31)

解方程组(31)得

其中

由式(29)知c2-c3-2e3=0.重新选择适当的初始条件,可以得到定理中的(1).

2)δ=γ=0.在这种情况下,式(30) 成为

解方程,得到

(32)

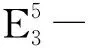
知:

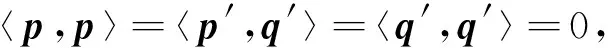
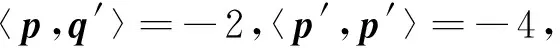
即得到定理中的(2).

3)α=β=0.交换x和y,也能得到定理中的(2).

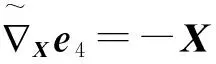
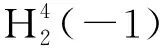
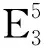
另外,式(28)～式(30) 的可积性条件为:

(33)

所以,存在函数c1(x)和c2(y),使得

(34)

则式(28)和式(30)变成

(35)

解方程组(35)得

(36)

式中,f(x,y)是位于光锥LC(c0)中的函数,且满足

(37)

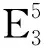
则式(37)表明

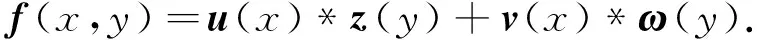
(38)

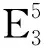
因此,式(36)和式(38)表明

(39)

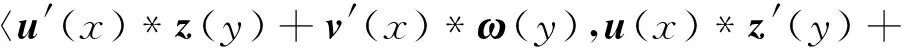
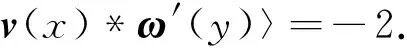
这就是定理中的(3).

3 结 语

[1] Chen B Y.Surfaces with Parallel Mean Curvature Vector[J].Bulletin of the American Mathematical Society,1972,78(5):709-710.

[2]ChenBY.ClassificationofSpatialSurfaceswithParallelMeanCurvatureVectorinPseudo-EuclideanSpacesofArbitraryDimension[J].JournalofMathematicalPhysics,2009,50(4):1-14.

[3]ChenBY.CompleteClassificationofSpatialSurfaceswithParallelMeanCurvatureVectorinArbitraryNon-flatPseudo-RiemannianSpaceForms[J].CentralEuropeanJournalofChemistry,2009,7(3):400-428.

[4]ChenBY.CompleteClassificationofLorentzSurfaceswithParallelMeanCurvatureVectorinArbitraryPseudo-EuclideanSpace[J].KyushuJournalofMathematics,2010,64(2):261-279.

[5]FuY,HouZH.ClassificationofLorentzianSurfaceswithParallelMeanCurvatureVectorinPseudo-EuclideanSpaces[J].JournalofMathematicalAnalysisandApplications,2010,371(1):25-40.

[6] 张秀玲,臧佳音,樊红敏,等.改进的万有引力搜索算法[J].沈阳大学学报:自然科学版,2014,26(6):468-472.

(ZhangXiuling,ZangJiayin,FanHongmin,etal.ImprovedGravitationalSearchAlgorithm[J].JournalofShenyangUniversity:NaturalScience,2014,26(6):468-472.)

[7]ChenBY.DependenceoftheGauss-CodazziEquationsandtheRicciEquationofLorentzSurface[J].PublicationesMathematicaeDebrecen,2009,74(3/4):341-349.

【责任编辑: 李 艳】

A Kind of Surface in 4-Dimensional Indefinite Space Form

GuanHongjun,NieYing

(Normal School,Shenyang University,Shenyang 110044,China)

A kind of Marginally Trapped Lorentz surfaces in 4-dimensional pse-hyperbolic space is studied.The surface with parallel mean curvature vector is classified,six kinds of surfaces are got,which could provide a theoretical support for the study of black hole theory.

Lorentz surface; Marginally Trapped surface; mean curvature

2015-01-28

辽宁省教育厅一般项目(L201482).

关红钧(1968-),女,辽宁沈阳人,沈阳大学副教授.

2095-5456(2015)04-0340-05

O 186

A