状态依赖下不确定切换线性系统有限时间有界性分析

王跃华,孙晓靓

(1.沈阳大学 师范学院,辽宁 沈阳 110041; 2.辽宁水利职业学院,辽宁 沈阳 110122)

状态依赖下不确定切换线性系统有限时间有界性分析

王跃华1,孙晓靓2

(1.沈阳大学 师范学院,辽宁 沈阳 110041; 2.辽宁水利职业学院,辽宁 沈阳 110122)

根据凸组合方法,依据状态依赖切换策略设计切换信号和Lyapunov类函数的方法,解决了一类带有不确定项的切换线性系统在外部干扰存在前提下的有限时间有界性问题,并且分析了滑膜现象产生的情况.

存在干扰; 不确定项; 状态依赖切换策略; 有限时间有界

有限时间稳定研究的是在没有外部干扰的情况下系统在较短的时间间隔里的具体行为表现,而当外部干扰存在时就变成了有限时间有界的问题.近年来,关于有限时间稳定问题的结果有很多.文献[1]研究的是带有不定项以及干扰的线性系统的有限时间稳定性和有限时间有界性问题.文献[2]考虑的是脉冲动力系统的有限时间稳定问题,文献[3]给出了设计一个动力反馈输出控制器的过程.文献[4]研究了关于带有时变时滞的切换系统基于H∞有限时间控制的观测器的问题.文献[5]中研究了一系列具有外部干扰的时变切换线性系统的有限时间稳定以及有界问题,给出了当切换系统是有限时间稳定的前提时的一组状态依赖切换信号,并且这里的状态依赖切换信号是根据单Lyapunov类函数设计的.

对于有限时间稳定以及有界问题的解决方法,目前大多数依据的是时间依赖切换策略.但有时当切换间隔没有事先给出时,就需要给出基于当前系统状态的切换策略.文献[6]研究了基于状态切换策略下的切换线性系统的有限时间稳定、有限时间有界问题,而文献[7]同样在状态切换策略下研究了切换线性系统的有限时间稳定、有限时间有界问题,并给出了带有滑膜情况的结论.本文在文献[6-7]的基础上,同样在解决带有不确定项的切换线性系统的有限时间的有界问题上,得到了可以依据状态依赖切换策略(滑膜情况考虑在内)的结论.

1 系统描述与相应问题的说明

对于一组如下形式的切换线性控制系统

(1)

(2)

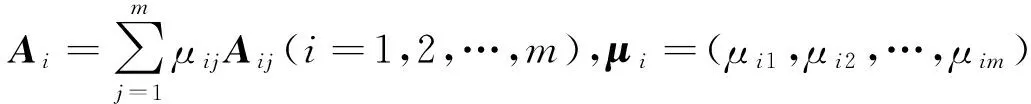
对于系统(1),选择状态反馈控制器

(3)

将式(3)代入切换线性系统(1),则可以得到如下闭环系统

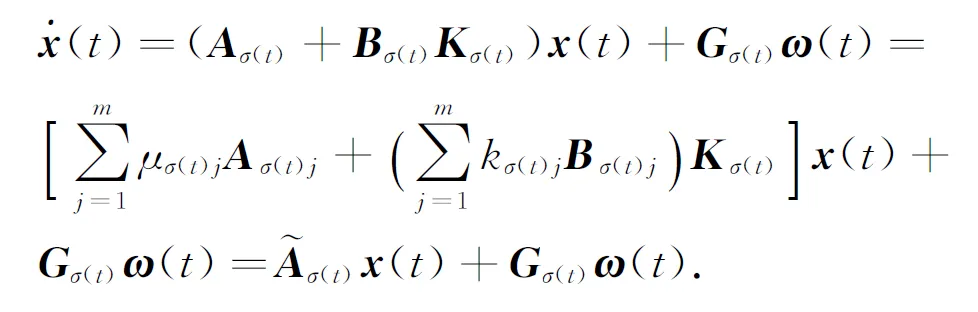
2 系统假设与相关引理

假设1x(t)的曲线是处处连续的,也就是在切换的瞬间切换线性系统的状态x(t)是不会发生跳跃的.

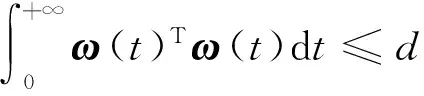
为了找到切换线性系统的每一个子系统的李雅普诺夫类函数,分割整个状态空间Rn成若干个子空间,记作Ωi.为了达到这个目的,需将整个状态空间被这些Ωi区间覆盖,即满足如下的覆盖条件即可

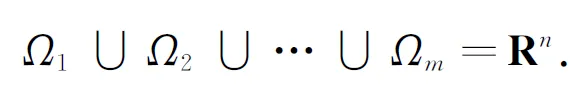
(4)

要实现将问题简化的目的,假设每个子空间Ωi都可以表示成以下二次形式

(5)

式中,Qi∈Rn×n为对称矩阵.

如下引理即可帮助实现覆盖条件.

引理1[8](覆盖条件) 如果对于每一个状态x∈Rn,都有

(6)

成立,那么Ω1∪Ω2∪…∪Ωm=Rn.其中,θi≥0,i=1,2,…,m.

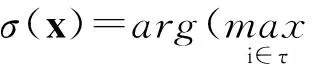
3 有限时间有界的定义

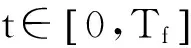
4 有限时间有界的充分条件及证明

将系统(1)选择切换状态反馈控制器u(t)=Kσ(t)x(t),将它代入切换线性系统(1),即可得到如下形式的闭环系统

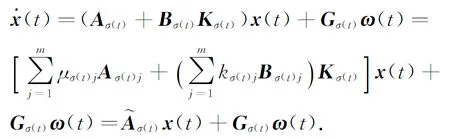
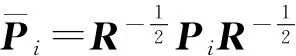
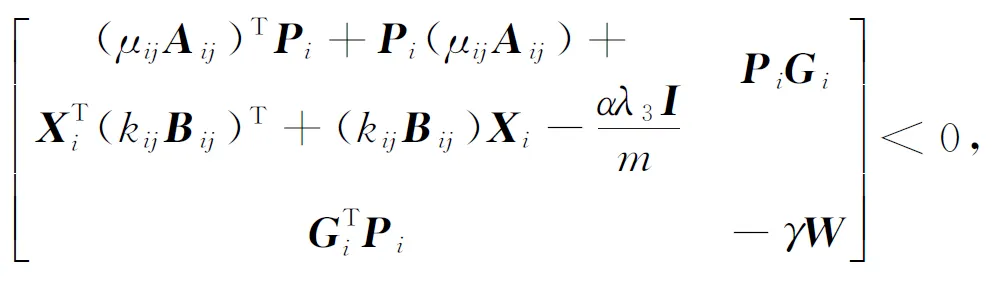
(7)

(8)

(9)

(10)

(11)

切换策略为

(12)

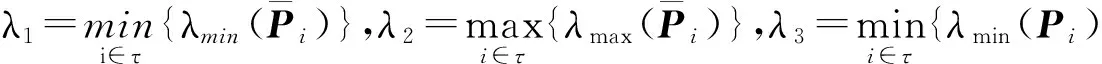
证明 令V(x)=Vi(x)=xTPix,对每一个子系统的能量测量,选用李雅普诺夫备选函数.不妨设i=1,2,j=1,2.对于i,j为其他值的一般情况也是明显的.

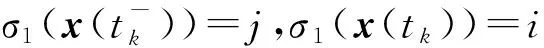
(13)

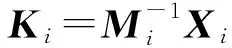
即:

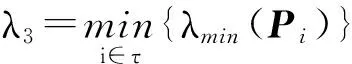
(14)

对式(14)由tk到t积分可得

(15)

(16)

由式(15)和式(16),可得

(17)

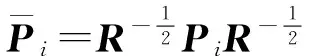
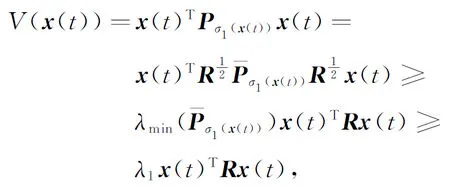
(18)

(19)

由定义以及式(17)～式(19),可以得到

(20)

根据定义可知,连续时间切换线性系统(1)是有限时间有界的.

第二种情况:当产生滑膜现象时.此时,状态满足

即滑膜现象产生于子系统间发生转换之时.滑膜现象可能出现的区域为Ωi,j处,此时满足如下关系式:xTQix=xTQjx≥0.滑膜现象会导致切换表面稳定或不稳定的情况发生,因此,需要研究的是在滑膜现象发生时定理中给定的条件能否保证系统仍然是有限时间有界的.当滑膜现象在Ωi,j处发生时,即意味着如下关系式成立

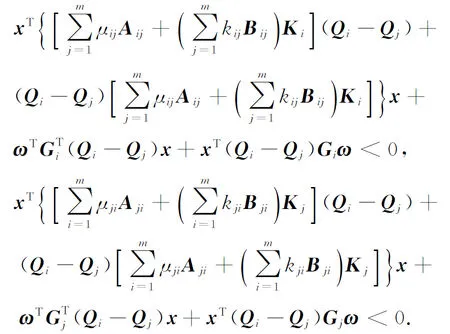
其中,i=1,2,…,m,j=1,2,…,m.即

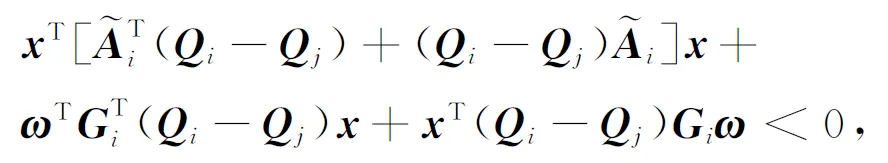
(21)

(22)

在滑膜表面的系统可以表示成

(23)

式中,ρ∈[0,1].由式(8)以及前面的条件可得:

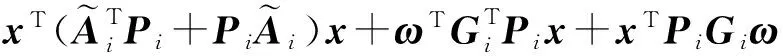
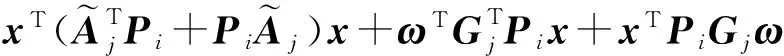
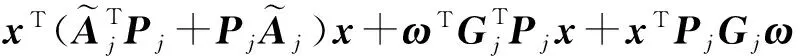
由此可得:

(24)

(25)

式(24)和式(25)相加可得

(26)

同时可得到:

(27)

(28)

式(27)和式(28)相加可以得到

(29)

由此可得:

(30)

(31)

因此,在滑膜表面的系统中,上述条件同样适用.证明过程的其他部分和第一种情况是相同的.

5 结 语

依据状态依赖切换策略,在外部干扰存在的前提下,主要研究了带有不确定项的切换系统的有限时间有界性问题.相对于运用时间依赖切换策略来说,状态依赖切换策略更显复杂,鉴于切换常数一般不会事先给出,状态依赖切换策略就更具实用性.

[1] Amato F,Ariola M,Dorato P.Finite-Time Control of Linear Systems Subject to Parametric Uncertainties and Disturbances[J].Automatica,2001,37(9):1459-1463.

[2]GarciaG,TarbouriechS,BernussouJ.Finite-TimeStabilizationofLinearTime-VaryingContinuousSystems[J].IEEETransactionsonAutomaticControl,2009,54(2):364-369.

[3]AmatoF,AriolaM,CosentinoC.Finite-TimeStabilizationviaDynamicOutputFeedback[J].Automatica,2006,42(2):337-342.

[4]LiuH,ShenY,ZhaoXD.Delay-DependentObserver-BasedH1Finite-timeControlforSwitchedSystemswithTime-VaryingDelay[J].NonlinearAnalysis:HybridSystems,2012,6(3):885-898.

[5]DuHB,LinXG,LiSH.Finite-TimeBoundednessandStabilizationofSwitchedLinearSystems[J].Kybernetika,2010,46(5):870-889.

[6]ZhaoGL,WangJC.FiniteTimeStabilityandL2-GainAnalysisforSwitchedLinearSystemswithState-DependentSwitching[J].JournaloftheFranklinInstitute,2013,350(5):1075-1092.

[7]LiuH,ShenY,ZhaoXD.Finite-TimeStabilizationanBoundednessofSwitchedLinearSystemunderState-DependentSwitching[J].JournaloftheFranklinInstitute,2013,350(3):541-555.

[8]PetterssonS.SynthesisofSwitchedLinearSystems[C]∥Proceedingsofthe42ndIEEEConferenceonDecisionandControl.Maui,2003:5283-5288.

[9] 王跃华,孙晓靓.状态依赖下不确定切换线性系统有限时间稳定性分析[J].沈阳大学学报:自然科学版,2014,26(6):514-517.

(WangYuehua,SunXiaoliang.FiniteTimeStabilityofUncertainSwitchedLinearSystemsunderState-DependentSwitching[J].JournalofShenyangUniversity:NaturalScience,2014,26(6):514-517.)

【责任编辑: 李 艳】

Finite Time Boundedness of Uncertain Switched Linear Systems under State-Dependent Switching

WangYuehua1,SunXiaoliang2

(1.Normal School,Shenyang University,Shenyang 110041,China; 2.Liaoning Water Conservancy Vocational College,Shenyang 110122,China)

The problem of finite time stability of uncertain switched linear systems under state-dependent switching was studied,using the method of covex combinations and state-dependent strategy.Some sufficient conditions have been given for FTB of switched linear systems based on the method of multiple Lyapunov-like functions,and it also suits for sliding motion behaviors.

interference; uncertain item; state-dependent swithching strategy; finite time boundedness

2015-03-06

王跃华(1962-),男,天津人,沈阳大学副教授.

2095-5456(2015)04-0313-05

TP 13; TP 73

A