联合核主成分分析

王 喆,孟 芸

(华东理工大学 计算机科学与工程系,上海 200237)

联合核主成分分析

王 喆,孟 芸

(华东理工大学 计算机科学与工程系,上海 200237)

提出了KPCA的一种称为联合核主成分分析(Joint Kernel Principle Component Analysis,JKPCA)的变型,能够从输入和输出空间引出先验信息用于特征提取.首次将联合核映射应用于特征提取领域,而且在图像数据集上的实验结果表明,JKPCA是可行并有效的.

核主成分分析(KPCA); 联合核映射; 特征提取; 核方法

特征提取是模式识别中一个重要的研究方向.一个模式识别系统的成败,首先取决于所利用的特征是否较好地反映了将要研究的分类问题.对于已获得的特征,一方面,有很多与分类问题不相关,在分类器设计中会影响分类器的性能;另一方面,特征过多会带来计算量大和推广能力差等问题[1].因此,人们希望在保证分类效果的前提下使用尽可能少的特征,特征提取就是一种被广泛采用的方法.

在特征提取中,主成分分析(PCA)[2-3]是一种经典的用于从原始数据中提取紧密结构的特征提取方法.选择较少的主成分来表示数据,不但可以用作特征的降维,还可以用来消除数据中的噪声.但是主成分分析并不总是对分类有好处,如果相比于类别之间的差别来说噪声很大,那么主成分分析将找到噪声的主方向而不是人们所期望的信号的主方向[1].因此,对特征提取方法的改进是十分必要的,它直接影响到后续分类器的设计和模式识别系统的总体性能.

基于以上描述,本文首次将联合核映射(JKM)应用于特征提取领域,提出了一种新型的基于核的特征提取方法,称作联合核主成分分析(JKPCA).由于方法中采用的JKM是基于输入和输出空间的联合数据表示,JKPCA相比其他方法能够引入更多的先验信息.实验结果表明,JKPCA在由图像表示的输出数据上不仅其分类性能优于两个典型特征提取方法,即基于核的主成分分析(KPCA)和核Fisher判别分析(KFDA)[4],而且和对比算法相比,计算复杂度相当.

1 相关工作

主成分分析(PCA)投射原始数据至可以用特征值问题解决的主成分,即使用规模很小的主成分,也足够表达原始数据的主要结构.PCA是一种数学变换方法,把给定的一组相关变量通过线性变换转成另一组不相关的变量,在数学变换中保持变量的总方差不变,使具有最大方差的第一变量为第一主成分,第二变量的方差次大,并且和第一变量不相关为第二主成分,依此类推[5].因为PCA是一种线性方法,而且只能用于原始数据空间,所以Schölkopf等将PCA推广到非线性形式的核主成分分析(KPCA).实验证明,因为KPCA能够通过选择不同的核函数处理特征空间中的任意维度,它比PCA更有效且有更好的适应性[6-7].核方法之所以性能优异是因为采用了核函数,核函数即在特征空间F上的内积,它能够将原始输入空间的x∈F映射到特征空间,有Φ(x)∈F:

(1)

所以,k(xi,xj)=[φ(xi)·φ(xj)],其中,核函数k能够从原始输入空间引入先验信息.在一些文献中提到只有具有0-1损失函数形式的映射可以从输入空间为输出空间Y提供足够的信息[8-10].但同时Y可以由很多复杂的结构如图像、字符串、树或者序列等表示,只在输入空间定义核函数k会导致输出空间的信息不能得到有效利用而不能很有效地解决问题.为了能够处理以上提到的复杂输出,有些文献提出新型的核映射,称作联合核映射(JKM)[11-14].

假设输入空间中x∈F以及任意独立的输出空间y∈Y,JKM的形式如下:

(2)

式中,Ψ表示输入和输出空间中一些特征表示组合之间的映射.更进一步地,利用联合特征表示的内积,一个联合核函数可以如下定义:

(3)

JKM已经被证明能够很好地处理由多个独立变量构成的输出.

KPCA采用了式(1)中表示的常规核映射,因此,KPCA继承了式(1)中在处理复杂输出方面的缺点.为了克服这个缺点,本文将类似于式(2)中的JKM应用到KPCA,提出了基于核的特征提取方法,称作联合核主成分分析(JKPCA).

2 联合核主成分分析

2.1 特征提取

给定一组训练集(x1,y1),…,(xN,yN)∈X×Y,其中,输入空间X和输出空间Y都可以用向量、图像或者树型结构来表示.通过式(2)描述的JKM,能够映射输入和输出空间的联合表示(x,y)至φ(x,y)∈F,其中,φ(x,y)是一个向量且属于生成的联合特征空间F.因此,在联合特征空间F中,试图找到一个线性变换向量ω∈F,使得投影φ(x,y)在ω有

(4)

为了找到一个较好的转换向量ω,使投影范围r能够在ω方向上表示φ(x,y)的主要结构,本文引入投影样本的总散度来衡量ω,其准则函数是:

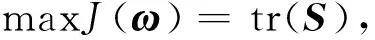
(5)

函数(5)中提到的S表示投影样本的协方差矩阵,其中,tr(S)是S的迹.准则函数(5)可以保证投影r能够保持原始样本φ(x,y)在转换向量ω方向上的主要结构.投影样本的协方差矩阵S可以由训练样本直接计算得到:

(6)

定义样本协方差矩阵C有如下式所示的形式:

(7)

把式(7)代入式(5)可以得到:

(8)

进一步地,最大化式(8)相当于解决了如下特征值问题:

(9)

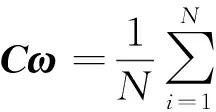
(10)

所以,针对所有的训练样本φ(xk,yk)(k=1,…,N),式(9)能够变换为

(11)

把式(7)和式(10)代入式(11)可以得到

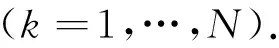
(12)

定义一个联合核矩阵K[11-12]:

(13)

则式(12)可以写成

(14)

式中,αvec是一个列向量,αvec=[α1,…,αN]T.求解式(14)又相当于求解如下特征值问题:

(15)

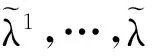
(16)

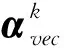
假设一组测试数据(z,y)能够映射到联合特征空间F的φ(z,y),按如下方式将φ(z,y)投影到第k个转换方向ωk:

(17)

利用W=[ω1,…,ωp],则从φ(z,y)提取的特征可以表示为

(18)

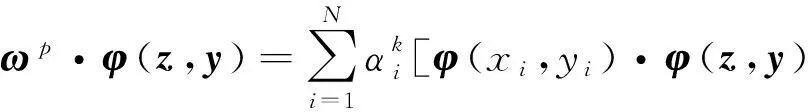
2.2 分类算法

通常情况下,测试数据(z,y)中的输出值y是未知的,但是在特征提取式(18)的过程中,对给定样本z对应的y的估计是十分必要的.本文通过如下式子得到z的输出y:

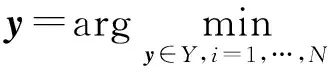
(19)

式中,Y为训练集输出(y1,…,yN)的集合.进一步地,假设对于(xi,yi)和(xj,yj),如果存在yi=yj,那么φ(xi,yi)和φ(xj,yj)投影之间的距离也是很小的;否则它们之间的距离会很大.另外要注意的是,在使用JKPCA投影的过程中,对于一个给定的测试样本,它的输出y也是可以得到的.

JKPCA的算法设计总结如下:

(1) 通过式(13)计算矩阵K;

(2) 计算式(15)的特征值;

(3) 通过式(16)正规化步骤(2)得到的特征值;

(4) 通过式(18)从测试数据(z,y)提取特征,同时,通过式(19)从z里获取输出y.

2.3 非集中型样本

上节中认为训练样本(x1,y1),…,(xN,yN)在联合特征空间F中是集中的,本节讨论一般情况即不集中的样本.假设一个训练样本集(x1,y1),…,(xN,yN)∈X×Y能够用式(2)表示的JKM映射到一个联合特征空间F,将样本依据下式进行集中:

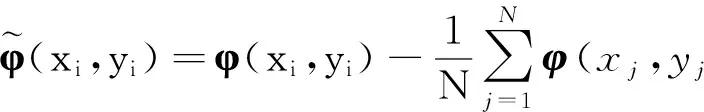
(20)

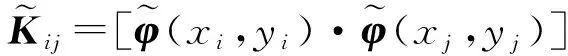
(21)

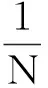
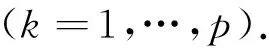
(22)

(23)

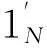
2.4 JKPCA、KPCA和KFDA的联系

下面从理论上讨论JKPCA、KPCA和KFDA三者之间的关系.若式(15)中的K采用常规映射(1),则很容易发现KPCA是JKPCA 的一个特例.对于给定的训练样本,假设有l个类别,第k类有nk个样本,并且设定1=[1,…,1]T∈Rnk,定义如下矩阵:

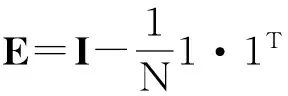
这样,KFDA面向的是如下广义特征值问题:

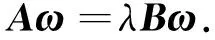
(24)

代入定义的矩阵,式(24)可以转化成

(25)

若使式(15)中的JKPCA的K为K-TD-1CK,则JKPCA就会退化成KFDA.所以不难看出,KPCA和KFDA都是JKPCA的特例.

3 实 验

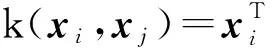
与文献[12-13,16]的工作类似,本文中JKPCA中的联合核定义为两个核映射的张量积,并设定两个核函数为同一形式以方便计算,即J((xi,yi),(xj,yj))=[φ(xi,xj)][φ(yi,yj)].根据核函数的性质有φ(xi,xj)=φ(xi)·φ(xj),则JKM有如下形式:[φ(xi,yi)·φ(xj,yj)]=[φ(xi)·φ(xj)][φ(yi)·φ(yj)].

因此,式(13)中联合核矩阵具有如下形式:

Kij=[φ(xi)·φ(xj)][φ(yi)·φ(yj)]=KxijKyij.

(26)

式中,Kxij=φ(xi)·φ(xj),Kyij=φ(yi)·φ(yj),并分别把线性核、RBF核和多项式核用于Kxij和Kyij.

3.1 在ORL上的实验

ORL数据集总共是来自40个人的图像,每个人有10张不同的姿势和不同的表情变化且尺寸为28×23的图像.图1展示了ORL数据集中来自同一个人的十张图像.针对ORL数据集的实验设置中,使用每个人也就是每一类别中的前5张图作训练,其余的作测试.KPCA和KFDA使用离散的类标号{0,1,2,…}来表示输出空间,很明显,这两个算法关于输出空间的这一设定并不能反映出输出空间的实际结构.而相反地,JKPCA能够在特征提取的过程中考虑到输出空间的结构,因此它比KPCA 和KFDA 得到了更多的先验信息.

图1 ORL数据集示例一个人的10张图像Fig.1 Ten images of one person on ORL data set

在本文的实验中,所有的输入数据xi都来自同一类别,它们有相同的输出y.更具体地,ORL中每个人的第一张图像用作相应的输出.以图1中的人像为例,第一行的5张图用来训练,第二行的用作测试.所有这10张图有共同的输出y,即第一行最左边的图,这样做是因为通常每个图像数据集每一类都会有1或2张标准图像.图2展示了KPCA,KFDA和JKPCA在ORL数据集上变化提取特征维度时的分类正确率.这里要说明的是,基于使用的核不同,共给出了JKPCA的两种形式.图2中,“JKPCA” 表示的是使用了相同的Kxij和Kyij,另一个“JKPCA2”则表示使用了不同的Kxij和Kyij.由图2可以观察到:①JKPCA2在提取特征维度从1到12变化过程中一直保持着比其他算法更高的分类正确率;②JKPCA与KPCA和KFDA相比没有明显的优势,尤其是在低维度上的分类正确率甚至低于二者,与预估不符,出现这种现象可能是由于JKPCA使用相同的Kxij和Kyij造成的.输入空间和输出空间在通常情况下是很不相同的,所以它们对应的映射也不尽相同.而JKPCA2则对输入和输出空间使用了不同的核以与前面描述的情况一致,所以展现出了很好的分类性能.

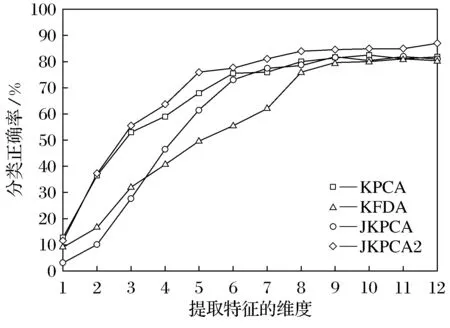
图2 KPCA,KFDA和JKPCA在ORL数据集上变化提取特征维度时的分类正确率

3.2 在Coil-20上的实验

Coil-20是一个从哥伦比亚大学物体图像数据库获取到的实体图像数据集,它包含来自20个实体大小为32×32共1 440张图像.环绕每个实体每5°获取一张图像,共得到72张.图3展示了Coil-20中呈现不同形态的一个实体的图像.针对Coil-20数据集,本文共设计了两个实验.第一个实验是在相同训练集规模下提取不同维度的特征,

其中每个实体选取12张图用来训练,其余的用作测试.第二个实验是从不同规模的训练集中提取固定数目的特征,其中,每个实体用作训练的数量分别是{12,24,36,48,60}.图4给出了相应的实验结果.由图4可以观察到以下两点:①两种情况即不同特征维度和不同训练集规模下,JKPCA2总是比KPCA,KFDA和JKPCA的分类正确率高;②JKPCA2和JKPCA相比于KPCA和KFDA都需要较少或至多相当的训练时间.实验证明了提出的JKPCA不仅提高了分类正确率,并在一定程度上减少了分类器的训练时间,是一种可行的且值得推广的算法.

图3 Coil-20数据集示例一个实体的10张图像Fig.3 Ten images of one object on Coil-20 data set

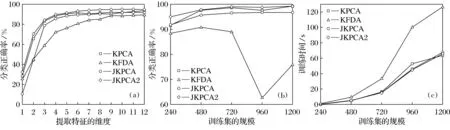
图4 实验结果Fig.4 Experimental result

3.3 在AR上的实验

AR人脸数据集[15]包含126个人超过3 200张的正脸图像.本文使用的是AR的一个子集,包含100个人,每个人20张图,共计2 000张人脸图像.每张图像的尺寸是66×48,分别涉及时间、表情、穿着和光照变化.图5显示了AR数据集中一个人的20张图像,具体的图像细节是:第一行从左数依次为自然表情,微笑,生气,尖叫,戴墨镜,戴墨镜且左侧有光照,戴墨镜且右侧有光照,戴围巾,戴围巾且左侧有光照,戴围巾且右侧有光照.第二行的图像和第一行的情景状况一样,区别是获取图像的时间不同.

图5 AR数据集示例一个人的20张图像Fig.5 Twenty images of one person on AR data set

针对AR数据集,本文总共设计了三个实验.第一个实验针对面部表情的变化,以每个人的第一张图像(如图5中的(a)(k)所示)作训练,其余涉及面部表情的作测试(如图5中的(b)(c)(d)(l)(m)(n)所示).第二个实验针对不同的穿戴,以每个人的第一张图像(如图5中的(a)(k)所示)作训练,有墨镜和围巾的图像(如图5中的(e)(h)(o)(r)所示)作测试.第三个实验针对不同的光照,以每个人的第一张图像(如图5中的(a)(k)所示)作训练,涉及光照的图像(如图5中的(e)(j)(o)(t)所示)作测试.对所有的实验,选择每个人的第一张图像(如图5a所示)表示输出空间y.图6给出了KPCA,KFDA,JKPCA和JKPCA2在变换面部表情、穿着和光照三种训练测试集时不同特征维度下的分类正确率.由图6可以看出,JKPCA和JKPCA2相较于KPCA和KFDA并没有展现出一个很明显的优势,在高维情况下保持了与KPCA,KFDA相当的分类正确率,但同时它提供了一个可以在特征提取过程中同时引入输入和输出空间的新概念.

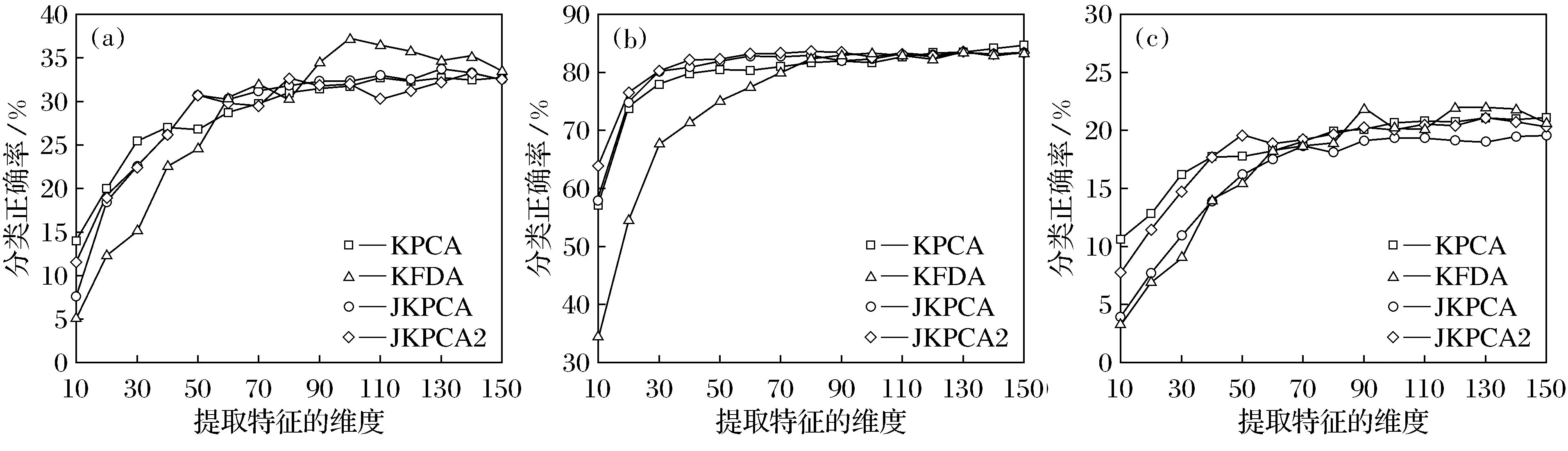
图6 KPCA,KFDA,JKPCA和JKPCA2在变换面部表情、穿着和光照三种训练测试集时不同特征维度下的分类正确率Fig.6 Classification accuracy of KPCA,KFDA,JKPCA and JKPCA2 with varying dimension of the extracted feature vectors on the variation of facial expressions,cover,and both cover and light

4 结 语

本文提出了一种新型的基于核的特征提取方法JKPCA,也是第一次将JKM应用在特征提取过程中.通过与传统的基于核的特征提取方法KPCA和KFDA对比,JKPCA从输入和输出空间引入了更多先验信息.在图像数据集上的实验证明,JKPCA是一种可行有效的方法,它比KPCA和KFDA有更优或者至少相当的分类性能,同时,计算代价也是相当的.今后应进一步探索JKPCA在更复杂输出空间如相互依赖的变量上的有效性.

[1] 张学工.模式识别[M].北京:清华大学出版社,2010.

(Zhang Xuegong.Pattern Recognition[M].Beijing: Tsinghua University Press,2010.)

[2] Jolliffe I T.Principal Component Analysis[M].New York: John Wiley & Sons Ltd.,2005.

[3] Kirby M,Sirovich L.Application of the Karhunen-Loeve Procedure for the Characterization of Human Faces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(1):103-108.

[4] Baudat G,Anouar F.Generalized Discriminant Analysis Using a Kernel Approach[J].Neural Computation,2000,12(10):2385-2404.

[5] 张晓飞,万福才,刘朋.主元分析法(PCA)在图像颜色特征提取中的应用[J].沈阳大学学报,2006,18(5):93-95.

(Zhang Xiaofei,Wan Fucai,Liu Peng.Application of Principal Component Analysis (PCA) Color-Based Feature Extraction of Image[J].Journal of Shenyang University,2006,18(5):93-95.)

[6] Rosipal R,Girolami M.An Expectation-Maximization Approach to Nonlinear Component Analysis[J].Neural Computation,2001,13(3):505-510.

[7] Schölkopf B,Smola A,Müller K R.Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J].Neural Computation,1998,10(5):1299-1319.

[8] Cristianini N,Shawe-Taylor J.An Introduction to Support Vector Machines and other Kernel-Based Learning Methods[M].Cambridge: Cambridge University Press,2000.

[9] Schölkopf B,Smola A.Learning with Kernels[J].Cambridge: The MIT Press,2002:110-146.

[10] Vapnik V.The Nature of Statistical Learning Theory[M].2nd Edition.New York: Springer-Verlag,2000.

[11] Collins M,Duffy N.Convolution Kernels for Natural Language[C]∥ Advances in Neural Information Processing Systems,2001(14):625-632.

[12] Hofmann T,Tsochantaridis I,Altun Y.Learning over Discrete Output Spaces via Joint Kernel Functions[C]∥Advances in Neural Information Processing Systems,Workshop on Kernel Methods,2002.

[13] Tsochantaridis I,Hofmann T,Joachims T,et al.Support Vector Machine Learning for Interdependent and Structured Output Spaces[C]∥Proceedings of the Twenty-first International Conference on Machine Learning.New York: ACM Press,2004:85-103.

[14] Weston J,Chapelle O,Elisseeff A,et al.Kernel Dependency Estimation[C]∥Becker S,Obermayer K.Advances in Neural Information Processing Systems.Cambridge: The MIT Press,2003:873-880.

[15] Martinez A M,Benavente R.The AR Face Database[R].Barcelona: Computer Vision Center (CVC) Technical Report 24,1998.

[16] Weston J,Schölkopf B,Bousquet O,et al.Joint Kernel Maps[C]∥Cabestany J,Prieto A,Sandoval D F.Computational Intelligence and Bioinspired Systems: Eighth International Work-Conference on Artificial Neural Networks,Lecture Notes in Computer Science.Berlin,Heidelberg: Springer-Verlag,2005:176-191.

【责任编辑: 李 艳】

Joint Kernel Principle Component Analysis

WangZhe,MengYun

(Department of Computer Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)

A variant of KPCA called joint kernel principal component analysis (JKPCA) is proposed,which is able to obtain the prior information from both the input and output spaces for the feature extraction processing.Moreover,the joint kernel mapping is applied into feature extraction for the first time.The experimental results validate the feasibility and effectiveness of the proposed JKPCA on image datasets.

kernel principal component analysis (KPCA); joint kernel mapping; feature extraction; kernel-based method

2015-01-14

国家自然科学基金资助项目(61272198).

王 喆(1981-),男,江苏淮安人,华东理工大学副教授,博士.

2095-5456(2015)04-0306-07

TP 181

A