不同地震力偏角下二阶边坡的稳定性分析
李 哲,张 浩,李 立,王 睿,折学森
(1.长安大学 a.特殊地区公路工程教育部重点实验室,b.公路学院,陕西 西安 710064;2.中国船舶重工集团 陕西柴油机重工有限公司,陕西 咸阳 713105;3.延长石油集团 天然气液化厂,陕西 延安 716000)
不同地震力偏角下二阶边坡的稳定性分析
李 哲1a,1b,张 浩1b,李 立2,王 睿3,折学森1b
(1.长安大学 a.特殊地区公路工程教育部重点实验室,b.公路学院,陕西 西安 710064;2.中国船舶重工集团 陕西柴油机重工有限公司,陕西 咸阳 713105;3.延长石油集团 天然气液化厂,陕西 延安 716000)
针对边坡在地震力作用下的稳定性问题,在毕肖普法中考虑受地震力影响产生切向力和竖向力,建立了线性二阶边坡受力模型,对不同地震力偏角范围内边坡安全系数的计算公式进行了推导.开发出工程计算软件进行迭代计算,分析了边坡台阶宽度比、坡率比以及地震力偏角的变化对边坡稳定性的影响,为边坡抗震设计提供了重要的参考依据.
边坡稳定; 地震力偏角; 安全系数; 边坡抗震
历次大地震的经验表明,山区公路高边坡抗震能力及防灾减灾措施已成为当前需要认真研究的重大课题[1].地震后大量高边坡的垮塌不仅严重影响了救援交通,也对灾后公路交通的恢复重建带来很多技术难题[2].针对地震对公路高边坡产生的破坏,如何在今后的新建公路设计中进行计算分析,采取相应的技术对策,安全可靠地评价,选定经济合理的边坡抗震设计方案,十分需要开展系统深入的研究[3-17].本文对震区公路二阶边坡破坏进行了理论分析与研究.
1 二阶边坡力学分析模型
将二阶高边坡破坏问题看作平面上边坡坡体的应变问题,并且假定此类边坡土体均质,边坡坡顶水平投影平行于边坡坡肩线的垂直裂隙[3-6],这样就可以按照如图1所示的二阶高边坡破坏模型进行理论研究[14,16].
如图1所示,由对应的不确定性参数u、v及α可以得出圆弧滑动面的圆心坐标O(ξ,η)及半径R.由几何关系得:
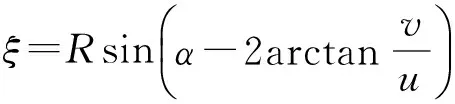
(1)
(2)
(3)
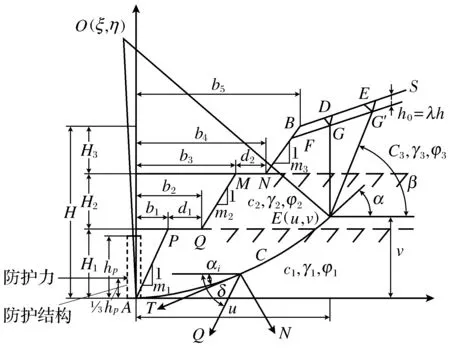
图1 二阶边坡支护结构抗震模型Fig.1 The second-order slope supporting seismic model
设边坡失稳时滑动力矩和抗滑力矩分别为MS、Mr,其中,MS及Mr分别为待定参数u、v、α及β的函数,则边坡的安全系数可表示为
(4)
对式(4)的求解,只需推导得出滑动力矩MS及抗滑力矩Mr的计算公式即可,然后可以用数学迭代法求出最小安全系数Kmin.对上面的线性坡型,下面将给出MS(u,v,α,β)和Mr(u,v,α,β)的计算公式[17].
2 二阶平台边坡在地震作用下安全系数的计算公式的推导
对于如图1所示的均匀土、二阶平台坡型的边坡,坡体以台阶为界分为三种土层.坡面及坡顶面的方程分别如下[5].
AP坡面
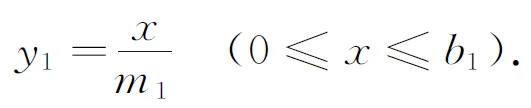
(5)
坡面
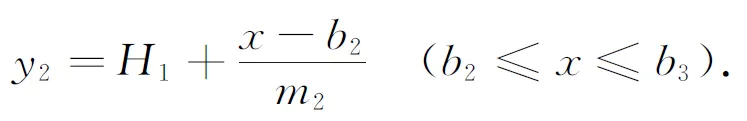
(6)
坡面
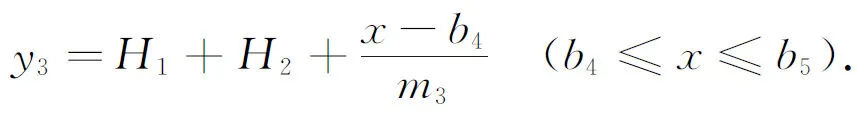
(7)
坡顶面
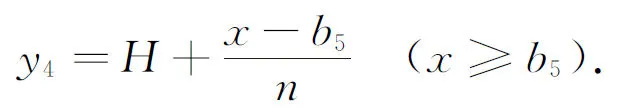
(8)
其中:b1=m1H1,b2=b1+d1,b3=b2+m2H2,b4=b3+d2,b5=b4+m3H3.
由于坡体由三种土层组成,因此,需根据滑动面上E点可能在不同土层中的情况,分别推导滑动力矩和抗滑力矩的计算公式[14].
(1) 当E点位于土层Ⅰ中(v>H1+H2)时,分以下几种情况.
① 当地震角δ在(270°+αi)~0和0~αi时,计算公式如下.
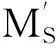
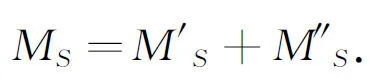
(9)
和M″S的计算方法是

(10)
(11)

b.求解抗滑力矩Mr的计算公式.滑动坡体上摩擦力、黏结力、地震作用力以及防护力P产生的力矩总和为抗滑力矩,即
(12)
式中:P为防护力的大小;hp为支护结构的高度.
(13)
式中
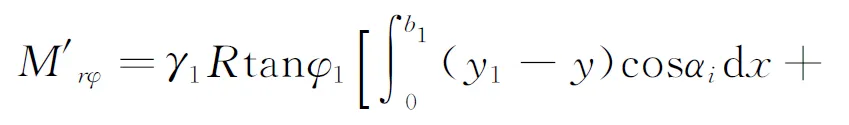
(14)
(15)
式中
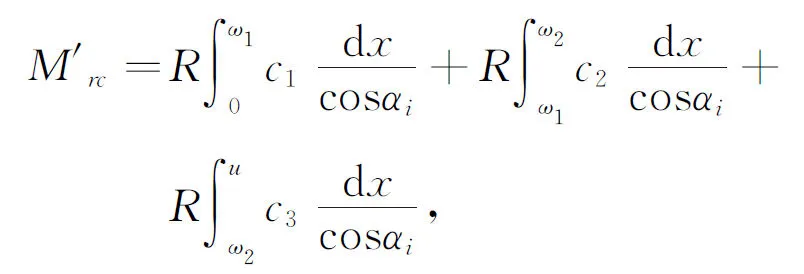
(16)
(17)
其中:c1,c2,c3分别为ACE弧面上三种土层的黏结力;c30为EG斜面上的黏结力.
(18)
(19)
因此,当地震角δ在(270°+αi)~0和0~αi时,公路高边坡稳定性系数为
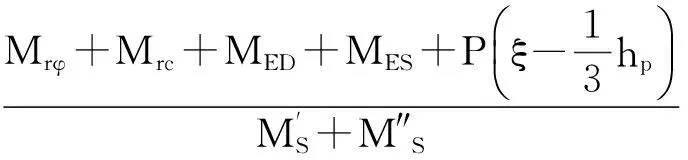
(20)
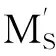
② 当地震角δ在αi~(90°+αi)时,计算地震角δ在(270°+αi)~0和0~αi时的式中MES变为负值,因此,安全系数可以如下表示:
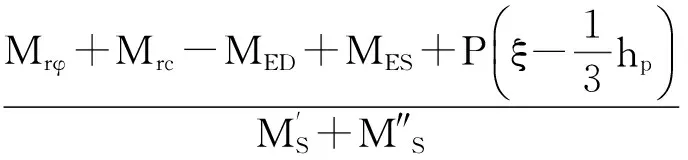
(21)
③ 当地震角δ在(90°+αi)~(180°+αi)时,地震力产生的力矩MES为滑动力矩,且地震力分解法方向产生的抗滑力矩仍为负值,则安全系数就变换为
(22)
④ 当地震角δ在(180°+αi)~(270°+αi)时,地震力产生的力矩MES为滑动力矩,且地震力分解法方向产生的抗滑力矩为正值,则安全系数就变换为
(23)
(2) 当E点位于土层Ⅱ中(H1 由表1及图2可见,在其他条件一定的情况下,当平均坡率小于或等于1.0,台阶宽度比d1/d2在1.5附近时,安全系数最小,边坡最不安全;当平均坡率达到1.2时,台阶宽度的比值对边坡的安全性影响不明显. 表1 边坡安全系数随平均坡率及台阶宽度比d1/d2变化的计算结果Table1 The results of the safety factor of slope varied with average slope rate and width ratio d1/d2 图2 边坡安全系数随平均坡率及台阶宽度比d1/d2变化的计算曲线Fig.2 Calculated curve of slope safety factor of slope varied with average slope rate and width ratio d1/d2 图3 边坡安全系数随平均坡率及坡率比m2/m3变化的计算曲线Fig.3 Calculated curve of slope safety factor of slope varied with average slope rate and slope rate ratio m2/m3 由表2及图3可见,平均坡率为0.8,加速度为0.15g时,坡率比的变化对安全系数的影响较大;平均坡率为1.0,加速度为0.10g时,坡率比的变化对安全系数的影响较大;在平均坡率等于1.2时,三种加速度情况下的坡率比对边坡的安全系数影响都不明显. 表2 边坡安全系数随平均坡率及坡率比m2/m3变化的计算结果Table2 The results of the safety factor of slope varied with average slope rate and slope rate ratio m2/m3 5.1 工程简介 如图4所示,该处边坡起讫桩号为K318+950~K319+050,坡层岩性分布为:表层分布10 m的含少量砾石的粉质黏土,γ=21 kN/m3,c=39 kPa,φ=24°;中部为12 m厚的碎石土,γ=28 kN/m3,c=41 kPa,φ=27°;下部为13 m的强风化志留系千枚岩,存在构造破碎带,为潜在的滑动面,γ=30 kN/m3,c=57 kPa,φ=36°. 图4 K318+950~K319+050处边坡施工照片Fig.4 Slope Construction location in K318+950~K319+050 5.2 稳定性验算 图5所示为简化坡型,表3给出了该边坡的岩土性质参数,分别采用本文的方法、拟静力法对其稳定性进行计算分析,得出的安全系数值如表4所示. 图5 计算分析中采用的简化坡型Fig.5 Simplified slope used in calculation 从表4可以得出,当不考虑地震作用时,边坡处于稳定状态;地震作用下,未加防护时采用拟静力法计算,当加速度为0.05g,0.1g时,安全系数分别为0.917,0.884,自然状况下边坡处于不稳定状态[14].相应地,从表4中的计算可以看出,当地震入射角是45°时,安全系数分别为1.395,1.887;当地震入射角为135°时,可得安全系数最小值分别为0.948,0.816.在不加任何防护的情况下,依照最不利原则,本边坡处于不稳定状态.但当所加的防护力P为3 000 kN,作用点高度距坡脚3 m时,边坡最小安全系数为1.223,边坡处于稳定状况.为了保证边坡的稳定性,必须采用相应的防护措施,本文以计算所得的防护力及作用点高度为指导,采用混凝土骨架的形式对边坡进行防护. 表3 岩土层的物理力学性质指标Table3 Physical mechanical properties index of rock layers 表4 不同方法时安全系数的计算结果Table4 Calculation results of stability coefficient with different methods 5.3 工后观测 十天后高速公路K318+800~K319+880处边坡路基右侧边坡防护工程完工后,通过两年的观测表明,整体稳定性良好,如图6所示. 图6 K318+800~K319+880处边坡后期效果Fig.6 Post effects of slope location in K318+800~K319+880 (1) 在其他条件一定的情况下,当平均坡率小于或等于1.0,台阶宽度比d1/d2在1.5附近时,安全系数最小,边坡最不安全;当平均坡率达到1.2时,台阶宽度的比值对边坡的安全性影响不明显. (2) 平均坡率为0.8,加速度为0.15g时,坡率比的变化对安全系数的影响较大;平均坡率为1.0,加速度为0.10g时,坡率比的变化对安全系数的影响较大;在平均坡率等于1.2时,三种加速度情况下的坡率比对边坡的安全系数影响都不明显. (3) 当不考虑地震作用时,边坡处于稳定状态;地震作用下,采用拟静力法计算,当加速度为0.05g,0.1g时,安全系数分别为0.917,0.884,因此,地震时自然状况下边坡稳定性较差.根据本文的方法,通过编制VB程序迭代计算,得出地震入射角从0°~360°变化,相应的安全系数呈先减小后增大的变化趋势,地震入射角为135°时,可得安全系数最小值分别为0.948,0.816,按照最不利原则,地震时在不加任何防护的情况下该边坡已处于不稳定状态,而运用拟静力法得到的结果是边坡处于安全状态.现在在抗震设计中较多运用拟静力法将180°的地震力偏角作为最危险角度进行设计,但是从本文的研究可以看出,在其他因素确定时,最危险的地震力偏角并不是180°. [1] 刘立平,雷尊宇,周富春.地震边坡稳定分析方法综述[J].重庆交通学院学报,2001,20(3):83-88. (Liu Liping,Lei Zunyu,Zhou Fuchun.The Evaluation of Seismic Slope Stability Analysis Methods[J].Journal of Chongqing Jiaotong University,2001,20(3):83-88.) [2] 张希然,谢锴,康晓茜.浅谈吉怀高速公路上边坡生态防护[J].公路工程,2011,36(3):166-168,178. (Zhang Xiran,Xie Kai,Kang Xiaoxi.Jishou-huaihua to Discuss on Highway Slope Ecological Protection[J].Highway Engineering,2011,36(3):166-168,178.) [3] Newmark N M.Effects of Earthquakes on Dams and Embankments[J].Geotechnique,1965,15(2):139-160. [4] 祁生文,伍法权,刘春玲,等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报,2004,23(16):2792-2797. (Qi Shengwen,Wu Faquan,Liu Chunling,et al.Engineering Geology Analysis on Stability of Slope under Earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(16):2792-2797.) [5] 郝哲,陈殿强,侯永莉.沈阳地铁隧道开挖过程稳定性分析[J].沈阳大学学报:自然科学版,2012,24(4):78-81,86. (Hao Zhe,Chen Dianqiang,Hou Yongli.Stability Analysis on Excavation Process of Shenyang Metro Tunnel[J].Journal of Shenyang University: Natural Science,2012,24(4):78-81,86.) [6] 徐茂其.地貌要素对自然边坡稳定性的影响[C]∥自然边坡稳定性分析暨华蓥山边坡变形趋势研讨会论文集.北京:地震出版社,1993:118-123. (Xu Maoqi.Impact Landform Elements of the Natural Slope Stability[C]∥Natural Slope Stability Analysis and Deformation Huayingshan Symposium.Beijing: Seismological Press,1993:118-123.) [7] 蒋溥,戴丽思.工程地震学概论[M].北京:地震出版社,1993:23-24. (Jiang Pu,Dai Lisi.Engineering Seismology[M].Beijing: Seismological Press,1993:23-24.) [8] 汤建良.高烈度地震区公路隧道衬砌刚度对地震反应影响的研究[J].公路工程,2013,38(2):190-192,201. (Tang Jianliang.Research of the Seismic Response on Lining Stiffness of Highway Tunnel in High-Intensity Seismic Region[J].Highway Engineering,2013,38(2):190-192,201.) [9] 于翔,钱七虎,赵跃堂,等.地铁工程结构破坏的竖向地震力影响分析[J].解放军理工大学学报:自然科学版,2001,2(3):75-77. (Yu Xiang,Qian Qihu,Zhao Yuetang,et al.Analysis of Vertical Earthquake Influence on Damage to Subway Structures[J].Journal of PLA University of Science and Technology: Natural Science Edition,2001,2(3):75-77.) [10] 姜彤.边坡在地震力作用下的加卸载响应规律与非线性稳定分析[D].北京: 中国地震局地质研究所,2004:23-26. (Jiang Tong.Load-Unload Responses of Slopes under Seismic Load and Nonlinear Stability Analysis[D].Beijing: Institute of Geology,China Earthquake Administration,2004:23-26.) [11] 赵学勐,陈运理.考虑垂直裂隙影响的均质黄土挖方边坡稳定性分析[J].土木工程学报,1981(1):43-49. (Zhao Xuemeng,Chen Yunli.Stability Analysis of Cut Slopes in Uniform Loess[J].China Civil Engineering Journal,1981(1):43-49.) [12] 叶万军,折学森,陈志新,等.基于可靠度理论的黄土高边坡优化设计[J].地球科学与环境学报,2005,27(2):82-85. (Ye Wanjun,She Xuesen,Chen Zhixin,et al.Optional Design of High Loess Slope in Highway Based on Reliability Method[J].Journal of Earth Sciences and Environment,2005,27(2):82-85.) [13] JTJ 004—89公路工程抗震设计规范[S].北京: 人民交通出版社,1999:85-89. (JTJ 004—89 Highway Engineering Seismic Design Code[S].Beijing: China Communications Press,1999:85-89.) [14] 张景焘,杨鹏,胡玉娇,等.基于不同地震力偏角的一阶边坡稳定性分析[J].宁夏大学学报:自然科学版,2014,35(2):130-135. (Zhang Jingtao,Yang Peng,Hu Yujiao,et al.The First Slope Stability Analysis Based on Different Seismic Force Angle[J].Journal of Ningxia University: Natural Science Edition,2014,35(2):130-135.) [15] Morgenstern N R,Price V.The Analysis of the Stability of General Slip Surface[J].Geotechnique,1965,15(1):79-93. [16] 杨鹏,张景焘,周丹,等.基于不同地震力偏角的边坡稳定性分析[J].水利与建筑工程学报,2014,12(2):58-61,66. (Yang Peng,Zhang Jingtao,Zhou Dan,et al.Slope Stability Analysis Based on Different Seismic Force Angle[J].Journal of Water Resources and Architectural Engineering,2014,12(2):58-61,66.) [17] 郑颖人,叶海林,黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报,2009,28(8):1714-1723. (Zheng Yingren,Ye Hailin,Huang Runqiu.Analysis and Discussion of Failure Mechanism and Fracture Surface of Slope under Earthquakes[J].China Journal of Rock Mechanics and Engineering,2009,28(8):1714-1723.) 【责任编辑: 李 艳】 Stability of the Second-Order Slope Based on Different Seismic Force Angle LiZhe1a,1b,ZhangHao1b,LiLi2,WangRui3,SheXuesen1b (1.a.Key Lab of Highway Engineering in Special Region (Ministry of Education),b.College of Highway Engineering,Chang’an University,Xi’an 710064,China; 2.Shaanxi Deisel Engine Heavy Industry Co.,Ltd.,China Shipbuilding Industry Corporation,Xianyang 713105,China; 3.Natural Gas Liquefaction Plant,Shaanxi Yanchang Petroleum (group) Co.,Ltd.,Yan’an 716000,China) Aiming at the problem of the slope stability under the seismic force,the vertical force and horizontal force formed in the earthquake are considered in Bishop Method.The stress model for the second-order slope was built.The equation of slope safety factors was derived.The engineering calculation software was developed to make iterative calculation.The influence of variation of width ratio,slope rate ratio and seismic force angle on slope stability were analyzed,which provides important reference basis for the seismic design of slope. slope stability; seismic force angle; safety factor; slope seismic 2015-03-08 交通部科技项目资助项目(2008353361420); 高等学校博士学科点专项科研基金资助项目(20110205110003). 李 哲(1989-),男,陕西咸阳人,长安大学硕士研究生; 折学森(1956-),男,陕西绥德人,长安大学教授,博士生导师. 2095-5456(2015)04-0324-07 U 416 A3 台阶的宽度比d1/d2对边坡稳定性的影响
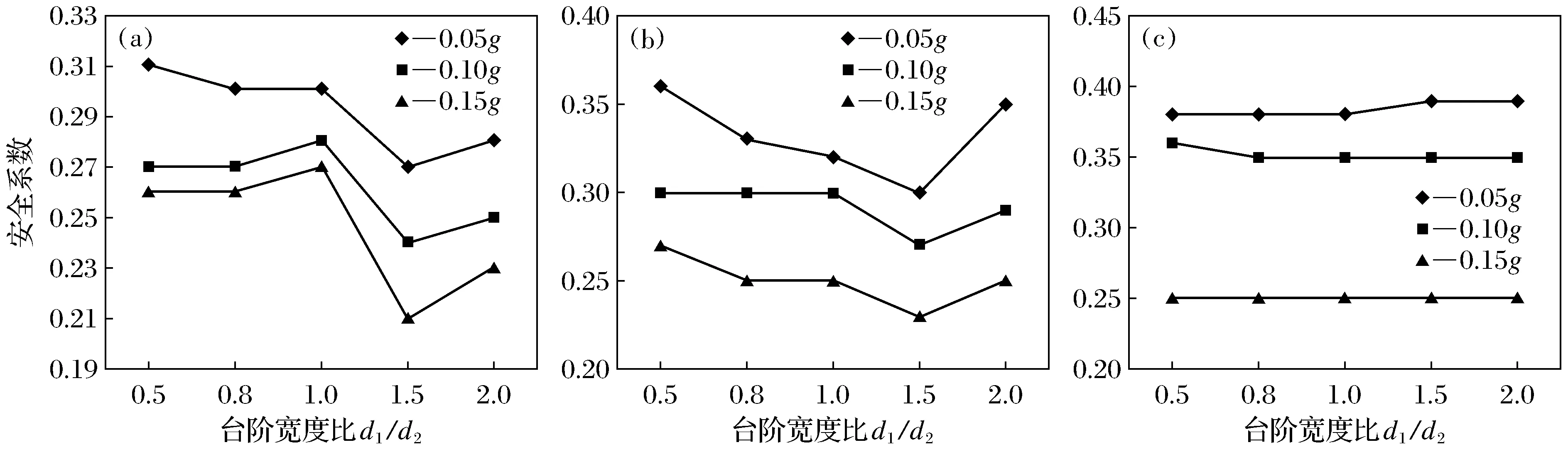
4 边坡的坡率比m2/m3对安全系数的影响
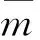
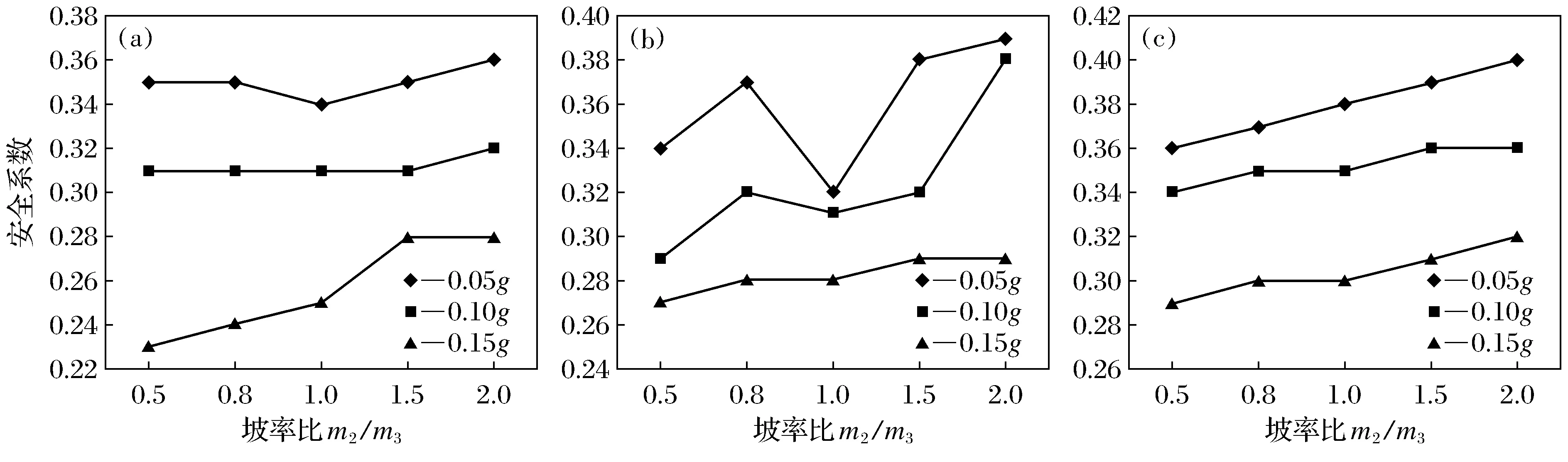
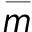
5 工程实例分析





6 结 语

