基于异步次梯度法的LR算法及其在多阶段HFSP的应用

轩 华， 李 冰

(郑州大学 管理工程学院，河南 郑州 450001)



基于异步次梯度法的LR算法及其在多阶段HFSP的应用

轩 华， 李 冰

(郑州大学 管理工程学院，河南 郑州 450001)

为降低求解复杂度和缩短计算时间，针对多阶段混合流水车间总加权完成时间问题，提出了一种结合异步次梯度法的改进拉格朗日松弛算法。建立综合考虑有限等待时间和工件释放时间的整数规划数学模型，将异步次梯度法嵌入到拉格朗日松弛算法中，从而通过近似求解拉格朗日松弛问题得到一个合理的异步次梯度方向，沿此方向进行搜索，逐渐降低到最优点的距离。通过仿真实验，验证了所提算法的有效性。对比所提算法与传统的基于次梯度法的拉格朗日松弛算法，结果表明，就综合解的质量和计算效率而言，所提算法能在较短的计算时间内获得更好的近优解，尤其是对大规模问题。

系统工程；异步次梯度法；拉格朗日松弛算法；多阶段混合流水车间问题；总加权完成时间

0 引言

混合流水车间问题(HFSP)所处的制造环境一般可描述为：一组工件L={1, 2, …,M}按照相同的加工顺序依次经过G个加工阶段进行加工，每个阶段g由mg台同构并行机组成，且至少有一个加工阶段的mg> 1；每个工件在每个阶段至多在一台同构机上加工；每台机器任何时间至多只能加工一个工件而每个工件在任何时间也只能在一台机器上加工。因此，HFSP要解决的问题是：将工件分配到机器上且确定在每个加工阶段的机器上工件的调度，同时还要最优化某个给定的目标函数[1，2]。

本文研究了一类较为复杂的HFSP，该问题区别于一般的HFSP：

·工件b在相邻两个加工阶段之间有等待时间限制；

·每个工件在时刻Fb(Fb≥1)才能用于加工；

·相邻加工阶段间的运输时间不可忽略。

Gupta证明了两阶段HFSP是NP-hard，即使一个加工阶段只有一台机器。因此，本文所研究的更复杂的HFSP也是NP-hard[3]，这使得探讨求解这类问题的近似算法显得尤为重要。

拉格朗日松弛(LR)算法作为一种基于最优化的近似算法，其基本思想是分解和协调，对于实际调度问题通过合理的设计该算法可在合理的计算时间内获得具有可量化质量的近优解[4]。传统的LR算法通过引入拉格朗日乘子向量松弛机器能力约束，进而将形成的松弛问题分解为多个工件级子问题，利用动态规划最优求解这些子问题，然后利用次梯度法更新乘子，利用启发式将子问题的解转换为原问题的可行解。重复上述过程直到满足一定的停止条件。

然而，当实际问题规模较大时，利用动态规划最优求解拉格朗日子问题的计算复杂度也随之增大，这使得求解相当耗时。因此，本文在LR算法中引入了异步次梯度法，该方法是代理次梯度法的一种特殊情况[5]，它要求每次迭代最优求解一个拉格朗日子问题从而节约了计算时间，目的在于在较短的计算时间内得到大规模问题的较好解。

基于代理次梯度法的LR已被用于求解不同的生产调度问题。文献[4,6,7]利用结合代理次梯度法的LR算法求解了单件车间调度，以提高准时传送和降低在制品库存。就总加权完成时间问题，文献[8]研究了带有限中间存储的实时HFSP；文献[9]则考虑了可重入HFSP。文献[10]求解了带顺序相关调整影响(时间和费用)的HFSP，目标是降低在制品库存和调整费用。文献[11]求解了炼钢-连铸生产调度问题，该过程可视为HFS结构，目标是减少断浇、降低炉次在加工阶段间的等待时间和满足准时传送要求。

就目前所查阅的资料来看，近年来基于代理次梯度法的LR在HFSP的优化研究较少，且既有研究缺乏对有限等待等实际生产特征的探讨。而对于不同的生产调度问题有必要研究算法的具体实现方式以得到满意解。因此，以总加权完成时间为目标，本文研究了求解带等待考虑的HFSP的嵌入异步次梯度法的LR的有效性，扩展了LR算法理论及其应用。

1 多阶段HFSP描述

本文所研究的HFSP是在G个阶段的同构并行机上按照相同的加工顺序调度M个工件，目标是最小化总加权完成时间以降低在制品库存。工件在相邻加工阶段间的等待时间不允许超过等待上限。假定每个操作不允许中断，每个工件在时刻Fb才能开始加工，运输时间不可忽略。

1.1 符号说明

已知参数：M为总工件数；G为总阶段数；mg为阶段g可利用的机器数；Obg为工件b(b=1,2,…,M)在阶段g(g=1,2,…,G)的加工时间;Fb为工件b的释放时间;Gg,g+1为阶段g和g+1的运输时间;Ubg工件b在相邻阶段g和g+1间的等待上限;K为总计划时间水平。

决策变量：Cbg为工件b在阶段g的完工时间;Xbgt为0-1变量，若工件b在时刻t正在阶段g上加工，则其值为1，否则为0.g=1,2,…,G;b=1,2,…,M;t=1,2,…,K。

1.2 整数规划模型

(1)

满足

Cbg≤Cb,g+1-Obg-Dg,g+1,b=1,…,M;g=1,…,G-1

(2)

(3)

Cbg-Obg+1≤t+K(1-Xbgt),b=1,…,M;g=1,…,G;t=1,…,K

(4)

tXbgt≤Cbg,b=1,…,M;g=1,…,G;t=1,…,K

(5)

Cb,g+1-Ob,g+1-Dg,g+1-Cbg≤Ubg,b=1,…,M;g=1,…,G-1

(6)

(7)

Cb1-Ob1+1≥Fb,b=1,…,M

(8)

Xgbt∈{0, 1},b=1,…,M;g=1,…,G;t=1,…,K

(9)

Cbg∈{1,2, …,K},b=1,…,M;g=1,…,G

(10)

文献[12]也建立了带有限等待HFSP的数学模型，但是本文的目标是满足上述所有约束的条件下最小化总加权完成时间，而[12]则还考虑了等待惩罚。

约束(2)表示了一个工件在加工阶段间的操作优先级；约束(3)～(5)定义了每个工件在加工阶段上占用机器的时间间隔；约束(6)表示了工件在阶段g完成加工且送达阶段g+1之后的等待时间不能超过等待上限；约束(7)说明了所有机器需求都要满足当时可利用的机器数；约束(8)说明了每个工件只有在其到达生产系统始端才能开始加工；约束(9)～(10)定义了变量的取值范围。

2 求解框架

基于工件分解策略，将机器能力约束通过引入拉格朗日乘子松弛到目标函数中，松弛能力约束的目的在于使得松弛后的问题可分解为多个相对容易求解的工件级子问题。

2.1 松弛和分解

引入拉格朗日乘子向量ψ(其分量为{ψgt})，将约束(7)松弛到目标函数中，形成拉格朗日松弛问题：

满足约束(2)～(6),(8)～(10)和

ψgt≥0,g=1,2,…,G;t=1,2,…,K

(11)

则拉格朗日对偶问题是

(12)

满足约束(2)～(6),(8)～(11)。

给定{ψgt}，工件b的工件级子问题Hb(ψ)为：

(13)

满足约束(2) ～(6), (8)～(11)。

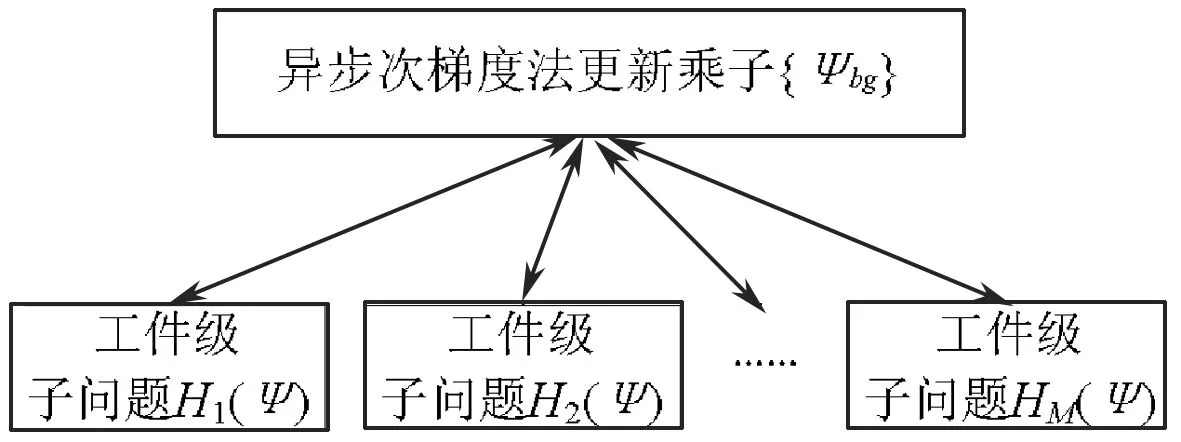
图1 两级分解-协调结构

2.2 分解和协调

图1显示了LR算法的两级分解-协调结构。在“低级”，已知乘子{ψgt}的条件下求解M个工件级子问题；在“高级”，基于约束违反的程度更新乘子{ψgt}，然后根据子问题的解设计启发式将其转换成可行解，直到迭代过程结束[4]。

所设计的LR算法与传统LR算法不同之处在于所设计的算法在每次迭代近似求解子问题以及利用了异步次梯度法[5]在“高级”更新乘子。

3 子问题的近似求解和可行解的构造

3.1 子问题

给定某工件B和乘子{ψgt}，后向动态规划最优求解的递归关系式为：

(14)

(15)

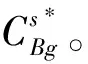
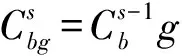
3.2 可行解的构造

基于上述得到的松弛问题的解，对每个阶段g，按照工件在该阶段的开始时间的增序排列，然后依次将其分配到可利用的机器上，若相邻加工阶段间的等待时间超过Ubg，则延迟该工件在阶段g-1的开始时间直到满足等待时间约束。

4 对偶问题

传统的次梯度法要求每次迭代最优求解所有拉格朗日子问题以得到次梯度方向，因此当问题规模较大时，松弛问题的求解较为复杂且费时。为此，设计了异步次梯度法[5]以减少每次迭代所耗费的求解时间，它在每个子问题求解后即可更新乘子。

代理对偶函数定义为：

(16)

则代理次梯度定义为:

(17)

异步次梯度法的执行过程如下：

步骤0 初始化ψ0，最小化所有子问题得到X0，即

计算对偶费用和次梯度，沿次梯度方向更新乘子。令子问题标号p= 1。

步骤1 已知第s次迭代的ψs，最优求解第p个子问题，同时保持其它子问题的解不变，根据式(16)和(17)分别计算代理对偶费用和代理次梯度。

步骤2 由上步得到的ψs和Xs，更新拉格朗日乘子：

(18)

其中步长α定义为：

(19)

步骤3 令p=p+1，如果p>M，则重设p=1。

步骤4 如果CPU时间达到某个限定值或代理对偶间隙小于很小的数，程序停止，否则返回步骤1。

5 仿真实验

利用C语言在PC(2.10GHz CPU)执行所设计的算法，仿真实验将该算法与传统的基于次梯度法的LR进行了比较。首先，对中小规模问题进行测试说明两种算法的有效性；然后比较实际大规模问题的运行结果以估计实际规模问题的性能。

所测试问题的最大规模是200个工件，4个阶段，5台并行机。对于每组{M,G,mg}随机产生10个实例；在每个实例中，每个工件的数据随机产生如下：权重和加工时间满足均匀分布U[1,10]，释放时间满足均匀分布U[1,5]。相邻加工阶段间的运输时间满足均匀分布U[1,3]。等待时间取为5, 15。总时间水平设为所有加工时间之和。算法在90秒后终止。

用LR-ISG表示基于异步次梯度法的LR，用LR-SG表示传统的基于次梯度法的LR。以对偶间隙和迭代数来衡量两种算法的性能指标。SDG定义为代理对偶间隙(%)，其值等于(UB-SLB)/SLB×100%，DG为真正对偶间隙，由(UB-LB)/LB×100%计算得到，IN表示迭代数，这里，UB表示可行费用，即原问题的上界；LB表示对偶费用，即下界；SLB为代理对偶费用。

5.1 实例1

本节测试了40和80个工件的情况，计算结果显示在表1～2中，表中的结果(除最后一行外)为同一规模的10组实例的平均值。从表中可得知：

(1)对于40个工件的情况，当U=5和15时由LR-ISG得到的平均对偶间隙分别为2.64%和3.09%，LR-SG得到的分别为2.97%和3.26%，因此，所提算法比传统LR得到的对偶间隙平均降低0.33%和0.17%。

(2)对于80个工件的情况，当U=5和15时由LR-ISG得到的平均对偶间隙分别为5.22%和6.04%，LR-SG得到的分别为5.46%和7.99%，因此，所提算法比传统LR得到的对偶间隙平均降低0.24%和1.95%。

(3)在相同的计算时间内，LR-ISG执行的迭代数是LR-SG的几十倍，这是由于LR-ISG每次迭代只最优求解一个子问题所耗费的计算时间比最优求解所有子问题要少得多。

(4)当U=5和15时，LR-ISG的代理对偶间隙与真正对偶间隙的偏差分别为0.04%和0.05%(对于40个工件)，0.38%和0.49%(对于80个工件)，即LR-ISG得到的代理对偶间隙和真正对偶间隙相差不大。

综上可知，对中小规模问题，这两种算法都能在较短的计算时间(90s)内得到很好的近优解，且所提出的LR算法表现略佳。

表1 M=40的测试结果

表2 M=80的测试结果

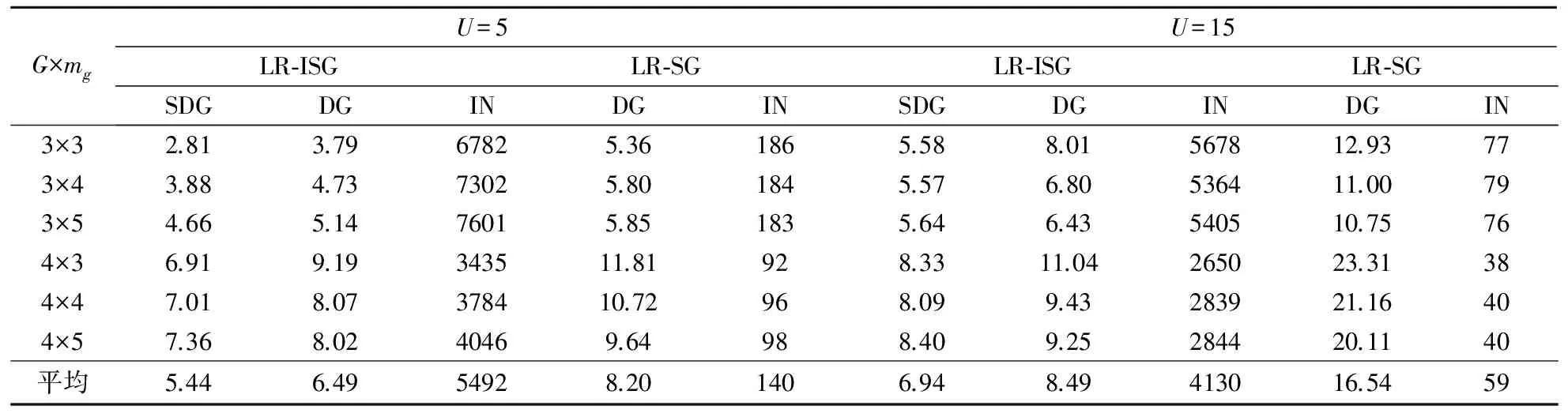
表3 M=120的测试结果

表4 M=150的测试结果

表5 M=200的测试结果

5.2 实例2

本节测试的工件数取自{120,150,200}，测试结果如表3～5所示，从表中结果可得到如下结论：

(1)当U=5时，对于120个工件，150个工件和200个工件的情况，LR-ISG分别在在5492次，3732次和1939次迭代得到的平均代理对偶间隙为5.44%，5.25%，5.34%；真正的对偶间隙分别为6.49%，6.70%，7.83%。由LR-SG分别在140次，90次和51次迭代得到的对偶间隙为8.20%，10.86%，18.79%。因此，LR-ISG的对偶间隙比LR-SG降低1.71%，4.16%，10.96%。

(2)当U=15时，对于120个工件，150个工件和200个工件的情况，LR-ISG分别在在4130次，2900次和1860次迭代得到的平均代理对偶间隙为6.94%，7.32%，8.63%；真正的对偶间隙分别为8.49%，9.60%，13.56%。由LR-SG分别在59次，36次和18次迭代得到的对偶间隙为16.54%，27.42%，51.97%。因此，LR-ISG的对偶间隙比LR-SG降低8.05%，17.82%，38.41%。

(3)当U=5和15时，LR-ISG的代理对偶间隙与真正对偶间隙的偏差分别为1.05%和1.55%(对于120个工件)，1.45%和2.28%(对于150个工件)，2.49%和4.93%(对于200个工件)，即随着问题规模的增大，LR-ISG得到的代理对偶间隙和真正对偶间隙相差也越大。

综上可知，LR-ISG对于大规模问题能在较短的计算时间(90s)内得到很好的近优解，在解的质量和计算效率方面，LR-ISG明显优于LR-SG。

6 结束语

本文针对考虑等待的HFSP设计了嵌入异步次梯度法的改进LR算法，目标是最小化总加权完成时间。通过松弛问题的近似求解简化每次迭代的计算复杂度和所需的计算时间，进而得到一个合理的异步次梯度方向以搜索更好的解。仿真实验结果表明在求解小到大规模问题时所提出的算法能够在较短的计算时间内获得很好的近优解，尤其对于实际大规模问题，它的性能明显优于传统LR。进一步的工作可将该方法推广到具有其它生产特征的复杂生产调度问题中。

[1] Gicquel C, Hege L, Minoux M, van Canneyt W. A discrete time exact solution approach for a complex hybrid flow-shop scheduling problem with limited constraints[J]. Computers & Operations Research, 2012, 39(3): 629- 636.

[2] Niu Q, Zhou T, Fei M, Wang B. An efficient quantum immune algorithm to minimize mean flow time for hybrid flow shop problems[J]. Mathematics and Computers in Simulation, 2012, 84: 1-25.

[3] Gupta J N D. Two-stage hybrid flowhsop scheduling problem[J]. Journal of the Operational Research Society, 1988, 39: 359-364.

[4] Chen H X, Luh P B. An alternative framework to Lagrangian relaxation approach for job shop scheduling[J]. European Journal of Operational Research, 2003, 149(3): 499-512.

[5] Zhao X, Luh P B, Wang J. Surrogate gradient algorithm for lagrangian relaxation[J]. Journal of Optimization Theory and Application, 1999, 100(3): 699-712.

[6] Sun T, Luh P B, Liu M. Lagrangian Relaxation for complex job shop scheduling[C]. Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, Florida, May 15-19, 2006, 1432-1437.

[7] Wang J, Luh P B, Zhao X, Wang J. An optimization-based algorithm for job shop scheduling[J]. SADHANA(a Journal of Indian Academy of Sciences on Competitive Manufacturing Systems), 1997, 22: 241-256.

[8] Tang L, Xuan H. Lagrangian relaxation algorithms for real-time hybrid flowshop scheduling with finite intermediate buffers[J]. Journal of the Operational Research Society, 2006, 57(3): 316-324.

[9] Jiang S, Tang L. Lagrangian Relaxation algorithms for re-entrant hybrid flowshop scheduling[C]. International Conference on Information Management, Innovation Management and Industrial Engineering, Taipei, December 19-21, 2008, 78- 81.

[10] Liu C Y, Chang SC. Scheduling flexible flow shops with sequence-dependent setup effects[J] IEEE Transactions on Robotics and Automation, 2000, 16(4): 408- 419.

[11] Sun L, Chai T, Luh P B. Scheduling of steel-making and continuous casting system using the surrogate subgradient algorithm for Lagrangian relaxation[C]. 6th annual IEEE Conference on Automation Science and Engineering, Toronto, Ontario, Canada, August 21-24, 2010, 885- 890.

[12] 轩华.带有限等待的动态HFS调度的拉格朗日松弛算法[J].工业工程与管理,2013,18(3):24-29.

Lagrangian Relaxation Using Interleaved Subgradient Method and Its Application for Multi-stage HFSP

XUAN Hua, LI Bing

(SchoolofManagementEngineering,ZhengzhouUniversity,Zhengzhou450001,China)

In order to reduce solution complexity and computation time, an improved Lagrangian relaxation algorithm combined with an interleaved subgradient method is presented to solve total weighted completion time problem of multi-stage hybrid flowshop. An integer programming model is firstly formulated for HFSP considering finite waiting time and job release time. An interleaved subgradient method is then introduced into Lagrangian relaxation which requires approximately solving Lagrangian relaxation problem to obtain a reasonable interleaved subgradient direction. The distance to optimal solutions can be decreased step by step along this searching direction. Computation experiments demonstrate the effectiveness of the presented algorithm. Compared with regular Lagrangian relaxation based on subgradient optimization, the testing results show that the developed method can get better schedule results with less time in aspect of solution quality and computation efficiency, especially for large-sized problems.

systems engineering; interleaved subgradient method; Lagrangian relaxation; multi-stage hybrid flowshop problem; total weighted completion time

2014- 05- 12

国家自然科学基金资助项目(71001090,71001091);中国博士后科学基金资助项目(2013M531683,2014T70684);教育部人文社会科学研究青年基金项目(15YJC630148)；郑州大学优秀青年教师发展基金项目(1421326092);河南省科技攻关计划资助项目(142102310335,142102310313)

轩华(1979-)，女，河南睢县人，教授，博士，研究方向：生产计划与调度、物流优化与控制;李冰(1976-)，男，河南省开封市人，教授，博士，研究方向：物流管理等。

TB399

A

1007-3221(2015)06- 0121- 07

10.12005/orms.2015.0203