多时间窗车辆路径问题的智能水滴算法
李珍萍, 赵 菲, 刘洪伟
(北京物资学院 信息学院, 北京 101149)
多时间窗车辆路径问题的智能水滴算法
李珍萍, 赵 菲, 刘洪伟
(北京物资学院 信息学院, 北京 101149)
研究了多时间窗车辆路径问题,考虑了车容量、多个硬时间窗限制等约束条件,以动用车辆的固定成本和车辆运行成本之和最小为目标,建立了整数线性规划模型。根据智能水滴算法的基本原理,设计了求解多时间窗车辆路径问题的快速算法,利用具体实例进行了模拟计算,并与遗传算法的计算结果进行了对比分析,结果显示,利用智能水滴算法求解多时间窗车辆路径问题,能够以很高的概率得到全局最优解,是求解多时间窗车辆路径问题的有效算法。
车辆路径问题;多时间窗;数学模型;智能水滴算法
0 引言
由Dantzig和Ramser于1959年提出的车辆路径问题(vehicle routing problem,简称VRP)[1]是组合优化中一类NP难问题。该问题自提出以来,引起了运筹学和管理科学工作者的广泛关注。车辆路径问题的扩展问题也不断得到广大学者的关注。车辆路径问题的扩展情况有:需求不确定的车辆路径问题、道路信息不确定的车辆路径问题。实际物流配送中的很多问题,如连锁经营超市的商品配送问题、连锁经营餐饮门店的原料配送问题[2]、快递企业的快件收取及配送问题等,都可以归结为经典的车辆路径问题或车辆路径问题的扩展情况,因此,该问题有着广泛的应用背景。其中,带时间窗的车辆路径问题(VRPTW)是在经典车辆路径问题(VRP)的基础上加上了时间窗限制、车容量限制等约束条件,该问题属于强NP难问题。由于车辆路径问题是NP难问题,实际工作中遇到的车辆路径问题规模都比较大,因此,寻求解决车辆路径问题的快速有效算法成了解决实际问题的关键。近年来,对带时间窗的车辆路径问题(VRPTW)的研究成果主要集中在寻找带有单一时间窗问题的快速有效算法方面。
多时间窗的车辆路径问题(VRPMTW)指每个需求点都存在多个互不相交的时间窗,配送车辆必须在各个需求点对应的某一个时间窗内为其提供服务(这类时间窗称为硬时间窗,本文仅考虑具有多个硬时间窗约束的问题)。这类问题在实际中有着广泛的应用。这类问题是VRPTW问题的扩展情况,文献[3]中研究了多时间窗车辆路径问题,建立了数学模型,文献[4]提出了求解多时间窗车辆路径问题的混合蚁群算法,文献[5]设计了求解多时间窗车辆路径问题的遗传算法。
智能水滴算法(Intelligent Water Drops, IWD)是Hamed Shah-Hosseini于2007年首次提出的一种新型群智能算法。该算法通过模拟自然界水系统和其周围环境的相互作用而形成河流水道的过程进行迭代运算,最终获得优化结果。智能水滴算法最先被用于解决旅行商问题[6]。随后,Shah-Hosseini又将智能水滴算法用于解决多维背包问题、N皇后和灰度阈值问题等[7~9]。ImanKamkar等人运用智能水滴算法求解了一般车辆路径问题[10],并将智能水滴算法的运行结果与模拟退火算法[11~13]、拓扑搜索[14]、改进蚁群算法[15~17]等的运行结果进行对比,发现用智能水滴算法可以得到更好的解。为了进一步提高智能水滴算法的求解效率,部分学者还针对具体的实际问题,提出了改进的智能水滴算法[18~23]。
由于带时间窗的车辆路径问题比一般车辆路径问题考虑的因素更多,问题更复杂,文献[10]中提出的求解一般车辆路径问题的智能水滴算法并不能直接推广用于解决带时间窗的车辆路径问题。到目前为止,尚没有文献研究求解多时间窗的车辆路径问题的智能水滴算法。
本文将针对具有硬时间窗约束的多时间窗车辆路径问题的特点,建立多时间窗车辆路径问题的数学模型。进一步利用智能水滴算法的原理,设计求解多时间窗的车辆路径问题快速有效算法,以总成本最低为目标,寻找车辆的最优行驶路径。
1 多时间窗车辆路径问题的数学模型
多时间窗车辆路径问题VRPMTW可描述为:一个配送中心拥有若干辆车,为n个需求点提供配送服务,已知每个需求点的需求量、每辆车的最大装载量及任意两个需求点和配送中心之间的距离,每个需求点均有多个互不相交的服务时间窗。每辆车均从配送中心出发,为若干个需求点提供配送服务,最后再回到配送中心。假设每个需求点只能由一辆车提供配送服务,并且车辆必须在需求点的某一个给定时间窗内到达并完成配送服务;每辆车为每个需求点提供配送服务的时间(装卸货时间)已知;动用每辆车的固定成本及每辆车行驶单位距离的成本均已知;每辆车的总行驶距离(时间)不能超过给定的最长行驶距离(时间)。问应该动用几辆车以及如何安排每辆车的配送路径才能使总配送成本最低?
为了建立模型方便,定义如下符号:
K={1,2,…,m}:表示可使用的车辆集合;
D={0,1,2,…,n,n+1}:表示配送中心及客户集,其中1,2,…,n表示需求点,0和n+1表示配送中心(为了建立模型方便,本文把配送中心表示成两个点,0点表示配送车辆的出发点,n+1点表示配送车辆完成配送任务后的返回点);为了方便,本文把D中的每个元素(配送中心或需求点)简称为一个点,即第0个点和第n+1个点表示配送中心,第1,2,…,n个点表示需求点。
dij:表示从第i个点到第j个点的距离,i,j=0,1,2,…,n,n+1;k=1,2,…,m;
tij:表示车辆从第i个点到第j个点的行驶时间,i,j=0,1,2,…n,n+1;k=1,2,…,m;
sik:表示车辆k为第i个需求点提供服务(装卸货物)所需要的时间,k=1,2…,m;i=1,2,…,n;
Qk:表示车辆k的最大装载量,k=1,2,…,m;
Dk:表示车辆k的最长总行驶距离(时间),k=1,2,…,m;
qi:表示第i个需求点的需求量,i=1,2,…,n;
gk:表示动用车辆k的固定成本,k=1,2,…,m;
ck:表示车辆k行驶单位距离(时间)的成本,k=1,2,…m;
定义模型的决策变量如下:
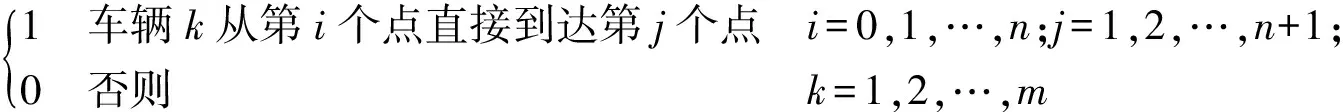


多时间窗车辆路径问题可以表示成如下整数线性规划模型
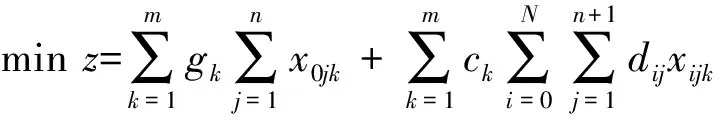
(1)
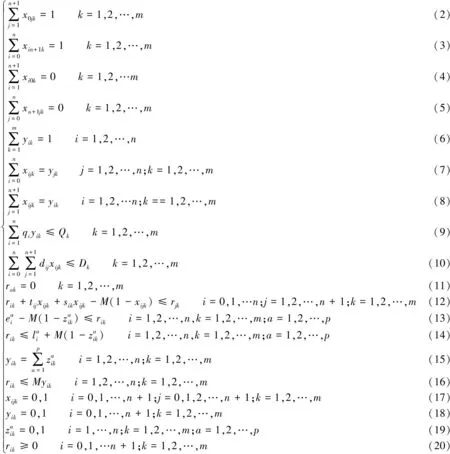
上述整数线性规划模型的含义如下:
目标函数(1)表示最小化总成本;
约束条件(2)表示每一辆车都必须从配送中心出发;
约束条件(3)表示每一辆车完成配送任务后都必须返回配送中心;
约束条件(4)表示点0为车辆的出发点,而不是车辆返回点;
约束条件(5)表示n+1点为车辆最终返回点,而不是车辆的出发点;
约束条件(6)表示恰好有一辆车为每个需求点提供服务;
约束条件(7)表示如果第k辆车到达第j个点,则必为第j个需求点提供服务;
约束条件(8)表示如果第k辆车为第i个点提供服务,则服务完必须从第i个点离开;
约束条件(9)表示任何一辆车所服务的需求点的总需求量不超过其最大装载量;
约束条件(10)表示任何一辆车的总行驶距离(时间)不超过其最大行驶距离(时间);
约束条件(11)表示每一辆车从配送中心0出发的时刻均为0;
约束条件(12)表示任何一辆车在其配送路径上相继到达两个需求点的时刻之间的关系;
约束条件(13)(14)表示如果第k辆车在第i个需求点的第a个时间窗内为其提供服务,则其到达第i个需求点的时刻必须满足第i个需求点的第a个时间窗约束;
约束条件(15)表示如果第k辆车为第i个需求点提供服务,则必须在第i个需求点的某一个时间窗内完成服务;
约束条件(16)表示如果第k辆车没有为第i个需求点提供服务,则其不会到达第i个需求点处;
约束条件(17)(18)(19)(20)表示变量取值限制。
2 智能水滴算法
2.1 智能水滴算法的基本原理
智能水滴算法是一种群智能算法,它通过模拟自然界水系统和其周围环境的相互作用而形成河道的过程进行迭代运算,最终获得优化结果。在自然界的河道中有无数流动着的水滴,这些流动的水滴与河道具有作用与反作用的关系。一方面,无数流动的水滴形成巨大的移动群体,这个巨大的水滴群体创造了河流流经的河道;另一方面河道本身也在影响着水滴的流向。如果河道中没有障碍物,那么水滴会以直线路径到达目的地,形成水滴流动的最短路径。如果有障碍物存在,水滴就会改变流动路径,形成弯曲的河道。经过科学家的研究发现,在考虑河流从源点到目的地的距离和中间障碍物存在的情况下,水滴建立起来的河道往往是最优的。
流动中水滴具有一定的速度和携带一定量的泥土,水滴能够将泥土从一个地方搬运到另一个地方。由于水滴速度越快其动能越大,因此泥土会从流速较高的地方被搬运到流速较低的地方;当流速减缓时,泥土在地球重力作用下会沉积下来。水滴流速快的地方随着时间推移会变得越来越深,同时越来越深的河道又会吸引后续更多的水滴。因此,自然界中水滴与泥土的关系满足三个规则:(1)流速快的水滴比流速慢的水滴携带更多的泥土;(2)水滴在泥土较少的路径比泥土较多的路径获得更多的速度增量;(3)水滴会以更大的概率选择泥土较少的路径前进。
在智能水滴算法中,水滴具有两个属性:水滴前进的速度和水滴携带的泥土量。这两个属性在水滴的流动过程中不断变化,目的是寻找一条最优路径。由于智能水滴有有效汇聚的能力,所以,随着迭代次数的增大,该算法找到最优解的概率也随之增大。为了简化问题,在智能水滴算法迭代过程中,假设水滴是按照离散步骤运动的。
多时间窗车辆路径问题可以用图G=(V,E)表示其中,V={0,1,2,…,n}表示节点集合(包括配送中心0和需求点1,2,…,n),E表示节点之间的边集合。一个水滴从配送中心0出发,沿着不同的路径,遍历各个需求点,最后回到配送中心,形成水滴的完整流动路径(路径中水滴可以多次经过配送中心0,但每个需求点只能经过一次),每一个水滴的完整流动路径恰好对应了VRPMTW的一个解。
如某个水滴的完整流动路径为0→4→2→0→3→6→7→0→8→5→1→0,则表示需要用3辆车完成配送任务,3辆车的配送路径分别为:0→4→2→0,0→3→6→7→0,0→8→5→1→0。
如果所有的水滴都形成了各自的完整流动路径,则一次迭代结束。每次迭代结束后,在各个水滴的完整流动路径中找出最优的路径TIB,利用这条最优路径更新各个节点之间的泥土量及全局最优路径TTB;然后进入下一次迭代。不断重复这种迭代过程,直到达到最大迭代次数Itermax或者得到期望的最优路径TTB。
2.2 智能水滴算法的计算步骤
第1步 输入初始静态变量:
配送中心及需求点集合,0表示配送中心,1,2, 3,…,n表示需求点;
需求点个数n;
配送中心及各个需求点之间的距离矩阵D;
车辆的单位行驶成本h;
动用每辆车的固定成本g;
车辆的行驶速度v;
每辆车的最大装载量Qmax;
车辆在配送中心及各个需求点之间行驶的时间矩阵T;
最大迭代次数Iter;
水滴个数M;
速度更新参数:av,bv,cv;
泥土量更新参数:as,bs,cs;
局部泥土更新权系数α;
全局泥土更新权系数β;
任意两点间的初始泥土量Initsoil;
初始泥土量矩阵W=(wij)(n+1)×(n+1),其中w(i,j)=Initsoil;
每个水滴的初始速度Initvel。
第2步 输入初始动态变量
每个水滴已访问过的节点集合Visitnode,初始状态为空集;
每个水滴未访问过的节点集合Novisitnode,初始状态为Novisitnode= {0,1,2,…,n};
每个水滴从配送中心出发时携带的初始泥土量Soil=0;
每个水滴从配送中心出发时的初始速度Vel=InitVel;
每个水滴从配送中心出发时的初始装载量Q(0)=0;
每个水滴从配送中心出发的时刻r(0)=0。
第3步 按照下列步骤(1)--(6)求出每个水滴对应的访问路径(每个水滴的访问路径对应VRPMTW的一个可行解)
(1) 根据时间窗限制,从符合约束条件的需求点中随机选择一个需求点作为水滴访问的第一个节点,记录水滴到达该节点的时刻。
(2)更新水滴已经访问过的节点集合Visitnode及未访问节点集合Novisitnode,并记录水滴已访问节点的访问顺序。
(3) 根据每个水滴的未访问节点对应的时间窗及未访问节点的需求量,确定水滴从当前节点出发下一个可访问的节点集合FV(如果水滴从当前节点去某一个未访问节点,到达未访问节点时的容量约束和时间窗限制均满足,则将该未访问节点加入下一个可访问节点集合FV);如果所有的未访问节点都不满足容量约束和时间窗限制,则水滴返回配送中心,将该水滴对应的动态变量恢复初始值(表示一辆车的配送路径已经形成);如果未访问节点集合为空集,则水滴返回配送中心,该水滴的完整访问路径已经形成,水滴的完整访问路径对应VRPMTW问题的一个可行解TIWD。
(4)计算集合FV中每一个可访问节点对应的访问概率。
水滴从当前节点i出发,到FV中每一个可访问节点j的概率可以按照以下的公式计算:
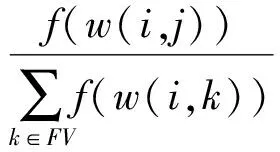
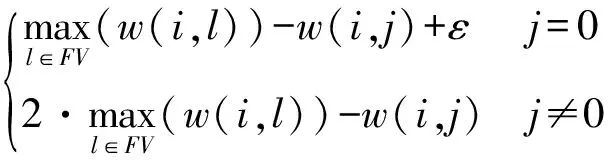
此处,当j=0时的计算公式与其它情况下不同,主要目的是尽可能减少不满载车辆直接返回配送中心的概率。
(5)根据集合FV中每个节点对应的概率,用赌轮法选择下一个访问点。如果水滴选择的下一个访问节点为j,则将节点j加入到已访问节点集合中,并修改当前水滴对应的已访问节点集合、访问顺序和未访问节点集合。
(6)更新水滴对应的动态变量
更新水滴的流速:
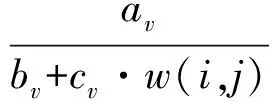
计算水滴到达节点j的时间r(j)及装载量Q(j):
r(j)=r(i)+s(i)+tij
Q(j)=Q(i)+qj
计算水滴从节点i流到节点j时携带泥土的增量
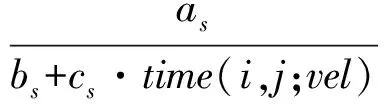

更新水滴流过的路径(i,j)上的泥土量w(i,j):
w(i,j)=w(i,j)-α·Δsoil(i,j)
更新水滴携带的泥土量
soilIWD=soilIWD+Δsoil(i,j)
水滴携带的泥土增量取决于水滴流动的速度,在VRPMTW中,水滴携带的泥土增量与水滴流过该段路径所用的时间有关。流速较快的水滴会比流速较慢的水滴携带更多的泥土量。
第4步 在第三步求出的所有水滴的完整访问路径TIWD中,寻找最优解TIB
每个水滴的完整访问路径对应VRPMTW问题的一个可行解,计算其目标函数值(总配送成本),通过比较确定出目标函数值最小的一个可行解TIWD,作为本次迭代的最优解TIB。
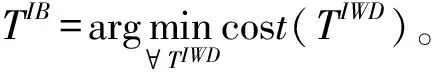
第5步 利用本次迭代得到的最优解TIB,更新其对应的最优路径上的泥土量,并把更新以后的泥土量矩阵作为下一次迭代的初始泥土量矩阵。
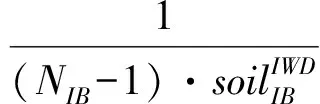
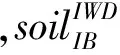
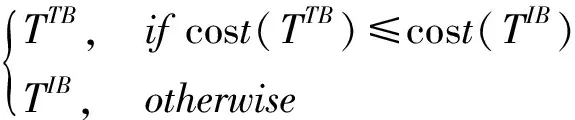
第7步 更新迭代计数
Itercount=Itercount+1
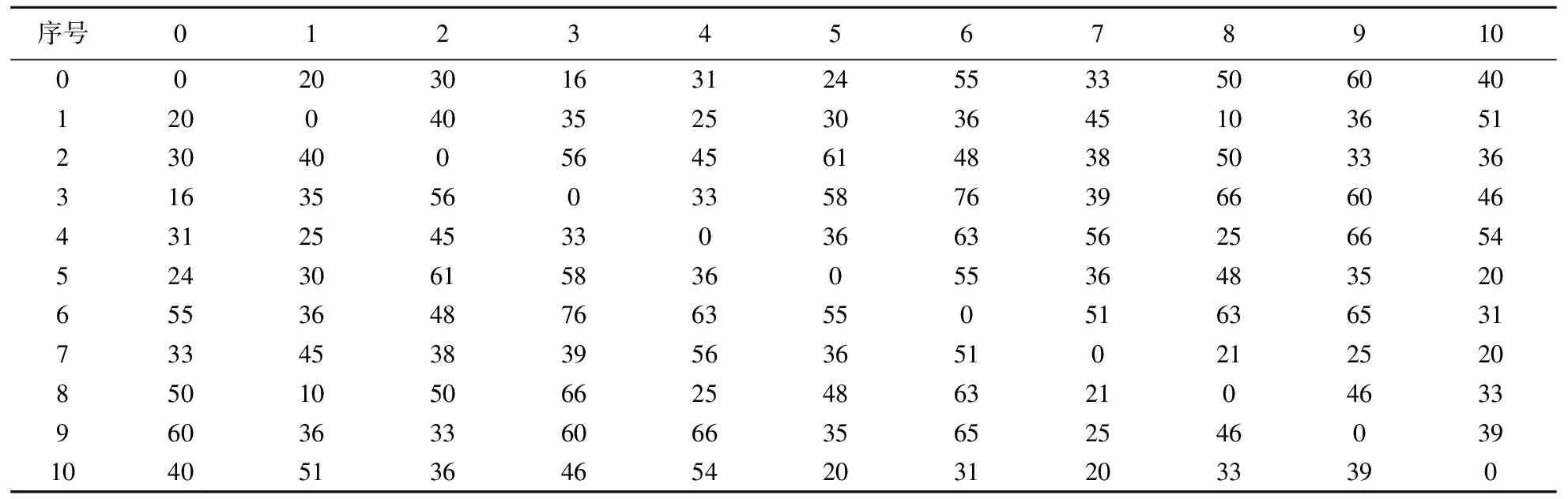
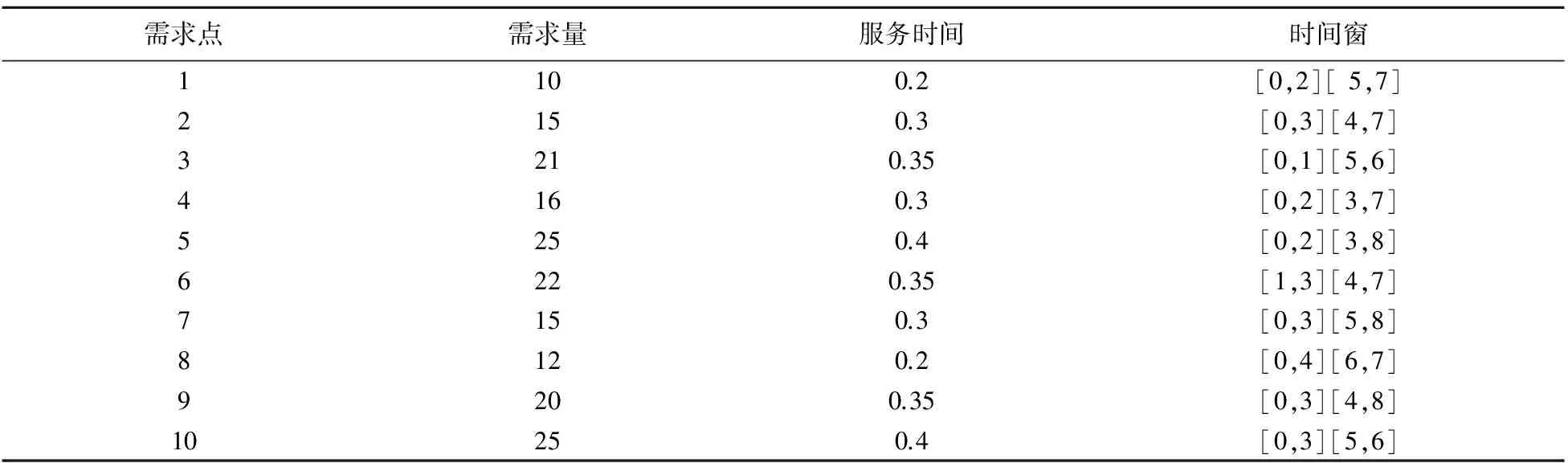
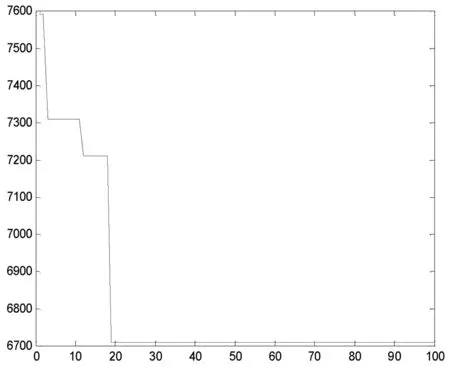
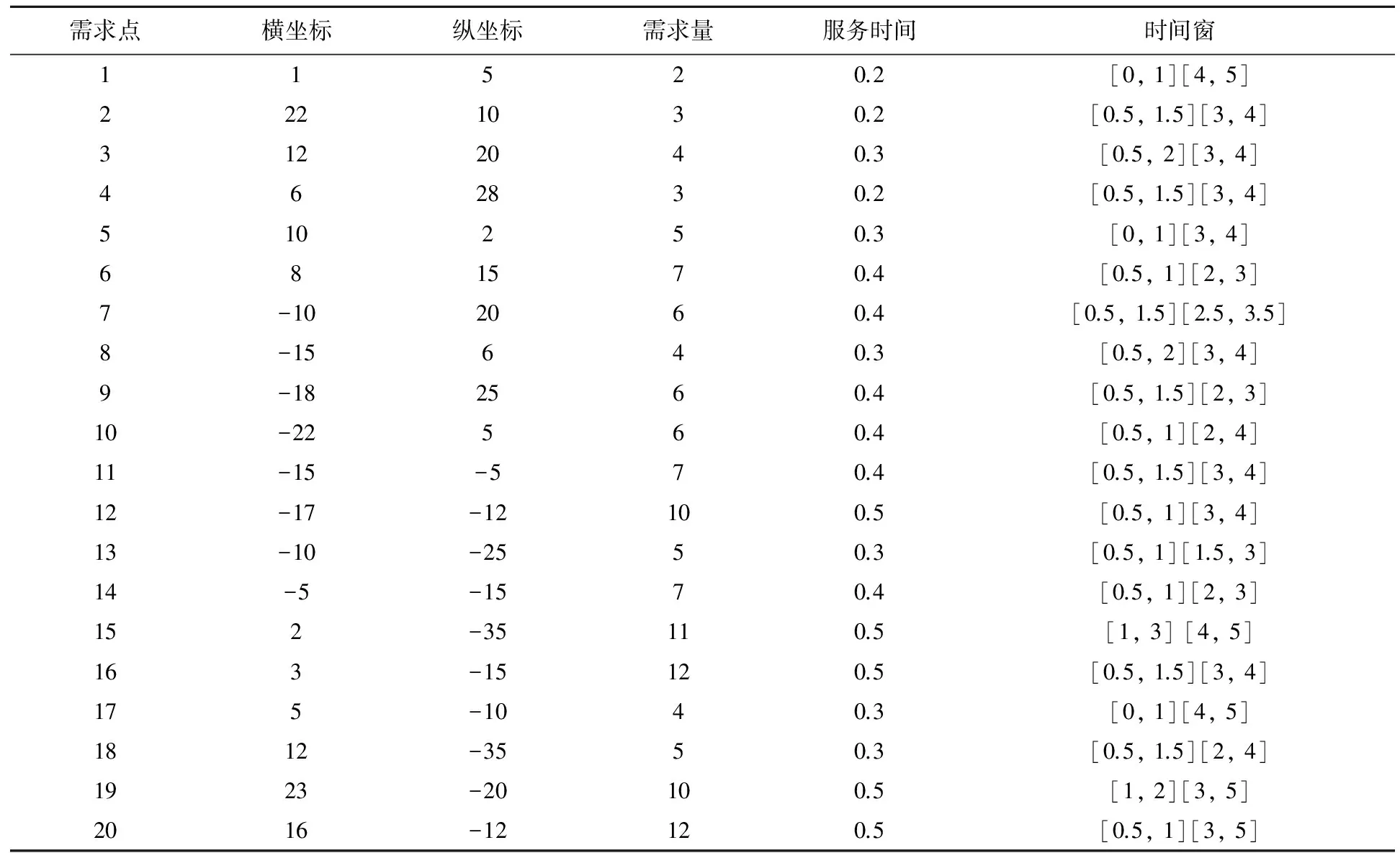
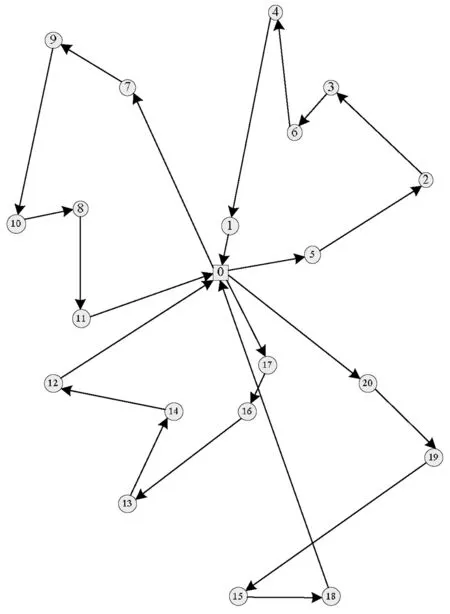
如果Itercount 如果Itercount=Itermax,则将最后得到的解TTB作为VRPMTW问题的最优解输出,计算结束。 首先我们选取文献[5]中的实例,利用智能水滴算法进行计算,并与文献[5]中的计算结果进行对比。 表1 配送中心与各需求点之间的距离(单位:公里) 表2 各需求点的需求量(单位:吨),服务时间(单位:小时)和2个时间窗 图1 智能水滴算法的收敛过程,横坐标表示迭代次数,纵坐标表示目标函数最优值 利用Lingo软件编写程序,直接求解整数规划模型,可以得到本例的精确最优解,共需要动用3辆配送车,配送路径分别为:0→2→9→7→8→4→0,0→1→6→10→5→0,0→3→0。总配送距离为328公里,总配送成本为6710元。 由于直接求解整数规划模型时间太长,本文同时利用智能水滴算法求解,采用以下运行参数:水滴数NIWD=100;水滴流速更新参数av=1,bv=0.1,cv=1;水滴携带泥土量更新参数as=1,bs=0.1,cs=1;局部泥土量更新参数α=1;全局泥土量更新参数β=1;需求点之间边上的初始泥土量InitSoil=2000;水滴从配送中心出发的初始速度InitVel=100;最大迭代次数Itermax=100。利用这组参数一共进行了100次运算,其中96次得到了问题的精确最优解。最快的一次仅迭代3次就得到了全局最优解,最慢的一次迭代了35次得到全局最优解,平均迭代次数为14次。图1描述了其中一次运算的收敛过程。 利用文献[5]中遗传算法求解本例, 选取种群规模为100,最大迭代次数为100,利用这组参数运行算法100次,仅有30次得到问题精确最优解,在得到精确最优解的运算中,最快的一次迭代次数为16次,最慢的一次迭代次数为86次,平均迭代次数为54次。 针对例1,分别利用遗传算法(GA)和智能水滴算法(IDW)计算100次,统计100次计算中找到最优解的次数,得到的目标函数平均值,得到的最差解的目标函数值,收敛到最优解需要的最少迭代次数和最多迭代次数,以及平均迭代次数等,得到的统计结果见表3。 表3 分别利用遗传算法和智能水滴算法运行100次的结果统计表 通过以上分析及表3中统计结果的比较可以看出,智能水滴算法无论在得到最优解的概率还是收敛到最优解的迭代次数方面都明显优于遗传算法。 文献[4]中对于同样规模的问题,利用元胞蚁群算法计算,100次运算中平均仅有15次能得到最优解。可见元胞蚁群算法在找到最优解的概率方面更是远远不如智能水滴算法。 例2 某配送中心拥有若干辆型号相同配送车辆,每天为配送范围内的20个需求点提供配送服务。用序号0表示配送中心,序号1到20表示需求点,假设配送中心的位置坐标为(0,0), 各个需求点的位置坐标、需求量qj、配送车辆为各个需求点提供服务的时间ssj,各个需求点要求服务的2个时间窗等如表4所示。已知每辆配送车辆的最大装载量为Q=40吨, 所有的配送车辆0时刻从配送中心出发,完成配送任务后必须在8小时之内返回配送中心。假设配送车辆的行驶时间和距离成正比,平均行驶速度为30千米/小时,需求点i到需求点j的距离等于两点间的直线距离,动用一辆配送车辆的固定成本为100元,配送车辆行驶每公里的成本为5元。求使总成本最低的配送路径。 表4 各需求点的位置坐标(公里)、需求量(吨)、服务时间(小时)、时间窗(小时) 利用智能水滴算法求解,采用以下运行参数:水滴数N=200;水滴流速更新参数av=1000,bv=0.1,cv=1;水滴携带泥土量更新参数as=1000,bs=0.1,cs=1;局部泥土量更新参数α=0.9;全局泥土量更新参数β=0.9;需求点之间边上的初始泥土量InitSoil=2000;水滴从配送中心出发的初始速度InitVel=100;最大迭代次数Itermax=800。 经过计算,得到VRPMTW问题的最优解,如图2所示。共需动用4辆车完成配送任务,最小总费用为2168.9元,其中第一辆车的配送路径为0→5→2→3→6→4→1→0,实际最大装载量为24吨,配送路径长度为86.966公里;第二辆车的配送路径为0→7→9→10→8→11→0,实际最大装载量为29吨,配送路径长度为86.073公里;第三辆车的配送路径为0→17→16→13→14→12→0,实际最大装载量为38吨,配送路径长度为77.325公里;第四辆车的配送路径为0→20→19→15→18→0,实际最大装载量为38吨,配送路径长度为103.44公里。 图2 最优配送路径示意图 从图2中可以看出,为了满足各个需求点的时间窗限制,有些配送车辆的配送路径未必是最短的。如第一辆配送车辆的配送路径为:0→5→2→3→6→4→1→0,实际上,如果第一辆车按照0→5→2→6→3→4→1→0或者0→5→2→3→4→6→1→0的顺序配送,则总行驶距离均有所减少,但按照这两种配送顺序到达需求点4的时刻均不在需求点4的两个时间窗内,因此,这些行程较短的配送路径并不可行。另外,在第四辆车的配送路径0→20→19→15→18→0中,如果把需求点15和需求点18的顺序交换,则路径的长度将减少,但交换顺序后的路径无法满足需求点15的时间窗限制。通过对其他例子的计算结果分析也可以发现类似的情况,这说明,智能水滴算法在求解的过程中已经综合考虑了各种约束条件,得到的解在实际中具有很好的可操作性。 本文还采用不同的参数进行了模拟计算,从大量的计算结果中可以发现,智能水滴算法能够有效跳出局部最优解,快速地找到问题的近似最优解,而且有较高的概率得到全局最优解。如果增加水滴个数或迭代次数,可以提高找到全局最优解的概率。 多时间窗车辆路径(VRPMTW)问题在实际中有着非常广泛的应用,由于该问题是典型的NP难题,精确求解非常困难,因此设计求解多时间窗车辆路径问题的快速有效算法是解决实际物流配送问题的关键。智能水滴算法是一种新型的群体智能算法,本文利用智能水滴算法基本原理设计了求解多时间窗车辆路径问题的快速有效算法,通过仿真实验证明了智能水滴算法的良好效果,智能水滴算法能够以较大概率找到全局最优解,是求解多时间窗的车辆路径问题的一个很好的方法。 由于智能水滴算法能够有效地跳出局部最优解,在解决诸多组合优化问题中均显示了良好的效果,因此还可以利用智能水滴算法的基本原理设计求解其它组合优化问题的快速有效算法。 本文仅考虑了具有多个硬时间窗约束的车辆路径问题,即必须在客户的某个时间窗内为其提供服务,既不能早到,也不能晚离开。对于具有多个软时间窗的车辆路径问题,也可以利用智能水滴算法的原理设计相应的快速求解算法。 [1] Dantzig G, Ramser J. The truck dispatching problem[J]. Management Science, 1959, 10 (6): 80-91. [2] Shi Z, Fu Z. Research on two-phase chain store distribution vehicle routing problem with soft time windows[J]. Application Research of Computers, 2012, 29 (9): 94-99. [3] Ma H, Zuo C, Yand S. Modeling and solving for vehicle routing problem with multiple time windows[J]. Journal of System Engineering, 2009,24, (05): 607- 613. [4] Peng B, Zhou Y. Hybrid ant colony algorithm for vehicle routing problem with multiple time windows[J]. Computer Engineering and Applications, 2010, 46 (31): 28-31. [5] Huang Q, Li Z. Mathematical model and algorithm for vehicle routing problem with multiple time windows[J]. Logistics Technology, 2012, 31(7): 194-196. [6] Hamed Shah-Hosseini. (2007). Problem Solving by Intelligent Water Drops[A]. Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 2007. 3226-3231. [7] Hamed Shah-Hosseini. The intelligent water drops algorithm: a nature-inspired swarm-based optimization algorithm[J]. Bio-Inspired Computation, 2009, Vol. 1, Nos. 1/2. 71-79. [8] Hamed Shah-Hosseini. Optimization with the nature-inspired intelligent water drops[A]. In W. P. Dos Santos(Eds), Evolutionary computation, Austria: I-Tech, Vienna, 2009. 297-320. [9] Hamed Shah-Hosseini. Intelligent water drops algorithm for automatic multilevel thresholding of gray-level images using a modified Otsu’s criterion[J]. International Journal of Modeling, Identification and Control(IJMIC), 2012, 15(4): 241-249. [10] Kamkar, Akbarzaden, Yaghoobi. Intelligent water drops a new optimization algorithm for solving the Vehicle Routing Problem[A]. IEEE International Conference on Systems Man and Cybernetics, 2010. 4142- 4146 [11] Tavakkoli-Moghaddam R, Safaei N, Ghlipour Y. A hybrid simulated annealing for capacitated vehicle routing problems with the independent route length[J]. Applied Mathematics and Computation, 2006, 176: 445- 454 [12] Prins C. A simple and effective evolutionary algorithm for the vehicle routing problem[J]. Computers & Operations Research, 2004, 31: 1985-2002. [13] Geonwook Jeon, Herman R. Leep, Jae Young Shim. A vehicle routing problem solved by a hybrid genentic algorithm[J]. Journal of Computers and Industrial Engineering, 2007, 53(4): 680- 692. [14] Renaud J, Laporte G, Boctor F F. A tabu search heuristic for the multi-depot vehicle routing problem[J]. Computers & Operations Research, 1996, 23 (3): 229-235. [15] Doerner K F, Hartl R F, Kiechle G, Lucka M, Reimann M. Parallel ant systems for the capacitated vehicle routing problem[A]. Evolutionary Computation in Combinatorial Optimization: 4th European Conference, EvoCOP 2004, LNCS 3004, 72- 83. [16] Reimann M, Stummer M, Doemer K. (2002).A savings based ant system for the vehicle routing problem. Langdon,W.B. et al.(Eds), GECCO 2002: Proceedings of the Genetic and Evolutionary Computation Conference, Morgan Kaufmann, San Francisco. [17] Peng W, Tong R F, Tang M, Dong J X. (2005). Ant colony search algorithms for optimal packing problem. ICNC 2005, LNCS 3611, 1229-1238. [18] Msallam M M, Hamdan M. Improved intelligent water drops algorithm using adaptive schema[J]. Bio-Inspired Computation, 2011, 3(2): 103-111. [19] Hamed Shah-Hosseini. (2012). An approach to continuous optimization by the intelligent water drops algorithm. The 4th International Conference of Cognitive Science, 224-229. [20] Niu S H, Ong S K, Nee A Y C. An improved intelligent water drops algorithm for achieving optimal job-shop scheduling solutions[J]. International Journal of Production Research, 2012, 50: 15, 4192- 4205 [21] Hamed Shah-Hosseini. Intelligent water drops algorithm: a new optimization method for solving the multiple knapsack problem[J]. International Journal of Intelligent Computing and Cybernetics, 2008, 1(2): 193-212. [22] Duan H, Liu S, Lei X. (2008). Air robot path planning based on intelligent water drops optimization. IEEE International Joint Conference on Neural Networks(IJCNN2008), 1(8): 1397-1401. [23] Duan H, Liu S, Wu J. Novel intelligent water drops optimization approach to single UCAV smooth path planning[J]. Aerospace Science and Technology, 2009, 13: 442- 449. Intelligent Water Drops Algorithm for Vehicle Routing Problem with Multiple Time Windows LI Zhen-ping, ZHAO Fei, LIU Hong-wei (SchoolofInformation,BeijingWuziUniversity,Beijing101149,China) The vehicle routing problem with multiple time windows is investigated in this paper. The constraints of vehicle’s capacity and the multiple hard time windows are considered. An integer linear programming model of VRPMTW is proposed, and the objective function is to minimize the total costs including the fixed costs of vehicles and the transportation costs of vehicles. Based on the principles of the intelligent water drops, an Intelligent Water Drops(IDW)algorithm for solving the VRPMTW is designed. We further do simulation on an example, and compare the results obtained by IDW algorithm and GA(genetic algorithm)algorithm. The results show that we can find the global optimal solution of VRPMTW with higher probability using Intelligent Water Drops algorithm than Genetic Algorithm. IDW algorithm is an efficient algorithm for solving VRPMTW. Key words:vehicle routing problem; multiple time windows; mathematical model; intelligent water drops algorithm 2014- 05-10 国家自然科学资助项目(11131009,71540028);北京市属高等学校长城学者培养计划项目(CIT&TCD20130327);北京市科委项目《用于电子商务物流的搬运机器人与多机器人现场控制系统研制及应用验证》;北京物资学院重大科研项目《基于可移动货架的订单拣选优化问题研究》。 李珍萍(1966-),女,博士,教授,研究方向:智能算法,复杂网络;赵菲(1991-),女,硕士研究生,研究方向:物流工程;刘洪伟(1977-),男,博士,讲师,研究方向:最优化理论。 O226 A 1007-3221(2015)06- 0001-10 10.12005/orms.2015.1893 仿真实验与结果分析
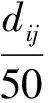

4 结论

