总量控制和交易环境下考虑随机需求的企业决策分析
熊 轶, 陈智民, 霍佳震, 潘燕春, 周 明
(1.同济大学 经济与管理学院,上海 200092; 2.深圳大学 管理学院,广东 深圳 518060)
总量控制和交易环境下考虑随机需求的企业决策分析
熊 轶1,2, 陈智民2, 霍佳震1, 潘燕春2, 周 明2
(1.同济大学 经济与管理学院,上海 200092; 2.深圳大学 管理学院,广东 深圳 518060)
总量控制和交易(Cap-and-Trade, C&T)给排放企业运营决策带来了新的挑战。本文提出一个非线性优化模型分析C&T环境下的企业最优产量,并在绿色改进和碳权交易之间有效权衡。模型不仅考虑了随机需求和碳价波动,还考虑了绿色改进的边际递减效果和实施绿色生产的风险。理论分析证明了最优解的存在性,并给出了排放企业的最优决策及C&T环境下企业新的生产条件。解析分析表明:与非C&T环境相比,新的最优产量更低,实际排放下降;碳配额虽然影响企业利润和碳权交易量,但不影响最优产量和最优改进投资;碳价和绿色改进系数越大,越有利于促进企业实施绿色改进减少排放;企业利润随绿色改进系数和碳配额的增加而上升,随单位产品碳排放的增加而下降。数值分析验证了理论模型及其分析结果;蒙特卡洛模拟揭示利润波动受需求风险、绿色改进风险和碳价波动的影响,但需求风险对利润波动的影响更为显著。
总量控制和交易;随机需求;绿色改进;非线性优化;决策分析
0 引言
全球变暖等环境问题对人类生活造成了严重影响[1]。越来越多的科学家认为当前的气候改变和其它诸多环境问题是由人类自身活动引起,尤其是能源消耗产生的温室气体排放所致[1,2]。为减少温室气体排放(通常以二氧化碳排放当量CO2E计算),总量控制与交易(Cap-and-trade, C&T)被世界各国广泛采用[3]。C&T环境下,政府首先根据历史排放和减排目标,为排放企业分配一定数量的碳配额,如果企业实际排放低于配额,则剩余的排放权将成为企业的一种特殊资源,可在碳市场出售获取额外收益;企业也可通过碳市场购买排放权以弥补实际超排量[4]。我国能源消耗和碳排放均居世界第一[5],面对越来越大的减排压力,政府一方面积极推进碳市场建设,如深圳排放权交易试点[6];另一方面,也不断出台更为严苛的强制性减排措施和法规(如《节约能源法》)。因此,作为碳排放主体的广大制造型企业,在C&T环境下面临更加严峻的挑战。为规避政府的严惩措施,企业可改进生产过程减少排放,但实施绿色改进存在技术、组织、财务等诸多风险,可能导致投资高、见效慢、周期长等问题[7];而且绿色改进投资本身还具有边际效果递减特征,即随着绿色改进的进行,减少相同排放的成本将越来越高[8,9]。有关碳市场的研究则表明,碳价格、碳收益等的变化都不服从均值回归过程,碳市场面临着比股票市场更大的风险[10]。此外,C&T环境还会对生产计划造成重要影响,单纯由市场需求确定的最优产量可能不再最优:高产量导致的高排放可能产生高额的超排(惩罚)成本;低产量排放小则可能使企业获得额外排放权进而在碳市场交易带来减排收益。因此,如何确定新的最优产量,以及如何在绿色改进和碳权交易之间有效权衡,是C&T环境下企业亟待解决的重要决策问题。
目前相关研究大多集中在初始碳配额的分配和碳交易机制的设计等宏观层面[11~14]。鉴于C&T环境下的碳排放约束,企业微观经营决策问题越来越受到学者们的关注。Hua等[15]提出具有排放约束的经济订货批量(EOQ)模型,在确定性需求条件下,通过解析求解的方法研究了碳排放配额、碳权交易价格、碳排放与总成本的关系;Bouchery等[16]将可持续发展目标引入经典EOQ模型,在确定性需求和单周期条件下,构建了一个零售商的单级库存模型,以及一个零售商和一个仓库的二级库存模型,并分析了模型的有关数量特征;Chen等[17]研究了具有碳排放约束的EOQ模型,通过解析方法得到了新的最优订货量,并分析了碳排放和库存成本平衡的条件;国内的何大义和马洪云[18]基于存储论的分析框架,建立了企业在碳排放约束下的生产与存储优化决策模型,通过解析求解得到了企业的最优产量、碳排放权交易和净化处理决策,并用数值实验方法分析了产品市场需求波动、碳交易价格变化和产品价格变化对企业最优决策的影响;Rong和Lahdelma[19]针对某能源生产企业,鉴于碳排放权可在多期交易,提出一个多周期随机优化模型,确定热能和电能的产量计划,并使用随机仿真技术得到最优的产量组合;Catalao等[20]针对电量生产的短期计划问题,考虑能源消耗成本和碳排放约束,构建了多目标混合整数与非线性规划模型,采用ε-constraining方法求解,得到了能源成本与碳排放量的非劣解集(Pareto-optimal solution set);Absi等[21]则研究了具有碳排放约束的最优生产批量(Lot-sizing)问题,构建数学规划模型,在小规模确定性条件下得到了解析解。
除库存问题之外,一些学者还研究了存在减排目标的企业资源分配问题。Kockar等[22]将碳排放交易成本和碳排放配额引入运作成本函数和约束条件中,构建了单周期确定性数学规划模型,用于优化电厂在购买碳排放权与承担超排罚款之间的权衡决策;魏一鸣等[23]采用多智能体模型模拟碳配额机制与相关政策变量对电价和电源结构的影响,进而对基于排放和基于产出的配额方式进行比较;Wang等[9]提出一个随机规划模型分析三种可能的绿色改进途径,即使用减排设备、引进减排技术、改变能源结构,并构建拉格朗日函数求得了模型的最优解;Chang等[24]将环境因素纳入某固体废弃物管理系统的运作优化过程,分别考虑总成本最小、净收益最大、环境污染最小等不同优化目标,构建了混合整数规划模型和线性规划模型,采用LINGO软件求解的结果表明,强制性碳减排给企业资源配置带来了重大影响,考虑环境规制成本后,使用新的物料回收技术和设备将比传统的废弃物填埋决策更有优势。国内学者郑燕等[25]针对受碳减排约束的火电生产企业,基于维纳过程-伊滕引理,构建了随机动态规划模型,通过解析求解和简单的数值实验,分析了购买碳排放权和转换燃料两种资源配置策略之间的内在联系和成本、收益特征;杜少甫[26]和桂云苗[27]等学者研究了排放依赖型企业的资源分配问题,假定生产商可通过政府配额、市场交易和净化处理三种渠道获得排放许可,考虑产品市场需求的不确定性,建立了数学规划模型,在单周期和线性条件下得到资源的最优分配策略,并使用数值实验进行参数的敏感性分析,从而确定最优决策的临界条件。
本文重点研究C&T环境下,同时考虑需求不确定、碳价波动和绿色改进风险的企业运作决策问题,通过模型分析为政府当前绿色减排政策(如碳市场交易成本和碳配额等)的制定提供依据。相比现有研究,我们的贡献在于:(1)提出了一个多元非线性优化模型刻画和解决C&T环境下的企业决策问题,该模型不仅考虑了碳排放约束、需求和碳价波动,还考虑了绿色改进的边际递减效果及其风险;(2)证明了最优解的存在性,并分析了经济绩效和环境绩效与各系统参数之间的关系;(3)数值分析进一步验证了理论模型,蒙特卡洛模拟则给出了需求风险、碳市场风险(主要为碳价)和绿色改进风险与最优产量和企业利润的量化关系。本文的后续内容组织如下:第二部分在提出基本假设的基础上构建决策模型;第三部分对模型进行理论分析并提出有关命题;第四部分进行数值实验和蒙特卡洛模拟分析;第五部分给出研究结论和探讨。
1 基本假设与模型构建
本文考虑C&T环境下,制造商(排放企业)在一定时期内(如一年)的生产决策问题。假设市场需求存在随机波动;政府根据企业历史排放和减排目标确定其碳排放配额,如果企业实际排放超过配额,政府将实施高额惩罚;作为理性决策者,企业可通过绿色改进措施来减少排放,或者通过碳权交易来规避政府惩罚。假设绿色改进的减排效果当期可以实现(如使用清洁原料等),但其投资具有边际效果递减特征;而在碳市场中,碳权交易可以实现。企业面临的决策问题可描述如下:在C&T环境下,考虑随机需求、碳价波动和绿色改进风险,如何确定最优产量,如何在绿色改进与碳权交易之间有效权衡,以最大化企业利润?为更好构建问题模型,定义如下变量和参数:
x1为生产量。因为固定生产成本对模型结构没有影响(求导后不会出现在最优解表达式中),而且固定生产成本一般需要折旧,因此在本模型中未予考虑。假设产品单位生产成本(变动成本)为v,则总生产成本可表示为C1=vx1;
x2为绿色改进投资,是企业的成本支出,记C2=x2;
x3为碳权交易量,正值为买入排放权,负值为卖出;
D为产品需求,考虑为随机变量,其概率密度函数为f(D),概率分布函数为F(D),均值为μ(D),标准差为σ(D),假设F(D)连续可微;
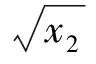
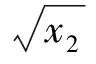
p1为产品售价,因此销售收入为R=p1·min{D,x1};
p2为碳价(碳排放权交易价格,含碳市场交易成本)。引入碳价波动风险(随机变量)α,其概率密度函数为u(α),概率分布函数为U(α),均值为μα=0,标准差为σα,假设U(α)连续可微,α与ε、D相互独立,则碳交易总额可表示为C3=(1+α)p2x3,正值为购碳成本,负值为售碳收益;
h为单位产品库存成本,因此库存总成本可表示为C4=h·max(x1-D,0);
l为单位产品缺货成本,因此缺货总成本可表示为C5=l·max(D-x1,0);
Q为政府分配给企业的碳配额。
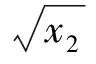
(1)
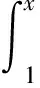
(2)
因此,该优化问题可建模如下:
决策变量:x1,x2;目标函数:最大化期望利润
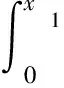
约束条件:x1≥0,x2≥0
这是一个多元非线性优化问题,下面将对模型的最优解及其特征展开分析。
2 模型分析
由式(2)可得出以下命题:
命题1 企业期望利润函数是严格上凸的,其最优产量、最优改进投入分别为:
(3)
(4)
证明E(π)分别对x1和x2求一阶和二阶偏导得:
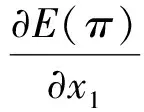
(5)
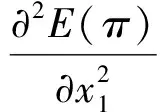
(6)
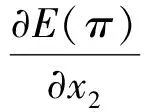
(7)
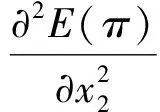
(8)
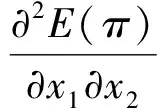
(9)
命题2 在C&T条件下,企业生产的基本条件是p1+l>v+p2b。
从命题2可以看出,如果p1+l≤v+p2b,企业的最优决策是放弃生产。与传统生产条件相比,C&T环境增加了一项碳排放成本(p2b),即企业生产时需要考虑排放成本的影响。
命题3 政府碳配额Q会影响企业的期望利润和碳权交易量,但不影响最优产量和最优改进投入。
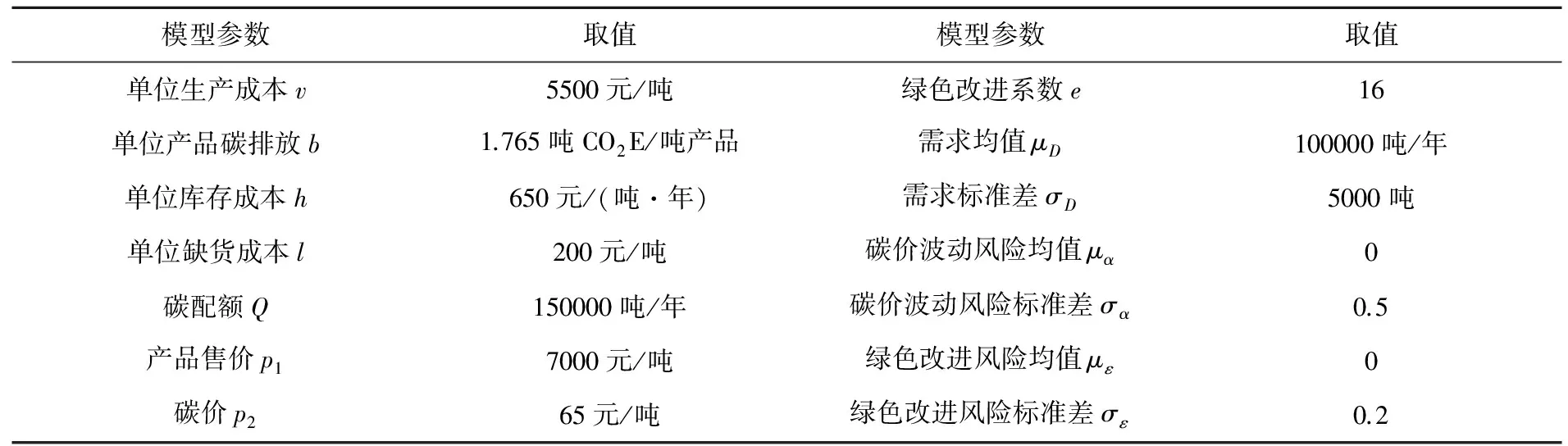
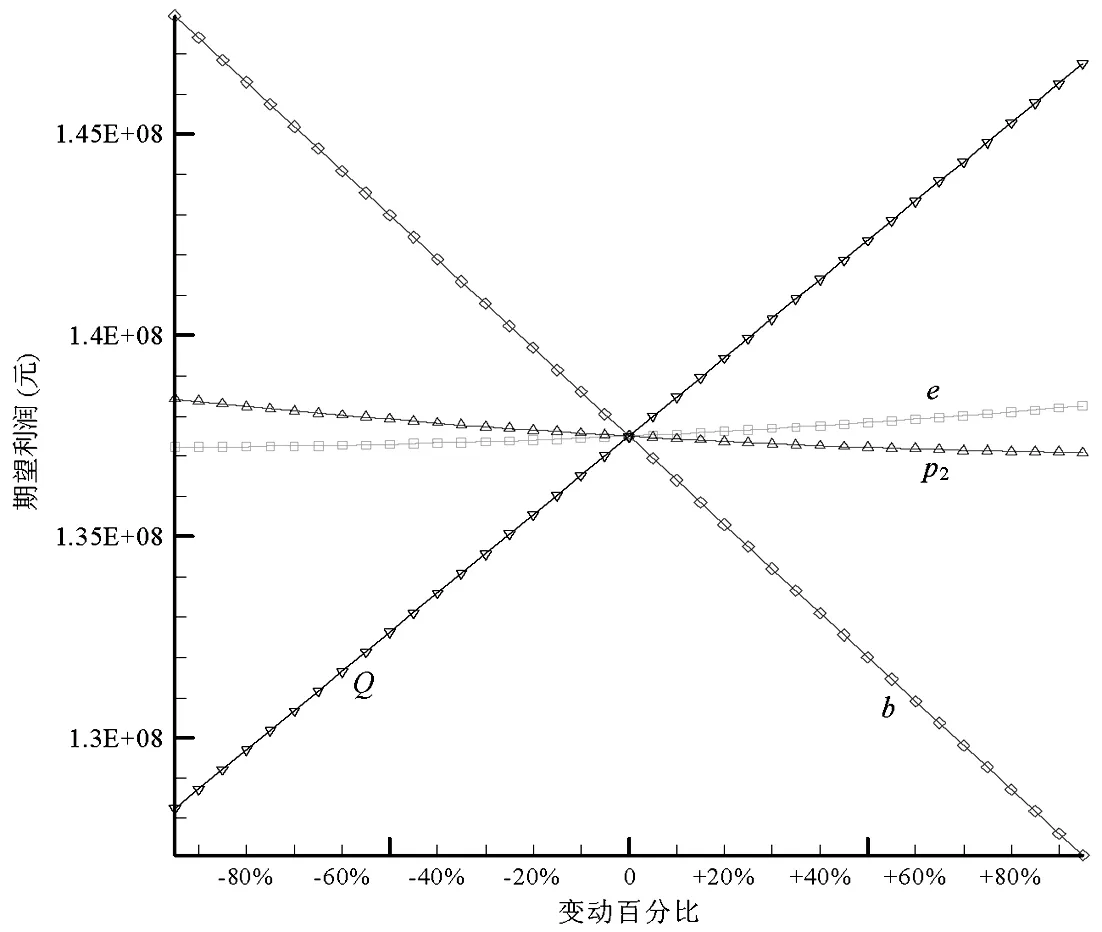
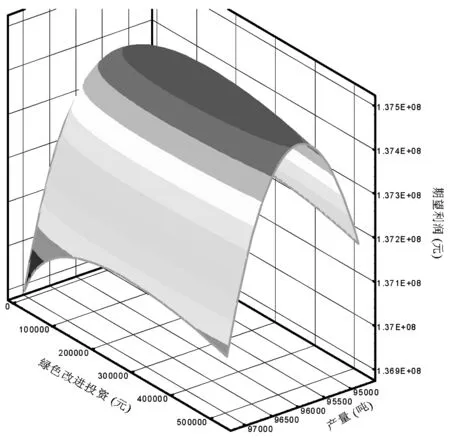
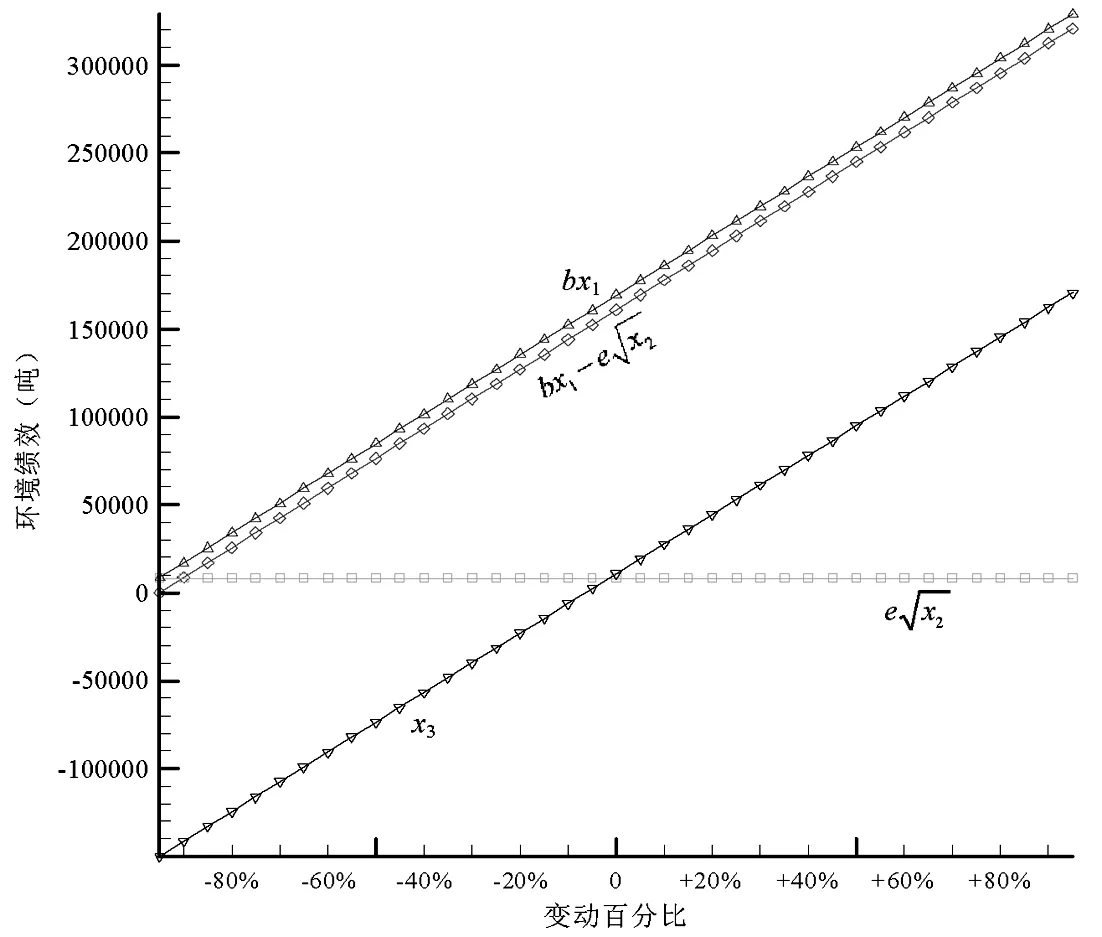
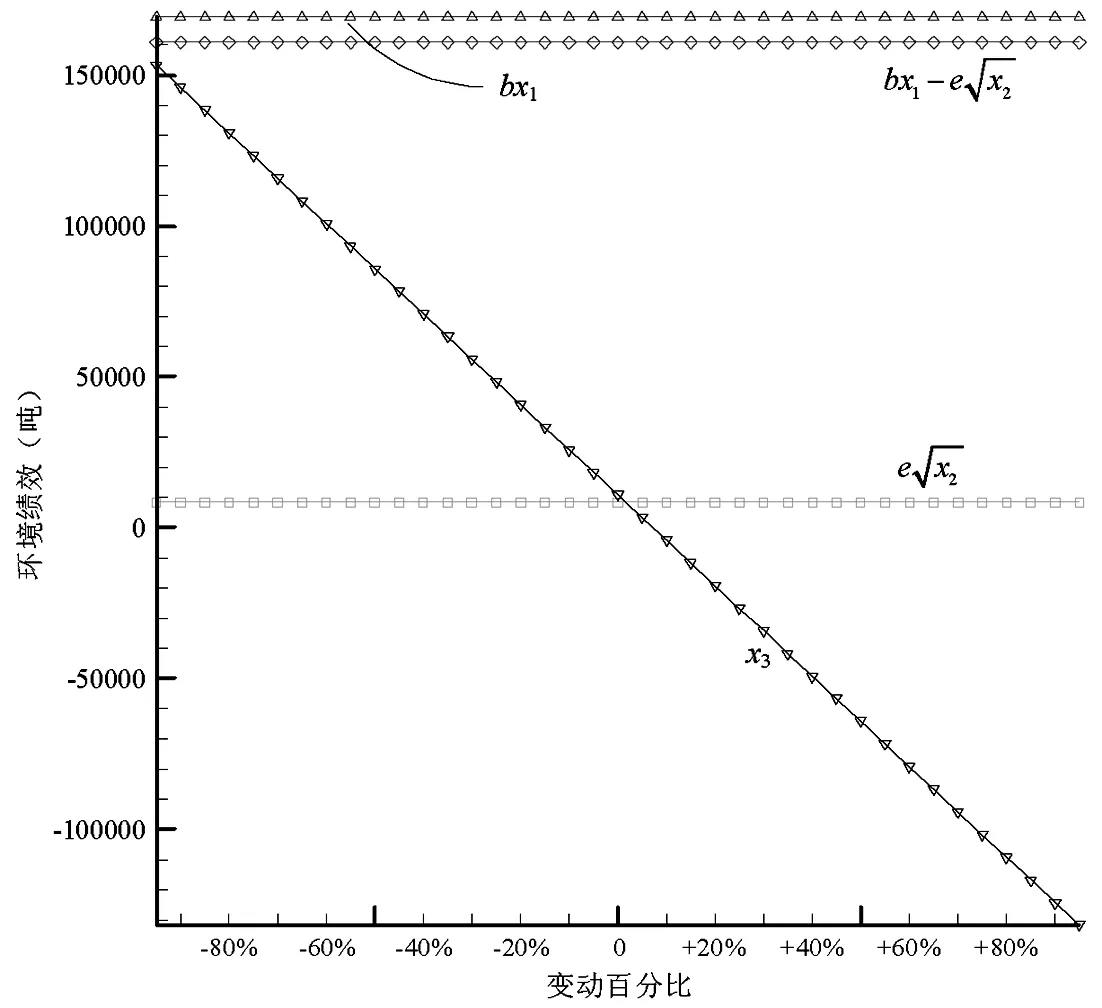
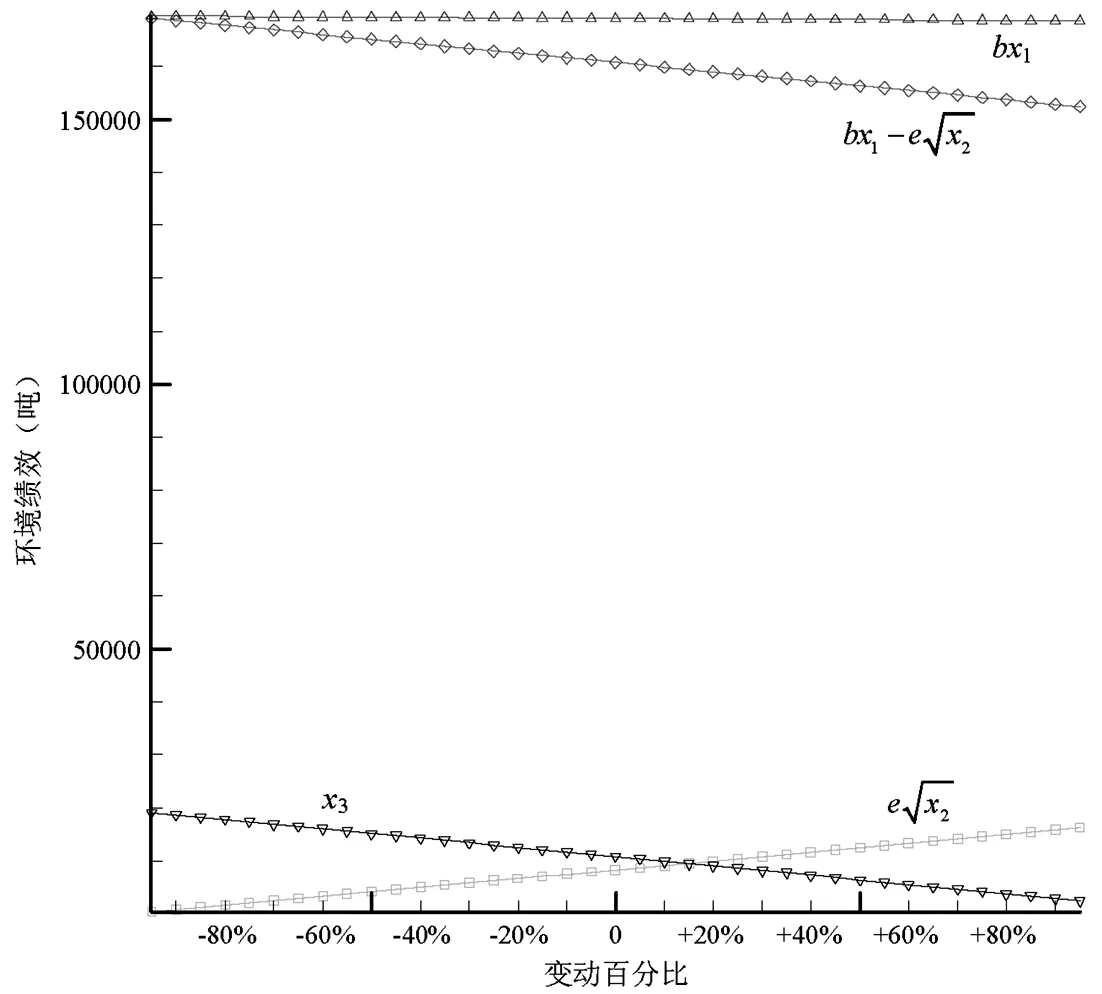
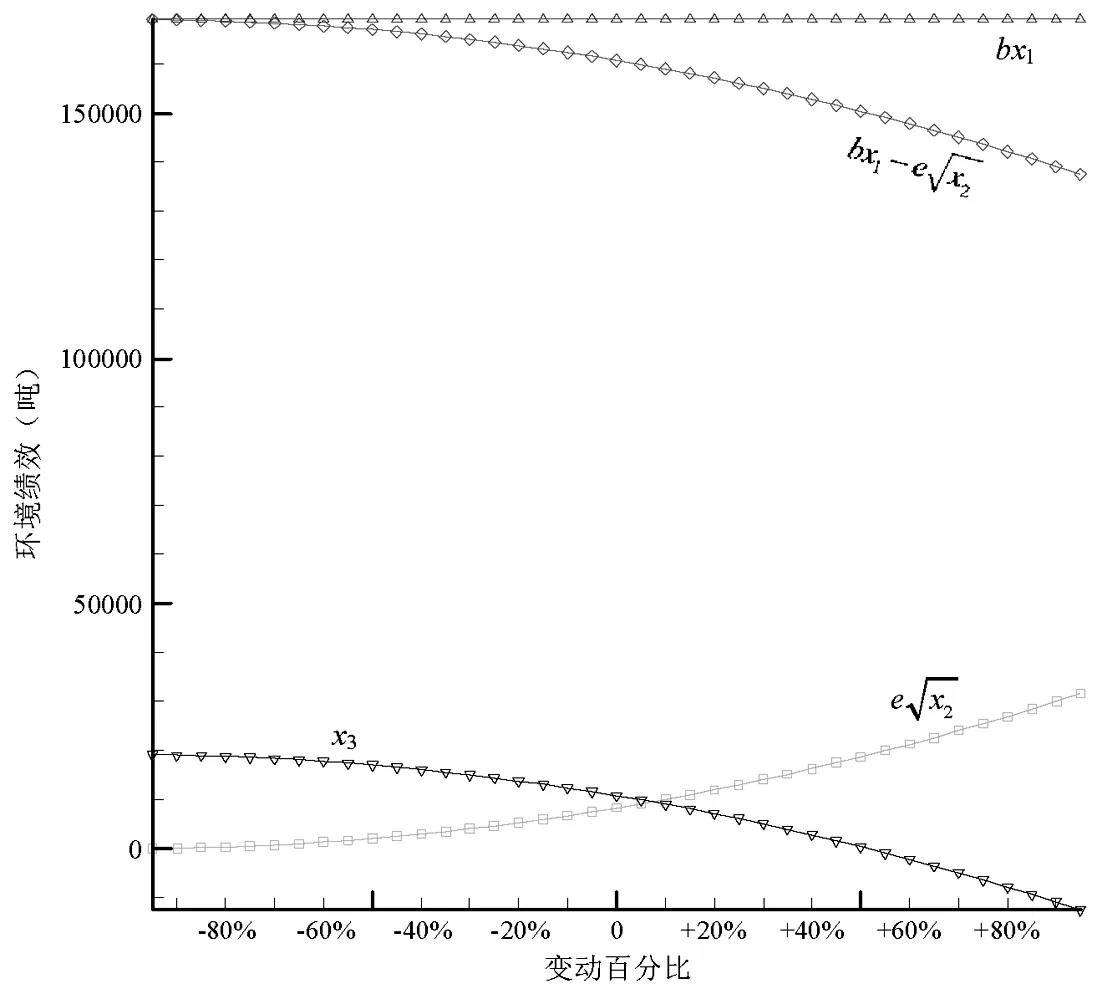
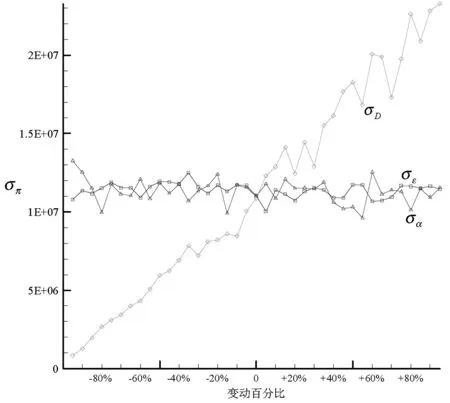
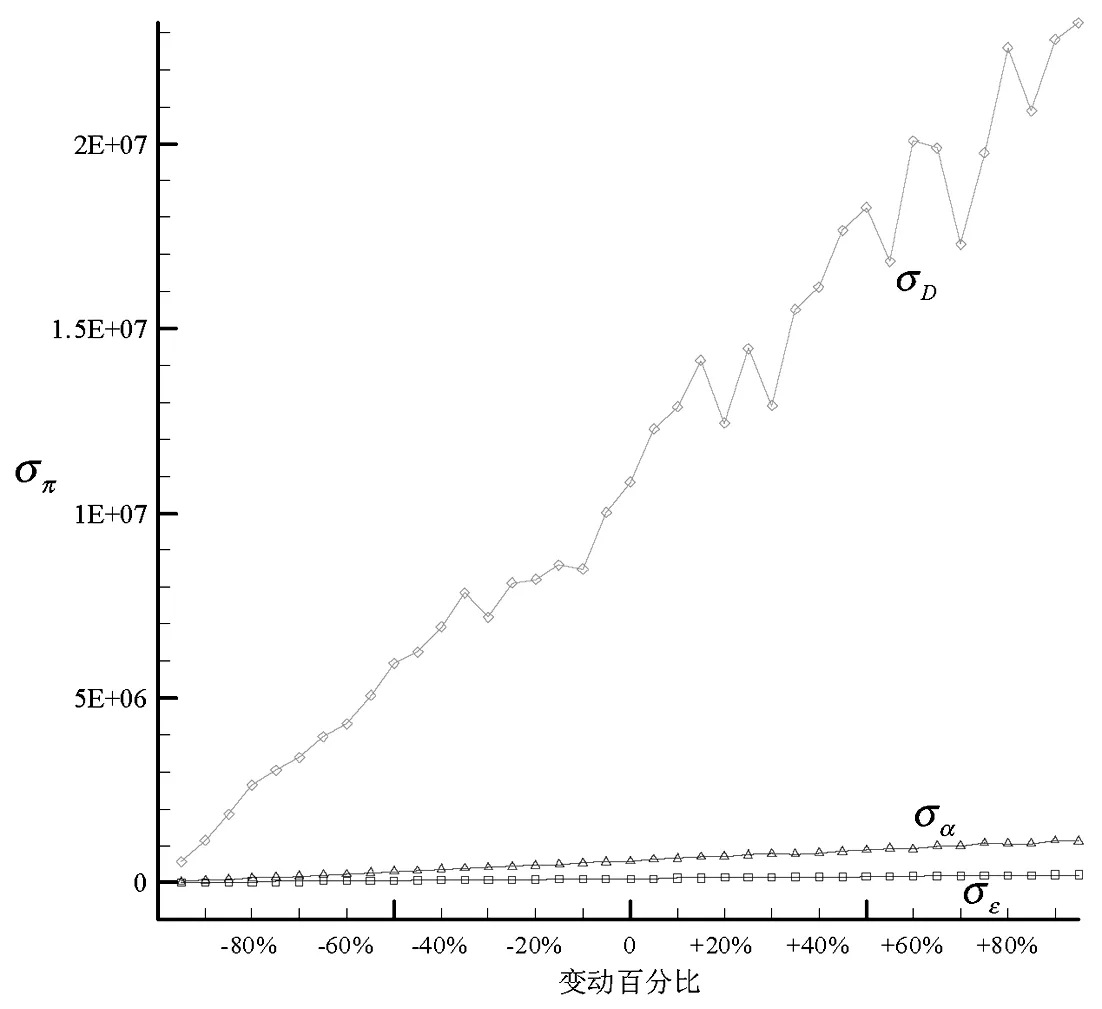
命题3可由式(2)、(3)、(4)得证。由式(2)、(3)、(4)还可看出,当企业实际碳排放量超过碳配额时(A>Q),碳配额越大,企业从碳市场购买的碳排放权(A 证明 由于概率分布函数的逆函数是递增函数,因此命题4可由式(3)得证。 从命题4可以看出,随着产品价格和缺货成本的上升,企业应该扩大产量;随着库存成本、碳价、单位产品碳排放和制造成本的上升,企业应该减少产量。与传统生产相比,C&T条件下,碳价和单位产品碳排放对企业产量有重要影响:随着碳价和单位产品碳排放的上升,企业碳排放成本(p2b)上升,因此企业将减少产量降低排放,以在经济绩效和环境绩效之间取得合理平衡。 命题5可由式(4)得证。从命题5可以看出,随着绿色改进系数上升,绿色改进难度下降,企业将加大绿色改进投入以减少碳排放量;随着碳价上升,企业也将加大绿色改进投入以减少购碳成本(如果实际排放超过碳配额),或者增加售碳收益(如果实际排放低于碳配额)。由于本模型中的碳价包含碳市场交易成本,因此,政府可将碳市场交易成本作为促进企业实施绿色改进措施的一项策略,增加碳市场交易成本有利于生产过程的绿色改进(E上升),进而降低企业的实际排放(A=T-E下降),减少对环境的污染。但碳价的上升同时也可能导致企业购碳量的下降(x3=A-Q减小),进而抑制碳市场的发展。因此政府应该根据碳市场调节的实际需要,制定合理的碳市场交易成本。 命题6可由命题(4)和命题(5)得证。从命题6可以看出,碳价和绿色改进系数上升,都将促进企业减少排放,进而减少对环境的影响。 命题7 与非C&T环境相比(不存在绿色改进投入和碳权交易),C&T环境下企业最优产量更低,碳排放量更小。 证明 非C&T环境下,假设企业不存在绿色改进和碳权交易,此时企业的利润函数π′没有C2和C1两项,即π′=R-C1-C4-C5,则期望利润为: (10) 从命题7可以看出,在C&T环境下,企业将减少产量以减小排放成本,同时实施绿色改进以获取更多排放权,因此,C&T环境有利于企业减少碳排放。 命题8 企业期望利润是绿色改进系数e和碳配额Q的递增函数,是单位产品碳排放b的递减函数。 命题8可由式(2)得证。绿色改进系数上升将导致绿色投资回报增加,碳配额上升可促使企业减少碳权购买量(或增加碳权出售量),因此均会带来企业利润的增加。单位产品碳排放增大则将导致排放成本上升,进而减少企业利润。 表1 基准模型参数列表 图1展示了各参数变动时的期望利润变化情况,可以看出,期望利润与碳配额Q和绿色改进系数e正相关,与单位产品碳排放b和碳价p2负相关,这与命题3和命题8相符。但碳配额Q和单位产品碳排放b对利润的影响更大,而绿色改进系数e和碳价p2对利润的影响则更不敏感。图2显示了期望利润函数的三维图形,可以看出其严格上凸;相对于绿色改进投资而言,产量对期望利润的影响更为显著。图3显示了单位产品碳排放b变动下的环境绩效:随着单位产品碳排放的增加,企业排放上升,碳权交易逐渐由出售变为购买,而且购买量不断增加。图4显示碳配额Q对绿色改进和碳排放无影响,但随着碳配额的增加,企业购买的碳权减少(出售的碳权增加)。图5和图6表明,随着碳价p2和绿色改进系数e的增加,绿色改进量上升,碳排放和购碳量下降。 图1 不同参数变动下的期望利润 图2 期望利润函数的三维图形 图3 单位产品碳排放b变动下的环境绩效 图4 碳配额Q变动下的环境绩效 图5 碳价p2变动下的环境绩效 图4 绿色改进系数e变动下的环境绩效 为分析需求风险、碳市场风险和绿色改进风险对产量和利润的影响,本文采用仿真平台Arena©构建仿真模型进行蒙特卡洛模拟[31],系统参数(如需求标准差)作为仿真模型的输入,系统绩效(如期望利润)作为仿真模型的输出,1000次独立重复的随机抽样评价问题的一组解,得到基准模型的期望利润为137418349(元),95%置信区间半长为695808(元),置信区间半长约为均值的0.5%,该置信区间能够较好涵盖理论值(137495376元)。因此,后续的仿真实验随机抽样次数均设为1000。图7所示为仿真模型逻辑图,首先产生逻辑实体,然后将随机需求、碳价波动和绿色改进风险(随机抽样)赋值给实体属性,接着统计排放和成本相关的绩效,图中的VBA模块用于记录每次抽样产生的企业利润,1000次抽样完成即统计平均利润、标准偏差等指标。由公式(2)和(3)可以看出,需求风险(用标准偏差σD衡量)对产量和期望利润有影响(见表2),但碳价波动σα和绿色改进风险σε只影响利润波动σπ。表2可见随着需求风险σD的上升,最优产量和期望利润都将减小。图8显示了需求风险、碳价波动和绿色改进风险对利润波动的影响,当σD变化时,先改变最优产量再做仿真实验以获取利润波动σπ;当σα和σε变化时则无需改变最优产量(因为只有σD对产量有影响)。图8(a)显示的是多源风险条件下的结果,即当某一风险大小发生变化时(如σD),其它风险仍然存在(如σα和σε均大于0);图8(b)显示的是单一风险条件下的结果,即当某一风险大小发生变化时(如σD),不存在其它风险的影响(如σα和σε均为0)。图8表明:风险越大,利润波动也越大,但需求波动对利润波动的影响更为显著。 图7 仿真模型逻辑图 表2 需求风险对产量和期望利润的影响 图8(a) σD 、σα和σε对σπ的影响(多源风险) 图8(b) σD、σα和σε对σπ的影响(单一风险) C&T环境给排放企业带来了新的巨大挑战。本文提出一个多元非线性优化模型分析C&T环境下的企业最优产量,并在绿色改进和碳权交易之间有效权衡。我们的主要研究结论如下:(1)企业新的生产条件是p1+l>v+p2b,即在C&T环境下,企业除了考虑传统的产品价格、变动成本等要素之外,还必须考虑排放成本(p2b)的影响;(2)C&T环境下,企业的最优产量如式(3)所示,它是产品价格和单位缺货成本的递增函数,是单位库存成本、碳价、单位产品碳排放和单位变动成本的递减函数;与非C&T环境相比,新的最优产量更低,实际排放下降;(3)最优绿色改进投资如式(4)所示,它与碳价的平方和绿色改进系数的平方成正比;(4)碳配额影响企业利润和碳权交易量,但不影响最优产量和最优改进投入,因此政府不能把碳配额作为调整企业产量和促进企业绿色改进的手段;(5)企业实际碳排放量是碳价和绿色改进系数的递减函数;企业期望利润则是绿色改进系数和碳配额的递增函数,是单位产品碳排放的递减函数;(6)需求风险的增加将导致最优产量和期望利润下降;需求风险、碳市场风险和绿色改进风险都将导致利润波动,风险越大利润波动越高,但需求风险对利润波动的影响更为显著。 中的有关模型类似,本文所提优化模型也存在一定局限,如假设排放企业会在期末出售所有剩余排放权。因此,考虑碳权存储的多阶段决策问题将是未来的一个重要研究方向。 参考文献: [1] IPCC. Climate change 2007: the physical science basis[R]. Cambridge University Press, UK. 2007: 1-18. http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-spm.pdf. [2] Zhang Y G. Supply-side structural effect on carbon emissions in China[J]. Energy Economics, 2010, 32(1): 186-193. [3] He Y Y, Wang L Z, Wang J H. Cap-and-trade vs. carbon taxes: a quantitative comparison from a generation expansion planning perspective[J]. Computers and Industrial Engineering, 2012, 63(3): 708-716. [4] Zhu B Z, Wei Y M. Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology[J]. OMEGA-The International Journal of Management Science, 2013, 41(3): 517-524. [5] 刘铁男.中国能源发展报告2011[R].北京:经济科学出版社,2011. [6] 深圳市发展和改革委员会.深圳碳交易试点总体框架研究报告(深圳碳交易试点研究报告之一)[R].深圳排放权交易所内部资料,2011. [7] Rao R V. Evaluation of aggregate risk in green manufacturing[A]. Decision making in the manufacturing environment: using graph theory and fuzzy multiple attribute decision making methods[C]. London, UK: Springer Series in Advanced Manufacturing, Springer-Verlag London Limited, 2007, Part 2: 277-283. [8] Kennedy P W. Optimal early action on greenhouse gas emissions[J]. Canadian Journal of Economics, 2002, 35(1): 16-35. [9] Wang M X, Wang M R, Wang S Y. Optimal investment and uncertainty on China's carbon emission abatement[J]. Energy Policy, 2012, 41(2): 871- 877. [10] 张跃军,魏一鸣.国际碳期货价格的均值回归:基于EU ETS的实证分析[J].系统工程理论与实践,2011,31(2):214-220. [11] Yi W J, Zou L L, Guo J, Wang K, Wei Y M. How can China reach its CO2intensity reduction targets by 2020? A regional allocation based on equity and development[J]. Energy Policy, 2011, 39(5): 2407-2415. [12] James B, Chen Y. Allocation and leakage in regional cap-and-trade markets for CO2[J]. Resource and Energy Economics, 2012, 34(4): 647- 668. [13] 许士春,何正霞,魏晓平.资源消耗、污染控制下经济可持续最优增长路径[J].管理科学学报,2010,13(1):20-30. [14] 杨玉香,周根贵.EPR下供应链网络报废产品排放内生污染税模型[J].管理科学学报,2011,14(10):67-76. [15] Hua G W, Cheng T C E, Wang S Y. Managing carbon footprints in inventory management[J]. International Journal of Production Economics, 2011, 132(2): 178-185. [16] Bouchery Y, Ghaffari A, Jemai Z, Dallery Y. Including sustainability criteria into inventory models[R]. Research Report, 2011: 2-26. [17] Chen X, Benjaafar S, Elomri A. The carbon-constrained EOQ[J]. Operations Research Letters, 2013, 41(2): 172-179. [18] 何大义,马洪云.碳排放约束下企业生产与存储策略研究[J].资源与产业,2011,13(2):63- 68. [19] Rong A Y, Lahdelma R. CO2 emissions trading planning in combined heat and power production via multi-period stochastic optimization[J]. European Journal of Operational Research, 2007, 176(3): 1874-1895. [20] Catalao J P S, Mariano S J P S, Mendes V M F, Ferreira L A F M. Short-term scheduling of thermal units: emission constraints and trade-off curves[J]. European transactions on electrical power, 2008, 18(1): 1-14. [21] Absi N, Dauzère-Pérès S, Kedad-Sidhoum S, Penz B, Rapine C. Lot-sizing with carbon emission constraints[A]. Proceedings of the first International Workshop on Lot Sizing[C]. Gardanne, France, August 25th-27th, 2010: 46- 48. [22] Kockar I, Conejo A J, McDonald J R. Influence of the emissions trading scheme on generation scheduling[J]. Electrical Power and Energy Systems, 2009, 31(9): 465- 473. [23] 魏一鸣,王恺,凤振华,从荣刚.碳金融与碳市场——方法与实证[M].北京:科学出版社,2010. [24] Chang N B, Qi C, Islam K, Hossain F. Comparisons between global warming potential and cost-benefit criteria for optimal planning of a municipal solid waste management system[J]. Journal of Cleaner Production, 2012, 20(1): 1-13. [25] 郑燕,方军,牛东晓.电厂排放管理决策的动态分析方法[J].电网技术,2006,30(22):49-53. [26] 杜少甫,董骏峰,梁樑,张靖江.考虑排放许可与交易的生产优化[J].中国管理科学,2009,17(3):81- 86. [27] 桂云苗,张廷龙,龚本刚.CVaR测度下考虑碳排放的生产策略研究[J].计算机工程与应用,2011,47(35):7-10. [28] Jonathan M B, Adrian S L. Convex analysis and nonlinear optimization: theory and examples(Second Edition)[M]. New York: Springer-Verlag, 2006. [29] Ruszczynski A. Nonlinear optimization[M]. Princeton University Press, 2006. [30] 马玉莲,忻仕海.碳足迹评价方法学在PVC产品中的应用[J].氯碱工业,2011,47(1):1- 6. [31] Kelton W D, Sadowski R P, Sturrock D T. Simulation with arena[M]. McGraw Hill Higher Education: New York, 2009. Decision Analysis of Generating Companies with Stochastic Demands under C&T Environment XIONG Yi1,2, CHEN Zhi-min2, HUO Jia-zhen1, PAN Yan-chun2, ZHOU Ming2 (1.SchoolofEconomicsandManagement,TongjiUniversity,Shanghai200092,China; 2.CollegeofManagement,ShenzhenUniversity,Shenzhen518060,China) Cap-and-trade(C&T)brings new challenges to the operational decisions of generating companies. A nonlinear optimization model is proposed in this paper to analyze the optimal production quantity under C&T environment, and balance between green improvement and carbon trade. Our model captures the marginal decreasing effect and risk of green improvement as well as the stochastic demands and carbon price. The optimal solution and its existence condition for generating companies are given via theoretical analysis. Our research results can be summarized as follows. Compared with traditional environment without C&T, the new optimal production quantity and the actual emission under C&T environment are much lower. Emission allowance has an important impact on expected profit and carbon trade, while it has nothing to do with the optimal production quantity and optimal investment of green improvement. The larger the carbon price and green improvement coefficient are, the more the generating companies invest on green improvement to reduce carbon emission. The expected profit increases with the increase of green improvement coefficient and emission allowance, while it decreases with the increase of emission per unit product. Numerical experiments validate our theoretical model and its analytical results. Monte Carlo simulation reveals that demand risk, green improvement risk and carbon price fluctuation have an important impact on expected profit, while demand risk has a more significant impact on the fluctuation of profit. cap-and-trade; stochastic demand; green improvement; nonlinear optimization; decision analysis 2014- 09-24 国家自然科学基金资助项目(71101094,71172057,71272089,71472126);广东省自然科学基金资助项目(S2012010008868) 陈智民(1962-),男,博士,教授,研究方向:运营管理;熊轶(1976-),女,博士研究生,研究方向:交通与运作管理、收益管理。 F272;X321 A 1007-3221(2015)06- 0025- 09 10.12005/orms.2015.0192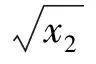
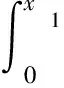
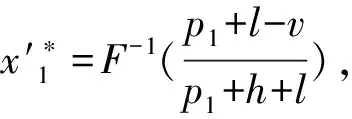
3 数值分析和蒙特卡洛模拟


4 结论

