基于风险偏好与满意度的区间值合作对策
邹正兴, 李登峰, 何 云
(1.北京理工大学 管理与经济学院,北京 100081; 2.福州大学 经济与管理学院,福建 福州 350108; 3.燕京理工学院 数学实验室,河北 三河 065201)
基于风险偏好与满意度的区间值合作对策
邹正兴1,3, 李登峰2, 何 云3
(1.北京理工大学 管理与经济学院,北京 100081; 2.福州大学 经济与管理学院,福建 福州 350108; 3.燕京理工学院 数学实验室,河北 三河 065201)
研究区间Shapley值一般是以超可加区间值合作对策或凸区间值合作对策为前提,但这限制了区间Shapley值的适用范围。本文以区间数的接受指标及局中人对风险的偏好水平为基础,提出了局中人满意度的概念,并利用满意度对区间值合作对策进行了探讨。通过计算区间值合作对策的局中人与联盟对其区间Shapley值的满意度,来判断区间Shapley值是否被局中人或联盟接受,形成的联盟是否稳定,拓展了区间值合作对策Shapley值的适用范围。同时,得到了当区间值合作对策满足一定条件时满意度的一些性质。
区间值合作对策;区间Shapley值;接受指标; 区间数;风险偏好;满意度
0 引言
合作对策在经济管理中的应用越来越广泛,Shapley值是合作对策最常用的解之一。由于现实的不确定性,联盟收益往往不是一个精确的数,而是一个变化的范围,由此区间值合作对策成为一个重要的研究热点。Wang[1]提出了区间值合作对策的概念,并利用基于区间中点的区间数排序方法,给出了区间Shapley值的公理体系,证明了区间Shapley值的唯一性。Branze[2]通过研究银行破产对策,建立了具有区间收益的模糊合作对策模型,并提出了类似于Shapley值的解。Alparslan等[3~7]研究了区间值合作对策的性质,对区间Shapley值进行了公理化定义,并对集合形式解的概念进行了拓展。Mallozzi等[8]以三角模糊数为基础,给出了模糊区间值合作对策的截对策的定义,并研究了其区间核心的性质。Graziano等[9]将区间值合作对策拓展到多准则区间值合作对策,并对其核心进行了讨论。张强等[10]指出了区间值合作对策的区间核心非空的充要条件为凸区间值合作对策,同时也说明不能直接将经典合作对策的结论套用到区间值合作对策。高作峰等[11]将局中人对收益的偏好关系引入到区间值合作对策,并对其区间核心进行了研究。
在研究区间Shapley值时,一般是将区间值合作对策限制为超可加区间值合作对策或凸区间值合作对策,可以得到较好的结果与性质,但是这大大限制了区间Shapley值的适用范围。针对此问题,本文以文献[12]中区间数的偏好关系为基础,根据文献[13]的研究思路,提出了基于区间数接受指标与局中人风险偏好的满意度的概念,利用满意度分析区间值合作对策的分配,并据此判断分配是否合理、联盟是否稳定,可极大地拓展区间Shapley值的适用范围。
1 预备知识
1.1 区间数及其运算
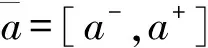
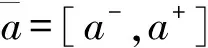
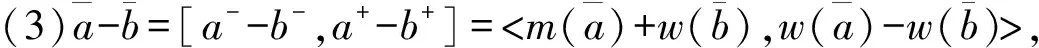
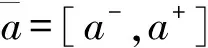
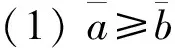
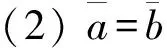
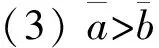
1.2 区间值对策的概念及其区间Shapley值
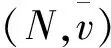
设(N,v)为经典合作对策,如果∀S,T⊆N,且S∩T=,满足v(S)+v(T)≤v(S∪T),则称(N,v)为超可加合作对策。如果满足v(S)+v(T)≥v(S∪T),则称(N,v)为次可加合作对策[14]。
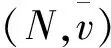
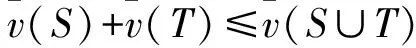
(1)
显然,超可加区间值合作对策等价于区间数左、右端点构成的对策是超可加的;次可加区间值合作对策等价于区间数左、右端点构成的对策是次可加的。很多文献[1~9]是基于此进行研究的。
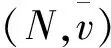
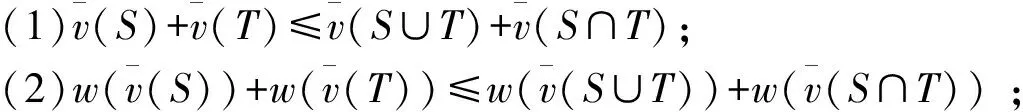
则称(N,Vw)为凸区间值合作对策。
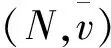
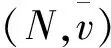
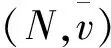
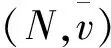

(2)
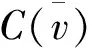
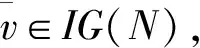
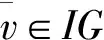
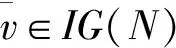
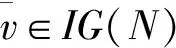
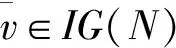
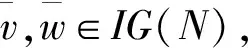
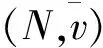
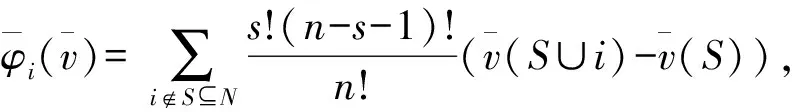
(3)
其中,s,t分别为联盟S,T中局中人的个数。
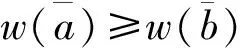
因为超可加区间值合作对策的区间Shapley值满足个体合理性,凸区间值合作对策的区间Shapley值包含在区间核心中[4,5],因此在研究区间Shapley值时,一般是将区间值合作对策限制在超可加区间值合作对策或凸区间值合作对策上。
从理论上讲,区间值合作对策中局中人或联盟获得的收益可能是收益区间中的任意值,那么,区间值合作对策只要存在选择对策满足超可加性,稳定的联盟就可能形成,就可以讨论区间Shapley值。更一般地,就算区间值合作对策所有的选择对策都不是超可加对策(显然不是超可加区间值合作对策),其区间Shapley值也存在,而且可能每个局中人或联盟都接受该分配方案。
根据定义9,该区间Shapley值包含在区间核心中,即满足个体合理性与集体合理性,故任意局中人及联盟均接受此分配方案。为拓展区间Shapley值的适用范围,本文不是去寻找区间值合作对策满足的条件,而是先利用公式(3)计算出区间值合作对策的区间Shapley值,然后再判断该区间Shapley值是否被所有局中人或联盟接受。
2 区间数的序关系的定义及性质
两个区间具有包含、相交、重叠等多种不同情形。定义3仅以区间的两个端点为基础建立区间数的序关系,具有一定的局限性。为能比较任意两个区间数的大小或序关系,下面对区间数的序关系进行探讨。
2.1 区间数的接受指标
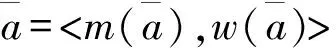
(4)
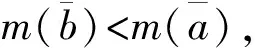
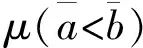
2.2 基于风险偏好的满意度
根据接受指标的概念,可以将区间数的中点理解为收益的期望,将区间数的区间半径理解为不确定性,即区间中点越大,期望收益就越大,区间半径越小,收益就越确定。因为区间数是一类特殊的模糊数,其模糊性决定了局中人对区间数的态度往往不是严格的接受或拒绝,而是取决于区间数之间的序关系以及局中人对风险的态度。下面在接受指标的基础上,结合文献[15]的定义方法,考虑局中人具有风险态度水平时区间数的序关系。
局中人(或决策者)对风险的态度不同可以分为风险厌恶型、风险中立型、风险偏好型等。对于风险厌恶型局中人,当区间数的均值相同时,认为区间半径越短越好。本文从风险厌恶型局中人的角度给出如下假设:
(1)收益越大越好,即区间数的区间中点越大越好;
(2)收益值越精确越好,即区间数的区间半径越短越好;
(3)当收益越大,但是对应的不确定性也越大时,局中人会综合考虑收益与风险;
(4)风险厌恶型局中人认为上述假设(2)比假设(1)重要。
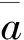
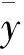
(5)
为简化问题,本文以联盟收益为局中人决策的参考点。
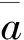
(6)
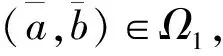

表1 语言变量与风险偏好水平的对应关系表
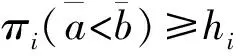
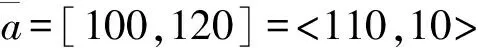
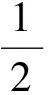
3 基于满意度的区间值合作对策
利用满意度的概念,下面定义区间值合作对策中局中人或联盟对区间Shapley值的满意度。
(7)
设局中人的最低满意度向量为h=(h1,h2,…,hn)∈Rn,且hi∈(0,1],则当πi≥hi(∀i⊆N)时,任意局中人i都接受区间Shapley值,即对单个局中人来说,区间Shapley值是合理的分配方案。
(8)
对其他分配的满意度可以类似地定义。如果有局中人或联盟S的满意度不存在或者小于其最低满意度,则拒绝该分配方案。
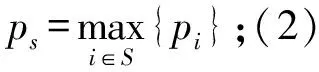
当πS≥hS(∀S⊆N))时,则大联盟N可以形成。否则,若存在T⊆N,使得πT 在例1中,若局中人对风险均持中立态度,即pi=1(i=1,2,3)。利用式(7)和式(8)算出各局中人与联盟满意度为:π1=1,π2=1,π3=1,π{1,2}=1,π{1,3}=1,π{2,3}=1,π{1,2,3}=1。故该区间Shapley值,被所有的局中人或联盟接受,是合理的分配,且大联盟也是稳定的。 尽管(N,vm)的Shapley值不一定包含在其核心中,但可以通过计算满意度,分析分配不合理或联盟不稳定的内在原因。 (9) 其中点对策(N,vm)的Shapley值为: 其半径对策(N,vw)的Shapley值为: 证毕。 注2 如果半径对策的Shapley值为负数,说明对应的区间Shapley值的左端点大于右端点,表明局中人的边际贡献随着对策值的增大反而相对降低,因而边际收益逐渐减小。但是在分析其满意度时需将其调整为正常的区间数,则负数变为其绝对值。例如<4,-2>=[6,2]调整为[2,6],即为<4,2>。即在分析区间数的满意度时,区间Shapley值的区间半径是半径对策的Shapley值的绝对值。 (1)中点对策(N,vm)为超可加对策; (2)半径对策(N,vw)为次可加对策,且满足vw(S)≤vw(T)(∀S⊆T); 则区间值合作对策中任意局中人对其区间Shapley值的满意度均为1。 证明 (1)当中点对策(N,vm)为超可加对策,即对任意的S,T∈P(N),且S∩T=Ø,有vm(S∪T)≥vm(S)+vm(T)。 当且仅当vm(S∪i)=vm(S)+vm(i)(∀S⊆Ni)时,等号成立。 (2)当半径对策(N,vw)为次可加对策,即对任意的i∉S∈P(N),有vm(S∪i)≤vm(S)+vm(i),则 又因为对∀S⊆T都有vw(S)≤vw(T),得到vw(S∪i)≥vw(S),故有φi(vw)≥0。 此命题的逆命题不成立。命题1中,半径对策的次可加性条件可以减弱。若去掉半径对策(N,vw)为次可加对策的条件,即为Alparslan[3~6]研究区间Shapley值的前提。由命题1可知,该区间Shapley值不一定会被局中人所采纳,故本文是Alparslan研究基础上的进一步探讨。同时,当区间半径退化为0时,此对策退化为超可加对策,其Shapley值满足个体合理性,此性质与经典合作对策的性质[14]具有一致性。 注3 利用中点与半径进行区间数减法运算时,区间半径可以为负。现实意义见注2。 故x是(N,vm)满足有效性的分配。 (10) 即分配x满足集体合理性。如果S是单个局中人,则说明分配x满足个体合理性。 (11) 所以 (12) 证毕。 如果所有局中人与联盟的满意度存在,则需(N,vm)是平衡对策。但平衡对策检验较复杂,命题2的结论更为直观。 引理2[14]当合作对策为凸对策时,其Shapley值包含在核心中。 (1)vm(S)+vm(T)≤vm(S∪T)+vm(S∩T); (2)vw(S)+vw(T)≥vw(S∪T)+vw(S∩T); (3)vw(S)≤vw(Q)(∀S⊆Q); 证明 条件(1)说明(N,vm)为凸对策,由引理2可知,其Shapley值Φ(vm)=(φ1(vm),φ2(vm)…,φn(vm))∈Rn包含在其核心中,即满足 (13) (14) 对于(N,vw)与(N,v),由Shapley的可加性公理,可知 φi(vw)=d-φi(v) (∀i∈N) (15) 由式(14)和(15)可知 (16) 又根据条件(3),可知 φi(vw) ≥0,(∀i∈N) (17) (18) 命题3是区间值合作对策的区间Shapley值为可行的分配方案,且联盟是稳定的必要条件。同时,也说明了区间值合作对策的中点对策是凸对策,联盟也不一定是稳定的。 根据定义4,可知该对策不是超可加区间值合作对策。首先,利用式(3)计算各局中人的区间Shapley值: 然后,利用式(7)计算各局中人的满意度: 即单个局中人均对其分配的区间Shapley值接受。 最后,联盟的风险偏好水平按照取大的方法,利用式(8)计算各联盟的满意度: 即联盟{1,2}、{1,3}、{2,3}的满意度均为1,因为1>0.5,故不会有局中人离开大联盟。 综合上述分析可知,该区间值合作对策是稳定的,且区间Shapley值是合理的分配。 利用式(3)计算各局中人的区间Shapley值: 利用式(7)和(8)计算各局中人或联盟的满意度: 由上述计算可知,虽然局中人1、2以及联盟{1,3}、{2,3}对区间Shapley值的满意度均为1,即接受该分配。但是,局中人3的满意度不存在,说明局中人3不接受其分配到的区间Shapley值,其宁愿选择单干得到收益[20,50],即该区间Shapley值不是可行的分配方案。同时,联盟{1,2}的满意度也不存在,说明尽管局中人1与2接受该区间Shapley值,但是该区间Shapley值却不能满足联盟{1,2}的要求,即{1,2}单独结盟会得到更好的结果,所以稳定的大联盟也不会形成。 区间Shapley值的研究一般是限制在超可加区间值合作对策或凸区间值合作对策。本文利用局中人对区间Shapley值的满意度,拓展了区间Shapley值的适用范围。首先,以区间数接受指标为基础,并考虑风险偏好对局中人的影响,从风险厌恶型局中人的角度,定义了区间数的满意度的概念。然后,以满意度为处理区间数的工具,分析区间值合作对策的局中人对区间Shapley值的满意度,将满意度作为分配是否合理,联盟是否稳定的依据。最后,得到满意度在一些特殊情形时具有的某些性质。本文的方法为处理区间值合作对策提供了一种新思路,对不确定性决策与对策具有一定的参考价值。基于区间数的序关系,分析区间值合作对策联盟的形成以及各联盟之间的相互作用将是以后的研究重点。 [1] Shunmin Wang. Interval computations for fuzzy relational equations and cooperative game theory[D]. North Carolina State University, 2002. [2] Branzei R, Dimitrov D, Tijs S. Shapley-like values for interval bankruptcy games[J]. Economics Bulletin, 2003, 3: 1- 8. [3] Alparslan G S Z, Miquel S, Tijs S. Cooperation under interval uncertainty[J]. Mathematical Methods of Operations Research, 2009, 69(1): 99-109. [4] Alparslan G S Z, Branzei R, Tijs S. Convex interval games[J]. Journal of Applied Mathematics and Decision Sciences, 2008, 37: 1-18. [5] Branzei R, Alparslan G S Z, Tijs S. Cooperative interval game: a survey[J]. Central European Journal of Operations Research, 2010, 18(3): 397- 411. [6] Alparslan G S Z, Branzei R, Tijs S. The interval shapley value: an axiomatization[J]. Central European Journal of Operations Research, 2010, 18(2): 131-140. [7] Alparslan G S Z, Branzei O, Branzei R, Tijs S. Set-valued solution concepts using interval-type payoffs for interval games[J]. Journal of Mathematical Economics, 2011, 47(4-5): 621- 626. [8] Mallozzi L, Vincenzo Scalzo, Tijs S. Fuzzy interval cooperative games[J]. Fuzzy Sets and Systems, 2011, 165(1): 98-105. [9] Graziano P, Lucia P. Interval values for multicriteria cooperative game[J]. AUCO Czech Economic Review, 2010, 4(2): 189-200. [10] Xuan Zhao, Qiang Zhang. A further discussion on cores for interval-valued cooperative game[J]. Knowledge Engineering and Management: Advances in Intelligent Systems and Computing, 2014, 214: 673- 682. [11] 高作峰,邹正兴,马栋. 局中人具有偏好关系的区间值合作对策问题[J].系统科学与数学,2013,33(6):528-540. [12] Atanu S, Tapan K P. Fuzzy preference ordering of interval numbers in decision problems[M]. Berlin Heidelberg: Springer-Verlag, 2010. [13] Deng-Feng Li. Decision and game theory in management with intuitionistic fuzzy sets[M]. Berlin Heidelberg: Springer-Verlag, 2014: 319-356. [14] Branzei R, Dimitrov D, Tijs S. Models in cooperative game theory[M]. Berlin Heidelberg: Springer-Verlag, 2008. [15] Deng-Feng Li, Jiang-Xia Nan, Mao-Jun Zhang. Interval programming models for matrix games with interval payoffs[J]. Optimization Methods and Software, 2012, 27(1): 1-16. [16] Zimmermann H J. Fuzzy set theory and its application [M]. Boston: Kluwer Academic, 1991. Interval-valued Cooperative Games Based on Risk Preferences and Satisfaction ZOU Zheng-xing1,3, LI Deng-feng2, HE Yun3 (1.SchoolofManagementandEconomics,BeijingInstituteofTechnology,Beijing100081,China; 2.SchoolofEconomicsManagement,FuzhouUniversity,Fuzhou350108,China; 3.LaboratoryofMathematical,YanchingInstituteofTechnology,Sanhe065201,China) The study of interval Shapley value is usually based on superadditive interval-valued cooperation games or convex interval-valued cooperative games, limiting the scope of the application of the interval Shapley value. Based on acceptability index——the fuzzy preference ordering for interval and the intensities of risk preferences for players, we discuss the concept of the players with degrees of satisfaction. In this paper, we find that the degree of satisfaction plays a key role of analyzing the interval-valued cooperative games. By calculating the degrees of satisfaction with the allocation for interval-valued cooperative games, we find it obvious to determine whether the allocation, including the interval Shapley value, is reasonable. And we can judge whether the coalitions of players who coordinate their actions is stable by using the degrees of satisfaction. The basis of this method is an extension of the application of the interval Shapley value. Furthermore, we get some useful properties when the interval-valued cooperative game is at particular situations. interval-valued cooperative games; interval shapley value; acceptability index;interval number; risk preferences; degrees of satisfaction 2013-12- 05 国家自然科学基金重点项目(71231003);国家自然科学基金资助项目(71171055,71071018,71371030) 邹正兴(1989-),男,湖北天门人,博士研究生,研究方向:对策论及其应用;李登峰(1965-),男,广西人,博士(后) ,博士生导师,教授,主要从事模糊决策与对策的理论及应用。 O225 A 1007-3221(2015)06- 0034-10 10.12005/orms.2015.0192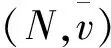
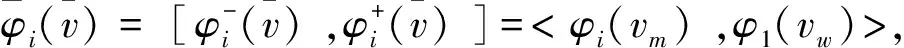
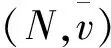
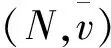
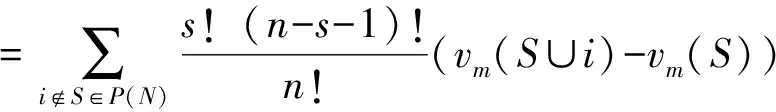
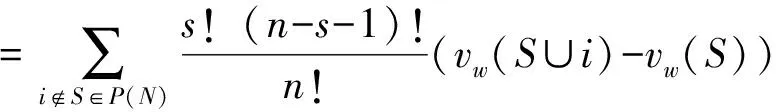
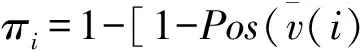
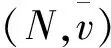
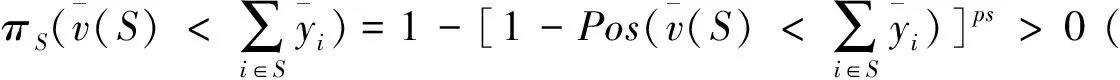
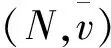
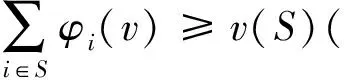
4 举例:满意度在区间值合作对策中的应用
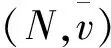
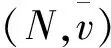
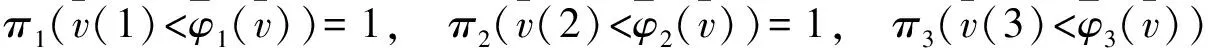
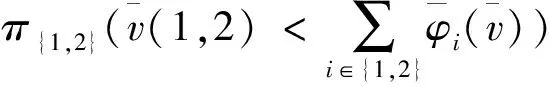
5 结论

