排序对策的一个新的收益分配准则
周意元, 张 强
(1.北京理工大学 管理与经济学院,北京 100081; 2.三峡大学 理学院,湖北 宜昌 443002)
排序对策的一个新的收益分配准则
周意元1,2, 张 强1
(1.北京理工大学 管理与经济学院,北京 100081; 2.三峡大学 理学院,湖北 宜昌 443002)
针对一个机器的排序问题,给出了排序问题中成本增加量的表达式,提出了收益分配的不小于成本增加量准则。针对一类特殊的排序问题,给出一个符合不小于成本增加量分配准则的解,并证明了它满足有效性,哑元性和单调性。结合一个算例,对本文的提出的方法进行了分析验证。
合作对策;排序问题;收益分配准则;核心
0 引言
排序对策(sequencing game)是Curiel等[1]为了利用合作对策的方法解决如下的排序问题而提出来的。有限个局中人在一个机器前按初始顺序排队等待服务,每位局中人有一个工件需要在这个机器上处理。局中人在等待他的工件被处理完的过程中有成本,这些成本与完工时间成正比,队列的总成本是各局中人成本之和。可以通过调整局中人的顺序使总成本最小,相对于初始顺序时的总成本,减少的总成本可以认为是所有局中人合作而产生的收益,那么这些收益该如何在所有局中人之间分配?文献[1]提出了收益分配的EGS准则(equal gain splitting rule), 它将相邻局中人通过交换顺序而减少的成本平均分配给这两位局中人,EGS准则所产生的解属于排序对策的核心。
此后,学者们对排序问题和排序对策中的工件处理时间、机器数量、初始顺序等进行了拓展研究[2~6]。由于合作对策的核心具有较好的性质且凸对策和均衡对策的核心非空,因此这些研究工作的重点是相应对策的凸性或均衡性。也有学者研究排序问题和排序对策的收益分配准则,如GS准则(gain splitting rule)[7]、退出单调准则[8]等。
在排序问题和排序对策中,当总成本减少时,有些局中人的成本会减少,但是有些局中人的成本反而会增加,这些成本增加量就是他们的损失。如果按照某个收益分配准则,一位局中人得到的分配小于他的成本增加量,这样的分配准则是不够合理的。
本文主要考虑排序对策的收益分配准则,提出了不小于成本增加量的分配准则,满足这个准则的分配都属于排序对策的核心,同时它能保证每个局中人得到的分配不小于他的成本增加量。针对一类特殊的排序问题,给出了一个满足不小于成本增加量分配准则的解,它满足有效性、哑元性。
1 排序问题和排序对策
排序问题中,所有局中人的集合记为N={1,2,…,n},局中人i的工件也记为i,σ0是队列的初始顺序,σ0(i)=j表示初始时局中人i排在第j位或工件i排在第j位,工件i的处理时间pi>0,排在队列首位的工件从时刻t=0开始处理。局中人i在顺序σ0下的成本C(σ0,i)=αit,其中t是工件i在顺序σ0下的完成时间,αi≥0是局中人的单位时间成本。则排序问题可以记为(N,σ0,p,α),其中向量p=(pi)i∈N,α=(αi)i∈N。
记号P(σ,i)={j∈N|σ(j)<σ(i)}表示在顺序σ下,比工件i先处理的工件构成的集合,F(σ,i)={j∈N|σ(j)>σ(i)}表示在顺序σ下,比工件i后处理的工件构成的集合。
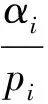
对排序问题(N,σ0,p,α),总有一个合作对策(N,ν)与之对应,称为排序对策[1]。为了确定排序对策中联盟S⊆N的收益值ν(S),需要讨论哪些顺序对联盟S是可接受的。对联盟S⊆N内的局中人调整顺序时,不能影响NS中局中人的成本。
定义1[1]如果对任意的j∈NS,工件处理顺序σ满足P(σ0,j)=P(σ,j),则称σ对联盟S是可接受的,∑S表示联盟S所有可接受的顺序构成的集合。
排序对策(N,ν)定义如下,
(1)
它表示在可接受的顺序下,联盟S中的局中人合作最多能节约的成本。显然ν({i})=0,而
(2)
其中τ是大联盟的最优顺序。
定义2[1]对所有i,j∈S和k∈N,如果由σ0(i)≤σ0(k)≤σ0(j)可以得到k∈S,则称联盟S是连通的。
对于连通的联盟S,表达式(1)可以改写为
(3)
其中gij=max{0,αjpi-αipj}表示当σ0(i)=σ0(j)-1时, 局中人i和j交换顺序后减少的成本。对非连通的联盟T,有ν(T)=∑S∈Tσ0ν(S),其中Tσ0是由T的最大连通子集构成的集合,“最大”是指连通子集增加任何一个不属于该子集的元素后就不是连通的。
为了把所有局中人合作产生的收益ν(N)在这些局中人之间分配,学者们提出了EGS准则[1]和GS准则[7]。在EGS准则下,局中人i得到的分配是
而按照GS准则,局中人i得到的分配为
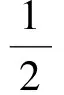
合作对策(N,ν)的核心C(ν)={x∈Rn|x(N)=ν(N),x(S)≥ν(S),∀S⊂N},由EGS准则和GS准则产生的解都属于排序对策的核心[1,7]。
2 不小于成本增加量的分配准则
在排序问题(N,σ0,p,α)中,若σ0(i)=σ0(j)-1和ui
对给定的i∈N,令H(u,i)={j∈N|uj>ui}表示紧迫性指数大于ui的局中人构成的集合,L(u,i)={j∈N|uj 对于局中人i和j,如果j∈H(u,i)∩F(σ0,i),根据最优顺序的紧迫性指数递减原则,i和j需要交换顺序,即i往后移动,j往前移动,则i的成本是增加的,j的成本是减少的。如果j∈L(u,i)∩P(σ0,i),则i往前移动,j往后移动,那么i的成本是减少的,j的成本是增加的。如果j∈H(u,i)∩F(σ0,i),则反之有i∈L(u,j)∩P(σ0,j)。为了行文方便,将H(u,i)∩F(σ0,i)记作H∩F,将L(u,i)∩P(σ0,i)记作L∩P。 从初始顺序σ0变为最优顺序τ后,局中人i增加的成本ΔCi为 当ΔCi>0时,局中人i的成本是增加的;ΔCi<0时,他的成本实际是减少的。 定义3 对策(N,ν)是与排序问题(N,σ0,p,α)对应的排序对策,不小于成本增加量分配准则是:分配x∈Rn满足(1)x∈C(ν), (2)xi≥ΔCi,i∈N。 所有满足不小于成本增加量分配准则的解记作G(N,σ0,p,α),即 G(N,σ0,p,α)={x∈Rn|x∈C(ν),xi≥ΔCi,i=1,2,…,n} 显然有G(N,σ0,p,α)⊆C(ν)。 对于排序对策,虽然它的核心一定存在,但是满足不小于成本增加量分配准则的解不一定存在,下面针对一类特殊的排序对策,给出一个满足不小于成本增加量分配准则的解。 证明 对连通的联盟S, 所以fλ,σ0(S)≥ν(S)。当S=N时,fλ,σ0(N)=ν(N)。对于非连通的联盟T有 如果对所有i∈N和j∈H∩F都有2ui 从而 因此fλ,σ0≥ΔCi。由以上证明过程有fλ,σ0∈G(N,σ0,p,α),证明完毕。 Hamers等[7]提出了排序问题(N,σ0,p,α)解的三个性质:有效性、哑元性和单调性。 设排序问题(N,σ0,p,α)的最优顺序是τ,向量x是它的解。 (1)有效性:x(N)=C(σ0,N)-C(τ,N)。 (2)哑元性:如果存在k∈N使P(σ0,k)=P(τ,k),则xk=0,即如果队列中没有局中人与k交换顺序,则k得不到任何分配。 (3) 单调性:假设(N,σ1,p,α)也是排序问题,其中σ0(i)=σ0(j)-1,σ1(i)=σ0(j),σ1(j)=σ0(i),而当k≠i,j时,σ1(k)=σ0(k)。对(N,σ0,p,α)的任意解x∈Rn,则一定存在(N,σ1,p,α)的解y∈Rn,使下面两个结论之一成立。 (i)当k≠i,j时,xk=yk,而xi≥yi和xj≥yj; (ii)当k≠i,j时,xk=yk,而xi≤yi和xj≤yj。 定理2 对策(N,ν)是与排序问题(N,σ0,p,α)对应的排序对策,如果对所有i∈N和j∈H(u,i)都有2ui 证明 (1)因为fλ,σ0∈G(N,σ0,p,α)⊆C(ν),有效性是显然的。 (2)如果P(σ0,k)=P(τ,k)且队列的最优顺序是τ,则P(σ0,k)=P(τ,k)=H(u,k),F(σ0,k)=F(τ,k)=L(u,k),所以H(u,k)∩F(σ0,k)=Ø,L(u,k)∩P(σ0,k)=Ø。因此 (3)由于(N,σ1,p,α)是排序问题,且k≠i,j时σ1(k)=σ0(k)成立,则对所有的k∈N{i,j},有P(σ0,k)=P(σ1,k),F(σ0,k)=F(σ1,k),而 根据单调性定义中的条件有P(σ0,i)=P(σ1,j)和F(σ0,j)=F(σ1,i),为了行文方便,记P=P(σ0,i)=P(σ1,j),F=F(σ0,j)=F(σ1,i)。 由于当i∈N和j∈H(u,i)时,2ui (a)如果ui>uj,则ui>2uj和αipj-2αjpi≥0,而 (b)如果ui 排序问题(N,σ0,p,α),其中N={1,2,3,4,5},初始顺序σ0(i)=i,p=(3,2,2,7,3),α=(6,9,4,2,3)。 局中人的紧迫性指数大小关系为u2>u1=u3>u5>u4,局中人1和3的紧迫性指数相等且初始时1排在3的前面,因此最优顺序中1也应该排在3的前面,最优顺序τ为τ(1)=2,τ(2)=1,τ(3)=3,τ(4)=5,τ(5)=4. 从初始顺序调整为最优顺序后,局中人的成本增加量分别为ΔC1=12,ΔC2=-27,ΔC3=0,ΔC4=6,ΔC5=-21. 满足EGS准则的收益分配方案为EGS=(7.5,7.5,0,7.5,7.5)。 在调整队列顺序的过程中,没有局中人与3交换顺序,也就是说局中人3在此次合作中没有任何贡献,他得不到任何分配。成本增加的局中人1和4得到的分配都大于他们的成本增加量。 本文提出了不小于成本增加量的分配准则,满足这个准则的解能使局中人得到的分配不小于他的成本增加量。针对满足一定条件的排序问题,给出了一个满足不小于成本增加量分配准则的解,并证明了它具有良好的性质。 [1] Curiel I, Pederzoli G, Tijs S. Sequencing games[J]. European Journal of Operational Research, 1989, 40: 344-351. [2] Grundel S, Ciftci B, Borm P, Hamers H. Family sequencing and cooperation[J]. European Journal of Operational Research, 2013, 226: 414- 424. [3] Hamers H, Klijn F, Van Velzen B. On the convexity of precedence sequencing games[J]. Annals of Operations Research, 2005, 137: 161-175. [4] Van Velzen B. Sequencing games with controllable processing times[J]. European Journal of Operational Research, 2006, 172: 64- 85. [5] Slikker M. Balancedness of multiple machine sequencing games revisited[J]. European Journal of Operational Research, 2006, 174: 1944-1949. [6] Klijn F, Sanchez E. Sequencing games without initial order[J]. Mathematical Methods of Operations Research, 2006, 63: 53- 62. [7] Hamers H, Suijs J, Tijs S, Borm P. The split core for sequencing games[J]. Games and Economic Behavior, 1996, 15: 165-176. [8] Fernandez C, Borm P, Hendrickx R, Tijs S. Drop out monotonic rules for sequencing situations[J]. Mathematical Methods of Operations Research, 2005, 61: 501-504. [9] Smith W. Various optimizers for single-stage production[J]. Naval Research Logistic Quarterly, 1956, 3: 59- 66. A New Allocation Rule for Sequencing Games Coalition of Sequencing Games ZHOU Yi-yuan1,2, ZHANG Qiang1 (1.SchoolofManagementandEconomics,BeijingInstituteofTechnology,Beijing100081,China; 2.CollegeofScience,ChinaThreeGorgesUniversity,Yichang443002,China) One-machine sequencing situations and corresponding sequencing games are considered, the main aim is an allocation rule. The expression of the cost increment is presented. A new allocation rule is introduced, the payoff based on the rule is greater than or equal to the cost increment and belongs to the core of corresponding sequencing game. For a special class of sequencing situation, a solution is designed to compensate players for their losses firstly and allocate the remaining worth among the players secondly, it is proved that this solution satisfies the new rule and has the property of efficiency, dummy property and monotonicity. Meanwhile, a numerical example is studied. cooperative games; sequencing situation; allocation rule; core 2014- 04-21 国家自然科学基金资助项目(71371030,71071018,71201089);高等学校博士学科点专项科研基金资助项目(20111101110036);宜昌市科学技术研究与开发项目(A201230225) 周意元(1980-),男,讲师,博士研究生,主要研究方向:合作对策,决策理论和方法;张强(1955-),男,教授,博士生导师,研究方向:合作对策,决策理论和方法。 O225 A 1007-3221(2015)06- 0011- 05 10.12005/orms.2015.0190

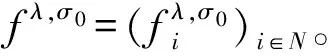
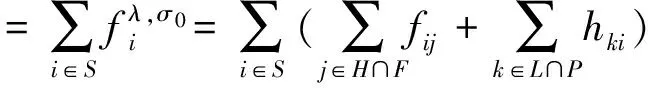
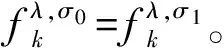
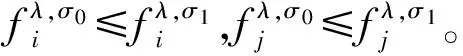


3 数值算例
4 结论

