需求依赖于服务水平的易变质品库存策略研究
段永瑞, 傅琼超, 李贵萍
(同济大学 经济与管理学院, 上海 200092)
需求依赖于服务水平的易变质品库存策略研究
段永瑞, 傅琼超, 李贵萍
(同济大学 经济与管理学院, 上海 200092)
本文研究需求依赖于上一周期服务水平、缺货时订单部分损失的两周期易变质品库存问题。分别考虑一次订货和多次订货两种情况,以平均利润最大化为目标构建库存模型,证明了模型解的存在性和唯一性,得到了最优库存服务水平和最优补货策略。最后,通过算例给出两个模型的应用,对重要参数进行了灵敏度分析,并且将两种模型的结果进行了对比分析。结果表明:订单损失率的增加会提高服务水平,但会使得利润降低;顾客期望服务水平的提高会降低第一阶段的服务水平,同时使利润减少;单位库存持有成本或变质率的增加会降低服务水平和平均利润。通常情况,企业通过多次订货能获得更大的利润,而只有当库存持有成本极小时,一次订购才能够获得更大的利润。同时,结果也表明:服务水平对库存策略有较大的影响,因此在进行库存决策时考虑服务水平具有重要的作用。
物流与供应链管理;库存模型;最优化;易变质品;需求依赖于服务水平
0 引言
随着经济全球化的发展,市场竞争环境越来越激烈,顾客对产品的要求越来越高。同时,随着科技的发展,越来越多的物品呈现出“变质”的特征,这里的“变质”指随着时间的推移,物品的价值发生耗损、物品的质量和数量发生损失等一系列现象,如生鲜食品的腐烂、电子产品的更新换代等。产品如果不能通过销售渠道迅速到达顾客手中,会由于变质、破损、新产品出现等原因,导致其价值将不断减少。由变质造成的损失越来越多,易变质品的库存优化也变得越来越重要。
20世纪60年代以来,易变质品的库存问题受到了广泛关注。Ghare和Scharder[1]研究了库存物品指数变质的库存控制系统。Chaudhuri和Chakrabarty[2]在模型中引入了具有很强普适性的三参数的Weibull函数来描述变质率,较好地模拟了物品变质的过程,并且研究了需求为线性的变质品库存问题。励凌峰等[3]在此基础上研究了有限时域内无限订货次数情况下的最优订购策略。Dye等[4]在变质率是时间的线性函数的前提下,建立了利润最大化的定价-库存模型,得到了最优的销售价格及订货批量。
需求率的假设是易变质品库存研究的一个关键因素。Ghosh和Chaudhuri[5]建立了需求率是时间的二次函数的易变质物品的库存模型。Chung等[6]研究了需求率与库存相关的易变质物品库存模型。Abad[7]建立了有限生产率且需求率由价格决定的允许缺货的EPQ模型。Teng和Chang[8]提出了需求同时与库存和价格相关的EPQ模型。这些易变质品库存模型假设需求率依赖于时间、价格和库存等,但都没有考虑服务水平对需求率的影响。事实上,商品在进入成熟期以后,顾客在购买商品时不仅仅考虑价格、商品的即时库存等要素,而且更加注重伴随购买行为所得到的服务,服务在顾客决策中已占据重要地位,如Schwartz[9]所述,“在非垄断市场上,顾客对于缺货的第一反应是,要么接受延迟交付,要么到别的供应商去购买。然而当顾客选择第二种行为时,供应商损失的不仅仅是一定的销售额,还有信誉的损失,并可能对未来产品的需求造成影响。” 在库存优化的研究中常用无缺货率(α-服务水平)和订单满足率(β-服务水平)来定义服务水平,因此Schwartz[9]所述的内涵即是服务水平可能对未来需求造成影响。Liu,Shang和Wu[10]在其模型中假设顾客决定是否转移需求到别的供应商由上一期需求是否满足来决定,但是模型中假设物品是不变质的。
由于产品的生产周期一般比较长,而随着科技的进步和市场竞争的加剧,产品的销售周期却越来越短,因此零售商在第一次订货之后,在产品的有限销售周期内可能仅有一次再订购的机会。本文基于这一背景,研究有限销售期内仅有两个补货周期的易变质品库存控制问题,假设两个补货周期相等,第一个周期的需求为常数,第二周期的需求依赖于第一周期的服务水平。分别考虑多次订购和一次订购两种情况,以平均利润最大化为目标函数建立各自的库存模型。对于多次订购的情况,假设系统允许缺货,并且对第二个周期末的缺货量采取期末一次性补货满足,通过分析得到系统的最优服务水平存在且唯一的条件,并得到了相应的最优订购量;对于一次订购模型,系统不允许缺货,此时求解得到其最优补货策略。最后通过数值分析给出了两个模型的应用,分别对几个主要参数进行了灵敏度分析,并且结合数值算例对两种模型进行了比较分析。
1 假设与符号
本文主要研究需求依赖于上一周期服务水平的两个周期的易变质品库存策略。下面首先给出构建模型所用到的相关假设和符号表示:
(1)T为补货周期,瞬时补货且补货提前期为0。
(2)I1(t)表示t∈[0,T)时刻的库存水平,I2(t)表示t∈[T,2T)时刻的库存水平。t1表示在第一个补货周期内库存水平为非负的时间段长度,T-t1则表示在第一个补货周期T内库存水平为负时的时间段长度。t2-T表示在第二个补货周期内库存水平为非负的时间段长度,2T-t2表示在第二个补货周期内库存水平为负的时间段长度。
(3)λ1和λ2分别表示第一和第二周期的服务水平,0≤λ1,λ2≤1,且λ1和λ2为决策变量。根据Sana, Goyal和Chaudhuri[11],本文采用不发生缺货的时间段在一个周期内所占的比例来表示系统的服务水平,因此,λ1=t1/T,λ2=(t2-T)/T。
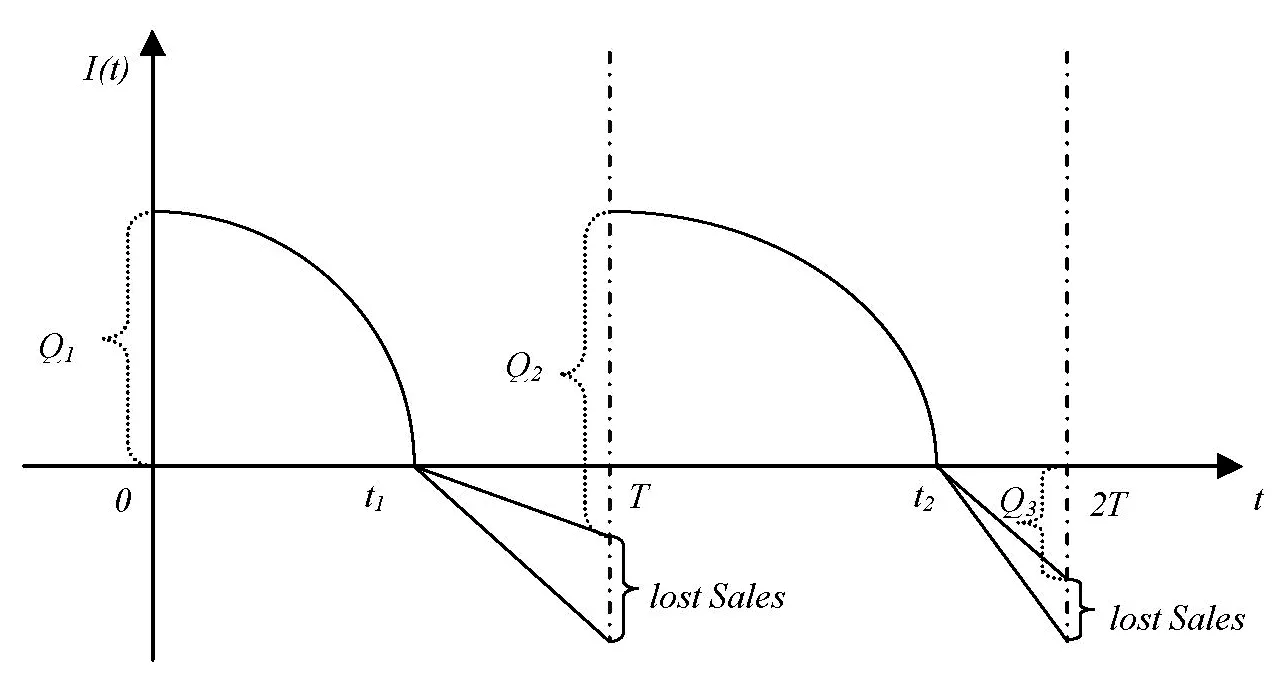
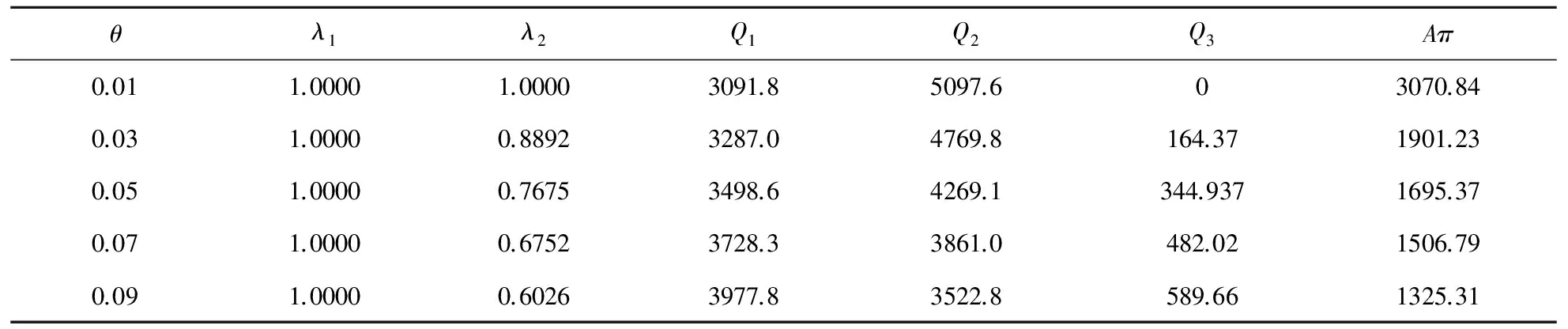
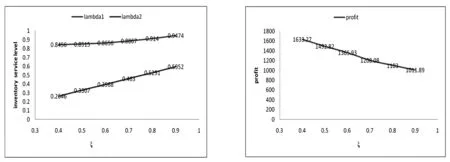
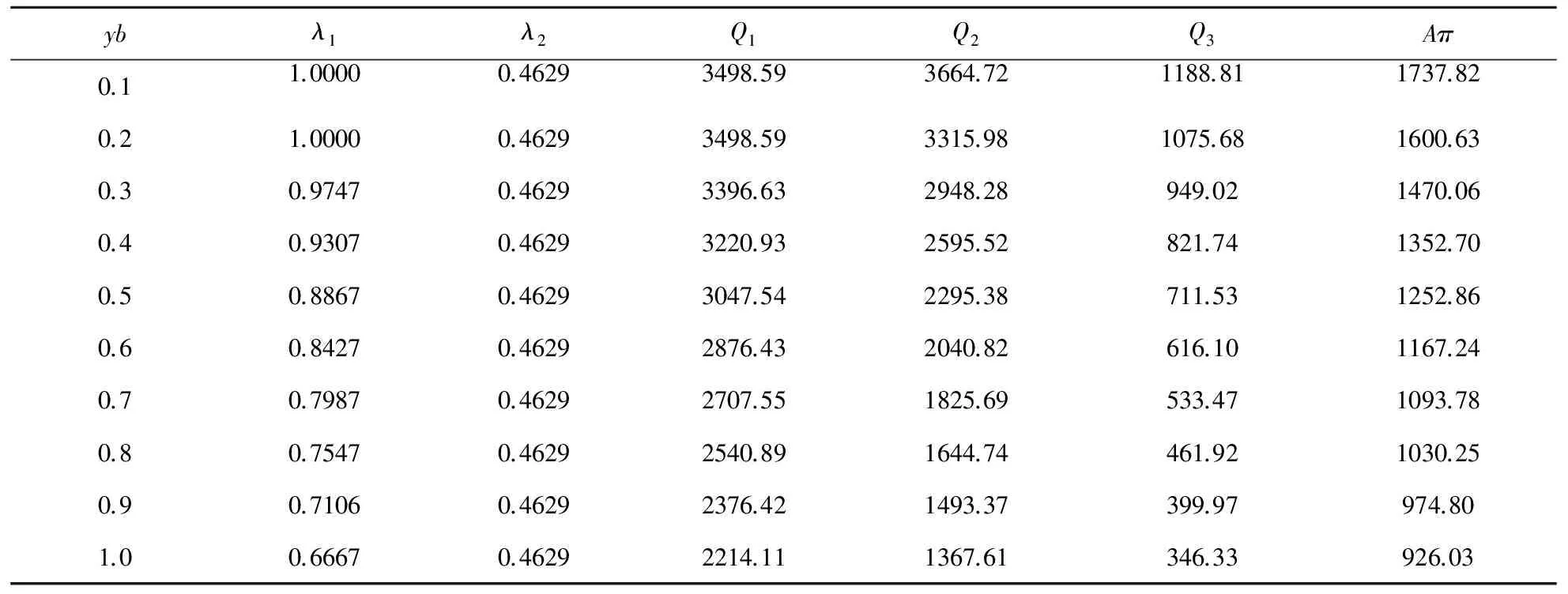
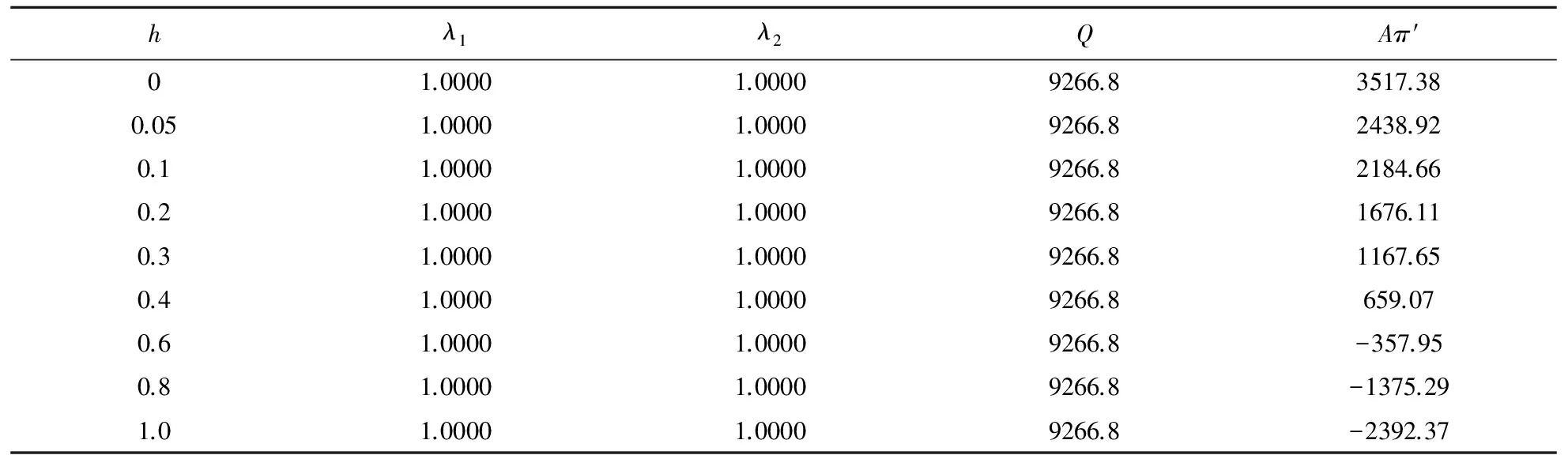
(4)D1和D2分别表示第一周期和第二周期的需求率,其中D1是常数,D2依赖于D1和λ1,且D2=e(λ1-b)·D1,这里b为顾客期望服务水平,0 (5)θ表示物品变质率,0<θ<1为常数;p表示产品售价(常数);A表示每个补货周期的订购成本(常数);c表示单位货物的购买成本(常数);h表示单位货物单位时间的库存持有成本(常数);cd表示单位变质成本,即单位物品变质后的处理成本;R表示两个周期的总收入;Aπ表示系统的平均利润。本文考虑的成本包括订购成本、购买成本、库存持有成本、变质成本。 2.1 多次订货库存模型的建立与分析 在多次订货的模式下,假设企业在第一个周期开始、第二个周期开始及第二个周期结束时订三次货,分别为Q1,Q2和Q3,其中Q3仅用来满足第二周期期末的缺货量。两个周期的库存变化如图1所示(Dye and Ouyang[12])。假设缺货期间需求部分损失,损失率为ξ(0<ξ<1)。第一个周期期初,企业的补货量为Q1。在[0,t1]内,由于需求和物品变质,库存不断减少,并在t=t1时刻库存降为0。之后,在[t1,T)内,缺货发生且订单部分损失,损失的需求量为D1ξ(T-t1),未损失的订单D1(1-ξ)(T-t1)将在第二补货周期期初一次性满足。在第二周期期初,补货量为Q2,在[T,t2]内,由于需求和物品变质,库存不断减少,并在t=t2时刻库存为0。之后,在[t2,2T]内,缺货发生且订单部分损失,损失的需求量为D2ξ(2T-t2),在第二补货周期期末增加一次补货,补货量为Q3以满足未损失的订单D2(1-ξ)(2T-t2)。 所以,第一个周期库存变化可以用如下微分方程表示: (1) 且满足边界条件I1(t)=0。 求解式(1)得到 (2) 所以第一周期补货量 (3) 第二个周期库存变化可表示为以下微分方程: (4) 且满足边界条件I2(t2)=0。 求解式(4)得到 (5) 因此,第二周期期初补货量为 (6) 图1 多次订购模式下库存水平的变化趋势 第二周期期末补货量为 Q3=D2(1-ξ)(2T-t2)=D1e(λ1-b)(1-ξ)(2T-t2) (7) 两周期的总成本C由以下几个部分组成: (i)订购成本:3A (ii)购买成本:c×(Q1+Q2+Q3) 因此,总成本 两个周期的销售收入可以表示为 =pD1[(T-ξT+ξt1)+e(λ-b)(T-2ξT+ξt2)] 因此,企业的平均利润可以表示为 Aπ=(R-C)/2T 因此这个问题是通过选择合适的λ1和λ2使得平均利润最大,即: maxAπ (8) 由于直接对(8) 进行求解比较困难,考虑到θ、λ1-b比较小,本文采用泰勒展开的方法对(8)进行求解(见Roya and Chaudhurib[13]),进而得到问题(8)的近似最优解。由泰勒展式 eθt1=1+θt1+(θt1)2/2 (9) eθ(t2-T)=1+θ(t2-T)+θ2(t2-T)2/2 (10) e(λ1-b)=1+(λ1-b)+(λ1-b)2/2 (11) 将式(9)~(11)代入,简化得 (12) (13) (14) 解得 (15) 证明 由0≤λ1≤1和0≤λ2≤1, (16) 进一步得出0≤λ2 下面证明解的存在唯一性: 4.2.2 推进产品提质增效,提高产品竞争力 一是应进一步加强甘薯品种改良、运输、贮藏、加工等领域的科技研发力度,改进生产工艺,降低各环节原料损耗,降低生产成本,提高出品率和生产效率等.二是应通过加快甘薯相关产品标准制定、监督与实施,规范甘薯淀粉原料市场,严厉打击各种违规掺杂廉价淀粉,以次充好的情况,严格控制甘薯淀粉产品的铝含量,保障甘薯加工产品品质,以符合目的地的质量要求.三是应当转变发展思路,走优质优价之路,开拓中高端国际市场,加强中国甘薯产品品牌建设,打造优质产品形象,提高产品附加值.从降低生产成本、提高产品品质和提高产品附加值3个方面,提高甘薯及其加工产品利润水平与国际竞争力. =0 设H表示Aπ(λ1,λ2)的海塞矩阵,则 (17) 证明 由于T<(p-c)ξ/(cθ+h+cdθ),λ1∈[0,1] 有 (18) (19) >(p-c)(2+2λ1-b+ξ-3ξλ1)D1/4 >0 (20) 注 由命题2,如果系统的补货周期较短,则企业全部满足顾客需求(不缺货)是最优的策略。 (21) (22) 由(3)、(6)、(7),可得最优补货量为别为: (23) 由于本文在求解的过程中采用了泰勒展式,因此上文得到的解析解仅是模型的近似最优解,第三部分的数值分析中我们将给出与应用数值分析方法得到的解的对比分析。 图2 一次订购模式下库存水平的变化趋势 2.2 一次订货库存模型的建立与分析 一次订货模式的库存变化如图2所示。假设两个周期中企业在第一周期期初订购足够多的货物Q来满足第一周期和第二周期的需求,两个周期均不发生缺货,两个周期的库存服务水平λ1=1,λ2=1在[0,T]内,由于需求和物品变质,库存不断减少,在[T,2T]内由于第一周期的服务水平对第二周期的需求有影响,所以在t=T时刻需求发生变化。 所以,系统库存变化可以用如下的微分方程表示: (24) 并且满足边界条件I1(T)=I2(T),I2(2T)=0。 求解得到 (25) (26) 进而得到 Q=I1(0)=(D1+D2)(eθT-1)/θ (27) 两周期的总成本由以下几个部分组成: (i)订购成本A (ii)购买成本c×Q 因此,总成本 两个周期的销售收入可以表示为 因此,企业的平均利润可以表示为 Aπ′ =(R′-C′)/2T 本节主要通过算例分析库存服务水平对系统最优策略的影响,分别讨论多次订购和一次订购模式下的最优解,并进行参数灵敏度分析。此外,对比分析了多次订购和一次订购的适用条件。各参数取值分别为p=10元/件,c=5元/件,h=0.05元/件/天,D1=500件/天,A=200元/次,θ=0.05,cd=0.2元/件,顾客期望服务水平b=0.5,补货周期T=6天,订单损失率ξ=0.7。 3.1 多次订购库存模型算例 当其他参数不变,h,θ,ξ,b变化时的结果见表1~表3以及图4~图5: 由表1容易看出,随着单位库存持有成本h的增加,两周期的服务水平和期初订购量(Q1和Q2)先保持不变然后逐渐减小,平均利润一直保持递减趋势。当h比较小时,第二周期期末的补货量Q3=0,随着h的增加Q3先逐渐增大然后又逐渐减少。当库存持有成本非常小时,企业选择在期初多订货,满足全部的需求来提高利润。当单位库存持有成本增大时,企业为了减少总库存持有成本,会相应减少持有库存的时间,延长缺货时间,因此库存服务水平降低,并且第一周期服务水平降低引起第二周期需求减少,最终导致平均利润减少。由表2容易看出随着变质率的增大,第一周期和第二周期期初的订购量减少,第二周期期末的订购量增加,系统平均利润降低。 表1 单位持有成本h对最优策略的影响 表2 变质率θ对最优策略的影响 图3 ξ对服务水平的影响 图4 ξ对平均利润的影响 从图3和图4可以看出,当缺货造成的订单损失率变大时,两周期的服务水平都增大,两次期初的订购量也增加,而第二周期期末补货量(Q3)呈递减趋势,企业的平均利润也逐渐减少。 表3 顾客期望服务水平b对最优策略的影响 由表3容易看出,第二周期的服务水平不随顾客期望服务水平的变化而变化,这是由于本文的第二周期是最后一个周期,因此企业在决定第二周期的服务水平时没有考虑未来需求。从表3可以得到,当顾客的期望服务水平提高时,由于企业第一周期的服务水平没达到顾客心中的期望值,导致第二周期需求减少,从而使得利润降低。同时从计算结果可以看出,第二周期的服务水平明显低于第一周期的,这是由于第一周期的服务水平会影响到第二周期的需求,而本文中第二周期是最后一个周期,因此在第二周期企业从利润最大化的角度进行决策,对服务水平的考虑较少,因此第二周期的服务水平普遍较低。这同时也说明,顾客期望服务水平是企业在进行库存决策时必须要考虑的非常重要的因素。 由于本文第二节的多次订购模型得到的解析解是近似最优解,下图是运用迭代方法直接求解与本文得到解析解的对比分析图: 图5 对比分析-h变化 图6 对比分析-θ变化 图7 对比分析-ξ变化 由图5~图7的比较结果可以看出,本文得到的解析解与应用迭代法求解得到的结果差别不大,误差在可接受的范围内,基本在1%上下浮动。因此,本文得到的解析解可以作为模型的近似最优解。 3.2 一次订购库存模型算例 当其他参数不变,h,θ变化时的结果见表4~表5: 由表4容易看出,随着单位持有成本的增大,平均利润逐渐减少,当单位持有成本较大时(h>0.4),平均利润小于0,企业面临亏损。这是由于在期初一次订购大量货品造成库存成本和变质成本变大,使得利润减小甚至出现亏损。由表5 我们可以得到,随着变质率的增大,期初订购量增加,而平均利润逐渐减少。当变质率较大时(θ>0.05), 企业的平均利润小于0。这也是由于库存成本和变质成本的增加使得利润减小。 表4 单位持有成本h对最优策略的影响 表5 变质率θ对最优策略的影响 3.3 多次订购与一次订购的比较 观察表1和表4,我们可以得到,只有当单位持有成本极小(接近0)时,一次订购模型的平均利润才会大于多次订购模型,一旦单位库存持有成本大于0.05时,多次订购模型的平均利润大于一次订购模型。由表2和表5容易看出,多次订购模型的平均利润比一次订购模型的平均利润大得多。 因此,其他参数相同时,只有当单位库存持有成本极小(接近0)时,企业选择一次订购,即在第一周期期初订购大量的货物来满足两周期的需求;否则,企业选择多次订购能获得更大的利润。 本文研究了需求依赖于上一周期服务水平的两周期易变质品库存策略。假设第二周期的需求依赖于第一周期的库存服务水平,允许缺货且缺货时订单部分损失。考虑一次订货和多次订货两种情况,分别以平均利润最大化为目标构建库存优化模型,给出模型最优解存在和唯一的充分条件。最后通过算例分析分别对多次订购和一次订购库存模型进行了验证,并且对参数进行了灵敏度分析,得到以下主要结论:(1)单位库存持有成本h增加时:无论是多次订购还是一次订购,系统平均利润均减小;多次订购情况下,两周期的服务水平和期初订购量都随着h的增大而减小;一次订购情况下,期初订购量不受h的影响,但是系统平均利润逐渐减少甚至会面临亏损。(2)当单位库存持有成本不是极小(接近0)时,企业选择多次订购能获得更大的利润;只有当单位库存持有成本极小(接近0)时,企业选择一次订购获得的利润更大。(3)对于多次订购模型,当缺货造成的订单损失率变大时,两周期的服务水平都将增大,两周期期初订购量也将增加,而第二周期期末补货量将减小,企业的平均利润也减少。(4)对于多次订购模型,当顾客期望服务水平增大时,企业获得的平均利润减小,这是因为企业第一周期的服务水平没达到顾客心中的期望值,导致第二周期需求减少,结果使得利润降低,此时企业应采取提高第一周期库存服务水平的策略。 本文主要研究了两周期易变质品的库存优化问题,在后续的研究中将考虑n订购周期下,当期的需求受前一周期服务水平影响的库存问题。同时还可以尝试其他需求函数的库存优化问题,使得模型能更接近实际。 [1] Ghare P M, Scharder G P. A model for exponentially decaying inventory[J]. Ind Eng, 1963, 4:238 -243 [2] Chakrabarty T, Girl B C , Chauhurti K S. An EOQ model for items with Weilbull distribution deterioration, shortages and ternded demand an extension of philips model[J]. Computers Operation Reseaerh, 1998, 25: 649- 657 [3] 励凌峰,黄培清,骆建文.易腐物品的库存管理研究[J].系统工程,2004,123:25-30 [4] Dye C Y, Hsieh T P, Ouyang L Y. Determining optimal selling price and lot size with a varying rate of deterioration and exponential partial backlogging[J]. European Journal of Operational Research, 2007, 181: 668- 678 [5] Ghosh S K, Chaudhuri K S. An order-level inventory model for deteriorating item with weibull distribution deterioration, time-quadratic demand and shortages[J]. Advanced Modeling and Optimization, 2004, 6(1): 21-35 [6] Chung K J, Chu P, Lan S P. A note on EOQ models for deteriorating items under stock dependent selling rate[J]. European Journal of Operational Research, 2000, 124: 550-559 [7] Abad P L. Optimal pricing and lot-sizing under conditions of perishability, finite production and partial backordering and lost sale[J]. European Journal of Operational Research, 2003, 144: 677- 685 [8] Teng J T, Chang C T. Economic production quantity models for deteriorating items with price-and stock-dependent demand[J]. Computers & Operations Research, 2005, 32: 297-308 [9] Schwartz B L. A new approach to stockout penalties[J]. Management Science. 1966, 12:B538-B544 [10] Liu L, Shang W, Wu S. Dynamic competitive newsvendors with service sensitive demands[J]. Manufacturing Service Oper Management, 2007, 9(1): 84-93 [11] Sana S, Goyal S K, Chaudhuri K S. A production-inventory model for a deteriorating item with trended demand and shortages[J]. European Journal of Operational Research, 2004, 157: 357-371. [12] Dye C Y, Ouyang L Y. An EOQ model for perishable items under stock-dependent selling rate and time-dependent partial backlogging[J]. European J Oper Res, 2005, 163:776-783. [13] Roya T, Chaudhurib K S. A production-inventory model under stock-dependent demand, weibull distribution deterioration and shortage[J]. International Transactions in Operational Research, 2009, 16(3): 325-346. Optimal Inventory Policy for Perishable Items with Service-level-dependent Demand Rate DUAN Yong-rui, FU Qiong-chao, LI Gui-ping (SchoolofEconomicsandManagement,TongjiUniversity,Shanghai200092,China) This paper deals with two period inventory optimization problem for perishable items where the demand rate depends on the service-level of the previous replenishment cycle. Two scenarios are considered, namely, (1)the buyer order once and (2)the buyer order several times in the selling period. Two inventory models are proposed respectively by maximizing the average profit. In addition, we prove the existence and uniqueness of the optimal inventory service-level and ordering quantity. Finally, an example is presented and the sensitivity analyses on the parameters are conducted to illustrate the validity and the effectiveness of the proposed models. The results show that, in the first case, when the unit inventory holding cost or deteriorating rate increases, the average profit of the system will decrease. As the deteriorating rate increases, the ordering quantity will also increase. In the second case, when the unit inventory holding cost, the expected service-level of customers or the loss rate of order during the shortage increases, the inventory service-level and the average profit of the system will decrease. Only when the inventory holding cost is extremely small, is order once more profitable, so the buyer will usually choose to order several times to enhance the profit. The results also indicate that, service-level is an important factor that influence the inventory policy, and the enterprise should balance the service-level and profits. operational management; inventory model; optimization; perishable items; service-level-dependent demand rate 2012- 03- 01 国家自然科学基金项目(71371139,71002020);上海市浦江人才计划(PJ12069);上海市曙光人才计划项目(13SG24) 段永瑞(1975-),女,山西太原人,教授、博士,研究方向:供应链管理和服务运作管理。 F253.4 A 1007-3221(2015)06- 0065-11 10.12005/orms.2015.01972 模型的建立与分析
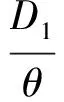
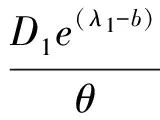
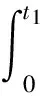
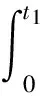
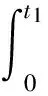
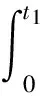


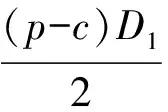
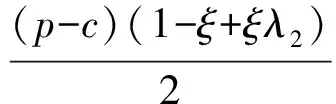
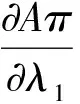
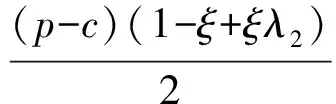



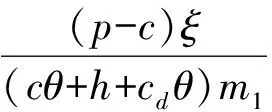
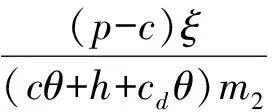


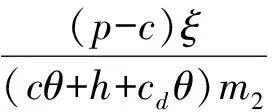


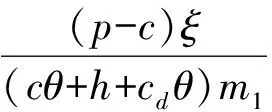





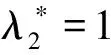
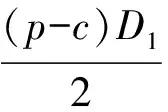

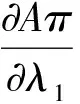

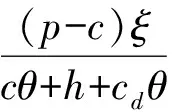
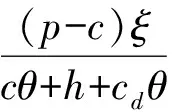
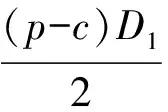
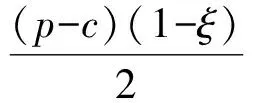
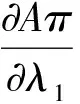

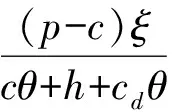

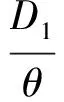
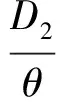


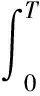


3 算例分析



4 结论

