商用车主动空气座椅悬架的建模与仿真研究

潘公宇，刘永田

(江苏大学 汽车与交通学院，江苏 镇江 212013)



商用车主动空气座椅悬架的建模与仿真研究

潘公宇，刘永田

(江苏大学 汽车与交通学院，江苏 镇江 212013)

建立一种将驾驶室考虑在内的七自由度1/2商用车主动空气座椅悬架模型，采用最优控制理论建立主动控制器，在考虑白噪声路面输入的情况下，运用MATLAB/Simulink模块进行主动空气座椅悬架的性能仿真分析，得到了座椅质心加速度、悬架动挠度等评价指标，分析了时域和频域的响应结果，并且与被动空气座椅悬架进行了比较。结果表明：主动空气座椅悬架能很好的改善汽车座椅的减震性能，提高驾驶员及乘客的乘坐舒适性。

车辆工程；七自由度；主动空气座椅悬架；最优控制

汽车座椅是汽车中将乘客及驾驶员与汽车联系在一起的重要部件，它直接关系到乘员的乘坐舒适性与安全性[1]。主动空气座椅悬架以其优越的减震性能逐渐受到人们的重视，并且引起了众多科研工作者的研究。笔者通过建立一种将驾驶室自由度考虑在内的1/2商用车七自由度座椅悬架系统模型，进行动力学分析，并采用最优控制理论，建立线性二次型最优控制器，对主动空气座椅悬架的性能进行仿真研究，并将仿真结果与被动座椅悬架系统性能进行比较。

主动式空气座椅悬架系统由输入部分、控制模块及输出部分3部分组成。工作过程如下：控制模块通过输入部分得到驾驶室地板信息，经过自身预设控制算法处理，得出并发送操作指令到系统输出部分，此系统中即为充放气电磁阀，实现了系统的主动控制[2]。

1 建立主动空气座椅悬架模型

1.1 系统物理模型的建立

现考虑两个非簧载质量垂向位移、车身质量垂向位移与俯仰角位移、驾驶室垂向与俯仰角位移和座椅垂向位移七个自由度，将驾驶室的俯仰对座椅垂向振动的影响考虑在内，并将其作为一个优化指标之一。七自由度1/2车辆主动空气座椅悬架的模型简化如图1[3]。图中，c为驾驶室质心与车架前连接点距离；d为驾驶室质心与车架后连接点距离；e为驾驶室质心与座椅悬架连接点距离；a为车架质心与前悬架连接点距离；b为车架质心与后悬架连接点距离；f为车架质心与驾驶室后悬架连接点距离；g为车架质心与驾驶室前悬架连接点距离。

座椅悬架设计时，座椅受到的纵向力表达式为：

(1)

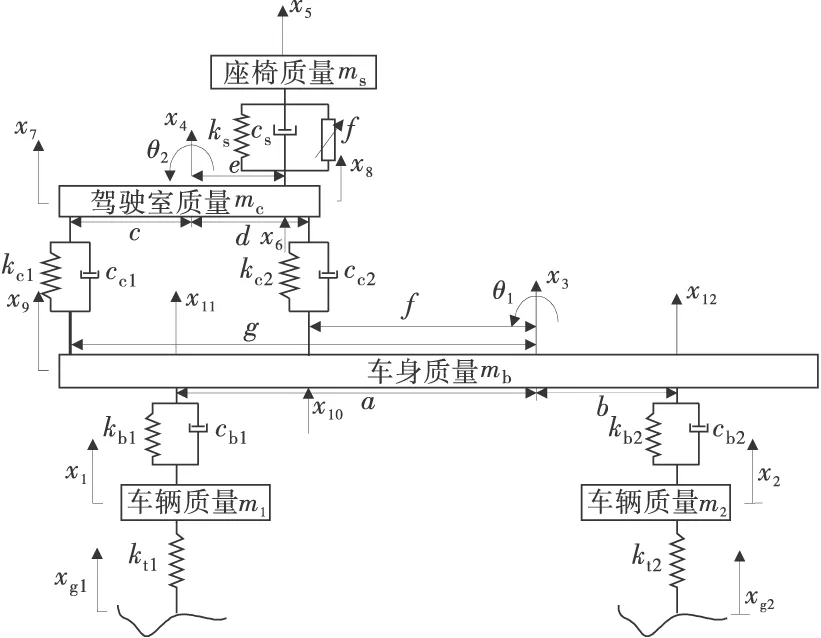
图1 主动空气座椅悬架简化模型

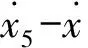
(2)

同时，空气流量q与控制电磁阀电压的关系为：

q=(u-ps)/rp

(3)

式中：vs为气压缸等效容量；as为气压缸有效工作面积；u为控制电磁阀电压；rp为电磁阀阻抗系数。

根据式(2)、式(3)，消去空气流量q，并进行化简，可得式(4)：

(4)

应用拉格朗日方程，得系统运动学5个质量块的加速度方程，驾驶室与车架的俯仰转动方程[4]：

as·ps

在此仅将路面不平度作为输入，并采用滤波白噪声时域表达式将其简化。其方程为：

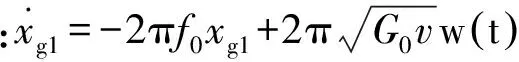
(5)

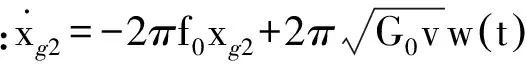
(6)

就七自由度1/2车辆模型而言，前后轮所受路面激励存在如下关系：

(7)

式中：td=(a+b)/v，选取不同的速度情况，其时域仿真如图2。

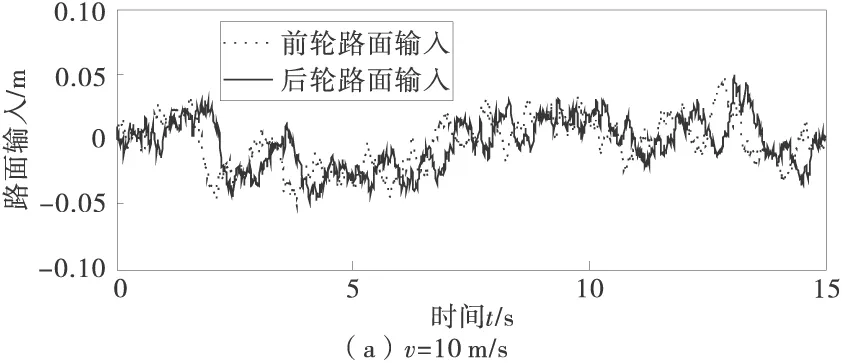
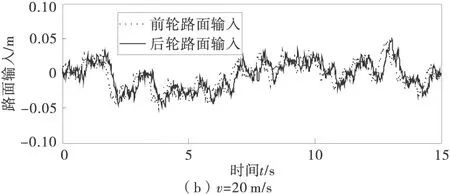
图2 前后轮路面激励输入

将汽车座椅的质心加速度作为重要参考指标，因此选用如下状态变量和输出向量：

可得系统的状态方程：

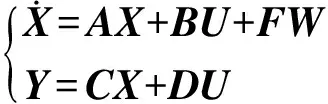
式中：U=(u)为控制输入；W=(w(t))为高斯白噪声输入。

1.2 数学模型的解

通过系统动力学方程可得矩阵的表达式如下：

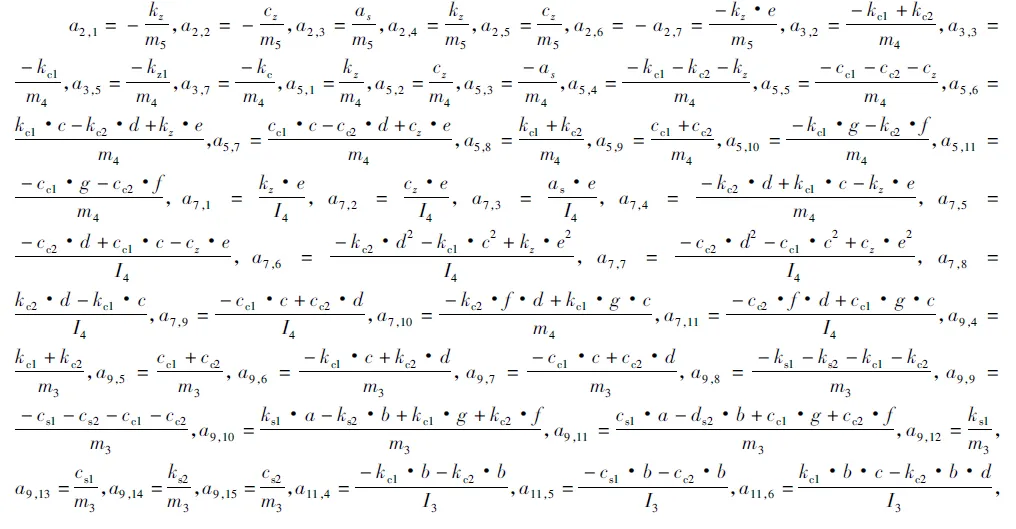
2 设计最优控制器

2.1 最优控制理论阐述

通过建立最优控制器，结合提出的加权系数及控制目标，求解系统状态方程的最优解，本系统的控制目标是使座椅质心加速度尽可能减小，同时限制座椅动挠度及驾驶室俯仰等，并且使消耗的能量较小[5]。优化指标如式(8)：

(8)

式中：q1,q2,q3,r为加权系数。

提出控制向量Y：

(9)

式中：Q为控制矩阵；R为加权矩阵。

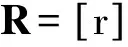
2.2 加权系数及最优解的求取

笔者根据层次分析法[6](AHP)求得各指标加权系数分别为： q1=600 000， q2=5 469， q3=5 176。当加权系数值确定后，经黎卡提方程可求出最优控制反馈矩阵[7]，形式如下：

PA+ATP-(PB+N)R-1(BTP+NT)+Q=0

(10)

最优控制反馈矩阵K=BTP+NT,由加权系数及车辆参数决定。t时刻最优控制量u可根据反馈状态变量X求得：u=-KX。反馈增益矩阵K可通过MATLAB中提供的LQR函数求得：

(K,S,E)=LQR(A,B,Q,R)

(11)

3 在MATLAB中的仿真实现

3.1 仿真条件的设定及模型的搭建

在Simulink中建立模拟仿真模型，得出仿真结果[8]。文中车型相关参数为：

m1=m2=45.5kg,mb=14 380kg,mc=184kg,ms=75kg,kb1=70 000N/m,kb2=100 000N/m,cb1=4 040N·s/m,cb2=8 040N·s/m,cs=455N·s/m,

ks=18 000N/m,e=0.35m,kc1=16 460N/m,kc2=16 460N/m,cc1=cc2=4 040N·s/m,a=2.7m,b=1.35m,f=1.9m,g=3.1m,c=0.8m,d=0.5m,G0=64×10-6m2/m-1。

设行驶路况为B级路面，车速分别设为v1=10m/s，v2=20m/s，路面不平度系数取上述值。Simulink建立主被动空气座椅悬架模型框如图3。

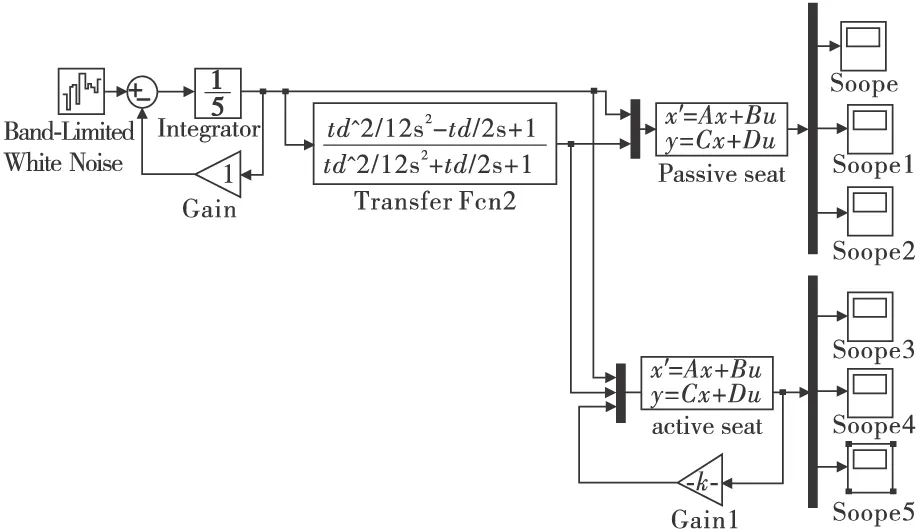
图3 主被动空气座椅悬架系统的Simulink模型

3.2 仿真结果及分析

设置仿真时间t=15 s，考虑不同速度情况下路面输入的影响，并分别从时域及频域角度来分析主被动空气座椅悬架的各性能指标[9]，同时考虑某一速度下各指标的加速度均方根值，从时域图及数值表中直观的分析主动空气座椅悬架的优越性。各仿真结果如图4～图6。

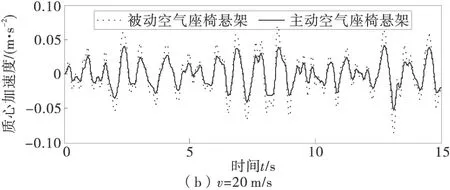
图4 主被动空气座椅悬架座椅质心加速度比较结果

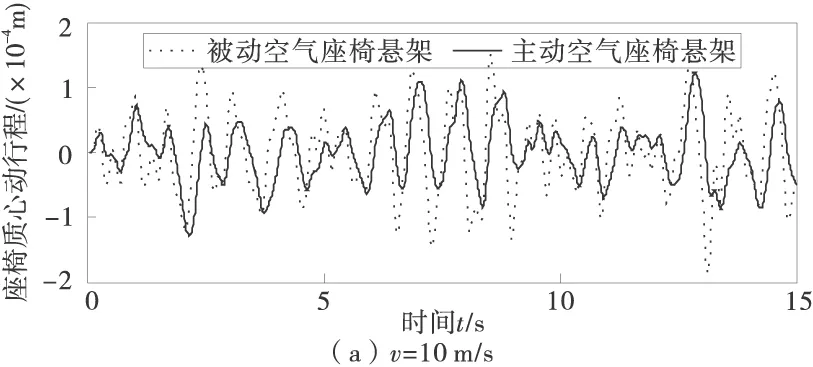
图5 主被动空气座椅悬架座椅动行程比较结果

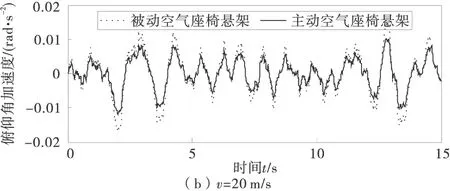
图6 主被动空气座椅悬架驾驶室俯仰角加速度比较结果

表1选取速度v=20 m/s的情况进行分析，选取了主要的空气座椅悬架性能评价指标。由表1可见，座椅质心垂直方向加速度均方根值下降了34.7%，座椅悬架动行程均方根值下降26.7%，驾驶室俯仰角加速度均方根值下降了14.7%。

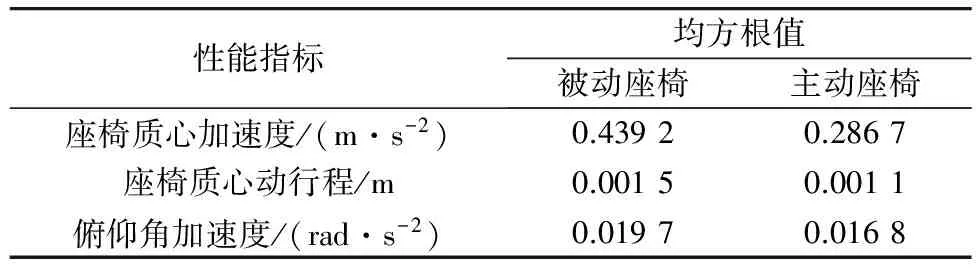
表1 主被动空气座椅悬架性能指标均方根值的对比

在频域分析中，主要关注座椅质心加速度对路面激励速度的幅频响应特性，得到如图7中的曲线。

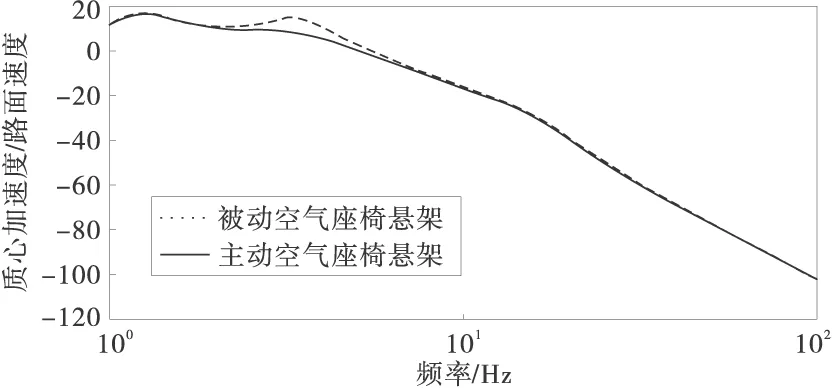
图7 座椅质心加速度对路面激励的幅频响应特性曲线

由图7可见，主动空气座椅悬架在低频区的振峰明显下降，能够有效的衰减座椅质心垂直方向的加速度，在提高车辆乘坐舒适性方面有明显的优势。

4 结 论

1)笔者参考机械座椅悬架，建立采用主动控制器的空气座椅悬物理模型，并将驾驶室自由度考虑在内，得出七自由度1/2车辆座椅悬架动力学方程。

2)为了得出主被动座椅悬架在提高汽车乘坐舒适性的差异，根据系统动力学方程，使用具有最优控制算法的控制器进行主动控制，经过模拟仿真可知：主动空气座椅悬架在提高汽车乘坐舒适性方面有明显优势。

[1] 余志生.汽车理论[M].北京:机械工业出版社,2006:202-205. Yu Zhisheng.Theory of Vehicle[M].Beijing:China Machine Press,2006:202-205.

[2] 潘公宇,任丽萍.空气主动悬架的建模与仿真研究[J].系统仿真学报,2009,21(14):4516-4519. Pan Gongyu,Ren Liping.Research on modeling and simulation of pneumatic active suspension[J].Journal of System Simulation,2009,21(14),4516-4519.

[3] 毛国辉,王小松,郑鸿飞.车-桥耦合振动的联合方程分析方法[J].重庆交通大学学报:自然科学版,2013,32(1):1-4. Mao Guohui,Wang Xiaosong,Zheng Hongfei.Analytical method for joint equation of vehicle-bridge coupling vibration[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(1):1-4.

[4] 靳晓雄,张力军,江浩.汽车振动分析[M].上海:同济大学出版社,2002:212-264. Jin Xiaoxiong,Zhang Lijun,Jiang Hao.Analysis of Vehicle Vibraton[M].Shanghai:Tongji University Press,2002:212-264.

[5] 李传江.最优控制[M].北京:科学出版社,2011:171-243. Li Chuanjiang.Optimal Control Theory[M].Beijing:Science Press,2011:171-243.

[6] 陈士安,邱峰,何仁,等.一种确定车辆悬架LQG控制加权系数的方法[J].振动与冲击,2008,27(2):65-68. Chen Shian,Qiu Feng,He Ren,et al.A method for choosing weights in a suspension LQG control[J].Journal of Vibration and Shock,2008,27(2),65-68.

[7] 黄忠霖.自动控制原理的MATLAB实现[M].北京:国防工业出版社,2007:460-470. Huang Zhonglin.Automatic Control Theory Realization in Matlab[M].Beijing:National Defense Industry Press,2007,460-470.

[8] 赵广元.MATLAB与控制系统仿真实践[M].北京:北京航空航天大学出版社,2009:115-138. Zhao Guangyuan.MATLAB and Practice of Control System Simulation[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2009:115-138.

[9] 张红新,朱思洪.主动座椅悬架电磁作动器仿真研究[J].机械设计,2008,25(4):24-26. Zhang Hongxin,Zhu Sihong.Simulation research on electromagnetic actuator of the initiative seat suspension[J].Journal of Machine Design,2008,25(4),24-26.

Modeling and Simulation of Commercial Vehicle Active Seat Suspension

Pan Gongyu, Liu Yongtian

(School of Automobile & Traffic Engineering, Jiangsu University, Zhenjiang 212013, Jiangsu, China)

A half-car dynamic model was established based on the acquaintance and the analysis of the air suspension, the cab was taken into consideration in this new model. The optimal control method was applied to design the active seat suspension. Two dynamic simulation models of the passive seat suspension and the active seat suspension were set up by MATLAB/Simulink; the random road was taken as the input; the time domain and frequency domain results were compared. The simulation result shows that the active seat suspension can improve the vehicle seat performance and the study has provided the academic reference for the applications of the active seat suspension.

vehicle engineering; 7 freedom; active air suspension; optimal control

10.3969/j.issn.1674-0696.2015.03.31

2013-01-24；

2013-03-16

潘公宇(1965—)，男，江苏丹徒人，教授，博士，主要从事车辆系统动力学、车辆控制技术方面的研究。E-mail：pangongyu@hotmail.com。

U461.4

A

1674-0696(2015)03-157-05