基于多学科多目标遗传算法的摩托车车架优化

莫 明 立

(重庆工商职业学院 汽车工程学院，重庆 400520)



基于多学科多目标遗传算法的摩托车车架优化

莫 明 立

(重庆工商职业学院 汽车工程学院，重庆 400520)

建立摩托车架有限元模型，计算不同工况下的强度、刚度以及自由模态和约束模态，验证了一维管梁单元模型可代替二维壳单元模型进行仿真计算。采用正交实验设计对优化变量进行灵敏度分析和选择。以自由模态和约束模态频率为优化目标，强度、刚度以及轻量化为约束条件，建立多学科多目标遗传算法的振动优化方案，得到车架整体系统的最优解，提高了车架结构振动特性。

车辆工程；摩托车架；多学科多目标；遗传算法；振动优化

0 引 言

随着人们对摩托车轻量化和高速化的需求，摩托车振动的问题日益突出，而摩托车的振动对乘坐舒适性、操纵稳定性以及行驶安全性等都有很大的影响。摩托车的振源主要来自发动机激励和摩托车架之间的共振[1]，发动机引起的振动几乎是不可避免的，而摩托车架作为摩托车的骨架，在设计阶段，如何避免与发动机产生共振是必须考虑的因素。普遍的设计方法是在结构的薄弱构件设置加强板，提高车架固有频率，或者以车架的模态作为特性因子进行优化设计，忽略了车架的强度和刚度。

摩托车车身结构是一个较复杂的工程系统，既是一个涉及了多学科及学科之间的高度关联、相互耦合的过程，也是一个反复迭代、逐渐接近最优解的过程[2]。如果使用传统的单一学科和单目标进行优化则难以实现摩托车结构的整体综合设计。多学科多目标的设计优化考虑了模型系统各个学科间的相互作用和相互耦合，可以更好实现摩托车舒适性、安全性和轻量化。笔者在摩托车振动特性的基础上，结合多目标遗传算法和多学科优化的方法，在车架最大应力、刚度以及质量不超过原设计的条件下，以自由模态和约束模态为优化目标，得出了摩托车振动优化合理又可靠的最优解。

1 有限元建模

在有限元软件中建立4种有限元模型：一维管梁单元强度计算模型、二维壳单元强度计算模型、自由模态和刚度计算模型、约束模态计算模型，依次见图1。在强度计算模型中，前后弹簧均压缩到极限位置，采用刚性单元进行模拟。约束计算模型中，前减震采用两段Bar单元模拟，中间和后减震均采用Bush单元模拟。发动机用集中质心和质量模拟，使用刚性单元连接到车架固定点，焊点采用节点共用模拟，其它采用二维shell单元和三维Tetra4单元。

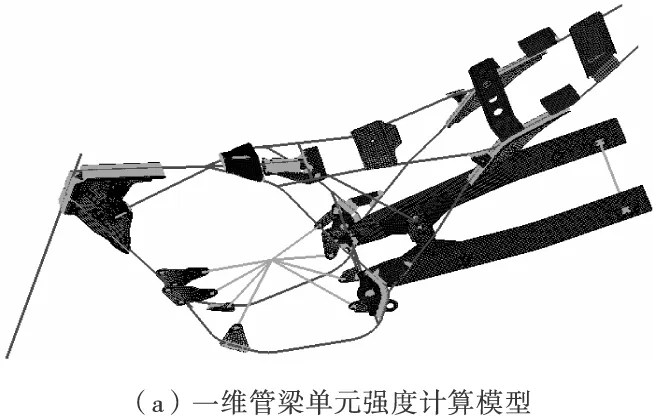
图1 计算模型

2 边界条件及计算

2.1 强度边界条件及计算

根据车架疲劳试验中的加载约束情况，分别计算一维梁单元和二维壳单元在各个工况下的强度。该摩托车架材料为Q235，加载工况的边界条件及梁单元和壳单元模型的最大应力值如表1。

表1 强度边界条件和计算结果

(续表1)

工况边界条件最大应力/MPa梁单元模型壳单元模型垂直加载约束前轮中心y，z向平动，x，z轴转动；后摇臂中心约束所有自由度；后轮轴与后叉两边连接处各施加z正向2150N的力。250．3239．7坐垫加载约束前轮中心y，z向平动，x，z轴转动；后摇臂中心约束所有自由度；副座垫处施加z负向1810N的力。122．2119．1

摩托车架的两种强度计算有限元模型的应力分布位置一致，最大应力值略有差异，梁单元在一定程度上能够真实反映摩托车动态特性，同时节省了大量的计算时间，多学科多目标优化仿真可以使用一维梁单元模型代替二维壳单元模型。

2.2 刚度边界条件及计算

根据摩托车刚度试验及方法建立有限元模型，并施加边界条件，见表2。

表2 刚度边界条件和计算结果

根据摩托车刚度试验要求，选择立管下端节点位移作为约束条件，结果显示：扭转工况下，立管下端在y方向的位移为0.354 mm，弯曲工况下位移为4.371 mm。

2.3 自由模态和约束模态边界条件及计算

自由模态反映摩托车架的结构特性，模拟车架悬挂于无刚度的弹性体上；约束模态模拟摩托车行驶于路面时的车架动态特性，计算时约束摩托车前后轮y，z向的平动自由度，x，z向的转动自由度。计算后模态频率及振型如表3。

表3 自由模态和约束模态

根据该摩托车匹配发动机参数可知，该发动机激励频率主要集中于70～145 Hz之间，根据振型与发动机发生共振的关系可知，1阶自由模态和7阶约束模态频率与发动机发生共振的可能性较小。笔者选2阶自由模态频率和8阶的约束模态频率作为优化目标。

3 优化变量选取及灵敏度分析

根据要求该摩托车架可优化的管件有9组，板件有10组。选取9组管件的外径〔见图1(b)〕和壁厚、10组板件的厚度〔见图1(c)〕作为优化变量，优化变量取值范围见表4。以2阶自由模态和8阶约束模态为优化目标，对选取的优化变量进行灵敏度分析，选取对优化目标影响较大的变量，从而节约优化成本和优化时间。

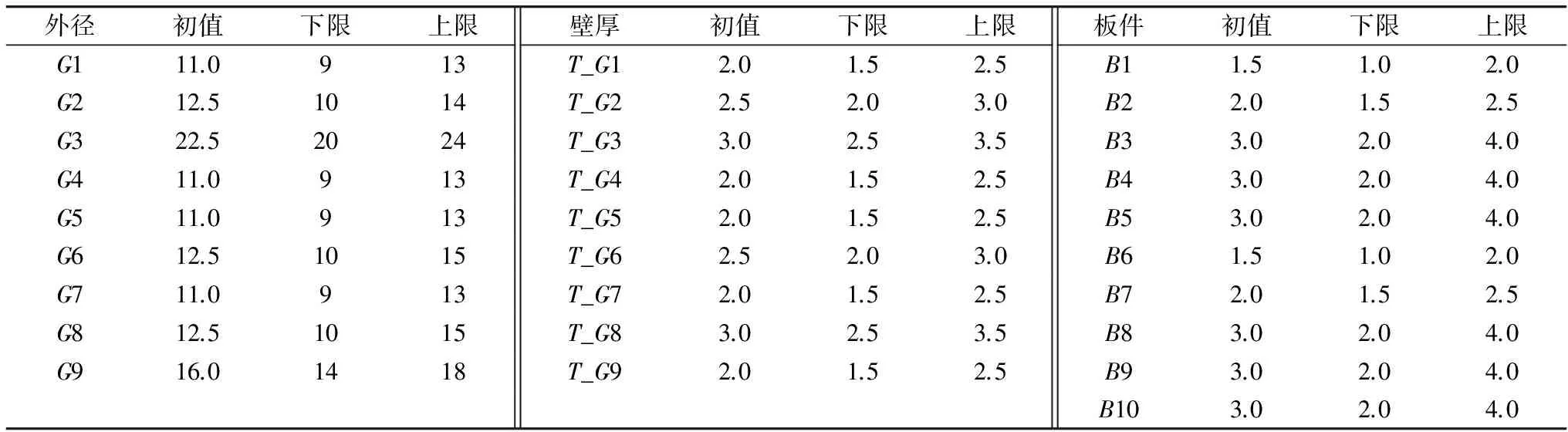
表4 优化变量取值范围

灵敏度分析时选用正交试验设计，该试验方法可在试验次数较少的情况下分析各因素对各个响应的影响程度[3]。

笔者选用2水平28因素64次试验筛选对目标频率影响较大的变量，各变量对目标频率的影响程度如图2。

结合两次灵敏度分析结果(见图2、图3)，将每组变量的灵敏度值进行比较，筛选出管件优化变量为G1，G2，G3，G4，G5，G7，G9，T_G1，T_G2，T_G3，T_G4，T_G5，T_G7，T_G9。板件的优化变量为B2，B3，B5。

图2 自由模态灵敏度分析

变量依次为：B5，B4，B3，B9，B10，B8，B1，B2，B6，B7，G1，G2，G9，G3，G8，G4，G7，G5，G6，T_G1，T_G2，T_G9，T_G3，T_G8，T_G7，T_G5，T_G6，T_G4。

图3 约束模态灵敏度分析

变量依次为：B5，B4，B3，B9，B10，B8，B1，B2，B6，B7，G1，G2，G9，G3，G8，G4，G7，G5，G6，T_G1，T_G2，T_G9，T_G3，T_G8，T_G7，T_G5，T_G6，T_G4。

4 多学科多目标优化

4.1 优化方法介绍

笔者以摩托车架强度、刚度和质量作为约束条件，2阶自由模态和8阶约束模态最大化作为优化目标，采用多学科多目标遗传算法对模型优化[4-5]，得到最优解。采用基于Hyperstudy平台的多目标遗传算法( Multi-objective genetic algorithm )对模型优化, MOGA可提供一系列的帕雷托解 (Pareto-optimal solutions)，而非单一解。Hyperstudy平台的遗传算法约束优化问题采用外点罚函数将约束问题转化为无约束问题。将罚函数定义在可行域外部，这样在计算时只需考虑违反约束的设计[6]。适应度函数定义如下：

+r[ (gj(x)-1)t. 0 ]

优化目标函数记作：

maxf(xi)=f(x1,x2,…,xn)

s.t.gj(x)=0

(j=1,2,…,m；i=1,2,…,n)

式中：f(x)为目标函数；gj(x)为约束函数；m为对应函数个数；x为设计变量；n为设计变量个数。

对于可行解x*∈X,当且仅当不存在其它可行解x′∈X使得f(xi)≥f(x*)fi(x)(i=1 ,2 ,…,n)成立，且至少存在一个i0∈(1,2,…，n)，使严格不等式fi0(x)≥fi0(x*)成立，则x*为多目标问题的一个Pareto最优解。 多目标优化结合多学科优化设计的方法在实现多学科子系统并行设计的同时，获得摩托车架系统整体的最优解[7-8]。

4.2 优化结果分析

将管件最优解与标准管件尺寸对比，选择接近最优解的标准管件，选取优化板件厚度。根据选取管件和板件尺寸建立二维壳单元强度计算模型、自由模态、刚度计算模型以及约束模态计算模型，进行仿真计算,优化前后的结果如表5。

表5 优化前后结果

在摩托车架质量减少约1.16 kg的情况下，强度分析的3种工况在最大应力值上均有不同程度的降低，刚度位移也有所降低。在满足质量、刚度和强度的同时，车架2阶自由模态和8阶约束模态频率分别提高至153.94和139.7 Hz。139.7 Hz对应的发动机转速约为8 382 rpm，在摩托车的实际使用中，发动机很少达到这个转速，因此该优化值在实际使用中基本不会与发动机发生共振。

5 结 语

笔者建立了一维梁单元和二维壳单元模型，通过仿真强度工况，验证了采用一维梁单元模型可以较真实的反映摩托车动态特性，可节省大量计算时间。笔者采用基于多目标遗传算法的多学科优化方法对摩托车架的振动特性进行优化，经过模型再次验证，优化结果较理想，为其它同类产品的优化设计提供一定的参考价值和思路。

[1] 顾瑄.摩托车车架动态特性分析与结构改进优化[D].重庆:重庆大学,2007. Gu Xuan.Analysis of Dynamic Characteristics of Motorcycle Frame and Its Configuration Optimization [D].Chongqing:Chongqing University,2007.

[2] 陈黎卿,何钦章,郑泉,等.基于遗传算法的差速器多目标优化设计[J].机械制造,2007(5):25-27. Chen Liqing,He Qinzhang Zheng Quan,et al.Design of differential optimization based on genetic algorithm [J].Machinery Manufacturin,2007(5):25-27.

[3] 朱茂桃,陈亚洲.基于灵敏度方法的车门模态优化[J].重庆交通大学学报:自然科学版,2014,33(1):139-143. Zhu Maotao,Chen Yazhou .Model optimization of car door based on sensitivity method[J].Journal of Chongqing Jiaotong University:Natural Science,2014,33 (1):139-143.

[4] 洪清泉,赵康,张攀.Optistruct & Hyperstudy 理论基础与工程应用[M].北京:机械工业出版社,2012. Hong Qingquan,Zhao Kang,Zhang Pan.Optistruct & Hyperstudy ,Theoretical Foundation and Engineering Application[M].Beijing:Mechanical Industry Press,2012.

[5] 肖成林,周德义,王志明,等.轿车车门的模态计算和组合式优化分析[J].重庆交通大学学报:自然科学版,2011,30(3):465-468. Xiao Chenglin,Zhou Deyi,Wang Zhiming,et al.Modal calculation and combined optimization of car door[J].Journal of Chongqing Jiaotong University:Natural Sciences,2011,30(3) :465-468.

[6] 王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,47(2):102-108. Wang Ping,Zheng Songlin,Wu Guangqiang.Multidisciplinary design optimization of vehicle body structure based on collaborative optimization and multi-objective genetic algorithm [J].Journal of Mechanical Engineering,2011,47 (2):102-108.

[7] 张义民,贺向东 ,刘巧伶 ,等.非正态分布参数的车辆零件可靠性稳健设计[J].机械工程学报,2005,41(11):102-107. Zhang Yimin,He Xiangdong,Liu Qiaoling,et al.Reliability-based robust design of vehicle components with non-normal distribution parameters[J].Journal of Mechanical Engineering,2005,41(11):102-107.

[8] 张义民.任意分布参数的机械零件的可靠性灵敏度设计[J].机械工程学报,2004,40(8):100-105. Zhang Yimin.Reliability sensitivity design for mechanical elements with arbitrary distribution parameters[J].Journal of Mechanical Engineering,2004,40(8) :100-105.

Motorcycle Frame Optimization Based on Multidisciplinary and Multi-Objective Genetic Algorithm

Mo Mingli

(Department of Automotive Engineering, Chongqing Technology and Business Institute, Chongqing 401520, China)

The finite element model of motorcycle frame was established. And the strength, stiffness, the free modal and the constraint modal were calculated and the results verified that the 1D tube model can be instead of the 2D shell element model for the simulation calculation. Orthogonal experiment was used to analysis the sensitivity of design variables and the best was select. With the frequency of free modal and constraint modal being the objective for optimization, and the strength, stiffness and lightweight being the constraint conditions, multidisciplinary and multi-objective optimization for the vibration was established based on the multi-objective genetic algorithm. The optimal solution was obtained and the vibration characteristics of structure were enhanced.

vehicle engineering; motorcycle frame; multidisciplinary and multi-objective; multi-objective genetic algorithm; vibration optimization

10.3969/j.issn.1674-0696.2015.03.35

2014-03-10；

2014-08-01

莫明立(1973—)，男，四川遂宁人，副教授，主要从事汽车安全与故障诊断方面的研究。E-mail: 150011354@qq.com。

U483

A

1674-0696(2015)03-175-04