整体式车桥有限元分析的位移边界模型研究

邵松标，刚宪约，柴 山，李 双

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)



整体式车桥有限元分析的位移边界模型研究

邵松标，刚宪约，柴 山，李 双

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)

车桥有限元分析的关键在于施加正确的位移边界条件，重点是满足车桥的“简支梁”承载模式和约束边界不应导致局部不合理的高应力区等条件。在分析讨论常见的4种轴头约束法的基础上，提出了辅助支承法和RBE3多点约束法两种位移边界建模方法，可以很好的满足车桥变形和应力分析的精度要求。辅助支承法与车桥试验条件比较接近，而RBE3多点约束法具有对边界网格剖分不敏感的特点。通过一个挂车车轴实例分析，对比研究了各种边界模型对计算结果的影响。

车辆工程；整体式车桥；简支梁承载模式；轴头约束法；辅助支撑法

0 引 言

1)对于车桥刚度试验，按照1倍满载轴荷加载，每米轮距最大变形量不应超过1.5 mm；

2)对于强度试验，按照6倍满载轴荷加载，车桥不应发生弯曲失效；

3)对于疲劳试验，按照0.25～2.5倍满载轴荷脉动加载，车桥垂直弯曲疲劳寿命不应低于8×104次。

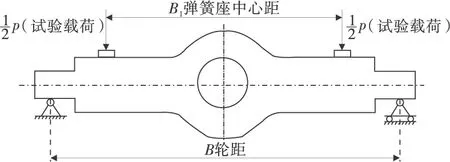
图1 车桥(车轴)弯曲力学性能试验示意

为了提高车桥的力学性能，减少设计-试制-试验成本，在设计阶段利用有限元方法进行结构分析与优化已经成为车桥研发中的重要环节[3]。

陈效华，等[4]通过约束桥壳两端轮毂连接头上所有节点的全部自由度，对车桥进行有限元分析，结果说明该车桥在桥壳局部出现明显应力集中区域，通过改变桥壳局部结构和受力，使得桥壳局部应力明显降低；朱峥涛，等[5]则约束了桥壳两端的纵向和径向的自由度，轴向方向放开，仅取一端的一个点作全约束，通过对3种不同壁厚的桥壳进行计算分析表明，其刚度、强度等满足工程要求。

通过对车桥弯曲力学试验标准和相关车桥CAE分析文献的对比研究，可以得出车桥有限元分析的关键在于正确地施加位移边界条件，重点是满足两个原则：①车桥在加载过程中始终以“简支梁”模式承载；②约束边界不应导致局部不合理的高应力区。

下面以某轮距为1 840 mm的13 000 kg挂车车桥的刚度分析为例，讨论不同边界条件模型对车桥有限元分析结果的影响。按照相关标准要求，该车桥在1倍满载轴荷的作用下，最大弯曲变形不应超过1.5×1840/1000=2.76 mm。

2018年5月28日每个小区于对角线处选择3个点，每个点选择有代表性的0.1 m2，调查有效穗数(剔除5粒以下的小穗)，折算成1 hm2有效穗数；样点内从根部随机取20个麦穗(剔除5粒以下的小穗)，调查穗粒数，计算每穗粒数，千粒质量按该品种常年千粒质量(39.3 g)计算，产量计算公式如下：

为讨论方便，把整车的前后方向称为纵向，车桥轴线方向称为横向，重力方向称为竖直方向。

1 轴头直接约束法

所谓轴头直接约束法，即在安装车轮的轴承位置处，直接将位移约束施加在车桥外圆柱面上。这是目前文献中最常见的一类约束方法，在具体实施上又可以分为4种不同的处理方案：

1)在两端轴承支承的车桥外圆柱面的所有节点上施加纵向和竖直两个方向平动自由度位移约束，并在车桥横向对称截面的某节点上施加横向平动位移约束；或者，在两端轴承支承的车桥外圆柱面的所有节点上施加径向位移约束，并在车桥横向对称截面的最上或最下节点上施加横向和前后两个方向的平动位移约束[6]。两种处理方法得到的结果非常接近。

2)在一端轴承支承的中心位置处，对车桥横截面外圆线上的所有节点施加3个方向平动自由度位移约束；在另一端相同位置处，对车桥横截面外圆线上的所有节点施加对应于整车坐标系的纵向和竖直两个方向的平动自由度位移约束[7]。

3)在一端轴承支承的中心位置处，在车桥外圆柱面的最下端一个节点上施加3个方向平动自由度位移约束；在另一端相同位置处，在车桥外圆柱面的最下端一个节点上施加纵向和竖直两个方向的平动自由度位移约束。

4)在两端轴承支承的中心位置处，对车桥横截面外圆线上的所有节点施加纵向和竖直两个方向平动自由度位移约束，并在车桥横向对称截面的某节点上施加横向平动位移约束；或者，在两端轴承支承的中心位置处，对车桥横截面外圆线上的所有节点施加径向位移约束，并在车桥横向对称截面的最上或最下节点上施加横向和前后两个方向的平动位移约束[8]。两种处理方法可以看作是方案1和方案2改进，二者得到的结果非常接近。

图2分别是4种方案的位移边界施加模型。

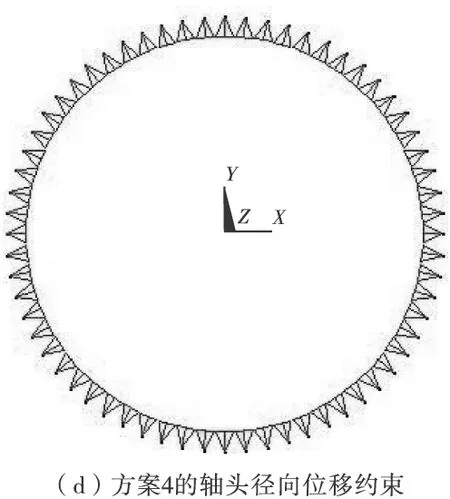
图2 4种方案的位移约束

方案1表面上符合“简支梁”的原则要求。但实际上由于每一端沿车桥方向都存在多个节点同时约束垂直于车桥的平动位移，叠加在一起也就附带着约束了垂直于车桥的两个转动自由度。因此这种方案本质上是严重过约束的，将会使得计算得到的最大弯曲变形远小于实际值，并且过约束将导致在轴承的内侧外置出现不正确的高应力区。

方案2的约束比方案1有所放松，但圆周不同位置处的节点同时约束车桥轴向平动自由度，其叠加效果也是附带约束了垂直于车桥的两个转动自由度，也属于过约束的情况。并且位移约束简化为完全集中于一条外圆线上，会造成该位置处过大的应力结果。

方案3严格满足“简支梁”的原则要求，但该方案也类似于方案2，位移约束完全集中于一点将导致该处变形和应力非常大，不但是该处的应力没有任何实际意义，同时该处不合理的过大转动位移会随之带来其它部位过大的刚性位移，即车桥中部的最大弯曲变形将大大超过实际值。特别是在进行6倍满载轴荷的弹塑性强度分析时，约束节点处不合理的超大的塑性流动导致的转角位移，将使得车桥的变形结果失去意义。

方案4基本满足“简支梁”的原则要求，兼具有方案1、方案2、方案3的优点，端部施加位移约束处的应力虽然也比实际值偏大一些，但相比方案3非常大的应力集中要改善得多。相比较前3个方案而言，方案4应该最接近车桥的实际工作状态。不过，方案4的关键在于每端施加约束的所有节点必须位于同一横截面外圆线上，如果剖分得到节点不能严格满足这一要求，而是存在些许的横向坐标偏差，则方案4在一定程度上也是过约束的，计算得到的车桥变形和应力都会比实际值小些。

图3分别为4种方案的车桥变形图。从图3中可以看出，4种方案的最大弯曲变形(数值位移)差别很大，特别是方案1比方案3、方案4小50%以上，这主要是由于过约束造成的；方案2由于两端约束不对称，导致两端转角变形存在很大差异。

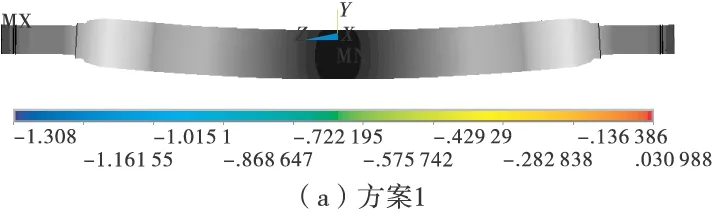
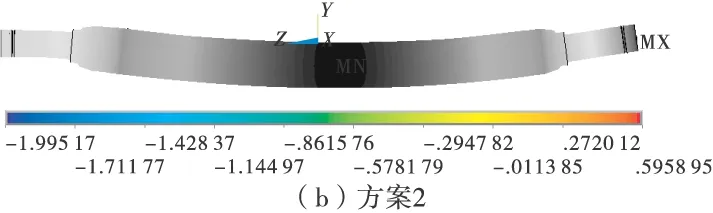
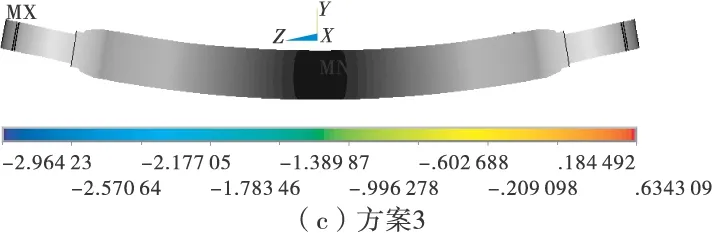
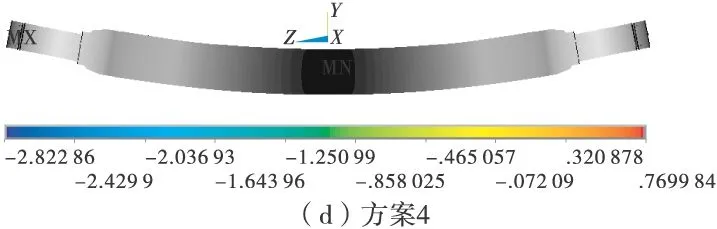
图3 各方案的竖直位移

图4分别为4种方案的车桥Mises应力云图。从图4中可以看出，存在过约束的方案1、方案2在约束边界内侧都存在不同程度的应力集中，并且过约束形成的轴端弯矩支反力大大减小了车桥中间部分的内力，使得中间部分的最大应力只有50 MPa左右，远小于方案3、方案4的120～160 MPa；方案3线性分析的结果在集中点位移约束处的应力远远超过了材料的屈服极限；方案4车桥中间部分的应力分布与方案3基本一致，端部约束处的应力有了明显改善，但约束外圆线外侧的轴承支承部位应力为0，与实际情况略有不符。

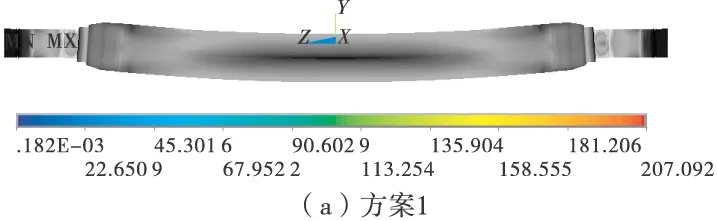
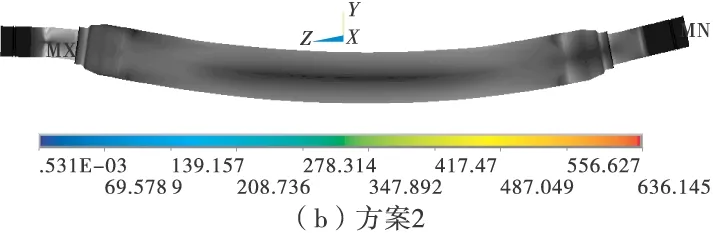
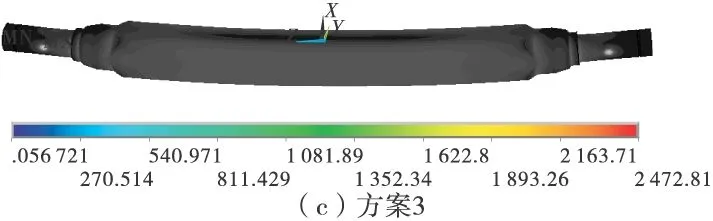
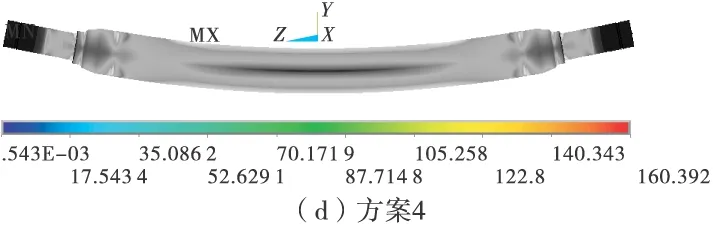
图4 各方案的Mises应力云图

2 辅助支承法

辅助支承法是指在车桥两端的轴承支承部位建立一个简化的辅助支承(如图5)，在支承上施加适当的约束构成简支梁承载模式，辅助支承与车桥之间主要通过径向自由度耦合来进行连接，这种结构形式与车桥、车轴在试验机上的安装形式类似。如图5和图6，在左侧辅助支承的下部对应于原轴承中心的位置的一条纵向线的所有节点上施加3个方向平动位移约束，在另一侧相同位置处的纵向线的所有节点上施加纵向和竖直两个方向的平动位移约束。

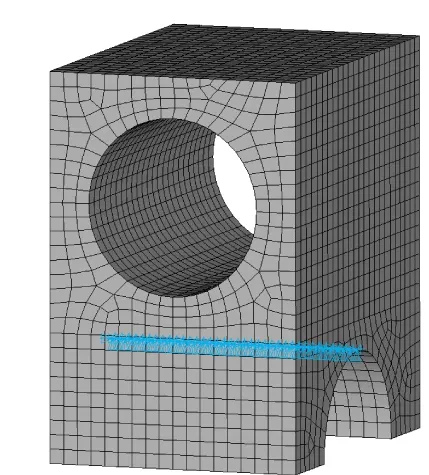
图5 车桥的简化辅助支承

图7为辅助支承法计算得到的车桥的竖直位移和Mises应力图，可以看到结果与轴头直接约束法方案4非常相近，但轴头部分的变形和应力更符合实际情况。

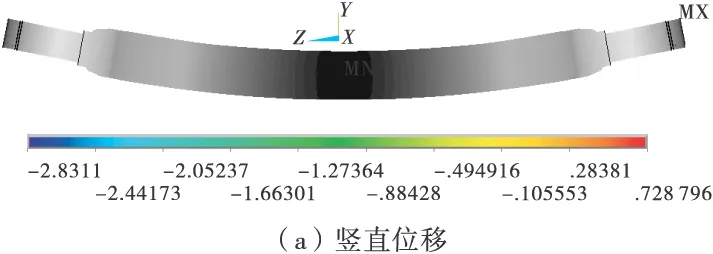
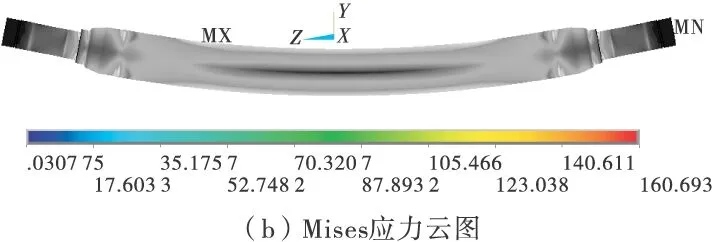
图7 辅助支承法的车桥竖直位移和Mises应力云图

3 RBE3多点约束法

RBE3多点约束法是指在两端轴承支承的中心部位的圆心处建立一个主节点，将轴承支承的车桥外圆面的所有节点定义为从节点集，用RBE3(多点约束)方法将主节点和从节点的3个方向平动自由度连接起来，如图8。然后，在一端的RBE3主节点上施加3个方向平动位移约束，在另一端RBE3主节点上施加纵向和竖直两个方向平动位移约束；为消除车桥刚体自由度，还应在车桥横向对称截面的最上或最下节点上施加纵向平动位移约束，如图8和图9。

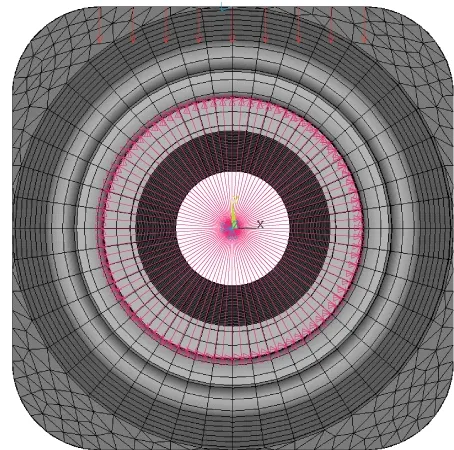
图8 轴承支承处的RBE3多点约束

图10为RBE3多点约束法的车桥竖直位移和Mises应力图，可以看到结果与轴头直接约束法方案4、辅助支承法非常相近，轴头部分的变形和应力也比较符合实际情况。仔细观察还可以发现，轴头直接约束法方案4、辅助支承法和RBE3多点约束法所得轴头竖直向上的最大翘起位移略有差别，这主要是由于施加位移约束的节点的竖直位置不同造成的。

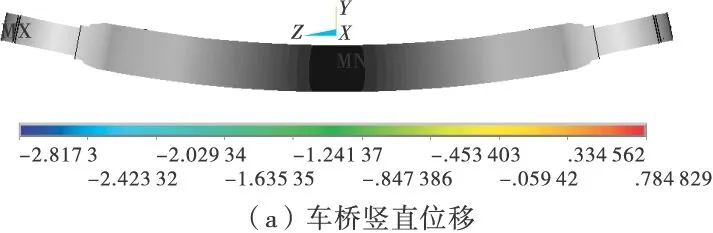
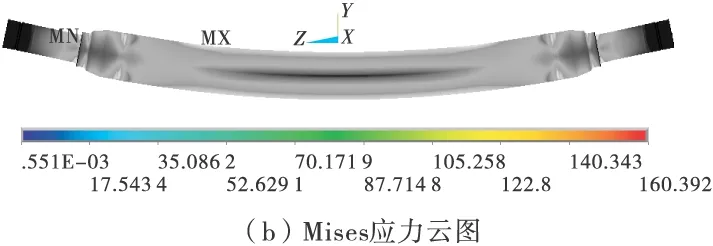
图10 RBE3多点约束法的车桥竖直位移和Mises应力云图

4 结 论

通过对几种边界模型的对比分析，在进行车桥刚度计算时，轴头直接约束法的方案4、辅助支承法和RBE3多点约束法所得位移和应力结果都比较正确，而其他的边界模型方案计算结果均存在较大误差。

1)考虑到自由网格剖分时，轴头直接约束法的方案4每端施加约束的所有节点有时候很难同时位于轴承支承中心处的同一横截面外圆线上，也就会因为过约束导致位移、应力误差，特别是在进行6倍满载轴荷的车桥强度分析时，施加位移约束处的高应力区会提前进入塑性区，增加车桥位移计算误差。

2)辅助支承法适合车桥的刚度、强度、疲劳寿命分析计算，但建模略显复杂，特别是应尽可能保证辅助支承与车桥端部外圆面的节点一致。

3)RBE3多点约束法适合车桥的刚度、强度、疲劳寿命分析计算，并且建模简单，对端部网格也没有特殊要求，应该是车桥有限元分析首选的位移边界模型。

[1] 苏恩生.汽车驱动桥壳的有限元建模与分析[D].长春:吉林大学,2003. Su Ensheng.Finite Element Modeling and Analyzing of Automobile Drive Axle Housing[D].Changchun:Jilin University,2003.

[2] 于东娜,魏建飞,邱阳,等.基于FEM的重型汽车提升桥壳结构强度的分析[J].大连交通大学学报,2011,32(5):24-28. Yu Dongna,Wei Jianfei,Qiu Yang,et al.Finite element analysis structural strength on lifting axle housing of heavy-duty truck[J].Journal of Dalian Jiaotong University,2011,32(5):24-28.

[3] 卢天祥.重型车桥焊接式整体驱动桥壳的有限元分析及优化设计[D].重庆:重庆大学,2007. Lu Tianxiang.Finite Element Analysis and Optimization Design for the Holistic Welding Driving Axle Casing of the Heavy Axle[M].Chongqing:Chongqing University,2007.

[4] 陈效华,刘心文.基于有限元方法的微型汽车驱动桥结构分析[J].中国制造业信息化,2003,32(4):65-67. Chen Xiaohua,Liu Xinwen.The structure analysis of mini bus driving axle with FEM[J].Manufacturing Information Engineering of China,2003,32(4):65-67

[5] 朱峥涛,丁成辉,吴浪,等.江铃汽车驱动桥桥壳有限元分析[J].汽车工程,2007,29(10):896-899. Zhu Zhengtao,Ding Chenghui,Wu Lang,et al.FEM analysis on the drive axle housing of a Jiangling vehicle[J].Automotive Engineering,2007,29(10):896-899.

[6] Topaç M M,Günal H,Kuralay N.Fatigue failure prediction of a rear axle housing prototype by using finite element analysis[J].Engineering Failure Analysis,2009,16(5):1474-1482.

[7] Ghita E,Gillich G R.An analysis about the state of stress in a railway axle[J].Analele Universitǎii Eftimie Murgu Reia.Fascicula de Inginerie,2007 (1):91-96.

[8] 陈喆,王伟.汽车车桥结构有限元分析[J].机械,2012, 39(12):33-37. Chen Zhe,Wang Wei.Finite element analysis of vehicle girder bridge[J].Mechanics,2012,39(12):33-37.

Displacement Boundary Modeling Method for Finite Element Analysis of Rigid Vehicle Axle

Shao Songbiao, Gang Xianyue, Chai Shan, Li Shuang

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, Shandong, China)

Proper boundary condition is the key process of the finite element analysis of axle. The point is to meet conditions that axle bears load in simply-support beam mode and constraint boundary should not lead to impractical local high stress areas. On the basis of the analysis of four common shaft constraint method, auxiliary support method and RBE3 multi-point constraints method were proposed, which can satisfy the accuracy requirements of deformation and stress analysis of axle better. The test conditions of auxiliary support method were very close to axle test, and RBE3 method had the feature of less sensitive to the border mesh. According to analyzing the trailer axle, the influence on calculation results of all boundary models was comparative studied.

vehicle engineering; rigid vehicle axle; simple-support mode; shaft-head constraint method; auxiliary support method

10.3969/j.issn.1674-0696.2015.03.30

2013-10-21；

2013-12-21

山东省自然科学基金项目(ZR2010AL008 )

邵松标(1987—)，男，安徽蚌埠人，硕士，主要从事车辆系统动力学方面的研究.E-mail：shaosongbiao@163.com。

U463.218

A

1674-0696(2015)03-152-05