说题
——一次“寻根之旅”
●凌 红 (湖州中学 浙江湖州 313000)
说题
——一次“寻根之旅”
●凌 红 (湖州中学 浙江湖州 313000)
数学教师的基本功之一就是做题和说题.做题是教师的一种自觉修炼,说题是一种教学提炼.说题概括地讲是教师在精心做题、备题的基础上,阐述对某道习题解答时所采用的思维方式、解题策略及依据,进而总结出经验型解题规律,针对问题的特点寻找它的背景和价值,因此说题也可以成为一种有意义的教学研究活动.笔者曾参加了一次这样的活动,下面谈一谈自己的感受.
例1 设△AnBnCn的3条边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,….若b1>c1,b1+c1=2a1,an+1=an,,则( )
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n-1}为递增数列,{S2n}为递减数列
D.{S2n-1}为递减数列,{S2n}为递增数列
(2013年全国数学高考新课标理科试题)
该题形式新颖,涉及知识点多,入口宽.作为一个选择压轴题,它辩证地体现了计算量与思维量的关系,综合考查了学生运用知识分析问题和解决问题的能力.
1 题意理解
这是一道以三角形的面积为背景的数列问题,是代数和几何问题的交融,因此可以从“形”与“数”这2个方面来分析.
1.1 从“形”的角度
1)三角形列有什么特点?
由an+1=an可知,所有的三角形都有一条等长的边BnCn,可以研究点列{An}的轨迹.
2)如何计算三角形的面积?
由于题意涉及三角形的3条边长,可以直接选择海伦公式(必修5课后习题)计算面积.此时要先计算三角形的半周长
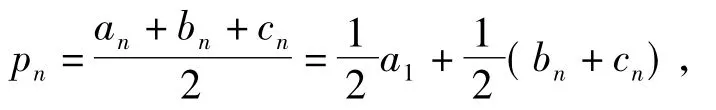
因此可以考察数列{bn+cn}.
1.2 从“数”的角度
利用消元思想,将已知混合递推关系转化为{bn}的递推关系,求出{bn}的通项公式,进而求出{cn}的通项公式.
2)能否较简单地表示出{Sn}的通项公式,进而判断{Sn}的单调性?
由第1)小题可知三角形三边数列的通项公式,可以将面积列{Sn}的通项公式表示出来.
2 解法分析
此题的核心为数列,如何转化为我们熟悉的数列知识来加以解决是问题的关键.
解法1转化为常见数列
1)数列{bn+cn}为常数列.
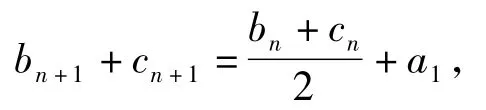
等式2边同时减去2a1,得
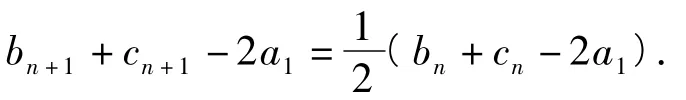
又因为b1+c1-2a1=0,所以{bn+cn-2a1}为零常数列,即bn+cn=2a1.
2)数列{bn-cn}为等比数列.
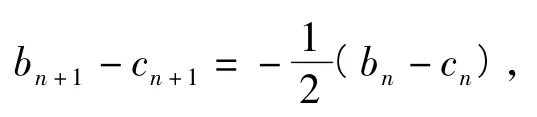
又b1-c1>0,故{bn-cn}是以b1-c1为首项、为公比的等比数列.
3)数列{bn·cn}为递增数列.
4)数列{Sn}为递增数列.
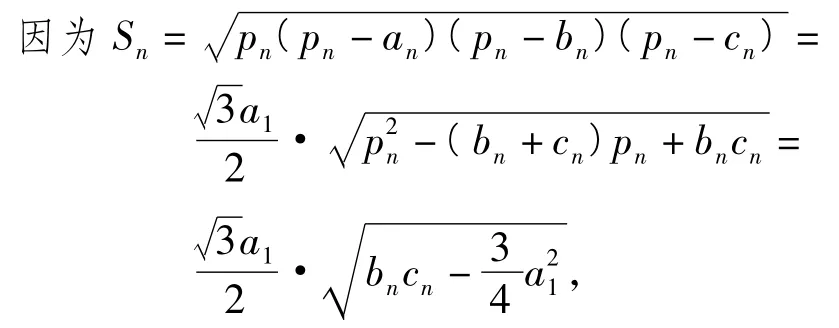
所以数列{Sn}为递增数列.
评注利用方程思想,整体考查了数列{bn+ cn},{bn-cn}的特点,利用恒等变换考查了数列{bn·cn}的单调性.当判断出{bn+cn}为常数列时,发现三角形列的特点:等周长.此时点列{An}在以Bn,Cn为焦点的椭圆上运动,要进一步挖掘点列{An}的运动规律,因此要考查数列{bn-cn}.这一解法根据形与数的结合,相辅相成,层层深入,充分体现了“数形结合百般好”,巧妙地进行了转化与化归,体现了思维的灵活性.
解法2利用好递推数列
1)求数列{bn}和{cn}的通项公式.
①利用待定系数法或不动点法将递推关系


3)判断数列{Sn}的单调性.
考虑数列{Sn}的通项公式对应的函数可知数列{Sn}是单调递增的.
评注利用消元思想,将双数列的混合关系转化为单数列的递推关系,进而求得数列的通项公式.考查了转化与化归思想,以及常见递推关系求通项公式的基本方法:待定系数法.
解法3计算归纳猜想
由选项可知,只需考察数列的前4项即可选出正确答案.
由已知条件,取a1=8,b1=10,c1=6,得.
评注从题型上看,这是一道选择题,考虑能否用排除法.在考试时间十分紧张的情况下,这种小题小做的解题思想不失为一种很好的解题策略,既节省了时间,又保证了答案的正确性,达到了事半功倍的效果.
3 背景研究
数学问题都有它自己特殊的背景,在解决问题的基础上,教师应该探求它的多角度背景,全方位地了解问题,这样才能在教学过程中更好地把握问题的实质,让学生明白数学方法不是“魔术师帽子里的兔子”.有些时候要让学生欣赏到优美的解法,培养兴趣,明白“没有最好,只有更好”的真谛.对于该试题有如下3个方面的背景研究:
3.1 特点探究——中点坐标公式
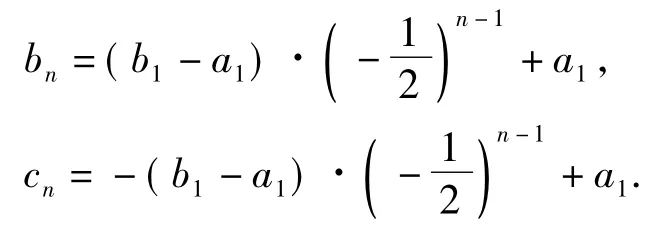
3.2 结构探究——椭圆的焦点三角形
△AnBnCn的周长列是一个常数列,且底边列{an}也是常数列,此时明显地出现了2个定点、1个动点的焦点三角形模型,因此点An在以Bn,Cn为焦点的椭圆上移动.当bn与cn逐渐接近时,点A逐渐接近于短轴端点,此时边BnCn上的高逐渐增大,因此面积列{Sn}是递增数列.
3.3 手段探究——均值代换
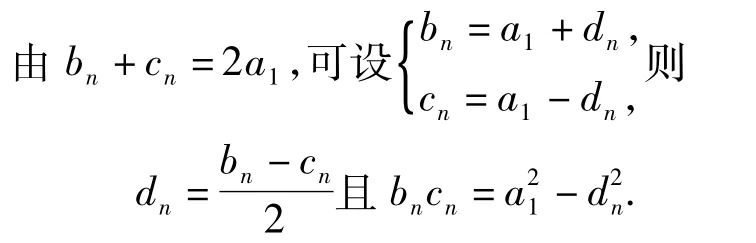
当bn与cn越来越接近时,dn逐渐减小到0,bncn越来越接近.
4 价值研究
该题考查了三角形的面积与周长的关系、等比数列与常数列的概念、数列的递推关系与通项公式、数列的单调性等知识点,检测了学生知识的应用能力和问题转化的意识,是一道难度系数较大的选择题.
通过挖掘其背景,探讨其解法,体会其美妙,使我们对问题有了清晰的认识,并能在不同的场合以不同的方式加以利用,培养学生的数学思维,发挥题目更大的作用.
4.1 例题功能——探究
例1的适当改变,可以在课堂教学中起到很好的教学作用,如以开放题的设问方式,增强问题解决的氛围,提高学生的学习兴趣.
设△AnBnCn的 3条边长分别为 an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,….若 b1>c1,b1+c1=2a1,an+1=an,,试研究数列{Sn}的单调性.
4.2 习题功能——拓展
该试题背景丰富,解题方法多样,在高中学习的各阶段可以拓展学生的思维,如以下例2可作为必修5的模块习题.
例2设△AnBnCn的3条边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,….若b1>c1,b1+c1=2a1,an+1=an,.
1)证明:数列{bn-cn}是等比数列;
2)求数列{bn}的通项公式;
3)判断数列{Sn}的单调性,并说明理由.
4.3 检测功能——能力
例1有一定的难度,作为检测题,可以较好地体现学生的能力,表现出较好的区分度.题目解法较多,也为学生打开思维提供了素材:
1)考查选项的特点,只需列出数列{Sn}的前4项,就可以利用排除法找到唯一的正确答案;
2)例1可以根据庞大的计算过程(通项公式)或敏捷的数学思维(焦点三角形)作出正确选择,因此它可以作为选择压轴题.
5 引申拓展
问题研究后,我们还可以思考问题可能的延伸和拓展,为思维的发散提供途径.
例3设△AnBnCn的3条边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,….若b1>c1,b1+c1=2a1,an+1=an,.记αn=∠BnAnCn,试研究数列{αn}的单调性.
2)根据本题与中点坐标公式的关系,可用定比分点公式进行延伸如下:
例4设△AnBnCn的3条边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,….若b1>c1,b1+c1=2a1,an+1=an,,,试研究数列{Sn}的单调性.
6 结束语
“题目小世界,思维大舞台”.开展说题研究,不仅关系到教师自身素养的提高,也能提高数学课堂的教学效率.让研究试题成为高中数学教师的“自觉”意识,让说题成为高中数学教师交流解题心得的一个重要舞台.
——作业改革探索与实践

