巧用斜坐标系下的直线方程解题

●袁建甫 (余姚市第二中学 浙江余姚 315400)

巧用斜坐标系下的直线方程解题

●袁建甫 (余姚市第二中学 浙江余姚 315400)

平面向量是高中数学的一个重要内容，它丰富了高中数学的知识结构体系，进一步拓展了高中数学问题解决的思维空间.由于其融形、数于一体，具有几何形式和代数形式的“双重身份”，是高中数学知识体系的重要组成部分.而平面向量基本定理是平面向量的一个重要的内容，是应用平面向量知识解决平面几何问题的一个重要而有效的工具.

平面向量基本定理:如果e1，e2是同一平面内2个不共线的向量，那么对于该平面内的任一向量a，有且只有1对实数λ1，λ2，使得a=λ1e1+λ2e2.其中我们把不共线向量e1，e2，叫做表示这一平面内所有向量的一组基底.

这个定理告诉我们:同一平面内，任意一个向量都可以表示为2个不共线向量的线性组合.这样，如果将平面内所有向量的起点放在一起，那么由平面向量基本定理可知，平面内的任意一个点都可以由平面内的1个点及2个不共线的向量来表示.这就类似于平面几何中的“用坐标来表示点”，基底e1，e2的共同起点就相当于平面坐标系中的原点，基底e1，e2就相当于平面坐标系中的x轴和y轴，而实数λ1，λ2的值就相当于坐标系中的横坐标和纵坐标.因此，从本质上讲，基向量法是解析法的一种延伸，而解析法其实就是选择2个特殊的向量(相互垂直的单位向量)作为基向量.

图1

如果一组基底是正交的，(λ，μ)就是向量在直角坐标系下的坐标，如果不是正交基底，我们不妨把它称为在基底下的斜坐标.此时我们也把向量在斜坐标系下的坐标(λ，μ)称为点P的坐标.如图1，不妨称方向的射线为x轴，方向的射线为y轴，夹角为θ，直线OP的斜率为k，倾斜角为α，则可以得到如下几个结论:

结论 1当点 P不在 y轴上时，k=，当点P在y轴上时，θ=α，斜率不存在.

证明P(x，y)为直线OP:y=kx上任意一点，

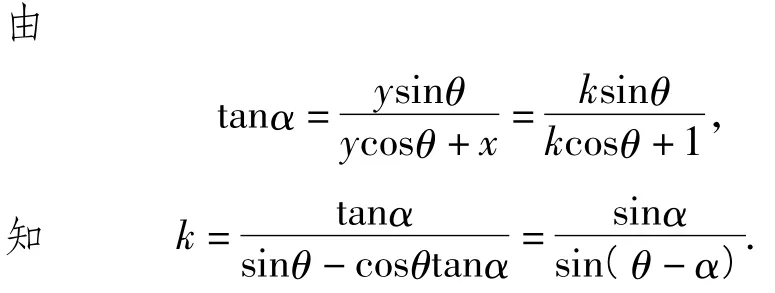
结论2若直线l1，l2的斜率都存在，不妨设为k1，k2，则

1)若直线l1∥l2，则k1=k2;

2)若直线l1⊥l2，则

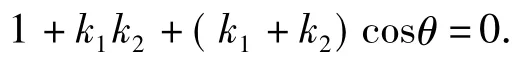
特别地，当l1∥x轴时，l2⊥x轴，此时

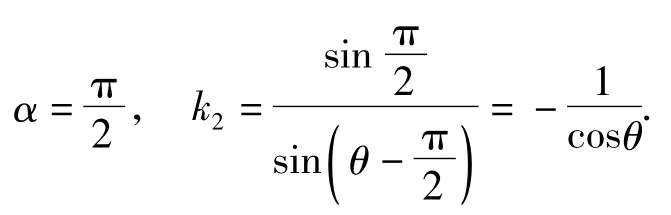
当l1∥y轴时，l2⊥y轴，此时

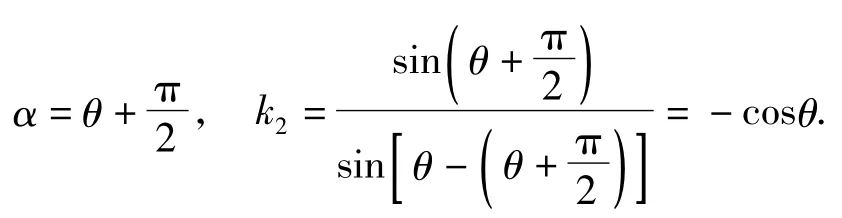
证明1)由l1∥l2得α1=α2，故k1=k2.

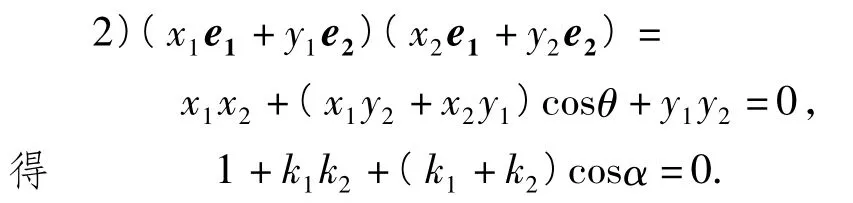
结论3经过点A(x1，y1)，B(x2，y2)的直线方程为

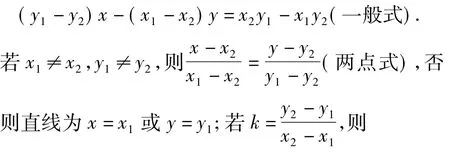
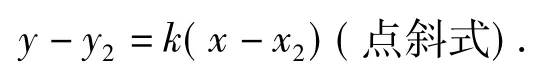
特别地，当A(a，0)，B(0，b)时，直线方程为

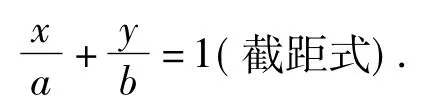
证明不妨设经过点A(x1，y1)，B(x2，y2)的直线l上任意一点P(x，y)，则

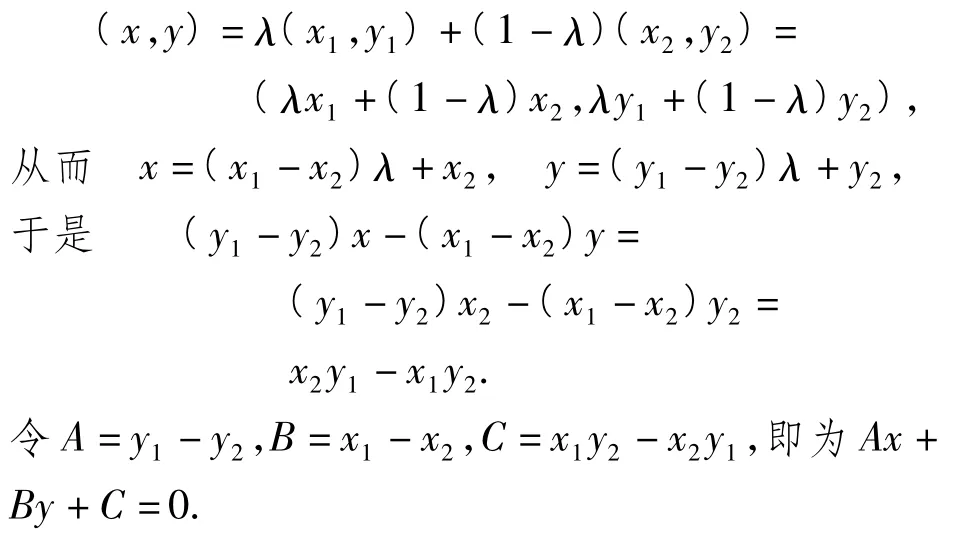
例1已知点O是△ABC的外心，且AB=3，AC=4.若存在非零实数x，y，使得，且x+2y=1，则cos∠BAC =______.

(2014届浙江省宁波市二模试题)

分析如图2，可以把方向上的单位向量看成一组基底，着眼点放在几何图形的特征上.这样方程x+2y=1表示的直线即为中线BD，点O既在中线BD上，又在中垂线上，借此可以联系起来.

解如图2，以方向上的单位向量为一组基底建立斜坐标系xOy，取线段AC中点D，则B(3，0)，C(0，4)，D(0，2)，O(3x，4y).令λ=3x，μ=4y，由x+2y=1，得

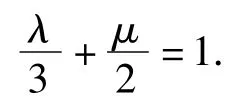
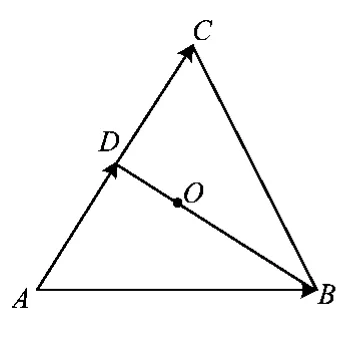
图2

图3

反思本题的关键是特有条件x+2y=1怎么用，从斜坐标系下看它就是一条直线，点O的斜坐标应该与基向量的夹角有关.这里中线BD用到了点斜式方程.

例2在△OAB中，C为 OA上的一点，且，D是BC的中点，过点A的直线l∥OD，P是直线l上的动点，，则λ1－ λ2=______.

(2014届浙江省杭州市二模试题)

分析本题已知，D是BC的中点，联想到点坐标之间的关系;由直线l∥OD，联想到2条直线斜率相等，又直线l过点A，联想到点斜式直线方程;点P满足，可以求出点P的坐标，又P是直线l上的动点，其坐标满足相应的直线方程即可.

解如图3，以方向上的单位向量为一组基底建立斜坐标系xOy，则点A(1，0)，B(0，1)，，从而直线OD的方程为.又AP∥OD，直线AP的方程经过点P，得

反思本题的关键是直线l的方程怎么求，2条直线平行，斜率相等在斜坐标系下仍适用.这里求直线l用到了点斜式方程.

例3如图4，已知点 O是△ABC的外心，AB=4，AC=2，∠BAC=120°.若，则λ1+λ2=______.

(2014届浙江省宁波市一模试题)

分析外心O是3条中垂线的交点，OD⊥x轴，OE⊥y轴，由前面的结论可得直线OD的方程为x+cosθ·y－2=0，直线OE的方程为cosθ·x+ y－1=0，2条直线相交，求出交点即可.

解以方向上的单位向量为一组基底建立斜坐标系xOy，则B(4，0)，C(0，2)，D(2，0)，E(0，1)，O(4λ1，2λ2).又O为△ABC的外心，得OD⊥AB，从而直线OD的方程为.同理可得，直线OE的方程为，2条直线的交点为，故

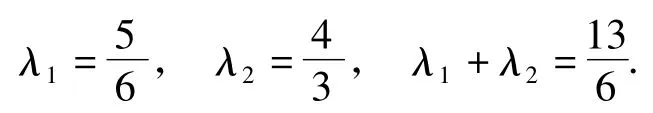
反思这里求直线OD，OE时用到了结论2的2种特殊情况，计算相对比较容易.点O是△ABC的外心，是3条中垂线的交点，可以求出点O的斜坐标，如果是其他的定点呢?能不能用类似的方法来求得斜坐标?下面我们求三角形其他几个“心”的斜坐标.

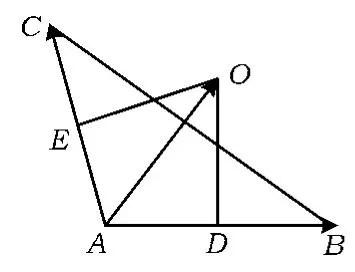
图4

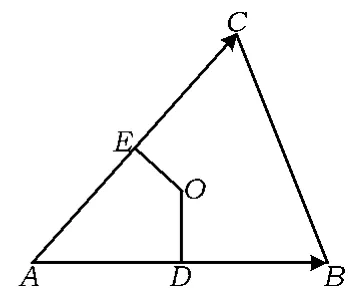
图5

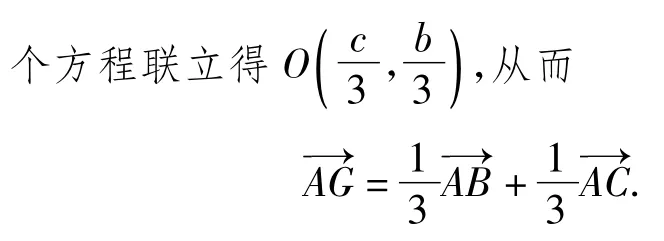
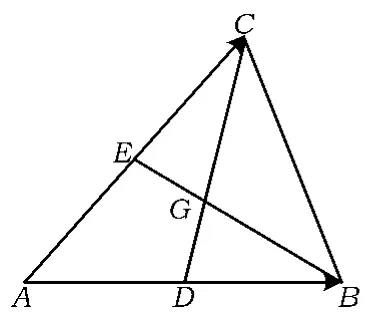
图6

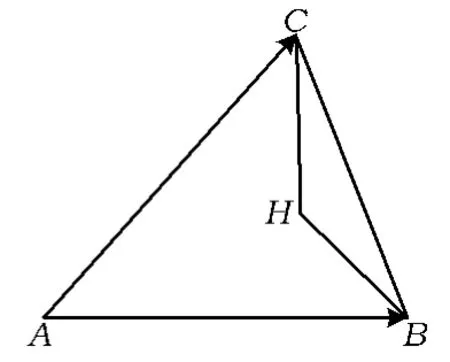
图7

3)如图7，点H是△ABC的垂心，则点H是3条高线的交点.直线CH的方程为x+cosA·(yb)=0，直线BH的方程为cosA·(x－c)+y=0.以上2个方程联立得

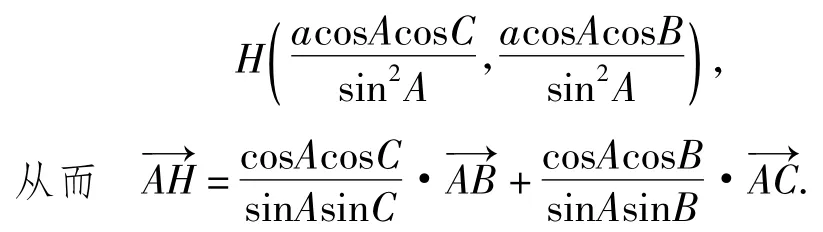
4)如图8，点I是△ABC的内心，则点I是3条角平分线的交点.由角平分线的性质可得

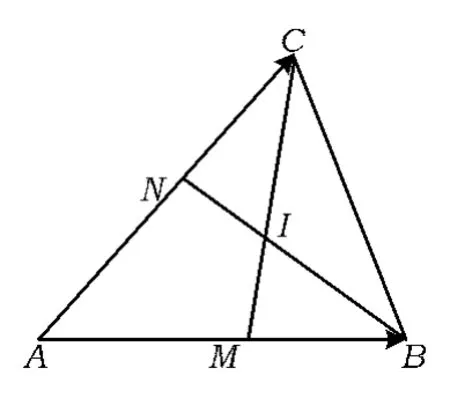
图8

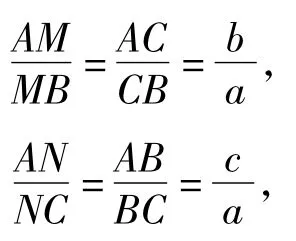
综上所述，构建斜坐标系对解决平行直线、垂直直线、相交直线等问题具有独特的解题功能.坐标化运算直观快捷，学生容易掌握，便于运用“斜坐标系”.构建斜坐标系解题，同时也是培养学生类比推理能力、知识思想方法迁移能力和创新思维能力的良好载体.