一种弹道导弹捷联惯导/地磁组合导航方法

李 镇，王海涌，靳宇航，秦天沐，李晶津，高自谦

（北京航空航天大学 宇航学院，北京 100191）

一种弹道导弹捷联惯导/地磁组合导航方法

李 镇，王海涌，靳宇航，秦天沐，李晶津，高自谦

（北京航空航天大学 宇航学院，北京 100191）

基于惯性器件和磁强计的测量信息，提出一种弹道导弹捷联惯导/地磁组合导航方法。以捷联惯导误差方程为基础建立系统的状态模型，以磁强计测量值与根据地磁场模型计算的地磁场强度值之差作为量测，只用一个观测表达式即同时包含载体的位置及姿态信息。引入状态反馈，利用混合校正的卡尔曼滤波得到系统导航信息的最优估计。仿真结果表明，该算法能有效抑制捷联解算误差的发散，磁强计精度为100 nT时，定位精度2.68 km，姿态精度优于5′。该导航方法完全自主，精度较高，具有一定工程应用价值。

组合导航；捷联惯性导航；地磁场；磁强计；卡尔曼滤波

惯性/星光/GPS三者或两两之间的组合导航是目前组合导航的主要研究范畴[1-3]，但仍存在一定的局限性：虽然星敏感器是目前姿态测量精度最高的姿态确定传感器，但星敏感器体积、重量和功耗较大，价格昂贵，某些型号还难以应用；GPS导航在实战中可能受到干扰，严格地说并不是真正的自主导航。近年来地磁导航研究方向越来越引起业内关注，它具有自主性、无积累误差、成本低、结构简单等优点。因此，某些型号的自主导航，转向惯性和地磁的组合寻求技术解决方案[4-5]。

惯性/地磁组合导航主要有地磁匹配辅助惯性导航和地磁滤波辅助惯性导航两种方式：前者是将地磁匹配定位算法得到的载体位置估计作为量测输入，再利用滤波技术估计惯导系统的误差，该算法须预先存储大量地磁数据，并且累积一段路径才能完成导航，实时性较差；后者直接以磁强计测量值作为量测输入，需要的存储空间较小，同时利用递推滤波技术，实时性较好，卫星和导弹通常采用后者[6]，因此本文的研究主要针对地磁滤波辅助惯性导航。地磁滤波辅助惯性导航的基本方法是将惯导解算位置在地磁基准图上读取的地磁场强度与磁强计测量值之差作为量测，推导并建立观测模型[7-8]，然而该量测仅与载体的位置误差直接相关，姿态信息只能通过滤波技术间接获得。文献[9]利用加速度计敏感重力场，结合磁强计测量值得到载体的三轴姿态，但该算法局限于载体处于静止或不存在线加速度的情况，并且没有进行位置解算。

基于惯性器件和磁强计的测量信息，本文提出一种弹道导弹捷联惯性/地磁组合导航方法。该方法采用地磁滤波辅助惯性导航的组合方式，利用地磁场信息，以三轴磁强计测量值与地磁场矢量计算值之差作为量测，只用一个观测表达式即同时包含载体的位置及姿态信息，通过混合校正的卡尔曼滤波即可得到系统导航信息的最优估计。

1 地磁场矢量模型

地磁场是一个矢量场，它是位置的函数。如果有精确的地磁场分布模型，那么根据地磁场矢量的测量值，经过一定的滤波技术，就能获得载体的位置信息。国际地磁学与高空大气物理学协会每隔5年公布一次IGRF(International Geomagnetic Reference Field)，它具有较为完善的数学模型[10]。地磁场势函数V表示为

由图1可知，地磁场强度B在东北天地理系f中的矢量Bf与其在地球坐标系e中的矢量Be有如下关系：

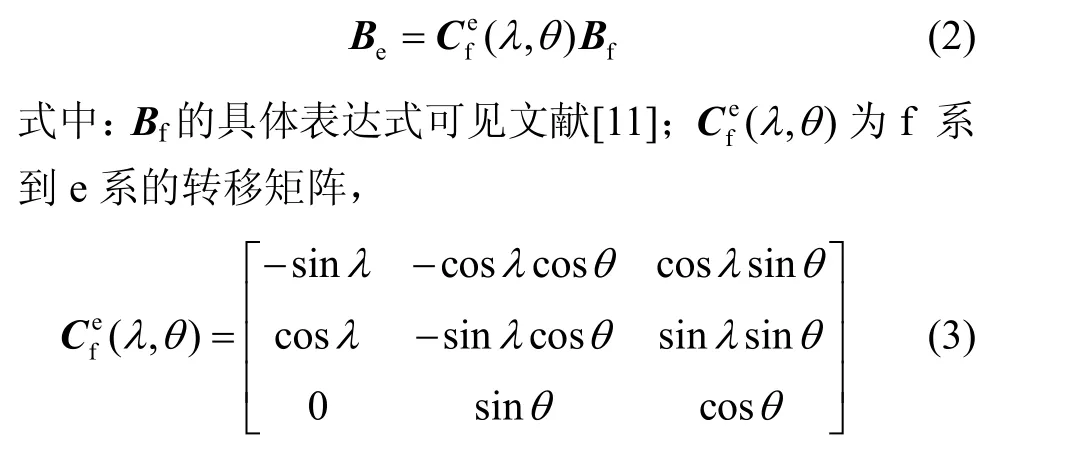
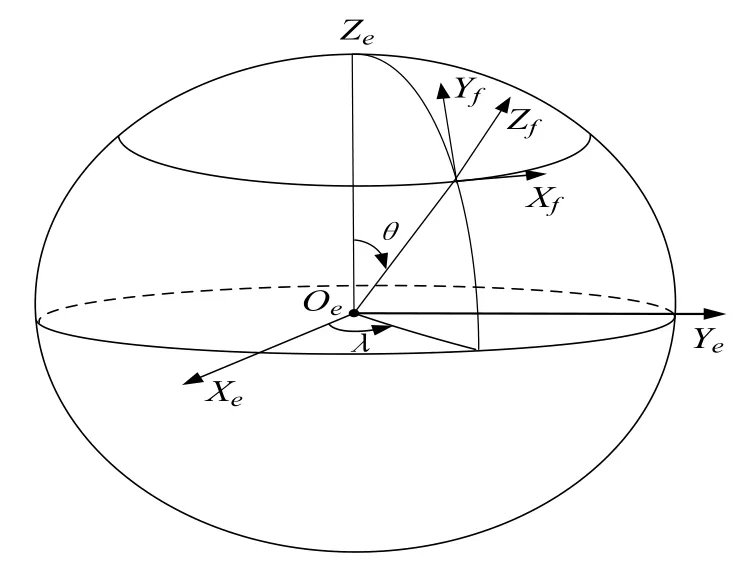
图1 地磁场球坐标示意图Fig.1 Magnetic spherical coordinates

2 捷联惯性/地磁组合系统模型

本文以弹道导弹常用的发射点惯性系li系为导航坐标系，建立捷联惯性/地磁组合导航系统的状态方程和量测方程。

2.1 组合导航系统状态方程

① 数学平台失准角误差方程

忽略陀螺仪的一次项和二次项误差，数学平台失准角误差方程为

② 加速度误差方程

忽略加速度计一次项和二次项误差，加速度误差方程为

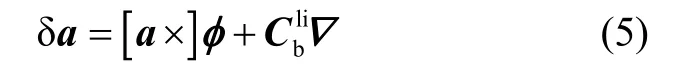
式中：δa为加速度误差，[a×]为加速度计敏感的比力组成的反对称矩阵；▽为载体坐标系b系下加速度计的等效偏置。

③ 速度位置误差方程

在发射点惯性坐标系中，简化引力场模型为球形有心力场，弹道导弹速度位置误差方程为

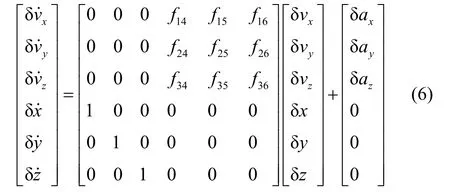
④ 状态方程

综合数学平台失准角、加速度误差、速度误差和位置误差方程，可得如下系统状态方程：

式中：状态向量X(t)各分量分别为3个数学平台失准角、速度误差、位置误差、陀螺常值漂移和加速度计常值偏置；F(t)为状态转移矩阵，

2.2 量测方程

2.2.1 姿态误差角与平台失准角的关系

在捷联惯导系统中，载体姿态角是通过姿态矩阵(“数学平台”)计算出来的。理想情况下，导航计算机计算的导航坐标系应和理想的导航坐标系（li系）一致。然而，由于系统存在测量误差、计算误差和干扰误差等情况，计算的导航系与理想的导航系之间将产生偏差，对应的误差角为平台失准角，用角矢量表示。忽略二阶小量，li系与系之间满足如下关系：

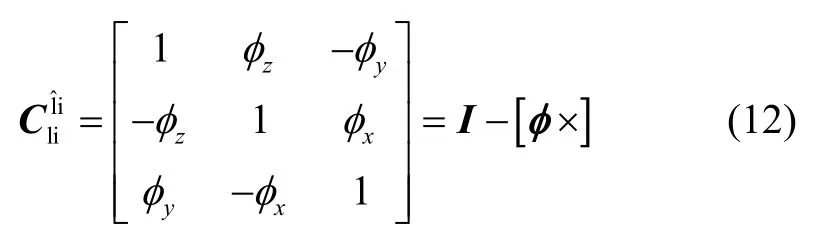
式中，[φ ×]为平台失准角φ的元素组成的反对称矩阵。定义姿态误差角矢量η为

由姿态误差角的定义可知：

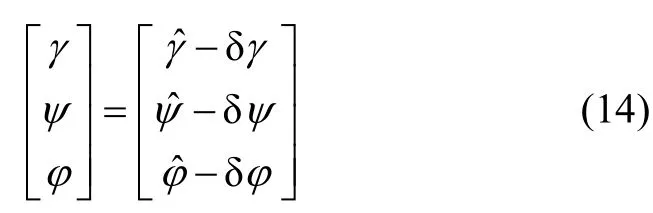
式中，M为误差角转换矩阵，

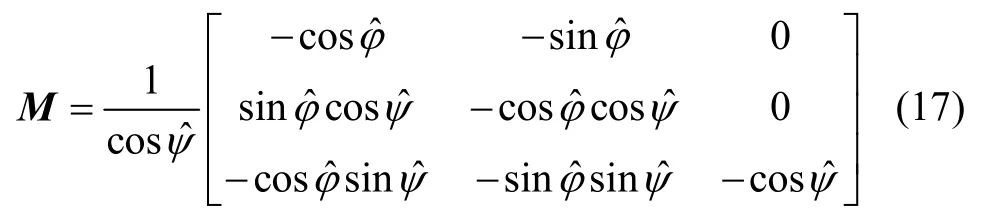
2.2.2 观测模型

三轴磁强计测量值Bm可表示为

根据微分运算法则：

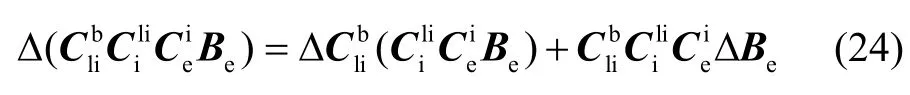
由式(24)可知，磁强计测量误差主要由两部分组成。右边第一项是由于姿态误差产生的测量误差，第二项是由于位置误差产生的测量误差。由于量测Z同时包含了姿态和位置信息，因此可以同时进行定姿和定位。式(24)右边第一项可以简写为

值得注意的是，由于组合系统状态变量中代表姿态信息的是平台失准角φ，而式(35)中的量测是用姿态误差角η表示的，2.2.1节已对他们之间的关系进行了推导，这里只须将式(16)代入，得：

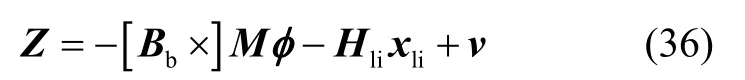
因此，最终的量测方程为

量测矩阵H：

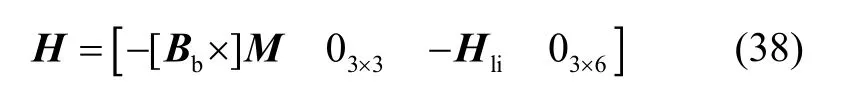
2.3 信息融合

卡尔曼滤波是一种线性最小方差估计。对卡尔曼滤波器估计的利用主要有输出校正，反馈校正和混合校正三种方式，混合校正是前两种校正方式的结合，在不增加计算量的同时，性能优于单独的输出校正和反馈校正。图2为组合导航系统混合校正原理图。

图2 组合导航系统原理图Fig.2 Principle figure of integrated navigation system

3 仿真分析

3.1 仿真条件

① 飞行器发射点北纬39.98°，东经116.34°，垂直向东发射；落点北纬31.59°，东经161.40°；主动段飞行时间160 s，全程飞行时间1100 s，射高761 km，射程4125 km。

② 初始航向角0°，俯仰角90°，滚转角0°；俯仰角误差3′，偏航角误差6′，横滚角误差3′；

③ 采样周期：陀螺及加速度计为0.01 s，磁强计为0.1 s，卡尔曼滤波周期0.1 s；

④ 惯性元件参数：陀螺常值漂移为0.003 (°)/s，陀螺测量白噪声标准差为0.0003 (°)/s；加速度计常值偏置为1 mg，加速度计白噪声标准差为0.1 mg；

⑤ 磁强计测量误差100 nT。

3.2 仿真结果及分析

图3为弹道导弹在发射点惯性系下的轨迹。捷联解算及组合导航相应的位置误差、速度误差、姿态角误差见图4～图6。经过1100 s的飞行，纯捷联解算的位置、速度和姿态误差均发散，位置误差49.18 km，速度误差54.48 m/s，俯仰角误差3.59°，偏航角误差3.44°，横滚角误差 3.31°。利用磁强计信息进行组合导航后，上述误差的发散均得到有效抑制，位置误差2.68 km，速度误差5.23 m/s，俯仰角误差4.74′，偏航角误差3.90′，横滚角误差3.06′。

算法对陀螺常值漂移的估计见图 7。由于观测值同时包含有姿态和位置信息，因此理论上算法也能对加速度计的常值偏置做出估计。当加速度计常值偏置为0.01g时，仿真结果如图8所示。

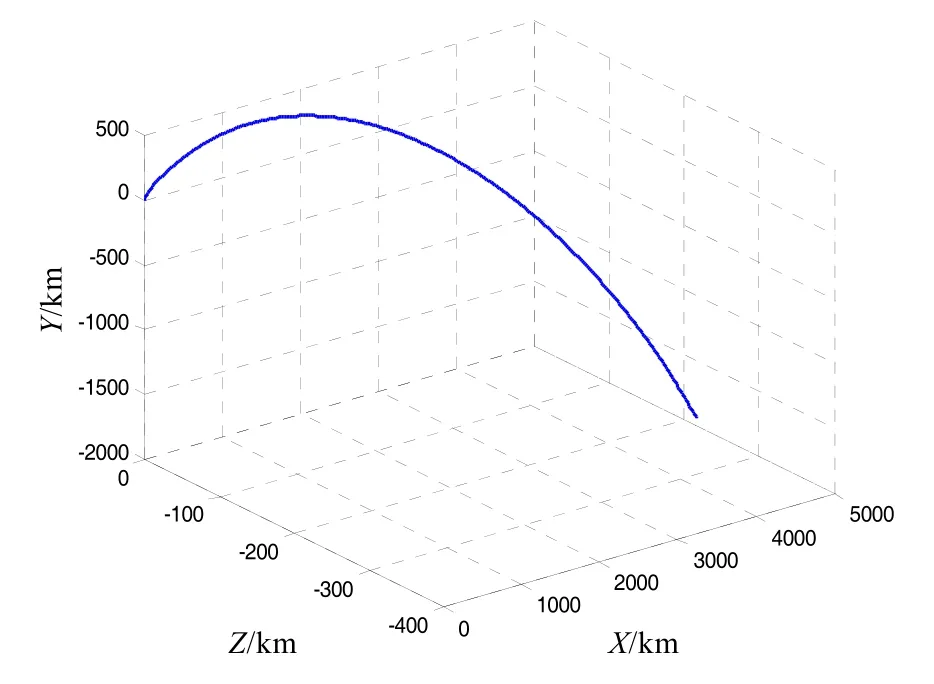
图3 弹道导弹轨迹Fig.3 Trajectory of ballistic missile

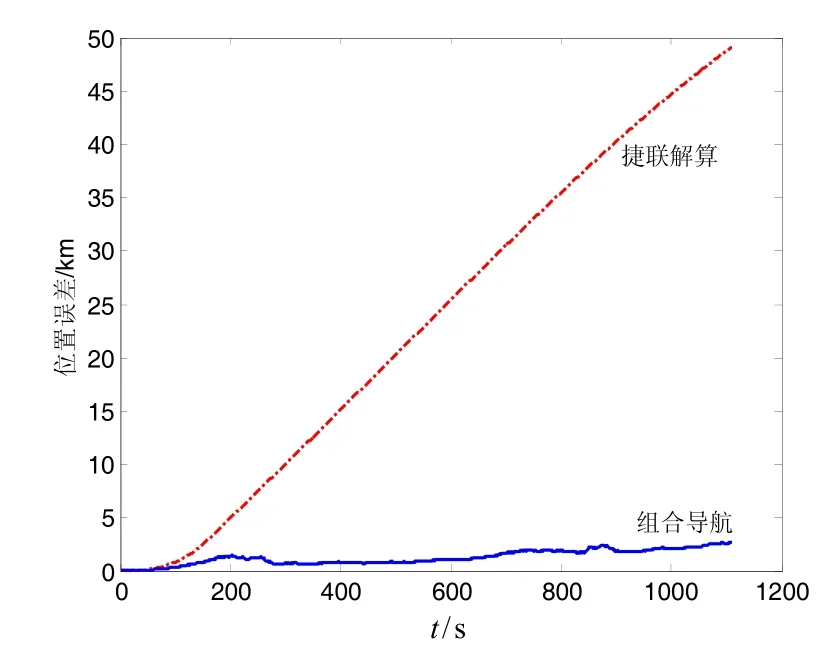
图4 位置误差Fig.4 Position errors

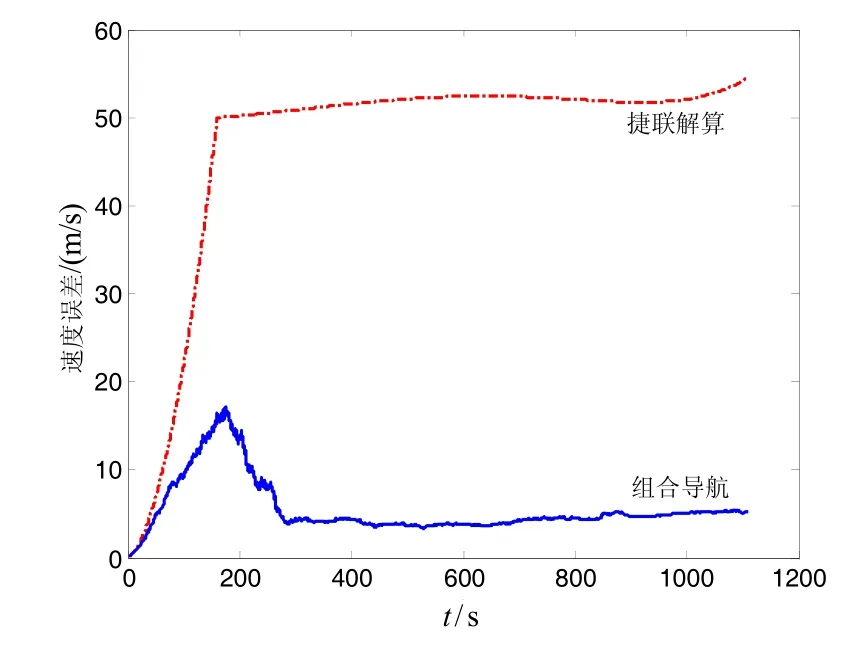
图5 速度误差Fig.5 Velocity errors

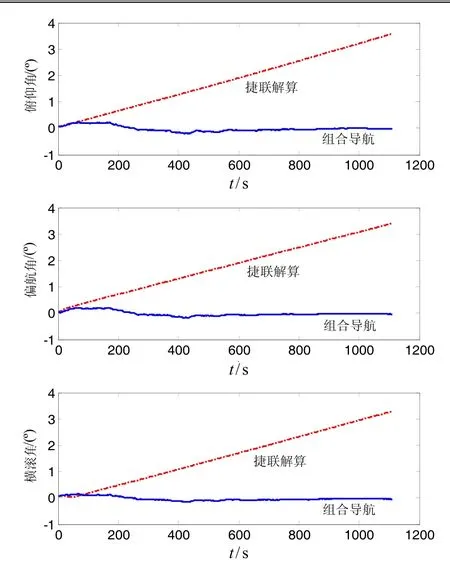
图6 姿态角误差Fig.6 Attitude errors

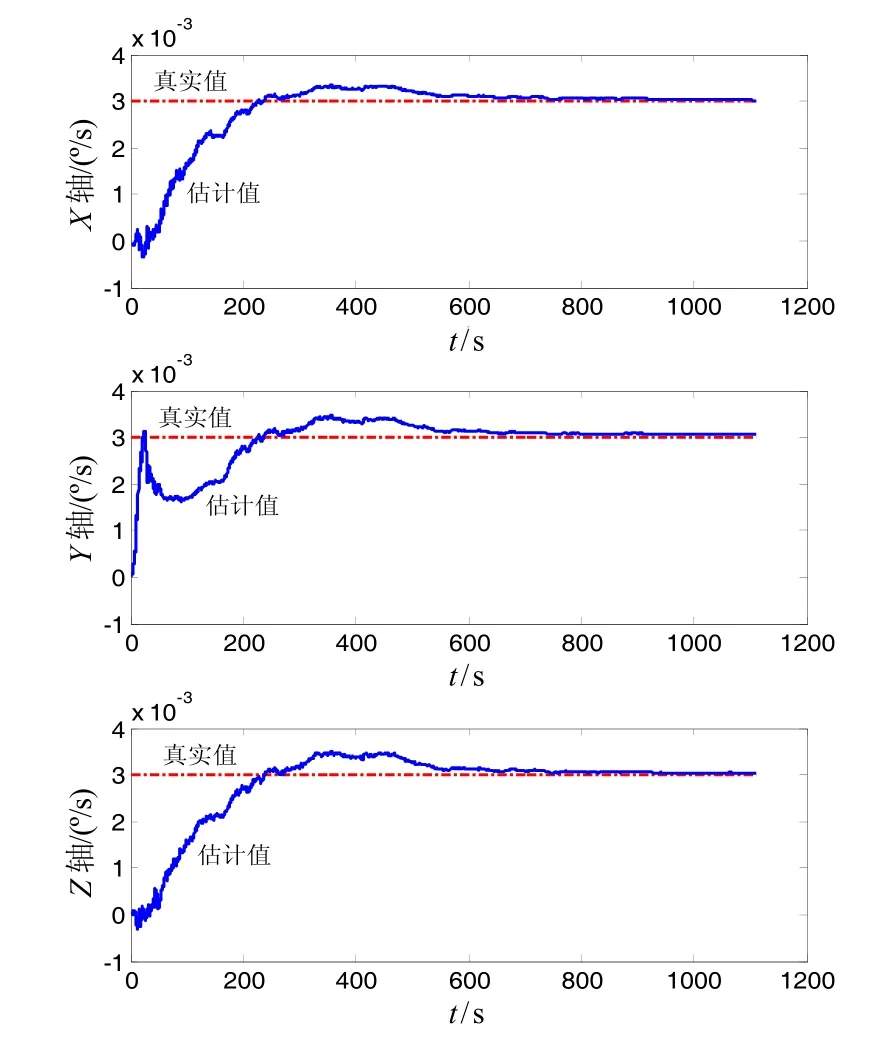
图7 陀螺常值漂移Fig.7 Gyro constant drifts

由图8可知，算法对加速度计在X和Y轴方向的常值偏置估计较好，Z轴方向估计较差，这是由于Z轴方向为与发射面垂直的方向，所受激励较小。需要说明的是，当加速度计精度较高时，导弹的位置及速度误差将主要来源于陀螺漂移引起的姿态解算误差，而算法对陀螺常值漂移的估计将很好的补偿掉这部分误差。

实际发射任务前，应结合异磁场对地磁场模型进行时变修正。为了验证组合导航系统在磁干扰环境中的工作性能，分别选取磁干扰强度为100 nT，300 nT，500 nT，1000 nT，飞行全程的导航参数均方根误差统计见表1。由表1可知，随着磁干扰强度的增加，组合系统的位置、速度和姿态角精度有所降低。当磁干扰强度为1000 nT时，组合系统的定位精度8.78 km，姿态角精度优于40′，与捷联解算的结果相比，仍存在明显的优势。

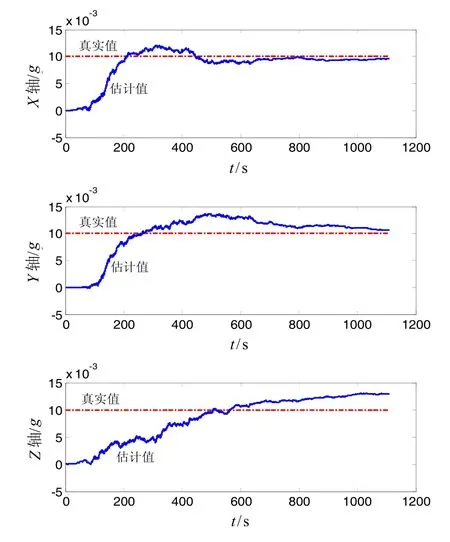
图8 加速度计常值偏置Fig.8 Accelerometer constant biases

表1 不同磁干扰强度对组合系统影响Tab.1 Integrated system influence of different magnetic interferences

4 结 论

基于惯性器件和磁强计的测量信息，提出一种弹道导弹捷联惯性/地磁组合导航方法。以捷联惯导误差方程为基础建立系统的状态模型，以磁强计测量值与根据地磁场模型计算的地磁场强度值之差作为量测，只用一个观测表达式即同时包含载体的位置及姿态信息。引入状态反馈，通过混合校正的卡尔曼滤波进行信息融合，得到系统导航信息的最优估计。仿真结果表明，该算法能有效抑制捷联解算误差的发散，磁强计精度为100 nT时，经过1100 s的飞行，系统的定位精度2.68 km，姿态精度优于5′。需要特别指出的是，当结合异磁场对主磁场模型进行修正时，文中量测模型的推导依然成立。在磁干扰强度为1000 nT时，系统的定位精度8.78 km，姿态精度优于40′。该导航方法完全自主，精度较高，具有一定工程应用价值。

（References）：

[1] 王涛, 王雪梅. 一种新的SINS/GPS组合导航建模与滤波[J]. 弹箭与制导学报, 2012, 32(2): 25-28. Wang Tao, Wang Xue-mei. A new modeling method and filter algorithm of SINS/GPS integrated navigation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(2): 25-28.

[2] 王宏力, 陈聪, 崔祥祥, 等. 适用于弹道导弹的导航星选取方法[J]. 北京航空航天大学学报, 2013, 39(2): 143-147. Wang Hong-li, Chen Cong, Cui Xiang-xiang, et al. Guide star selection method applied to ballistic missile[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 143-147.

[3] Qian Hua-ming, Sun Long, Cai Jia-nan, et al. A novel navigation method used in a ballistic missile[J]. Measurement Science and Technology, 2013, 24(10): 105011.

[4] 朱占龙, 单友东, 杨翼, 等. 基于信息正交性自适应滤波的惯性/地磁组合导航方法[J]. 中国惯性技术学报, 2015, 23(1): 66-70. Zhu Zhan-long, Shan You-dong, Yang Yi, et al. INS/GNS integrated method based on innovation orthogonality adaptive kalman filter[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 66-70.

[5] Guo Cai-fa, Cai Hong, Hu Zheng-dong. Nonlinear filtering techniques for geomagnetic navigation[C]//Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 223(2): 305-320.

[6] 赵国荣, 黄婧丽, 胡正高. 地磁辅助惯性组合导航技术分析[J]. 系统仿真技术, 2013, 9(2): 119-123. Zhao Guo-rong, Huang Jing-li, Hu Zheng-gao. Geomagnetic aided inertial navigation technical analysis[J]. System Simulation Technology, 2013, 9(2): 119-123.

[7] Ma Xiao-jiao, Liu Hong-wei, Xiao Di, et al. Key technologies of geomagnetic aided inertial navigation system[C] //2009 IEEE Intelligent Vehicles Symposium. Xi'an, China, 2009: 464-469.

[8] 刘睿, 董汉成, 王常红. 基于模糊自适应强跟踪滤波的惯性/地磁组合导航方法[J]. 中国惯性技术学报, 2011, 19(3): 329-334. Liu Rui, Dong Han-cheng, Wang Chang-hong. Inertial/ Geomagnetic navigation system based on fuzzy adaptive strong tracking kalman filter[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 329-334.

[9] Zhu Rong, Sun Dong, Zhou Zhao-ying, et al. A linear fusion algorithm for attitude determination using low cost MEMS-based sensors[J]. Measurement, 2007, 40(3): 322-328.

[10] Finlay C C, Maus S, Beggan C D, et al. International geomagnetic reference field: the eleventh generation[J]. International Journal of Geophysical, 2010, 183(3): 1216-1230.

[11] 王仕成, 刘元元, 孙渊, 等. 基于 Legendre 函数的超高阶次地磁场建模方法[J]. 中国惯性技术学报, 2012, 20(3): 333-338. Wang Shi-cheng, Liu Yuan-yuan, Sun Yuan, et al. Method for ultra high-order magnetic model based on Legendre function[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 333-338.

Strapdown inertial/geomagnetic integrated navigation method for ballistic missile

LI Zhen, WANG Hai-yong, JIN Yu-hang, QIN Tian-mu, LI Jing-jin, GAO Zi-qian
(School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China)

Based on the measurement information of inertial instrument and magnetometer, a strapdown inertial navigation/geomagnetic integrated navigation method for ballistic missile was proposed. The state model was established according to the error equations of strapdown inertial navigation system (SINS), and the observation model was constructed by using the difference between magnetometer output and the geomagnetic field intensity calculated by the geomagnetic reference field model, which included carrier position and attitude parameters. With the introduction of state feedback, the optimal estimations of navigation parameters were obtained by the mixedly corrected Kalman filter. Simulation results show that the proposed method can effectively suppress the divergence of the errors. The positioning accuracy is 3.214 km and the attitude accuracy is better than 5 arcmin when the magnetometer’s accuracy is 100 nT. This method has such advantages as fully autonomous navigation and high accuracy that it is suitable for engineering application.

integrated navigation; SINS; geomagnetic field; magnetometer; Kalman filter

V249.3

：A

2015-06-16；

：2015-09-21

航空科学基金（20130151004）

李镇（1988—），男，硕士研究生，从事组合导航研究。E-mail：lizhen@buaa.edu.cn

联 系 人：王海涌（1969—），男，博士，讲师。E-mail：why@buaa.edu.cn

1005-6734(2015)05-0636-06

10.13695/j.cnki.12-1222/o3.2015.05.014