基于经验模态概率分布的光纤陀螺信号处理

崔冰波，陈熙源，龚政仰

（1. 东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 重庆延锋彼欧富维汽车外饰有限公司，重庆 401120）

基于经验模态概率分布的光纤陀螺信号处理

崔冰波1，陈熙源1，龚政仰2

（1. 东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 重庆延锋彼欧富维汽车外饰有限公司，重庆 401120）

为了抑制光纤陀螺随机漂移，基于改进的经验模态分解(EMD)和新型模态筛选标准提出了一种自适应的区间阈值滤波方法。首先分析加入高斯噪声对EMD分解结果的影响，提出有界噪声辅助以改善EMD分解质量，然后针对本征模态函数的概率分布特征提出了基于样本熵的模态筛选标准，最后采用数据驱动的阈值选择方法实现自适应的区间阈值滤波。为了验证算法的有效性，采集一款干涉型光纤陀螺静态漂移信号进行实验分析，结果表明本文方法较基于平稳小波变换和EMD的阈值滤波有更好的去噪效果。仿真分析表明该去噪算法减小了捷联惯性导航系统的航向角误差，均方根误差较平稳小波变换去噪算法改善了约78.6%。

光纤陀螺；经验模态分解；概率密度函数；样本熵

光纤陀螺(FOG)是一种基于Sagnac效应的光学器件，具有易集成、动态范围广以及测量精度高等特点，已成为捷联惯性导航系统(SINS)的理想器件。受信号检测电路中分布电子的影响，FOG测量数据常常包含大量的非线性、非平稳性噪声，由于非旋转所致的非互易性相移非常微弱，使得受载体状态和环境因素影响产生的重复性漂移信号常常淹没在噪声中。对于影响 SINS系统短期精度的随机噪声和随机游走系数，多采用去噪算法直接去除，而长期缓慢漂移误差常淹没在噪声中，需要对其预处理才能软件建模补偿，因此研究适用于非平稳信号的自适应去噪方法具有重要意义。同时，受载体状态和温度环境的影响，准确估计FOG噪声的先验统计信息非常困难[1]，参数化的去噪方法存在收敛速度慢、参数确定繁琐等缺点，因此有必要研究FOG的非参数化去噪方法。

近年来小波分析因其良好的时频特性和多分辨率能力，在非平稳信号的去噪中获得广泛应用，但由于预定义的小波分解参数具有非自适应性，无法保证时变信号小波去噪的效果。经验模态分解(EMD)是一种数据驱动的时域自适应分解算法，能根据信号成分的震荡特性和幅值大小自适应生成有限个物理意义明确的本征模态函数(IMFs)[2]。研究表明，EMD较小波分析方法更适合于处理非线性序列[3]，且基于部分IMFs集合进行信号重构等同于自适应时域滤波[4]。由于缺乏严谨的理论框架，EMD存在许多待解决的问题，其中模态混叠和端点效应最为突出，Wu等人提出的整体经验模态分解(EEMD)显著改善了EMD的实用性[5]，但是噪声的加入使其在低频IMFs中产生了虚假的模态，降低了EMD的数据驱动特性，且显著增加了运算量。文献[6]分析了随机噪声对非线性信号EMD分解的影响，结果表明其主要影响低阶模态的分解精度，因此改善低阶模态的精度可以显著抑制噪声对信号有效成分分解的影响。此外，Kopsinis提出基于模态单元极值大小的区间阈值滤波(EMD-IT)[7]，解决了基于幅值的阈值缩放破坏信号连续性的问题，但其滤波效果受分解精度和模态筛选结果影响较大，且没有建立针对高斯分形噪声的阈值选择规则。文献[8]基于高斯噪声EMD分解的方差传播特性，建立了适用于高斯分形噪声的阈值选择方法，但其同样没有明确提出模态集合的筛选标准。在我们之前的工作中[9-[10]，完成了对EMD分解方法的改进，但没有详细描述其作用机理，受信号信噪比和长度影响较大。

本文针对上述问题，提出了基于有界EEMD (BEEMD)分解和新型模态筛选规则的区间阈值滤波 (BEEMD-IT)，其主要特征包括：① 采用有界的噪声辅助分析(NADA)方法，增强低频模态分解的数据驱动特性；② 针对含高斯噪声信号EMD分解的特性，提出了基于信号模态概率密度函数(PDF)和样本熵(SE)的模态筛选规则；③ 建立了适用于高斯分形噪声的自适应阈值选择策略。实验和仿真结果表明，BEEMD-IT较EMD-IT和基于平稳小波变换(SWT)的阈值滤波有明显优势。

1 EEMD原理

EMD是一种基于信号局部震荡特性的分解方法，信号中的间歇性振荡成分易产生模态混叠现象，同时EMD易受极值点分布影响导致其对异常(如随机噪声)出现位置敏感。为了消除这种由于极值点变动引起的分解不稳定现象，Wu和Huang基于高斯噪声EMD分解后呈出的二进滤波特性[11]和随机共振理论提出了EEMD。设待分析信号为x(t)，白噪声加入的次数为I，噪声的幅值为β，EEMD的实现过程描述如下[5]：

步骤2：对yi(t)分解得到重复步骤1、步骤2共i次，每次均随机生成新的以保证每次分解得到IMFs的统计独立性；

由 EEMD算法描述可知，其分解精度受β大小和 i次数的影响较大，Wu等人建议一般β可取 0.2倍的x(t)的标准差。仿真实验表明，通过增大I可以减弱噪声引入对EMD分解影响，然而这将显著增加算法的运算量。

2 改进的噪声辅助

2.1 噪声辅助特征

Huang认为造成模态混叠的原因是信号中存在间歇性，强化各包络极值点序列的连续性可以改善模态混叠。然而由于模态的过零点对噪声非常敏感，基于有限次噪声辅助实验的样本集合，无法适应于高斯分布的大数定律，即对得到的 IMFs集合求平均无法消除不同噪声辅助产生的差异性。虽然增大实验次数可以降低该误差，但将导致 EEMD整体运算量显著增加。如果仅对噪声主导的模态进行辅助分析，残余噪声存在的模态会在信号重构中直接舍去。此外，EEMD中使用的 NADA存在不同随机高斯白噪声与信号的累加，由于EMD分解对随机噪声非常敏感，可能导致每次分解会生成不同个数的IMFs。实验研究表明，高斯白噪声EMD分解的各阶IMFs能量谱呈现出二进滤波器的特性，IMFs幅值具有稳定的连续性特征，但这种能量传播特性在低频 IMFs中误差较大[5]。由于EMD总是依次筛选出信号中的高频信息，而基于EMD的滤波过程主要是滤除存在于低阶IMFs中的高频噪声，所以如果能正确地选择出含噪声的IMFs，即使是不完全的EMD分解同样能提取出信号的低频特征。

EEMD存在的主要问题包括：① 平均处理的对象是含噪的IMFs，而不是通过加入噪声使过零点改变的包络线均值，这使得有限次平均后的 IMFs中残留较多的噪声；② 由随机共振理论可知[12]，NADA类似于对信号低通滤波，从而能分离出信号中的弱特征信息，其对处理高频成分的模态混叠非常有效，然而受分解时端点效应和非理想包络拟合等因素影响，低频IMFs进行 NADA会生成虚假模态；③ 高斯噪声分解的这种二进滤波特性在低阶 IMFs中误差较大，有限次加噪分解得到的同一阶 IMFs的差异性无法通过平均消除。文献[13]提出一种迭代加噪筛选 IMFs的方法(CEEMDAN)，其筛选出1阶IMFs后停止此次加噪筛选，然后对余项再进行类似处理得到下1阶IMFs。该方法有效地解决了由于 EEMD不同随机噪声辅助分解后IMFs个数不一致问题。由于CEEMDAN基于NADA生成全部 IMFs，其运算量依然较大，且受有限次平均处理的影响，信噪比较高时低频 IMFs中易产生分解误差。

2.2 有界噪声辅助分析

采用EMD和CEEMDAN软件包分析信号y(t)的模态组成，其中EMD算法采用工具箱中的默认设置，CEEMDAN和BEEMD的噪声辅助次数分别为100次和50次，α均为0.2，其中BEEMD仅噪声辅助产生第1阶IMFs，其分解结果如图1所示。

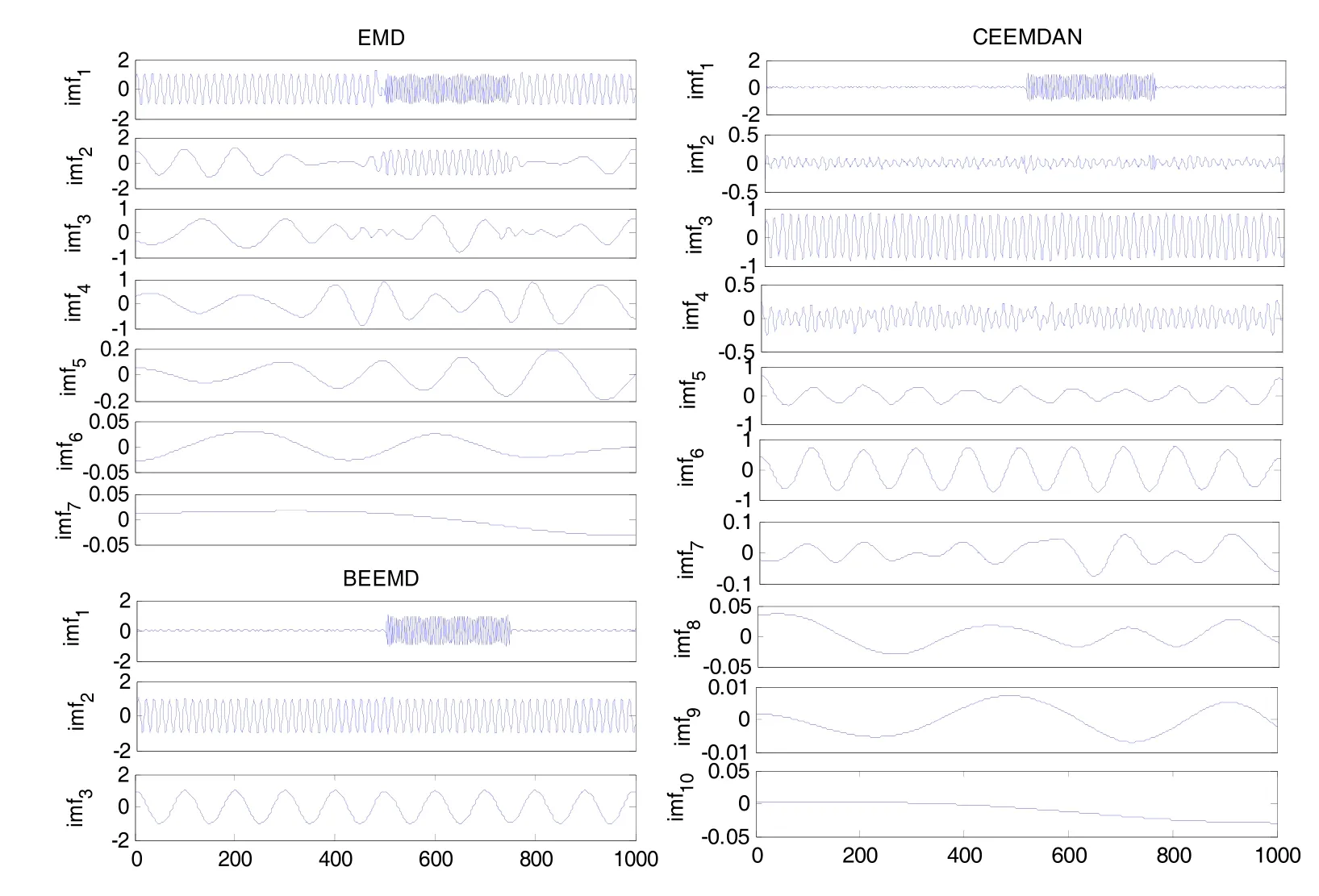
图1 仿真信号经验模态分解Fig.1 Empirical mode decomposition of simulated signal

由图1知，EMD存在明显的模态混叠，无法直接判断出信号中的模态成分。CEEMDAN清晰地分解出了3种频率信号，分别位于第1阶、第3阶以及第6阶，但其产生了大量的虚假模态，混淆了信号成分的物理意义。BEEMD准确地筛选出3个信号分量且没有产生虚假分量，其运算量显著小于CEEMDAN。此外，EEMD、CEEMDAN和BEEMD的NADA引入的残余噪声均方根分别为4.6e-4、2.0e-32和5.5e-33，可以认为迭代加噪筛选方式显著改善了 EEMD算法存在的噪声残留问题。

3 自适应阈值滤波

在基于EMD的阈值滤波中，阈值缩放对象以及阈值的选择显著影响其去噪结果，本文提出了基于PDF和能量估计的方法处理上述问题。基于方差贡献率和相关系数的模态分量筛选受数据长度和信噪比影响较大，建立经验模态分解效果的评价标准是 EMD工程实践中的研究热点。理想情况下，EMD分解得到的各模态都表征独立的物理意义，如果能建立模态的特征函数并以其为标准筛选模态，必然能较好地筛选出具有不同震荡特征的模态。然而由于EMD缺少严谨的理论支撑，直接获取解析形式的模态特征函数非常困难，考虑到概率密度函数(PDF)与特征函数为傅里叶变换对，基于模态的PDF建立模态筛选依据具有可行性。文献[15]提出衡量两PDF几何形状相似性的l2准则，设P和Q分别为PDF序列，定义l2准则为

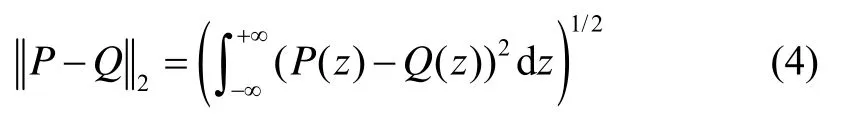
则与式(1)对应的相似度L可定义为

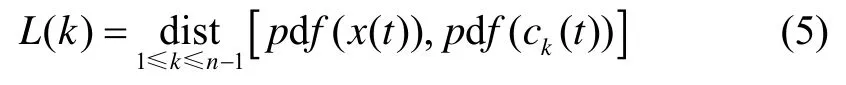
在筛选有效模态时，定义经验公式：

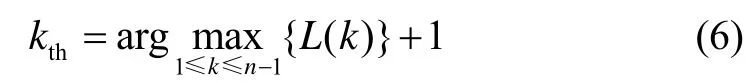
最后，基于kth重构信号就得到了信号中的低频有效信息。文献[8]研究发现，式(6)不适合处理具有长期记忆性特征的陀螺漂移信号，针对不同的Hurst(H)指数的信号需要经验性的修正kth的选取。然而，在含噪信号的分解中，由于l2准则对信号特征分量不加区分处理，并且有效信息筛选容易受特征分量数目影响，导致其信号重构误差较大。

对于含高斯噪声的陀螺信号分解，受高斯噪声分解二进滤波特性的影响，低信噪比模态的分解结果仍近似为规则的高斯分布。为了筛选出有效的模态信息，本文基于样本熵(sample entropy, SE)理论评价模态序列的复杂性，SE（记为Esample）是评价时间序列复杂性的有效工具，值越小说明序列自相似性越高，限于篇幅，样本熵的计算步骤见文献[16]。当模态成分为噪声主导时，其PDF近似为形状规则的高斯分布，即其Esample值较小；随着模态中低频成分的出现，其统计特征发生变化，进而使得其 PDF形状变的不规则，导致Esample值逐渐增大。因此可以基于Esample值的变化确定信号中的低频成分，修改式(6)为

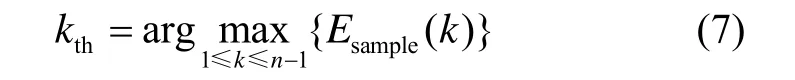
EMD分解结果中必定存在噪声和有效信息共存的模态，即需要采用阈值滤波提取含噪模态中的有效信息。为了建立鲁棒的阈值选择策略，采用周期图法估计陀螺漂移信号的H指数，并建立该H值下高斯噪声EMD分解的方差传播模型。设SH(f)为零均值高斯平稳过程的能量谱密度(PSD)，其表现形式如下[17]：

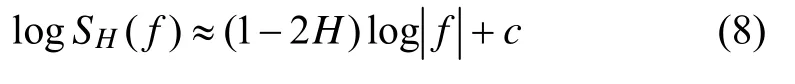
式中，c为常数，通过拟合陀螺输出信号的PSD双对数周期图得1-2H。由于采用NADA改进了EMD算法，其第1阶IMFs为噪声的假设可信度更高。根据EMD分解特点，可以将与第1阶模态具有相近Esample和相似度L的模态定义为噪声主导模态。设m+1为噪声主导模态的边界，则第m阶IMFs的标准差σˆ(m)的鲁棒估计为

4 实验仿真

分别采用BEEMD-IT、EMD-IT以及基于SWT的阈值滤波对FOG输出信号进行去噪处理，其中SWT的分解层数为4，小波基为sym4，采用整体阈值方法，BEEMD-IT、EMD-IT采用相同的阈值策略，三种方法均采用硬阈值滤波。在30℃恒温环境下，采集一款干涉型FOG的静态漂移数据验证BEEMD-T方法的有效性。将FOG安装在静止的温度控制实验箱中，温度传感器安装在陀螺外壳上，调整温控箱温度为30℃。为了消除陀螺启动误差影响，陀螺开机后恒温2 h后采集陀螺数据，采样频率为100 Hz，实验时长4 h。为了方便EMD分析，对FOG数据进行长度为100的平滑，使得数据更新间隔为1 s。BEEMD的加噪次数为50，辅助阶数为1，α=0.2。

图2为30 min陀螺静态漂移数据的特征相关分析归一化计算结果，分别采用l2准则和SE分析BEEMD和EMD分解后的模态。由图2可知，在信噪比较低情况下，l2准则无法分离出漂移信号的趋势项，而采用基于SE的方法仍然可以找到低频特征拐点。信号的前4阶IMFs近似为规则的PDF分布，可将它们定性为噪声主导模态，第5～7阶为噪声混合模态。同时，BEEMD比EMD分解减少2个模态，特征变化尖峰形状更加尖锐，说明其各模态的物理意义较EMD分解结果更加独立。

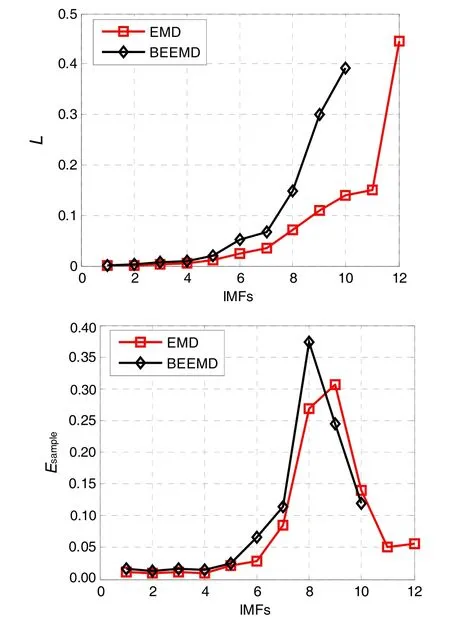
图2 FOG随机漂移信号分析Fig.2 Analysis of FOG random drift signal

对 FOG静态漂移数据双对数周期图采用线性拟合，得其 H值约为 0.74，根据式(8)～(10)可以确定BEEMD-IT阈值，漂移数据去噪结果如图3和表1所示。三种方法对 FOG输出表现为白噪声的量化误差(Q)和随机游走系数(N)具有良好的抑制效果，但是受小波滤波的带通滤波特性制约，SWT无法抑制零偏不稳定性(B)。由于采用改进的噪声辅助分解，BEEMD-IT较EMD-IT在滤除短期噪声上性能更优。SWT和EMD-IT在滤除具有长期记忆性特征的速率随机游走(K)效果不明显，由于 BEEMD-IT的阈值选择考虑到了不同H值数据的特征，其抑制分形噪声效果优于两者。速率斜坡(R)产生原因可能是光源强度的单调变化或者检测电路中受温度影响电子漂移导致的单项缓慢变化，即其是一种确定性单向信号，可以在去噪后建立数学建模进行补偿。

为了直观地对比分析基于BEEMD和SWT的去噪方法对SINS精度的影响，建立战术级陀螺数据的生成模型如下：

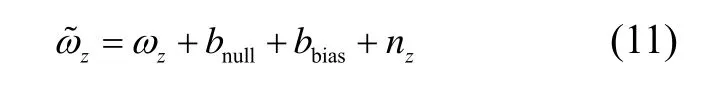
式中：ωz为理论的Z轴向陀螺输出，bnull为3.5 (°)/h陀螺零漂，bbias为一阶高斯马尔科夫模型表示的陀螺偏置，其相关时间为300 s，标准差为0.05°，nz为标准差为0.1°的宽带白噪声。仿真时长为34 m，数据更新率为1 s，轨迹为恒定速度的北向正弦运动，SWT和BEEMD分解参数与FOG数据分析相同。值得注意的是，当信噪比较高时，含周期性角速率信号模态的PDF函数 SE值较小，此时选择PDF的Esample值比第1阶IMFs小的模态作为kth。

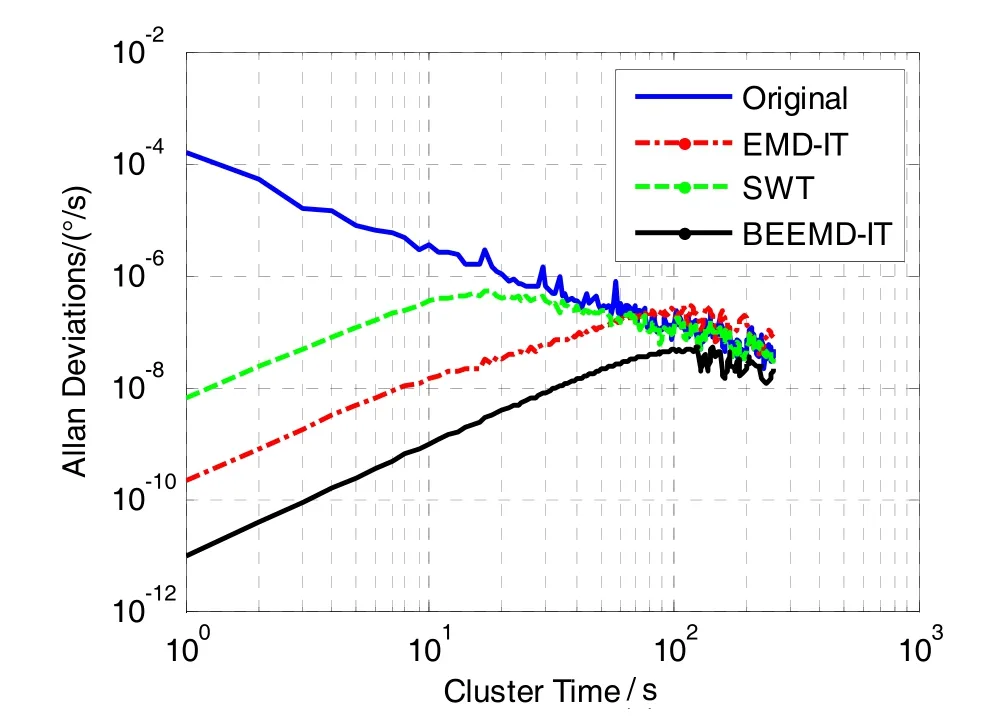
图3 FOG静态漂移信号的Allan方差分析Fig.3 Analysis on Allan deviations of FOG static drift signal

表1 FOG静态漂移信号Allan误差项对比分析Tab.1 Comparison analysis on Allan error terms for FOG static drift signal

图4为基于仿真数据的航向角解算误差，原始数据的航向角均方误差为0.22°，SWT和BEEMD-IT处理后航向角均方误差分别为 0.14° 和 0.03°，且BEEMD-IT较SWT能更好地抑制了长相关周期的噪声对导航解算的影响。可以预见，随着导航系统的运行，两者的性能差别会逐渐增大。

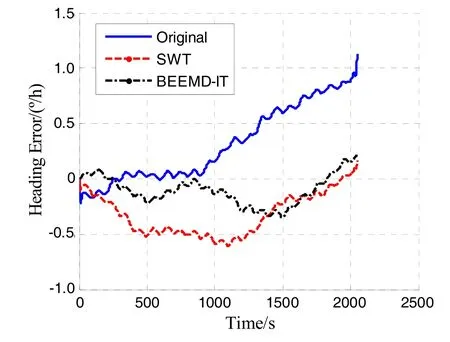
图4 捷联惯性导航系统航向角误差Fig.4 Heading error of strapdown inertial navigation system

5 结 论

综上所述，BEEMD是一种有效的非平稳信号处理方法，它降低了EEMD及CEEMDAN的运算量，增强了EMD低频模态分量的物理意义，减少了虚假模态的生成。基于BEEMD-IT的陀螺信号处理结果表明，基于PDF样本熵的模态评价标准能较好地筛选出复杂微弱信号的有效特征。SINS仿真实验进一步验证了BEEMD-IT处理长相关周期噪声的有效性。然而，受模态均值求解速度的影响，BEEMD当前主要适用于批处理形式的离线信号处理（如光纤陀螺的误差建模、故障诊断等），研究进一步提高其分解速度的方法对其实时在线应用具有重要意义。

（References）:

[1] 李杨, 胡柏青, 覃方君, 等. 光纤陀螺信号的解耦自适应Kalman滤波降噪方法[J]. 中国惯性技术学报, 2014, 22(2): 260-264. Li Yang, Hu Bai-qing, Qin Fang-jun, et al. De-noising method of decoupling adaptive Kalman filter for FOG signal[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 260-264.

[2] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of Royal Society London Series A, 1998, 454: 903-995.

[3] 龚志强, 邹明玮, 高新全, 等. 基于非线性时间序列分析经验模态分解和小波分解异同性的研究[J]. 物理学报, 2005, 54(8): 3947-3957. Gong Zhi-qiang, Zou Ming-wei, Gao Xin-quan, el al. On the difference between empirical mode decomposition and wavelet decomposition in the nonlinear time series [J]. Acta Physical Sinical, 2005, 54(8): 3947-3957.

[4] Flandrin P, GonÇalvès P, Rilling G. Detrending and denoising with empirical mode decompositions[C]// EUSIPCO 2004: 12thEuropean Signal Processing Conference. Wienna, Austria, 2004: 1581-1584.

[5] Wu Zhao-hua, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[6] 杨永锋, 吴亚锋, 任兴民, 等. 随机噪声对经验模态分解非线性信号的影响[J]. 物理学报, 2010, 59(6): 3778-3784. Yang Yong-Feng, Wu Ya-Feng, Ren Xing-Min, et al. The effect of random noise for empirical mode decomposition of nonlinear signals[J]. Acta Physical Sinical, 2010, 59(6): 3778-3784.

[7] Kopsinis Y, McLaughlin S. Development of EMD based denoising methods inspired by wavelet thresholding[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1351-1362.

[8] Yang G L, Liu Y Y, Wang Y Y, Zhu Z L. EMD interval thresholding denoising based on similarity measure to select relevant modes[J]. Signal Processing, 2015, 109: 95-109.

[9] 崔冰波, 陈熙源, 宋锐. EMD阈值滤波在光纤陀螺漂移信号去噪中的应用[J]. 光学学报, 2015, 35(2): 0207001. Cui Bing-bo, Chen Xi-yuan, Song Rui. Application of EMD threshold filtering for fiber optical gyro drift signal denoising[J]. Acta Optical Sinica, 2015, 35(2): 0207001.

[10] 崔冰波, 陈熙源. 基于一种改进EMD算法的GPS多径效应抑制方法[J].中国惯性技术学报, 2014, 22(3): 346-351. Cui Bing-bo, Chen Xi-yuan. Multipath mitigation of GPS signal based on improved EMD algorithm[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 346- 351.

[11] Flandrin P, Rilling G, Gonçalvès P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters, 2004, 11: 112-114.

[12] He H L, Wang T Y, Leng Y G, et al. Study on non-linear filter characteristic and engineering application pf cascaded bistable stochastic resonance system[J]. Mechanical Systems and Signal Processing, 2007, 21: 2740 -2749.

[13] Colominas M A, Schlotthauer G, Torres M E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing[J]. Biomed. Signal Process. Control, 2014, 14(1): 19-29.

[14] Cui B, Chen X. Improved hybrid filter for fiber optic gyroscope signal denoising based on EMD and forward linear prediction[J]. Sensor and Actuators A: Physical, 2015, 230: 150-155.

[15] Komaty A, Boudraa A O, Augier B, Daré-Emzivat D. EMD-based filtering using similarity measure between probability density function of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27-34.

[16] 崔冰波, 陈熙源. 光纤陀螺温度漂移的多尺度集成建模研究[J]. 仪器仪表学报, 2015, 36(2): 304-309. Cui Bing-bo, Chen Xi-yuan. Study on multi-scale ensemble modeling of FOG temperature drift[J]. Chinese Journal of Scientific Instrument, 2015, 36(2): 304-309.

[17] Gan Y, Sui L F, Wu J F, et al. An EMD threshold de-noising method for inertial sensors[J]. Measurement, 2014, 49: 34-41.

Fiber optic gyro signal processing based on empirical mode probability distribution

CUI Bing-bo1, CHEN Xi-yuan1, GONG Zheng-yang2
(1. Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology, Ministry of Education, School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. Chongqing Yanfeng Plastic Omnium Faway Automotive Exteriors Co., Ltd., Chongqing 401120, China)

Based on an improved empirical mode decomposition (EMD) and a newly proposed mode selection criterion, an adaptive interval threshold filtering method is developed to mitigate the random drift of fiber optic gyroscope. First, the effect of adding Gaussian noise to assist EMD decomposition is analyzed, and a bounded assist is developed to improve decomposition quality. Then, aiming at the probability distribution feature of intrinsic mode function, a novel mode selection criterion is proposed. Finally, an adaptive interval threshold filter is developed based on data-driven threshold selection. The experiment analysis, which employs static data detected from an interferometric FOG, is performed to verify the proposed algorithm, and the results show that, compared with threshold filtering methods based on stationary wavelet transform (SWT) and EMD, the proposed method significantly improves the denoising result. In addition, the simulation results show that, compared with SWT-based method, the proposed method improves the heading accuracy of strapdown inertial navigation system by 78.6% in term of mean square error.

fiber optic gyroscope; empirical mode decomposition; probability density function; sample entropy

V241.5

：A

2015-05-19；

：2015-09-10

国家自然科学基金（51375087，50975049），江苏省普通高校研究生科研创新计划资助项目（KYLX_0106）

崔冰波（1986—），男，博士研究生，从事光纤陀螺信号处理及组合导航技术研究。E-mail: cuibingbo@163.com

联 系 人：陈熙源（1962—），男，教授，博士生导师。E-mail: chxiyuan@seu.edu.cn

1005-6734(2015)05-0690-06

10.13695/j.cnki.12-1222/o3.2015.05.023