箭载GPS定位临近地面卫星对流层延迟改正模型

饶爱水，李清梅，胡 健，吴关鹏

（中国卫星海上测控部，江阴 214431）

箭载GPS定位临近地面卫星对流层延迟改正模型

饶爱水，李清梅，胡 健，吴关鹏

（中国卫星海上测控部，江阴 214431）

针对经典对流层延迟改正模型无法处理负仰角卫星误差修正的问题，在传统球对称标准大气模型的基础上，采用射线描迹法建立了GPS信号穿透对流层的数学模型，推导了根据对流层折射最低点海拔高度计算对流层延迟改正的计算公式；为求解对流层折射最低点海拔高度，采用最小二乘法求得 GPS信号穿透对流层时地心张角与最低点海拔高度之间的线性方程，提出了根据卫星和火箭之间的夹角与地心张角之间的关系进行迭代计算，进而求得最低点海拔高度的方法；最后引入了模型误差因子，评估对流层延迟改正模型的效果。采用火箭飞行试验数据对模型进行验证，结果表明，该模型提供的方法能够消除负仰角卫星大部分对流层延迟，消除的最大延迟可达135 m，消除对流层延迟后的临近地面卫星参与定位计算使最终定位精度提高25 m，计算迭代次数平均10次，尤其适合箭载GPS实时定位。

折射指数；折射率；地心张角；射线描迹；大气折射

经典的对流层延迟改正模型包括Hopfield模型、Saastamoinen模型、Black模型等直接计算模型，也包括CFA模型、Chao模型、Niell模型等利用映射函数计算模型[1]，适用于仰角大于5°的情况，部分文献研究了在仰角在0°和5°之间的对流层改正模型[2]，网络差分对流层误差内插模型也被大量研究[3]，但对于负仰角的对流层延迟改正尚缺乏研究。运载火箭飞行高度通常超过对流层最大高度（60 km），对于仰角大于0°的卫星，对流层延迟改正为0 m；对于仰角小于0°且贴近地面的卫星，由于无线电波穿透整个对流层，对流层延迟改正数可达上百米。贴近地面卫星对最终定位结果的精度影响很大，采用卫星动态遮蔽角[4]可有效屏蔽贴近地面卫星对定位结果的影响，但减少了参与定位卫星个数。本文基于射线描迹法[5-6]，研究了GPS信号穿透对流层时的延迟改正模型，提出了根据对流层折射最低点海拔高度计算延迟改正的方法。

1 对流层穿透大气折射模型

在球对称的大气模型下，采用射线描迹法，考虑贴近地面卫星信号穿透对流层进入箭载GPS接收机的情况。图1把大气示意为两层，GPS卫星从G点发出无线电波，在A′2点进入大气层，经过大气折射最低点A0，从A1点进入第2层大气，大气层外缘A2点穿出，进入位于R点的接收机。A0、A1、A2点距离地心的距离分别为r0、r1、r2，在A1、A2点的大气入射角分别为z1、z2,对应的出射角分别为z′1、z′2，[A0, A1）、[A1，A2）之间的大气折射指数分为n1（A0点的折射指数）、n2（A1点的折射指数），A0A1、A1A2的长度分别为l1、l2，对应的地心张角分别为c1、c2。根据Snell定律[7]，有：

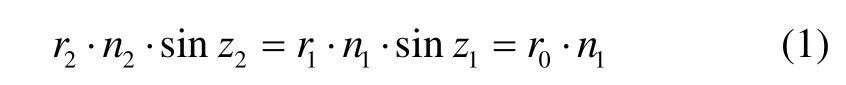
在△OA1A2中，

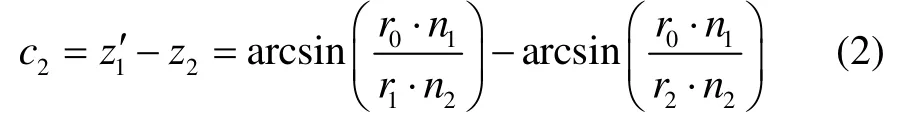
对应的折线长度为

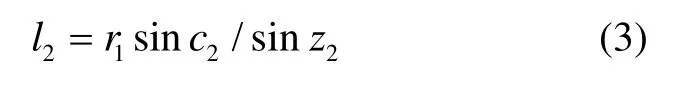
图 1 箭载GPS信号穿透对流层示意图Fig.1 On-board GPS signals penetrate through troposphere

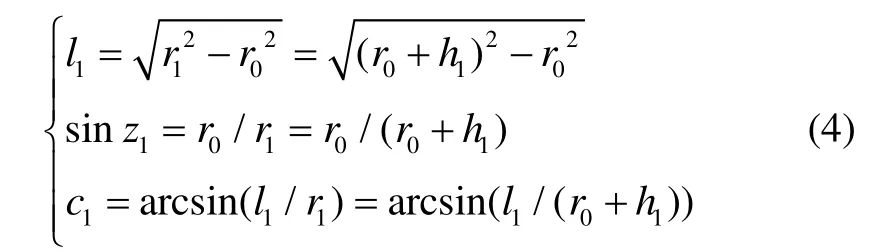
当大气被划分为m层时(2≤ i≤m )，有：

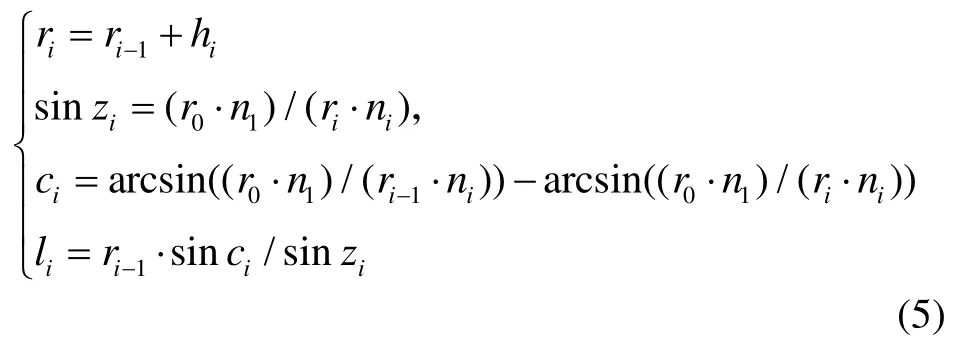
定义Vtrop为对流层延迟，根据对流层延迟计算公式[1]，有：

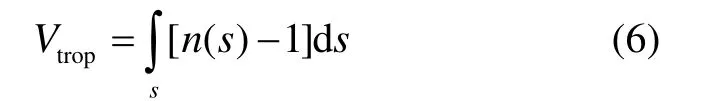
式中，S为电磁波在大气中传输的路径，n(s)为路径上的大气折射指数。在球对称的m层大气模型下，上式可近似为

路径S对应的地心张角Cs为

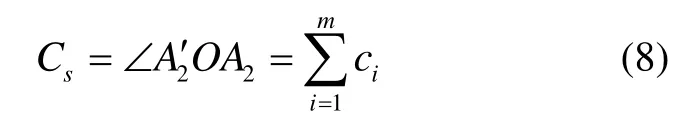
2 对流层延迟计算

根据大气折射率计算公式[7]：

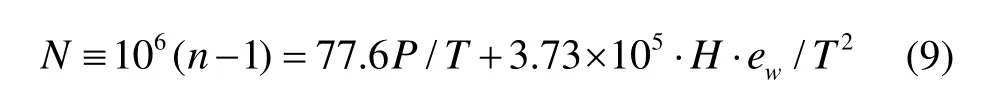
式中，

其中：h为大气的海拔高度，单位m；P为大气气压，单位为100 N/m2；T为大气绝对温度，单位K；t为大气温度，单位℃。本文采用ICAO（国际民航组织）标准大气模型[8-9]计算大气压力和温度，得到的大气折射率符合负指数模型[10-11]，在海平面的折射率为311，在35 km高空的折射率为1.6。

给定电波射线距离地心最低点的地心距r0和大气分层厚度hi( i=1～m)后，可计算得出对流层延迟。图2示意了对流层延迟与最低点海拔高度 h0(其中h0=r0-ae)的关系，最外层大气的海拔高度取60 km，大气厚度设为10 m时的计算结果，对应的地心张角如图3中的曲线Cs所示。

图3描述对流层延迟取对数后与h0的线性关系，用分段函数拟合，得到如下的公式：

图3还描述了地心张角Cs（单位弧度）与最低点海拔高度h0（单位m）的线性关系，最小二乘法拟合得到的公式如下：

图 2 对流层延迟随最低点海拔高度变化曲线Fig.2 Relationship between tropospheric delay and lowest altitude

图3 地心张角及对流层延迟与最低点海拔高度的线性关系Fig.3 Linear relationship between geocentric angle, tropospheric delay and the lowest altitude

3 对流层折射最低点确定方法

当运载火箭飞行高度大于对流层高度时，大气折射率为1，设运载火箭距离地心的距离为rR，最外层大气距离地心的距离为点和Am点应用公式(1)，有：

式中，rG为GPS距离地心的距离。根据公式(12)、(14)、(15)，可以计算得出GPS卫星、地心、运载火箭三者之间的夹角：

在导航定位计算过程中，容易得到上一次的GPS卫星和运载火箭的位置。在△GOR中，利用余弦定理，有：

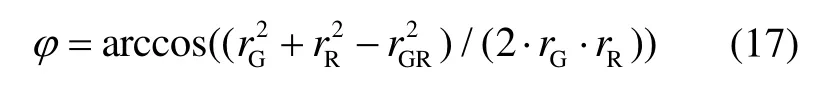
式中，rGR为GPS与运载火箭的直线距离。

根据公式(16)和(17)，利用迭代法可以算出电波射线距离地心最低点的地心距r0，进而根据公式(11)计算得出电离层延迟的大小。

4 对流层延迟计算结果

分析火箭飞行试验数据，采用内符合精度[12]分析方法得到跟踪弧段内火箭的位置精度，不考虑对流层延迟改正时得到的结果如图4所示，图中两处波峰分别由2号卫星和5号卫星穿透对流层引起。采用本文提供的对流层延迟改正方法，得到的对流层延迟改正值和最低点海拔高度如图5所示，其中最低点海拔高度迭代计算的平均次数为10次，定位精度如图6所示。

图5表明，对流层延迟改正最大值为135 m，电波折射最低点的海拔高度为6.8 km；图6表明，采用本文的方法，GPS定位精度从48 m提高到23 m。

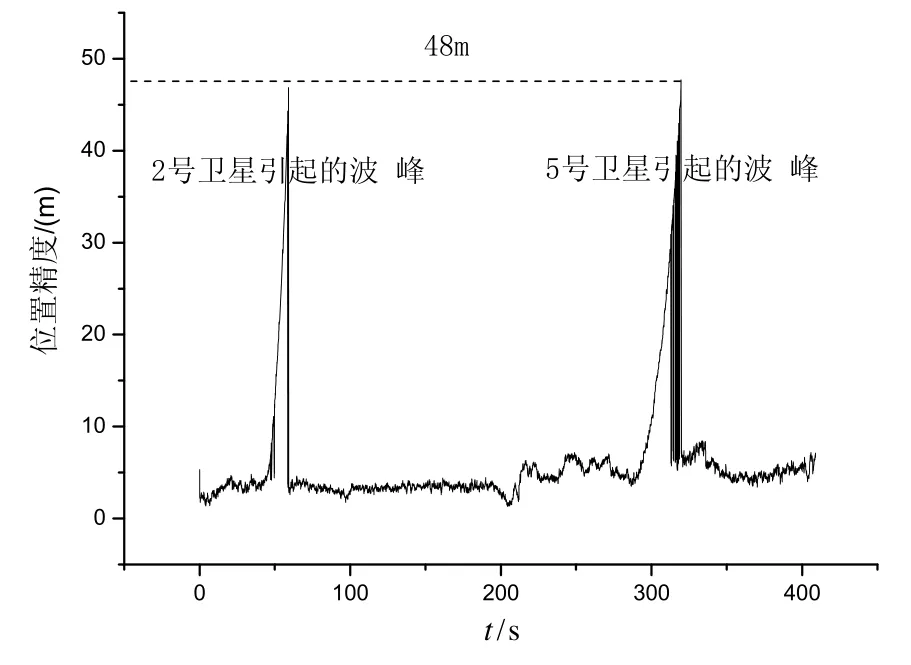
图 4 箭载GPS位置精度原始曲线图Fig.4 Original precision of on-board GPS position

图 5 对流层延迟改正值及最低点海拔高度关系曲线Fig.5 Relationship between tropospheric delay correction and lowest altitude

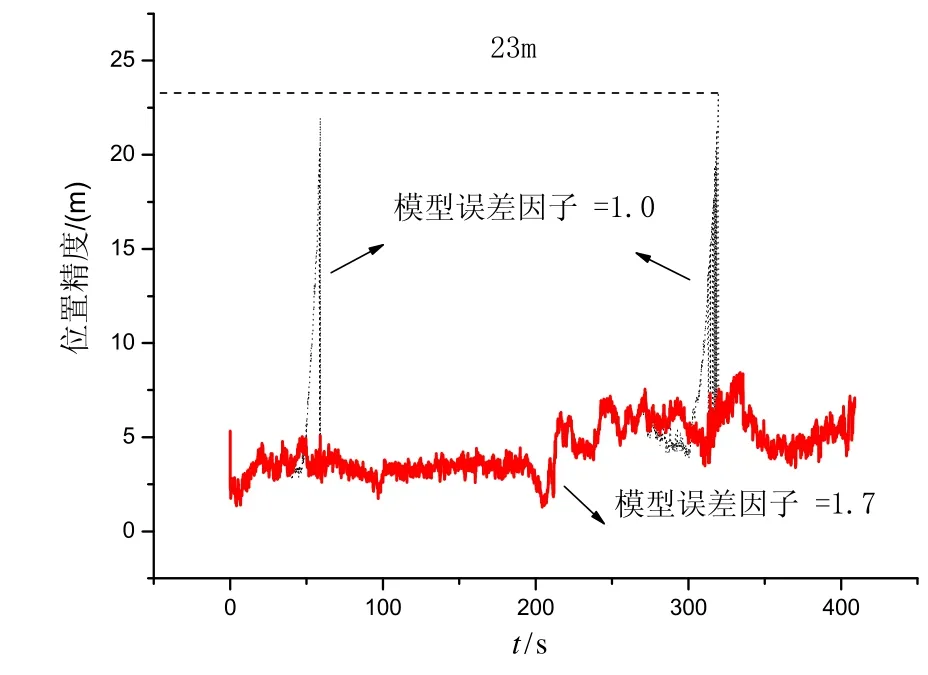
图 6 箭载GPS定位对流层延迟改正后的位置精度曲线Fig.6 Precision of on-board GPS after tropospheric delay correction

引入模型误差因子mσ ，对公式(11)的结果进行修正：

式中，V表示大气层延迟总误差，包括对流层延迟和电离层延迟，模型误差因子包含了电离层延迟误差、球对称大气模型误差以及大气折射率计算模型误差等。图6显示了σm分别为1.0和1.7的情况，当σm=1.7时，大气折射误差修正被消除，定位精度与屏蔽2号卫星和5号卫星的结果相同。

5 结 论

本文在国际民航组织标准大气模型的基础上，采用标准气象元素计算了大气折射率，采用射线描迹法对箭载GPS定位时电波穿透对流层进行分析，采用分层求和方法得到了对流层延迟改正与对流层折射最低点海拔高度之间的计算公式，对流层延迟最大可达200 m；通过线性拟合的方法，发现了电波穿透对流层对应的地心张角与最低点海拔高度之间的线性方程，地心张角最大可达17°；提出了根据卫星和火箭之间的夹角与地心张角之间的关系进行迭代计算，进而求得最低点海拔高度的方法。

采用火箭飞行试验数据对该方法进行了验证，结果表明，该方法能有效修正对流层延迟，计算方法简单，适合箭载GPS实时定位。引入了模型误差因子，以表征误差改正的实际效果，采用内符合精度作为误差修正效果的依据。由于未考虑电离层延迟改正，导致模型误差因子较大，下一步将研究临近地面的负仰角卫星的电离层延迟改正方法。

（References）：

[1] 赵铁成, 韩曜旭. GPS定位系统中几种对流层模型的探讨[J]. 全球定位系统, 2011(1): 46-52. Zhao Tie-cheng, Han Yao-xu. Study on several tropospheric models in GPS positioning system[J]. GNSS World of China, 2011(1): 46-52.

[2] 段成林, 马传令, 曹建峰, 等. 一种低仰角对流层折射修正的新方法[J]. 红外与激光工程, 2012, 41(5): 1195-1199. Duan Cheng-lin, Ma Chuan-ling, Cao Jian-feng, et al. A new method on tropospheric refraction correction at low elevation[J]. Infrared and Laser Engineering, 2012, 41(5): 1195-1199.

[3] 潘树国, 王姗姗, 沈雪峰, 等. 顾及高程差异的网络差分对流层误差内插模型[J]. 中国惯性技术学报, 2012, 20(2): 192-195. Pan Shu-guo, Wang Shan-shan, Shen Xue-feng, et al. Interpolation model for troposphere delay error on network differential considering elevation difference[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 192-195.

[4] Rao Ai-shui, Li Yong-gang, Hu Jian, et al. Dynamic calculation method of satellite elevation mask with rocket onboard GPS real-time positioning[C]//China Satellite Navigation Conference 2014 Proceedings. 2014: 27-34.

[5] 李德鑫, 杨日杰, 孙洪星, 等. 基于射线分层算法的电磁波大气吸收衰减特性分析[J]. 电讯技术, 2012, 52(1): 80-85. Li De-xin, Yang Ri-jie, Sun Hong-xing, et al. Characteristic analysis of atmospheric absorption and attenuation based on rays layering algorithm[J]. Telecommunication Engineering, 2012, 52(1): 80-85.

[6] Wu X L, Hu X G, Wang G, Zhong H J, Tang C P. Evaluation of COMPASS ionospheric model in GNSS positioning[J]. Advances in Space Research, 2012, 51(6): 959-968.

[7] Mcgraw G A. Tropospheric error modeling for high integrity airborne GNSS navigation[J]. Position Location and Navigation Symposium, 2012(4): 158-166.

[8] Rohm W, Bosy J. The verification of GNSS tropospheric tomography model in a mountainous area [J]. Advances in Space Research, 2011, 47(10): 1721- 1730.

[9] Awange J L, Wickert J, Schmidt T, Sharifi MA, Heck B, Fleming K. GNSS remote sensing of the Australian tropopause[J]. Nature Climate Change, 2011, 105: 597-618.

[10] Wang X Y, Wang X L, Dai Z Q, Ke F Y, Cao Y C, Wang F F, Song L C. Tropospheric wet refractivity tomography based on the BeiDou satellite system[J]. Advances in Atmospheric Sciences, 2014.

[11] Bender M, Stosiusa R, Zusa F, et al. GNSS water vapour tomography-expected improvements by combining GPS, GLONASS and Galileo observations[J]. Advances in Space Research, 2011, 47(5): 886-897.

[12] Ren Chao, Peng Jia-di, She Di. Effects of low GPS satellite elevation mask angle on estimation of tropospheric delay[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 125-127.

Tropospheric delay correction model of near ground satellite position using on-board GPS

RAO Ai-shui, LI Qing-mei, HU Jian, WU Guan-peng
(China Satellite Maritime Tracking and Controlling Department, Jiangyin 214431, China)

In view that classical tropospheric delay correction model cannot deal with deviation correction of negative elevation angel satellite, the phenomenon when GPS signal penetrate troposphere using radar ray tracing was modeled based on traditional spherical symmetry standard atmosphere model, and the formulas for computing the correction of tropospheric delay was deduced based on the lowest altitude of troposphere reflection. To calculate the lowest altitude of tropospheric refraction, the liner equation between geocentric angel and the lowest altitude when GPS signal penetrate troposphere was obtained by using least square method. Then a method for calculating the lowest altitude was proposed based on iterative computation using the relationship between the angle of satellite-to-rocket and the geocentric angel. Finally the efficiency of tropospheric delay correction model was evaluated by introducing the model’s error factor. The test data of rocket flight were used to validate the model, and the result proves that the proposed method can eliminate most of the tropospheric delay of up to 135 m, and improve the precision of the near ground satellite position of up to 25 m. This method is especially appropriate to real-time positioning of on-board GPS.

refractive index; refractivity; geocentric angle; ray tracing; atmospheric refraction

V19

：B

2015-05-15；

：2015-08-25

饶爱水（1980—），男，工程师，从事航天测控研究。E-mail：lqmei03@163.com

1005-6734(2015)05-0670-04

10.13695/j.cnki.12-1222/o3.2015.05.019