小子样条件下某型加速度计步降加速寿命试验优化设计

罗 赓，穆希辉，牛跃听，杜峰坡，陈建华，王永南

（1. 中国华阴兵器试验中心，陕西 华阴 714200；2. 军械技术研究所，石家庄 050003；3. 军械工程学院，石家庄 050003）

小子样条件下某型加速度计步降加速寿命试验优化设计

罗 赓1,3，穆希辉2，牛跃听2，杜峰坡2，陈建华3，王永南3

（1. 中国华阴兵器试验中心，陕西 华阴 714200；2. 军械技术研究所，石家庄 050003；3. 军械工程学院，石家庄 050003）

为了解决小样本条件下某型加速度计进行步降应力加速寿命试验的方案优劣难以评估的难题，提出一套适合于工程应用的优化设计方法。首先针对自然贮存试验的统计数据，采用基于极小卡方估计和拟合优度检验相结合的贮存可靠性评估方法以及最小二乘法建立寿命分布模型和加速方程。然后进行高温老化试验，依据失效模式分析机制和已建的失效树确定加速应力上限，完善加速寿命试验先验知识。最后对试验样本量进行可信度评定并根据先验知识采用基于思维进化算法优化BP神经网络的仿真方法进行优化设计，得到最优试验方案并通过试验进行验证。结果表明，该最优试验方案计算得到的先验参数值与原值之间的相对误差不超过1.7%，可以满足工程应用。

加速寿命试验；优化设计；步降应力；小子样；加速度计

某型加速度计是某型号导弹惯导平台提供运动载体加速度信息的关键部件[1]，是长期自然储存过程中的薄弱环节。对其进行寿命评估非常重要。然而试验方案的优劣决定了加速试验的精度与效率。传统的寿命评估采用基于监测的自然环境试验寿命评估方法，耗时耗力耗钱[2]，远远不能满足加速度计贮存可靠性评估的迅速性和准确性，须采用加速试验进行寿命评估，然而试验方案的优劣决定了加速试验的精度与效率。

如何进行加速试验方案优化设计是目前可靠性试验领域的研究热点。文献[3-5]采用解析法来获取最优方案，解析法可以得到试验方案具体的解析解，但若设计变量的维数较多的话，其建模与分析推理会显得十分困难复杂，而且在很多场合下解析方法难以得到或者不能得到最优方案，很不适合于工程应用。文献[6-7]提出了一种基于Monte-Carlo仿真的加寿命试验优化设计方法，该方法以仿真、分析和优化为主线，将加速试验优化设计问题转换为Monte-Carlo仿真试验数据的统计分析问题，避免了解析法需要进行精度指标分析这一复杂繁琐的过程，极大降低了优化设计的难度，简化了优化设计的过程，更利于流程化的实现，但是仍存在小子样条件下试验可信度不确定，试验仿真规模大等问题。基于此，本文以加速度计为实例，提出一种适合于工程应用的加速寿命试验优化设计方法，可以为加速度计这类的机电产品的加速试验提供参照依据。

1 模型建立

1.1 自然贮存试验数据统计

该型加速度计贮存于我国各地的仓库内，覆盖范围十分广泛，包括亚热带、温带、寒带三个气候带。依据仓库所处地域的年平均温度，选取A(21.38℃)、B(14.88℃)、C(6.78℃)三个温度差别较大的地域库进行加速度计检测结果统计，其中统计结果如表1所示。

通过对加速度计自然贮存数据进行系统分析发现：湿度对于寿命的影响从数据规律上难以体现，因此认定主要环境应力为温度应力。

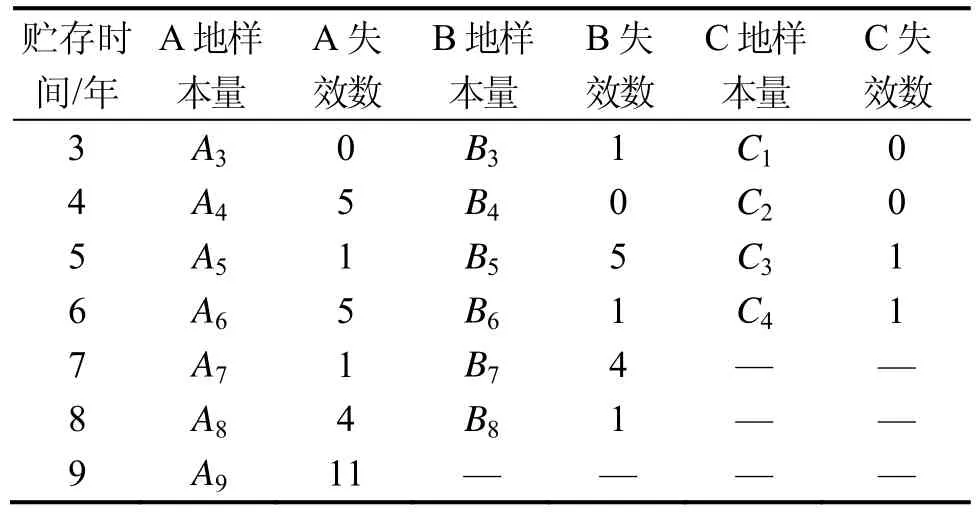
表1 加速度计检测结果Tab.1 Detection result of accelerometer

1.2 计算结果

以A库为例，取0.95为给定的可靠度下限，置信度为0.9。根据表1的试验数据，采用基于极小卡方估计和拟合优度检验相结合的贮存可靠性评估方法[8]，可以得出不同分布类型相应的χ2统计量值、拟合优度p值以及失效分布函数中的未知参数值，具体结果如表2所示。由表2得出A库加速度计的寿命分布服从威布尔分布：

同理B、C两库加速度计经计算亦服从威布尔分布：

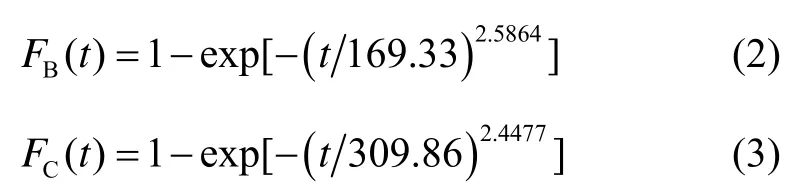
三个地域库加速度计的寿命分布函数具有基本不变的形状参数，这一点符合“各温度应力水平下，产品失效机理不变”这一假设。故该加速度计的寿命分布函数中的形状参数可取其平均值2.4602，其特征寿命，采用最小二乘法，可得表征其特征寿命的加速模型：

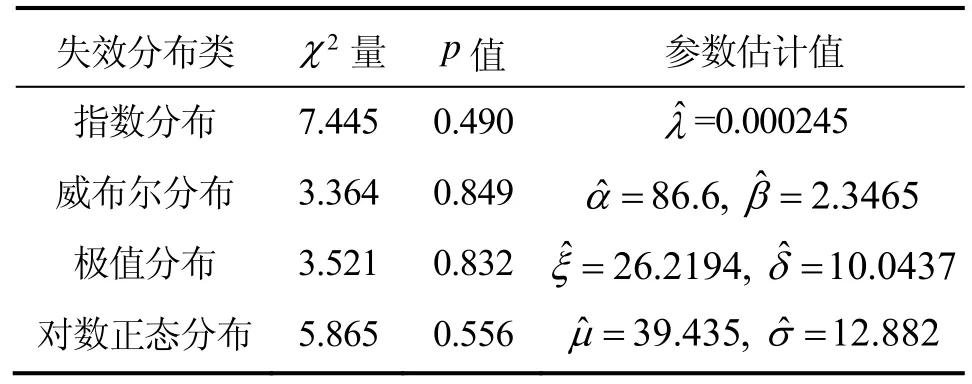
表2 加速度计不同失效分布相关计算结果Tab.2 Result of different distribution patterns

2 小样本条件下可信度评定

作为产品加速试验的一个难点，试验样本的数量直接影响着产品可靠性评估的精度，样本量愈大，加速试验得到的试验数据愈多，产品可靠性评估愈精确。然而由于试验时间和试验费用等方面的限制，加速试验要求在保证一定精度的前提下，试验样本数量最小。在一定精度指标δ和最小样本数量n下，试验结果的置信水平1-γ可由式(5)得出：

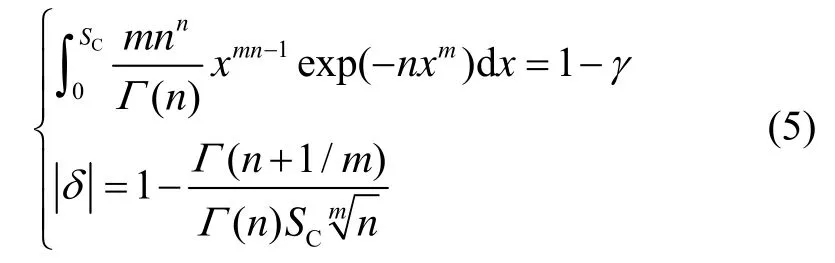
式中，SC为置信系数，m为形状参数，n为最小样本数量，δ为算值与实际值相对误差期望值。

当精度指标δ为0.05时，可得样本量n与置信水平1-γ的关系如表3所示。依据GJB2515-95得到机电装置的置信水平一般在 0.7～0.8之间，因此样本量必须大于3。然而当样本量n增大时，虽然置信水平1-γ亦会提高，但是相应的试验成本也明显提高，故需综合考虑可靠度、精度指标δ、置信水平1-γ以及试验成本等参数指标，确定加速试验需要的样本量。

表3 小子样条件的置信水平Tab.3 Confidence level of small samples

3 加速应力上限确定

由于经费等多方面的限制，只能选取两个样本进行摸底试验。依照公式(5)可知，置信水平1γ -远低于弹载机电装备的置信度水平，对它们进行加速寿命试验进而得到加速度计的先验模型参数是不可信的，但是可以通过开展高温老化试验来确定加速应力上限：运用物理失效机理判断加速度计在试验下的故障模式是否与之前的故障模式一致，进而定性确定满足加速机理一致性的应力上限。

采用湿热试验箱和通用检测平台进行试验，综合考虑GJB5103-2004和其它加速度计的性能指标：将1#加速度计放入1#试验箱，试验条件设为温度85℃，湿度75%rh；2#加速度计放入2#试验箱，试验条件设为温度75℃，湿度75%rh。环境条件设定完毕后进行试验。通用检测平台定期对加速度计的性能参数进行检测用来判断其是否失效，当两加速度计均失效时停止试验。依据失效模式分析机制和已建的加速度计失效树对失效加速度计进行失效分析，可以得到两条重要结论：

① 样本失效是由于高温使其内部 A型电容工作异常造成的，可以判断主要环境应力为温度应力，与自然条件下贮存可靠性试验结论相吻合。

② 两个加速度计虽然在湿度一致、温度不一致的情况下失效，但是通过分析可知两者均为内部A型电容工作异常，分析其失效机理，未出现失效机理不一致的现象，因而认定其最高工作温度应力水平为85℃。

4 试验优化设计

4.1 加速度计先验知识

① 寿命分布函数

该加速度计寿命服从Weibull分布：

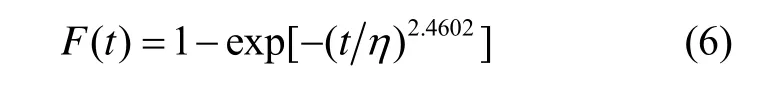
其中t的单位为年。

② 加速模型

该加速度计加速方程为Arrhenius方程：

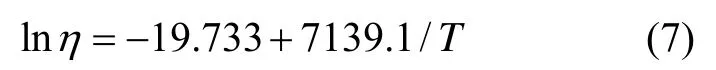
其中T的单位为开尔文。

③ 试验应力水平

结合GJB5103-2004和高温老化试验结论，加速度计最高温度确定为85℃，最低温度拟选范围为50℃～70℃。

4.2 试验基本变量

根据试验的实际情况，确定试验设计变量如下：

① 样本量n

考虑到试验经费和加速度计的实际情况，该加速寿命试验属于小子样情况，结合公式(5)，提供能满足统计分析精度指标要求的样本量8个。

② 应力水平数k

由于试验样本量n的限制，结合GJB5103-2004，本试验选择四个应力水平，即 k=4。温度应力采用倒数等间隔取值方法。

4.3 试验优化变量

为降低计算量，对设计变量进行简化：① 应力水平Si，i=1,…,k；② 应力水平Si下的失效截尾数ir，i=1,…,k。

4.4 约束条件

经分析，约束条件如下：

① 应力水平数k满足k＜n；

② 应力水平Si需满足

4.5 目标函数

在满足模型假设的前提下，利用加权系数[9]将正常使用应力水平下的对数 p阶分位寿命渐近方差（Avar）估计（精度函数）与试验时间（费用函数）结合起来构成目标函数。正常使用应力水平下的对数 p阶分位寿命渐近方差为

式中，ζp0为正常应力水平S0下对数p阶分位寿命。

在此类型试验中，子试验的截尾时间决定了试验时间。但由于其随机性，故应考虑用试样在各应力水平下的特征寿命之和来代替费用函数，即

基于此，目标函数最终可以表示为

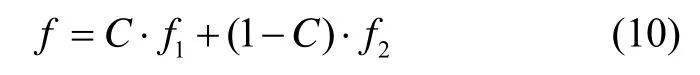
4.6 优化算法

图1为基于Monte-Carlo仿真的SDSALT试验优化设计流程图，具体流程：

① 依据试验约束条件构造包含设计变量的备选SDSALT方案集P；

② 从P中选出一个试验方案 pg，其中，G为方案集包含的试验方案数；

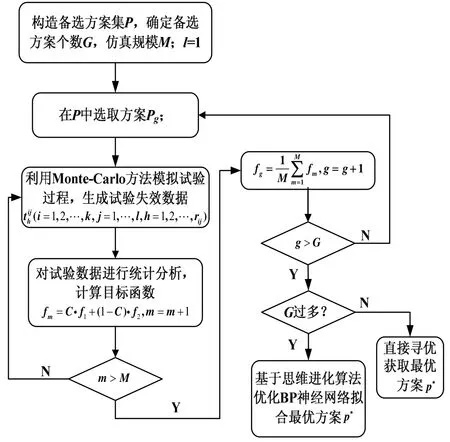
图1 SDSALT优化设计流程图Fig.1 Optimal design of step-down-stress accelerated life test

③ 利用蒙特卡洛法仿真模拟选定的SDSALT方

④ 对数据集中的每组失效时间数据进行统计分析，分别计算其精度函数f1和费用函数f2，进而计算该组数据的目标函数 fm；

⑤ 利用式(11)计算选定SDSALT方案的目标函数值：

⑥ 返回②选取另外一个试验方案并重复③～⑤，直到所有的试验方案全部已选取，此时可得目标函数值集，即

⑦ 根据备选方案实际规模，对⑥得到目标函数值集进行目标直接寻优或者采用基于思维进化算法优化BP神经网络进行目标函数拟合间接寻优选取使目标函数值最小的试验方案作为最优试验方案p*。

4.7 思维进化算法优化BP神经网络拟合

精度问题与效率问题在试验优化设计中是一对矛盾体，要达到允许的精度，就需进行大量的模拟仿真，就会降低效率。针对加速试验优化设计在保证精度的前提下仿真规模普遍偏大的缺点，本文采用思维进化算法优化BP神经网络来对加速试验进行优化设计。

思维进化算法可以弥补BP神经网络存在的一些先天不足[10-11]，将两者结合起来，利用思维进化算法对BP神经网络的初始权值和阈值进行优化，大大加快了BP神经网络的训练速度，并且提高了BP网络训练的稳定性，为解决复杂问题提供了一个很好的方法途径。其具体设计流程（如图2所示）为：① 产生初始种群；② 将未优化的神经网络输出值与目标函数值的均方误差的倒数作为得分函数；③ 趋同、异化操作；④ 获取最优权值、阈值；⑤ 训练BP神经网络；⑥ 对目标函数进行仿真优化。

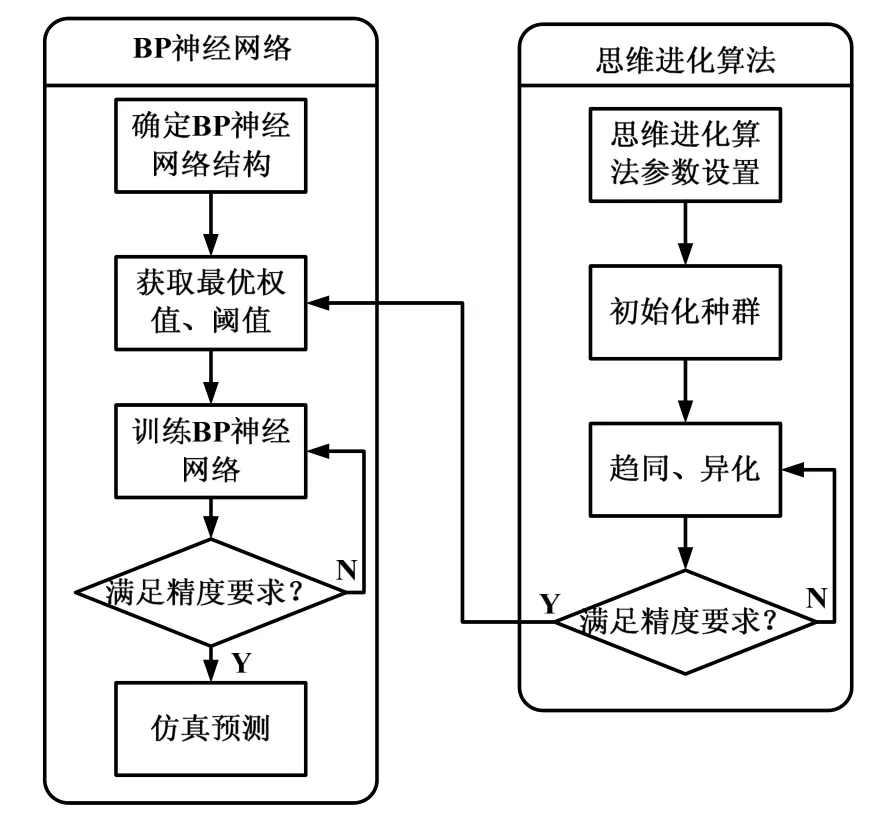
图2 MEA-BP神经网络设计流程图Fig.2 Design flowchart for MEA-BP neural network model

4.8 优化结果

若采用直接优化，备选方案过多（L=105），故采用基于思维进化算法优化BP神经网络对该加速度计步降加速寿命试验进行优化设计。此时备选方案为，其中最低温度水平Tmin，其余温度应力采用倒数等间距温度应力，取应力水平数 k=4，进行步降应力加速寿命试验，则

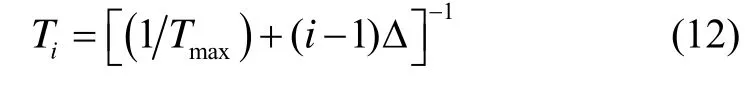
由工程经验可知每个应力水平下的试验样本量最少应为5个，但由于本试验中该型加速度计只有8个，属于小子样情况，因此结合实际情况与约束条件得到每个应力下的截尾数方案共有5组：{(5,1,1,1) (4,2,1,1) (3,3,1,1) (3,2,2,1) (2,2,2,2) }。其优化结果如图3所示。

从图3可看出目标函数在最低温度水平为59.5℃，各应力水平下截尾数为(4,2,1,1)时目标函数值最小，故该加速度计步降加速寿命试验方案如式(14)所示：

5 实例验证

为了验证所得试验方案是否能满足工程应用，按照优化设计方案，在湿热试验箱进行试验（其中湿度为75%rh），以加速度计性能参数零值偏差Δf (0g附近)为失效判据，通过通用检测平台（如图4所示）检测加速度计，得到加速度计输出信号频率，如图5所示。加速度计输出频率的最大值和最小值之间相差很小，通常将平均值作为检测结果记录到检测记录表得到试验原始数据，以检查数据是否处于400～800 Hz之间来判断是否失效，如此反复直到试验结束。

对得到的原始数据进行相应处理可以计算得到该试验方案相应的先验参数值，将其与原值比较，得到结果如表4所示。从表4可以看出，采用本文优化方法得到的试验方案进行试验，经处理计算得到的先验参数计算值与原值的相对误差不超过 1.7%，充分说明了本文所提方法考虑因素更加全面，在小子样条件下得出的试验方案更加合理，更加有效。

图4 通用检测平台Fig.4 General testing platform

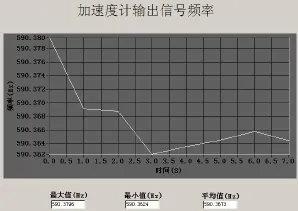
图5 加速度计输出信号频率Fig.5 Output signal frequency of accelerometer

表4 先验参数计算值与原值结果对比Tab.4 Comparision on results between calculated and original values

6 总 结

本文针小子样条件下某型加速度计步降加速寿命试验提出了一种基于思维进化算法优化 BP神经网络的Monte-Carlo仿真优化设计方法，针对给出的实例得到了最优试验方案，并通过实例进行了验证。结果表明该优化设计方法可以在小样本条件下，保证试验精度，极大降低了仿真试验的规模，提高了优化效率，证明了此算法的可行性与正确性，可以更好地满足工程应用的需求。

（References）：

[1] 袁宏杰, 李楼德, 段刚, 等. 加速度计贮存寿命与可靠性的步进应力加速退化试验评估方法[J]. 中国惯性技术学报, 2012, 20 (1): 113-116. Yuan Hong-jie, Li Loude, Duan Gang, et al. Storage life and reliability evaluation of accelerometer by step stress accelerated degradation testing[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 113-116.

[2] Jinsuk L, Pan Rong. Analyzing step-stress accelerated life testing data using generalized linear models[J]. IIE Transactions, 2010, 42(8): 589-598.

[3] Bai D S, Chun Y R. Optimum simple step-stress accelerated life tests with competing causes of failure[J]. IEEE Transactions on Reliability, 1991, 40(5): 622-627.

[4] Pascual F. Accelerated life test planning with independent weibull competing risks with known shape parameter[J]. IEEE Transactions on Reliability, 2007, 56(1): 85- 93.

[5] Li Xiao-yang, Jiang Tong-min. Optimal design for stepstress accelerated degradation testing with competing failure modes[C]// Proceedings of Annual Reliability and Maintainability Symposium, 2009: 64- 68.

[6] 潘刚, 梁玉英, 吕萌等. 小样本条件下步降加速退化试验优化设计[J]. 仪表技术与传感器, 2013(5): 91-93. Pan Gang, Liang Yu-ying, Meng Jun. et al. Optimization design of step-down-stress accelerated degradation test on condition of small sample[J]. Instrument Technique and Sensor, 2013(5): 91-93.

[7] 谭源源, 张春华, 汪春华, 等. 竞争失效场合仿真基加速试验优化设计方法[J]. 国防科技大学学报, 2011, 33(2): 130-135. Tan Yuan-yuan, Zhang Chun-hua, Wang Ya-shun, et al. Study on simulation based optimal design method for accelerated testing with competing failure modes[J]. Journal of National University of Defense Technology, 2011, 33(2): 130-135.

[8] 罗赓, 穆希辉, 牛跃听, 等. 温度应力下的加速度计贮存寿命评定[J]. 装甲兵工程学院学报, 2014, 28(3): 27-30. Luo Geng, Mu Xi-hui, Niu Yue-ting, et al. Storage life evaluation of accelerometer under temperature stress[J]. Journal of Academy of Armored Force Engineering, 2014, 28(3): 27-30.

[9] Yang Guang-bin. Optimum constant-stress accelerated life test [J]. IEEE Transactions on Reliability, 1994, 43 (4): 575-581.

[10] Li Song, Liu Li-jun, Huo Man. Prediction for short-term traffic flow based on modified PSO optimized BP neural network[J]. Systems Engineering--Theory & Practice, 2012, 32(9): 2045-2049.

[11] Xu Yi-shan, Zeng Bi, Yin Xiu-wen. et al. BP neural network and its applications based on improved PSO[J]. Computer Engineering and Applications, 2009, 45(35): 233-235.

[12] 李瑞, 汪立新, 刘刚, 等. 基于加速退化模型的加速度计非线性特征分析及贮存寿命预测[J]. 中国惯性技术学报, 2014, 22(1): 125-130. Li Rui, Wang Li-xin, Liu Gang, et al. Nonlinear characteristic analysis and storage life forecast for accelerometer based on accelerate degradation model[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 125-130.

Optimal design method for accelerometer step-down-stress accelerated life testing on condition of small sample

LUO Geng1,3, MU Xi-hui2, NIU Yue-ting2, DU Feng-po2, CHEN Jian-hua3, WANG Yong-nan3
(1. Ordnance Test Center, Huayin 714200, China; 2. Ordnance Technological Research Institute, Shijiazhuang 050003, China; 3. Ordnance Engineering College, Shijiazhuang 050003, China)

An optimal design method is presented for accelerometer step-down-stress accelerated testing on condition of small sample. Firstly, the storage reliability evaluation method combining minimum chi-square estimation, goodness fit of test and the least square method are used to establish lifetime distribution function and acceleration equation for the statistical data of natural storage environmental test. Secondly, the accelerated stress upper bound is determined based on the failure mode analysis mechanism and the failure tree though high-temperature aging testing. Finally, the credibility evaluation is made for the test sample size, and an optimal experiment scheme is carried out based on MEA-BP neural network for Monte-Carlo simulation. The results show that the relative error between the prior parameter value calculated by the optimal scheme and the original values is less than 1.7%, meeting the requirements of the engineering applications.

accelerated life testing; optimal design; step-down-stress; small sample; accelerometer

TP114.3

A

2015-06-14；

：2015-09-28

国家自然科学基金（61471385）

罗赓（1990—），男，工程师，主要从事可靠性工程研究。E-mail：luo13618234910@163.com

联 系 人：穆希辉（1963—），男，教授，博士生导师。E-mail：luo13618234910@163.com

1005-6734(2015)05-0696-05

10.13695/j.cnki.12-1222/o3.2015.05.024