基于强跟踪滤波器的SINS大失准角初始对准新方法

彭 卓，张 嵘，郭美凤，刘 刚，罗寿红

（1. 清华大学 精密仪器系，北京 100084；2. 中国航天员科研训练中心，北京 100094）

基于强跟踪滤波器的SINS大失准角初始对准新方法

彭 卓1,2，张 嵘1，郭美凤1，刘 刚1，罗寿红1

（1. 清华大学 精密仪器系，北京 100084；2. 中国航天员科研训练中心，北京 100094）

捷联惯性导航系统静基座初始对准时一般先进行粗对准，使失准角缩小到一定范围内从而满足小失准角假设下的线性误差模型，然后再进行精对准。在不进行粗对准时失准角一般为大角度，需要采用复杂的非线性误差模型和非线性滤波方法。研究发现通过设置合理的误差协方差矩阵初值，采用反馈校正滤波结构，并引入强跟踪滤波算法可以在大失准角情况下既无需粗对准，又无需采用非线性模型来实现精对准。仿真结果表明，该方法可以实现大失准角初始对准，鲁棒性好，在任意姿态初值下都可以使航向角在300 s内收敛到0.05°的理论极限精度，与小失准角精对准方法的速度和精度相当但省去了粗对准因而耗时更短，与无迹卡尔曼滤波在600 s时才收敛到0.5°的速度相比大为改善。

捷联惯性导航；初始对准；大失准角；强跟踪滤波器

捷联惯性导航系统（Strapdown Inertial Navigation System，SINS）本身是一个积分系统，积分初值对导航结果的影响巨大。初始对准就是在导航开始前确定载体初始姿态的过程，对导航精度至关重要。SINS静基座初始对准通常采用标准卡尔曼滤波器（Kalman Filter，KF），滤波模型采用小失准角假设下的线性误差模型。在实际使用中，为了满足小失准角假设，必须先进行粗对准，使姿态误差缩小到一定范围内，然后才能采用KF进行精对准。常用的粗对准方法为解析式粗对准[1]，为了提高精度通常需要取一段时间的平均值，这不仅增加了步骤，还增加了时间。如果不进行粗对准，失准角一般为大角度，此时线性误差模型已经失效，需要采用非线性误差模型和非线性滤波方法。例如刘海鹏采用扩展卡尔曼滤波（ExtendedKalman Filter，EKF）和无迹卡尔曼滤波（Unscented Kalman Filter，UKF）进行大失准角初始对准并仿真验证了随着失准角的增大UKF比EKF估计精度更高[2]；龙瑞采用中心差分卡尔曼滤波器（Central Difference Kalman Filter，CDKF）并仿真验证了在大失准角条件下CDKF比EKF和UKF具有更高的精度[3]；Jamshaid提出二阶分离插值滤波器（Second-order Divided Difference filter，DDF2）在航向大失准角初始对准中能够获得比EKF和UKF更高的姿态精度[4]；Wu采用基于奇异值分解的容积卡尔曼滤波器（Cubature Kalman Filter，CKF）进行大失准角初始对准获得了比UKF更高的精度和更快的速度[5]。但是，以上这些非线性滤波方法都存在两个问题：一是算法复杂，计算量比标准卡尔曼滤波大的多；二是非线性滤波都存在近似系统模型或者近似概率分布的问题，不是最优滤波器，特别是在失准角已经满足小角度假设时非线性滤波不如标准卡尔曼滤波精度高。针对以上问题，本文提出一种大失准角初始对准新方法，该方法仍然采用线性模型，通过设置合理的滤波初值，采用反馈校正并创新性的引入强跟踪滤波器来实现大失准角情况下的直接精对准。该方法与传统粗对准+精对准方法相比不仅省去了粗对准，节省了时间，还保持了标准卡尔曼滤波器能达到的精度，与一般非线性滤波方法相比不仅不需要进行复杂的非线性滤波计算，还具有更高的精度、更快的速度和更小的计算量，是一种非常实用的大失准角初始对准解决方案。

1 系统模型

一般所谓的失准角指的是n系到n′系的小角度旋转矢量，与转动次序无关。而在大失准角情况下，根据有限转动的不可交换性，需要定义大失准角的转动次序。本文定义大失准角的转动次序为：n系绕z轴转ϕz角到n1系，n1系再绕x1轴转ϕx角到n2系，n2系再绕y2轴转ϕy角到n′系。记大失准角可以推出大失准角情况下 SINS姿态误差和速度误差方程分别如式(1)和式(2)所示[6]：

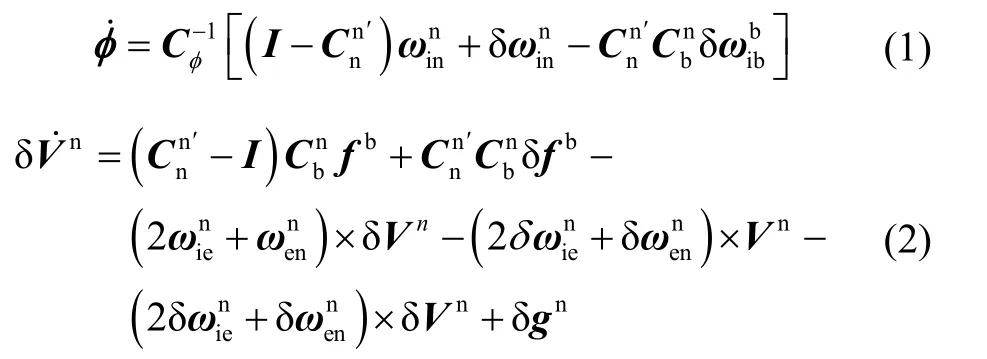
2 算法原理

2.1 反馈校正技术

以上卡尔曼滤波模型是在小失准角假设下推导出来的，要用它来解决大失准角非线性模型的初始对准问题，首要解决的问题是如何让系统迅速收敛到小失准角范围内。联想到在罗经法对准中，虽然罗经对准算法是在小失准角假设下推导出来的，但是在大失准角时依然适用[7]，究其原因在于在大失准角情况下，虽然线性模型中的罗经项与真实的非线性罗经项不同，但是它们反馈之后对系统的校正方向是相同的，因此通过反馈可以逐渐将系统“拉回”到小失准角。受此启发，我们采用带反馈校正的卡尔曼滤波器来辅助大失准角初始对准。反馈校正是一种在动基座初始对准和组合导航中经常被采用的系统编排方式[8]，它是指在由卡尔曼滤波器得到系统误差的估计值后，将估计结果反馈回系统中，校正系统的力学编排方程。

在反馈校正时如果不加区分的反馈所有状态会由于某些状态的估计效果不佳而影响对准的精度。有学者提出通过可观测度给反馈状态加权决定其反馈程度可以改善反馈校正的效果[9]。因此，在大失准角初始对准中，我们只反馈校正我们希望迅速收敛的失准角ϕ和观测量δVn，而不反馈可观测性较差且对模型不确定性影响较小的状态εb和▽b。此外，反馈系数对系统输出也有一定的影响，反馈系数小系统输出会比较平滑，但是收敛时间较长，反馈系数大系统在初始阶段波动较剧烈，但是收敛较快，为了使大失准角迅速收敛这里选取反馈系数为最大值1。

2.2 P0阵的设置

标准卡尔曼滤波器的公式如式(7)所示：

当卡尔曼滤波器运行一段时间后，Pk-1矩阵将趋于一个小量，一般情况下R＞＞Q，由式(7)可以看出此时Pk/k-1＜＜R，Kk也趋近于一个小量，这将导致新息很难进入到估计结果中去，滤波估计对系统的修正变得微乎其微，如果这时系统还未收敛到小失准角，那么就很难再继续收敛了，将导致反馈校正失败。从这个角度来讲，P矩阵反映了反馈校正的动力，P越大反馈校正越充分。为了使反馈校正有效的将系统由大失准角“拉回”到小失准角，就必须提供足够大的P矩阵，一个最直接的办法是选用足够大的P0。考虑到系统12维状态的可观测性以及对反馈校正的贡献各不相同，需要进一步分析P0中各分量的设置。

δV是观测量，在滤波开始阶段主要依靠观测量来提供信息，所以P0中的δV应该设置的尽量大一些，当δV足够大时有即P1会迅速收敛到与P0无关的R水平，所以δV大了是没有坏处的。在滤波初始阶段ϕ的误差很大，主要依靠观测量来估计ϕ，所以P0中的ϕ也应设置为较大的值，同时为了避免随着滤波进行ϕ迅速变小，从而失去对大失准角反馈校正的“动力”，P0中的ϕ应设置的足够大。P0中的ε和▽不宜设置过大，过大会导致过分依赖量测来估计ε和▽，但是因为ε和▽不完全可观测，依靠量测估计出来的ε和▽是发散的，可能引起很大误差，同时ε和▽也不宜太小，太小会影响ε和▽中可观测分量的收敛速度。高精度陀螺和加表的常值零偏通常不大，ε和▽的初值设为零已经很接近真实值了，所以P0中的ε和▽可根据先验知识适当设置的小一些，例如（0.1～1）倍的经验值，▽的可观测性更弱一些所以可以设置的更小一些。综合考虑，推荐P0中的δV设置为10 m/s，ϕ设置为1000º，ε设置为先验知识的0.5倍，▽设置为先验知识的0.1倍。

2.3 强跟踪滤波器

仅仅依靠调节 P0阵来解决大失准角初始对准问题是不可靠的，有时候并不能将系统“拉回”到小失准角，这一点在后面的仿真中可以看到，因此需要一种能够在线调节P矩阵的方法，强跟踪滤波器（Strong Tracking Filter，STF）是一个很好的解决方案。强跟踪滤波器最早由周东华教授提出，强跟踪只是指它的性能，它实际上是一种自适应的指数渐消记忆卡尔曼滤波器。指数渐消是指通过引入渐消因子来使滤波器的记忆长度按照指数速度衰减，以提高对新近量测的利用程度。强跟踪滤波器通过新息正交原理来自适应的调节渐消因子，使得滤波器具有更强的关于模型不确定性的鲁棒性，更强的关于突变状态的跟踪能力，在故障检测、自适应控制等领域被广泛应用[10-11]。

早期使用的强跟踪滤波器中对所有的状态采用相同的渐消因子[12]，称之为单一渐消因子强跟踪滤波器（Single Fading Strong Tracking Filter，SFSTF）。仿真表明在初始对准中采用SFSTF会带来严重错误，究其原因在于并不是12个状态都存在严重“突变”，不同状态对模型不确定性的贡献差异巨大，因此必须对不同状态施加不同的渐消因子，这也是复杂多变量系统中经常采用的手段[13-14]。对不同变量采用不同渐消因子的强跟踪滤波器称为多重渐消因子强跟踪滤波器（Multiple Fading Strong Tracking Filter，MFSTF），MFSTF的公式与标准卡尔曼滤波器基本相同，只是在计算Pk/k-1时引入渐消因子矩阵，如式(8)所示：

Dk为渐消因子矩阵，是一个对角阵，对角元素是对不同状态分量施加的渐消因子。多重渐消因子的求解方法可以参考文献[14]，计算量并不大，而且当渐消因子取1时退化为标准卡尔曼滤波。此处，为了保证P矩阵的对称性，创新性的将式(8)改进为式(9)的形式，仿真显示这样做可以提高对准精度。

在 MFSTF中需要事先根据先验知识确定多重渐消因子的比例，考虑到大失准角初始对准中主要模型误差是失准角，因此确定渐消因子比例时突出对失准角的跟踪，选用

3 仿真验证

为了验证以上结论，进行了一系列仿真验证。仿真参数为：陀螺常值零偏0.01 (°)/h，角度随机游走系数0.001 (°)/√h，加表常值零偏100 μg，速度随机游走系数10 μg/√Hz；载体真实姿态[0°, 0°, 10°]，真实位置[40°, 116°, 50m]，真实速度0 m/s；卡尔曼滤波器状态初值X0=0，R=diag([0.01,0.01,0.01] m/s)2，Q根据陀螺角度随机游走系数和加表速度随机游走系数设置，P0= diag(k×[1°, 1°, 1°], [10, 10, 10] m/s, 0.5×[0.01, 0.01, 0.01] (°)/h, 0.1×[100, 100, 100] μg)2，其中k用于调节P0阵中ϕ的大小。

首先，验证了P0对大失准角初始对准的影响。仿真中采用带反馈校正的标准卡尔曼滤波器，初始姿态设为[1°, 1°, -170°]（对应航向角误差180°，是大失准角中最恶劣的情况），调节P0中的k从10-2～106变化，每次仿真时长3600 s，得到的航向角估计值如图1所示，图中红色虚线是真实航向角，黑色圆圈是仿真结果，右下角小图是局部放大图。由图 1可以看出 P0很小时得不到正确的航向估计，随着P0的增大，逐渐可以得到正确的航向估计，说明调节P0确实可以解决大失准角情况下的初始对准问题；当 P0设置为 100°以上时大多数情况下都可以得到正确的航向角，但是在约 390°时出现了一个“突变”，这说明并不是 P0越大，系统就一定能够收敛到正确的航向角，单靠调节P0的这种方法确实可靠性较差。

图1 P0对航向角估计的影响（KF）Fig.1 Effect of P0on the estimate of heading in KF

其次，验证了采用强跟踪滤波器对系统可靠性的提高。采用与前次仿真相同的参数，只是滤波算法由KF变为MFSTF，得到的航向角估计值如图2所示。对比图2和图1可以看出：采用MFSTF后，P0选用范围大大放宽了，选用任意值时都可以得到足够精确的航向估计，经过多次仿真也没有发现“突变”现象，说明采用强跟踪跟滤波器后大大提高了系统的可靠性，完美解决了大失准角初始对准问题。

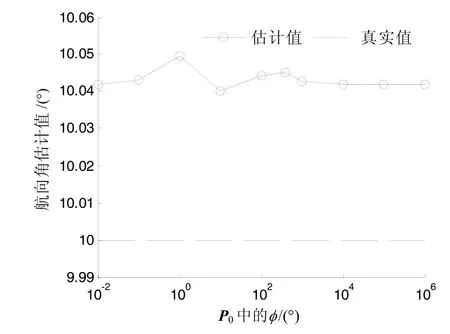
图2 P0对航向角估计的影响（MFSTF）Fig.2 Effect of P0on the estimate of heading in MFSTF

最后，综合比较了小失准角KF精对准方法、本文提出的 MFSTF方法和基于非线性模型的 UKF方法。仿真数据同前，KF方法中没有进行粗对准而直接将初始失准角设置为小角度（初始姿态[0.1°, 0.1°, 5°]），MFSTF和UKF的初始姿态都选为[1°, 1°, -170°]。三种方法的仿真结果如图3所示，图中的两幅小图是局部放大图。由图3可以看出MFSTF的收敛速度要明显快于 UKF，而且精度也比UKF高；MFSTF和KF几乎都在300 s左右收敛，速度和精度不相上下。

为了进一步比较三种算法的精度、速度和计算量，将一些有代表性的仿真结果列在表1中。从精度上看，零偏 0.01 (°)/h的陀螺对应的航向误差极限精度约为0.05°，比较300 s时的航向误差可以看出MFSTF和KF的都可以达到这个精度，而UKF由于尚未收敛而精度较差；从速度上看，KF和MFSTF都在300 s左右收敛到极限精度10.05°附近，收敛速度相差无几，而UKF在600 s时才收敛到10.5°附近，收敛速度远远慢于前两者；从计算量上看，比较各种算法处理3600 s数据的耗时可以看出 KF最短，MFSTF约是KF的1.1倍，而UKF约是KF的3.8倍，说明MFSTF的计算量与KF在同一水平，远小于UKF。通过以上比较可以看出，MFSTF可以很好地处理大失准角初始对准问题，与UKF相比精度、速度和计算量都有明显优势，与KF相比精度、速度和计算量均在同一水平，但省去了粗对准步骤，因而总耗时更少。

表1 KF、MFSTF和UKF比较Tab.1 Comparison among KF, MFSTF and UKF

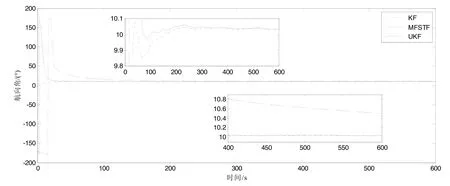
图3 KF、MFSTF和UKF航向角估计结果对比Fig.3 Comparison on heading estimates among KF, MFSTF and UKF

4 结 论

本文提出一种适用于静基座大失准角初始对准的新方法，无需进行粗对准，也无需采用非线性模型和非线性滤波，只须在传统的线性模型基础上选择合适的P0阵，并采用反馈校正滤波结构和强跟踪滤波器即可。仿真结果表明这种方法能够很好的解决大失准角初始对准问题，鲁棒性好，对准精度、收敛速度和计算量都明显优于基于非线性模型的UKF方法，与只适用于小失准角情况的标准卡尔曼滤波精对准方法在同一水平，但因无需粗对准而总耗时更短。这种新方法在大失准角初始对准领域非常实用。

（References）：

[1] Jiang Y F. Error analysis of analytic coarse alignment methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 334-337.

[2] 刘海鹏, 张科, 李恒年, 等. 捷联惯导系统大失准角下的初始对准研究[J]. 航空计算技术, 2012, 42(04): 39-42. Liu Hai-peng, Zhang Ke, Li Heng-nian, et al. Research on initial alignment of SINS with large misalignment angles[J]. Aeronautical Computing Technique, 2012, 42(4): 39-42.

[3] 龙瑞, 秦永元, 夏家和. CDKF在捷联惯导系统大失准角初始对准的应用[J]. 西北工业大学学报, 2010, 28(03): 364-368. Long Rui, Qin Yong-yuan, Xia Jia-he. Applying CDKF (Central Difference Kalman Filter) to initial alignment of sins for large misalignment angles[J]. Journal of Northwestern Polytechnical University, 2010, 28(3): 364-368.

[4] Jamshaid A, Rasheeq M. Initial orientation of inertial navigation system realized through nonlinear modeling and filtering[J]. Measurement, 2011, 44(5): 793-801.

[5] Wu Xu, Sun Feng. Simulation study for FOG strapdown inertial navigation nonlinear alignment based on SVD-cubature Kalman filter[C]//Symposium on Photonics and Optoelectronics. Shanghai, 2012: 1-4.

[6] 严恭敏, 严卫生, 徐德民. 基于欧拉平台误差角的SINS非线性误差模型研究[J]. 西北工业大学学报, 2009, 27(4): 511-516. Yan Gong-min, Yan Wei-sheng, Xu De-min. A SINS nonlinear error model reflecting better characteristics of SINS errors[J]. Journal of Northwestern Polytechnical University, 2009, 27(4): 511-516.

[7] 李汉舟, 潘泉, 邓麟, 等. 极点配置对SINS罗经对准性能影响[J]. 中国惯性技术学报, 2014, 22(06): 711-718. Li Han-zhou, Pan Quan, Deng Lin, et al. Pole assignment’s influence on alignment performance of SINS gyrocompass[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 711-718.

[8] Hu Jie, Cheng Xiang-hong. A new in-motion initial alignment for land-vehicle SINS/OD integrated system[C] //2014 Position, Location and Navigation Symposium. Monterey, CA, 2014: 407-412.

[9] 孙钰琛, 段凤阳, 陈鹏, 等. 基于可观测度分析的捷联惯导初始对准方法[J]. 压电与声光, 2014, 36(03): 380-383. Sun Yu-chen, Duan Feng-yang, Chen Peng, et al. Initial alignment method for SINS based on the analysis of the degree of observability[J]. Piezoelectrics & Acoustooptics, 2014, 36(03): 380-383.

[10] Wang L, Wu L, Guan Y, et al. Online sensor fault detection based on an improved strong tracking filter[J]. Sensors, 2015, 15(2): 4578-4591.

[11] Wang D, Zhou D H, Jin Y H, et al. Adaptive generic model control for a class of nonlinear time-varying processes with input time delay[J]. Journal of Process Control, 2004, 14(5): 517-531.

[12] Xia Qi-jun, Rao Ming, Ying Yi-qun, et al. Adaptive fading Kalman filter with an application[J]. Automatica, 1994, 30(8): 1333-1338.

[13] Gao Wei-xi, Miao Ling-juan, Ni Mao-lin. Multiple fading factors Kalman filter for SINS static alignment application[J]. Chinese Journal of Aeronautics, 2011, 24(4): 476-483.

[14] 赵小明, 赵帅, 郭永刚, 等. 基于强跟踪滤波的车载行进间对准[J]. 中国惯性技术学报, 2015, 23(2): 141-144. Zhao Xiao-ming, Zhao Shuai, Guo Yong-gang, et al. In-motion alignment based on strong tracking filter[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 141-144.

Strong tracking filter based SINS initial alignment for large misalignment angles

PENG Zhuo1,2, ZHANG Rong1, GUO Mei-feng1, LIU Gang1, LUO Shou-hong1
(1. Department of Precision Instrument, Tsinghua University, Beijing 100084, China; 2. Astronaut Center of China, Beijing 100094, China)

Initial alignment is important for strapdown inertial navigation system. Coarse alignment is usually implemented before fine alignment to make the misalignment angles sufficiently small to meet the linear error model. Without coarse alignment, the misalignment angles will be large enough to need non-linear model and non-linear filter, which are complicated and inaccurate. For this reason, a new method is presented which don’t need coarse alignment or non-linear model. This is achieved by choosing appropriate initial error covariance matrix and using feedback compensation structure and strong tracking filter. Simulation shows the new method is effective and robust for large misalignment angles. The heading error can ultimately converge to 0.05° after 300 s under arbitrary initial attitude, while the traditional fine alignment has almost the same accuracy and speed but needs additional time for coarse alignment, and the UKF only converges to 0.5° after 600 s which is much slower.

SINS; initial alignment; large misalignment angles; strong tracking filter

U666.1

：A

2015-05-07；

：2015-08-28

总装备部预研项目（20114113019）

彭卓（1986—），男，博士研究生，从事高精度惯性导航系统研究。E-mail：z-peng12@mails.tsinghua.edu.cn

联 系 人：张嵘（1969—），男，研究员，博士生导师。E-mail：rongzh@mail.tsinghua.edu.cn

1005-6734(2015)05-0565-05

10.13695/j.cnki.12-1222/o3.2015.05.002