光纤陀螺基于本征模态函数筛选的阈值滤波算法

肖文健，陈志斌，马东玺，张 勇，刘先红

（军械工程学院 军械技术研究所，石家庄 050000）

光纤陀螺基于本征模态函数筛选的阈值滤波算法

肖文健，陈志斌，马东玺，张 勇，刘先红

（军械工程学院 军械技术研究所，石家庄 050000）

为降低光纤陀螺随机噪声，提高其测量精度，利用周期图法辨识光纤陀螺的随机噪声特征参数，针对其噪声特征，提出了基于本征模态函数筛选的微分经验模态分解阈值滤波算法。以本征模态函数和原始信号二者的概率密度函数的空间距离为判别依据，对所有本征模态函数进行筛选，根据已估计的噪声参数计算阈值大小，采用时间序列阈值的方法对筛选出的本征模态函数进行处理。仿真和实验结果表明，该滤波算法能够在跟踪光纤陀螺信号变化的同时，使其零偏不稳定性下降90.35%，角随机游走下降93.75%，对随机噪声有较好的抑制能力。

光纤陀螺；随机噪声；微分经验模态分解；本征模态函数筛选

当前光纤陀螺（FOG）在航空航天等各个领域有着十分广泛和重要的应用，然而受内部结构和外界环境等因素的影响，在实际使用过程中其输出信号中往往伴有大量随机噪声。

光纤陀螺随机噪声的滤波方法主要分为建模滤波和非建模滤波。经典的建模滤波方法就是根据随机噪声时间序列建立ARMA模型，然后利用卡尔曼滤波实时更新该模型的输出[1-2]。这种建模滤波方法在随机噪声模型建立准确的情况下，具有较好的滤波效果，然而在实际应用中很难得到准确的随机噪声模型。非建模滤波则不需要建立误差模型。传统非建模滤波主要利用FIR、IIR等数字低通滤波器来滤除高频噪声，当信号和噪声的频带相近时效果较差。后来小波变换被应用到了光纤陀螺随机噪声的滤波中，小波变换具有良好的时频局部化特性[3]。然而小波分解与傅里叶分解类似，分解所用的基函数固定，不能自适应的跟踪信号变化。1998年Huang提出经验模态分解（EMD），该方法与传统信号分解方法的不同之处在于它不用选择基函数，而是据信号本身特征自适应地将信号分解成若干本征模态函数(IMF)[4]。传统EMD去噪方法需要分辨哪些IMF是信号哪些IMF是噪声，再进行信号重构。而实际中多数 IMF既含信号又含噪声，Kopsinis等人受小波阈值滤波的启发提出了EMD阈值滤波[5]，然而该方法只考虑了白噪声，没有分析有色噪声的滤波效果。Yu Gan等人指出惯性传感器的随机噪声是分形噪声，并通过改进阈值计算方法，使EMD阈值滤波在分形噪声滤波方面的得到应用[6]。在利用EMD滤波时，多数文献都是直接把EMD分解的第一个IMF分量当作噪声，然后对后面每个IMF分量分别进行阈值处理，而对IMF分量的筛选问题很少研究，这样不仅计算量大而且很难排除噪声干扰。

考虑到光纤陀螺信号与某些噪声频率相近，EMD分解出的IMF频率区段可能不会严格按照从高到低排列，产生波形混叠的现象。为了有效抑制光纤陀螺的随机噪声，本文在辨识光纤陀螺随机噪声特征基础上，提出一种基于IMF筛选的微分经验模态分解（DEMD）阈值滤波，在抑制噪声的同时，提高了DEMD阈值滤波算法的运行效率。

1 光纤陀螺随机噪声特征辨识

在 IEEE关于光纤陀螺测试标准中指出，光纤陀螺的随机噪声包括量化噪声、角随机游走、速率随机游走、零偏不稳定性和速率斜坡噪声[7]。这 5类噪声指标通常用来评价陀螺性能，而在实际对某一光纤陀螺的随机噪声进行滤波时，只需已知陀螺随机噪声表现出的总体噪声特征即可。根据当前国内外相关的研究，光纤陀螺随机噪声表现为分形噪声的特征。

分形噪声是白噪声的一般化，它的统计特征取决于只有一个参数 H（0＜H＜1）的二阶矩。分形噪声被定义为一个零均值稳定高斯过程，其自相关序列为[9]

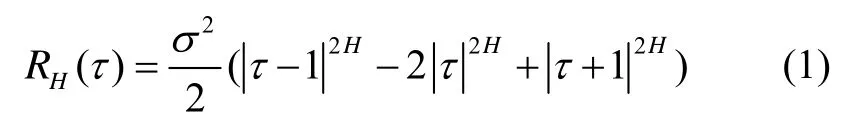
式中，τ为时延，σ2为RH(0)的方差。

辨识光纤陀螺随机噪声特性的主要任务就是计算参数H。目前参数H的估计方法有聚合序列方差法、R/S法、周期图法、Whittle法等[8]，根据光纤陀螺信号特征，本文选用周期图法。对于一个离散时间序列，将其自相关函数进行离散傅里叶变换，可以得到其功率谱密度函数为

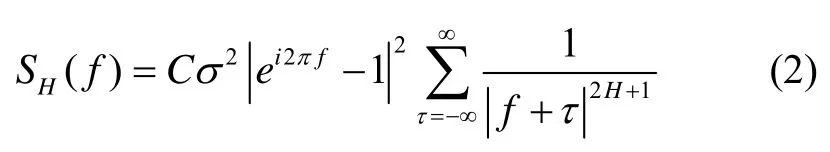
式中：f表示频率，C表示常数。其功率谱密度函数可以近似为

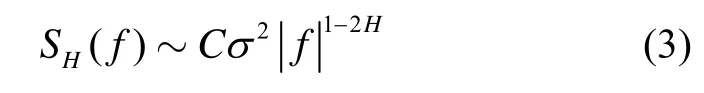
对公式(3)两边取对数可以得到：

本文选用的实验对象为俄罗斯Fizoptika公司生产的VG910型开环光纤陀螺，将其静置于隔振平台上采集其随机噪声并绘制周期图log- log曲线以及拟合直线如图1所示，其分形噪声参数H=0.879。

图1 光纤陀螺周期图log–log曲线及拟合直线Fig.1 Log–log periodogram and fitting line of FOG

2 光纤陀螺随机噪声滤波

2.1 DEMD滤波概述

对于传统EMD方法，若分解的信号频率比小于1.5或振幅比例小时，EMD 将不能区分两种成分，从而造成混波现象。DEMD能提高混合信号的振幅比，因而在一定程度上改善EMD中的混波现象[9]。信号通过DEMD分解流程如图2所示。

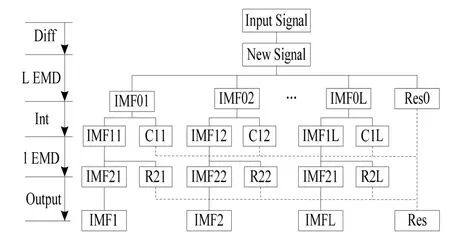
图2 DEMD分解流程图Fig.2 Flowchart of differential empirical mode decomposition

DEMD算法将原信号经过对时间一次求导，使新信号的能量尽可能地按频率从高到低递减，提高了对信号频率的分辨能力，这样就为DEMD在滤波方面的应用提供了可能。重构信号时，选取不同位置的IMF分量会产生不同的滤波效果，因此在DEMD滤波中，IMF筛选是非常关键的一个步骤。

2.2 IMF筛选准则

因为DEMD分解出的IMF分量从前到后频率逐渐减小，所以IMF分量按前后顺序可以分为只含噪声IMF、信号与噪声混合IMF以及只含信号IMF。目前在大多数文献中均把第一个或者前两个IMF分量直接当成纯噪声，然后再对后续的IMF分量进行相应处理。很显然，这种处理方法比较粗糙，不对所有IMF分量进行有效筛选，全部交由后续处理无疑会增加后续处理的工作量。所以采用DEMD滤波首先要对IMF分量进行筛选，找出信号与噪声混合 IMF同只含信号IMF分量的分界点m。这样对于前两个IMF分量当作噪声直接舍去，对于分界点m以后的IMF分量不做处理，只需要对中间处于3～m-1(m≥4)的IMF进行阈值处理，最后可按照公式(5)对信号进行重构。

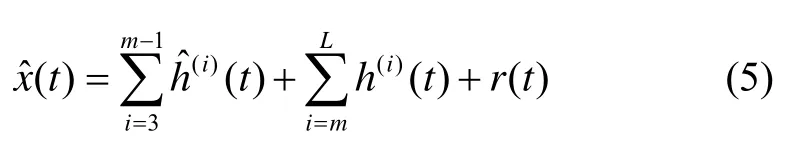
Ali Komaty等人从概率密度函数（PDF）的角度详细分析了每个IMF分量与信号之间的关系，并指出每个IMF分量PDF与原始信号PDF之间的相似度能够反映该IMF分量所含信号的比重[10]。受此启发，本文将IMF分量PDF与原始信号PDF之间的相似度用来作为 IMF筛选的标准。假设原始信号的 PDF为P( k)，某一IMF分量的PDF为Q( k)，那么它们的相似度定义为

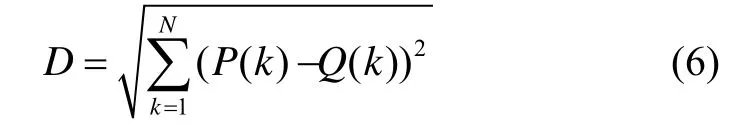
式中，N为滤波窗口内数据长度。分别计算每个IMF分量与原始信号的相似度即可得到每个 IMF分量与原始信号x( t)的相似度序列D( i), i=1～L。 D( i)序列中第一个局部极大值后开始减小的点即为要求取的分界点m，即：

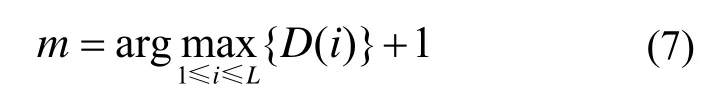
2.3 DEMD阈值滤波

在DEMD分解得到的IMF分量中，有一部分既包含噪声又包含信号。对于这一部分IMF分量，如果当作噪声直接舍去会丢失部分有用信息，如果当作信号直接采用则会引入部分噪声。对于这部分IMF分量可以对其进行阈值处理。

参照小波阈值滤波的思想，常用的阈值函数主要包括硬阈值函数和软阈值函数。本文通过实验发现，在对光纤陀螺随机噪声滤波过程中，使用软阈值滤波会丢失信号许多细节信息，与原始信号偏差较大，因此采用如下硬阈值函数：

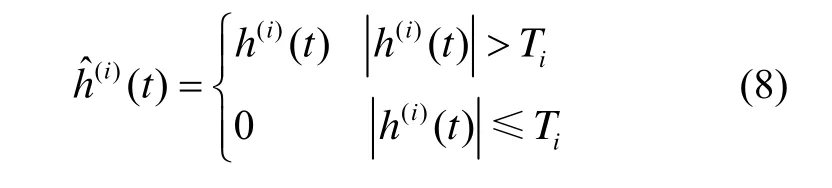
式中，Ti表示第i个IMF分量的阈值。

另外，对于每个IMF分量都有许多过零点，而且排位越靠前的过零点越多。考虑到每个过零点附近的IMF值比较小，低于设定的阈值，但这些数据也会包含有用信息，如果直接把低于阈值的数据置为零则会造成滤波后的信息部分缺失。因此本文采用区间阈值处理的方法来保护部分低于阈值的有用信息。对某一IMF分量，以相邻零点之间的时间序列为一个区间，若此区间内的极值大于阈值则保留，小于阈值则置零。如图3所示，左侧为原始信号，中间为采用直接硬阈值处理的结果，右侧为区间硬阈值处理的结果。从图 3中可以清楚地看出，采用时间序列区间硬阈值处理既能够较好地去除噪声干扰，又能较完整地保留有用信息。

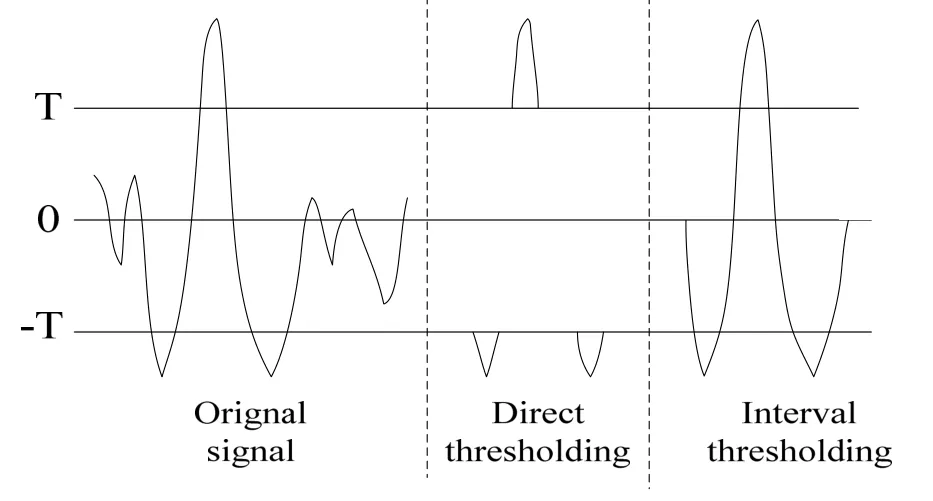
图3 直接阈值与时间序列区间阈值Fig.3 Direct thresholding and interval thresholding

对于每个IMF分量阈值的选择，比较经典的计算方法为

如前文所述，前两个IMF分量可认为只含噪声，所以其标准差为

由于后续IMF分量既包含噪声又包含信号，所以后续IMF分量的阈值不能直接用上式计算。参考文献[6]中给出了分形噪声经过EMD分解后每个IMF分量PSD之间的关系为

式中，k′＞k≥2，ρH近似满足

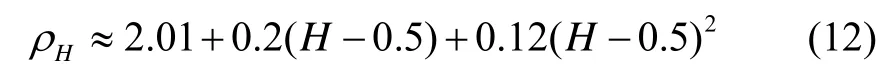
根据信号PSD与方差的关系，结合公式(12)可以得出：

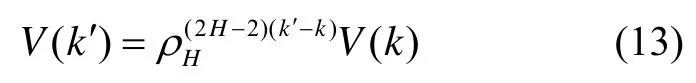
由式(13)即可计算后续IMF中包含噪声的方差为

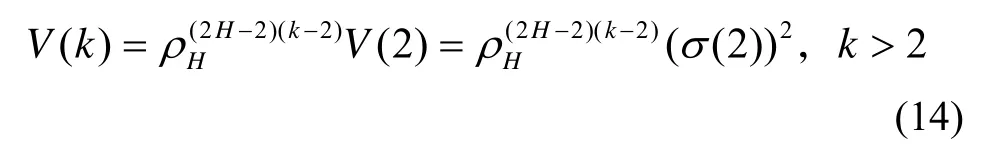
这样，利用公式(10)和公式(14)就可以得到整个IMF分量的阈值为

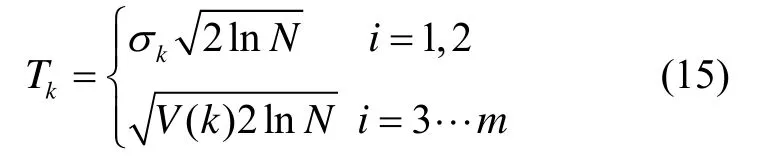
综上所述，本文提出的滤波算法具体过程为：

① 分析光纤陀螺随机噪声类型，利用周期图法确定分形噪声参数H；

② 对光纤陀螺原始信号进行DEMD分解，得到IMF分量；

③ 对所有IMF分量进行筛选，确定信号与噪声混合IMF同只含只含信号IMF的分界点m；

④ 计算每个IMF分量的噪声阈值；

⑤ 对位于3～m-1的 IMF进行时间序列区间的硬阈值处理得到

⑥ 利用公式(8)重构光纤陀螺输出信号。

3 实验与结果分析

为了验证本文所提出算法，分别进行了数据仿真实验和实际光纤陀螺滤波实验。

3.1 数据仿真实验

在Matlab软件中的标准测试信号中，Doppler信号是一种连续变化信号，频率覆盖范围大，相对其它测试信号更接近光纤陀螺实际信号，因此本文选用Doppler信号进行仿真。在Doppler信号基础上，分别加入3种不同参数的分形噪声以验证本文所提算法对不同参数噪声的适应能力。仿真所用分形噪声的具体参数为 H=0.2, 0.5, 0.8，所合成含噪信号的信噪比（SNR）均设定为5 dB。

以H=0.8的仿真过程为例对整个仿真过程进行说明。图4中粗实线表示Doppler标准信号，细虚线表示叠加了分形噪声的含噪信号。含噪信号经DEMD分解为9个IMF分量；然后利用本文提出的筛选准则对IMF分量进行筛选，确定临界点m=5；最后对含噪声IMF分量进行阈值滤波。为了说明该算法的滤波效果，这里将本文所述算法与小波阈值去噪以及传统基于EMD部分重构滤波进行了对比，如图 5所示。对于H=0.5和H=0.2时，使用同样步骤对信号进行滤波。分别计算在不同噪声参数下三种方法滤波后信号的均方根（RMS）误差，见表1。

分析仿真结果可以发现：

① 当 H=0.5时，小波阈值去噪方法与本文提出的方法滤波效果接近；当 H≠0.5时，小波阈值去噪方法的滤波效果降低，而本文提出的方法滤波效果基本不变。这是因为传统小波阈值对白噪声去噪效果较好，当噪声参数H=0.5时，信号的噪声为白噪声，所以此时滤波效果较好；而当H≠0.5时，信号的噪声为分形噪声，此时小波阈值去噪的效果则会下降。

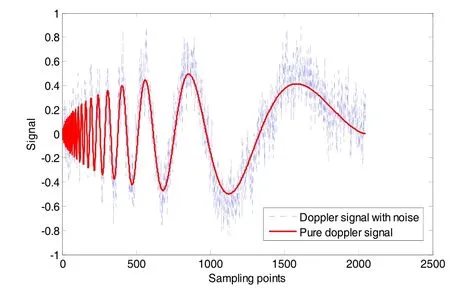
图4 标准Doppler信号与含噪Doppler信号Fig.4 Standard doppler signal and noised doppler signal

图5 三种方法滤波结果对比Fig.5 Filtering results of three denoising methods

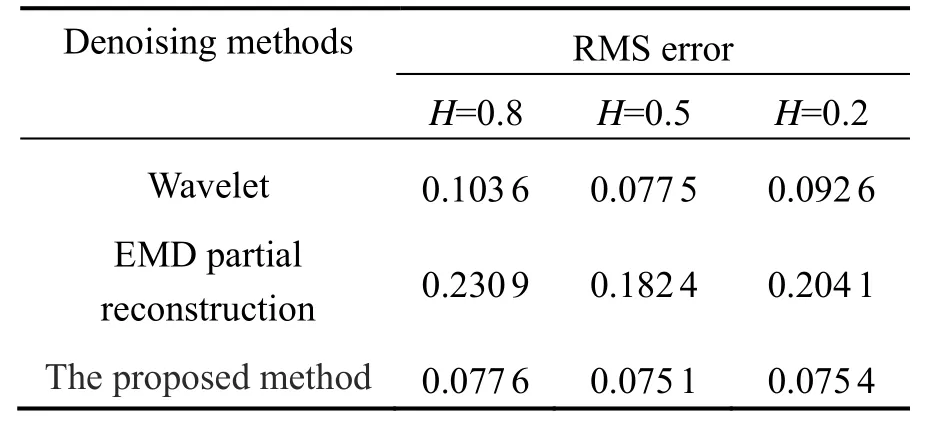
表1 三种方法滤波后信号的RMS误差Tab.1 RMS Errors of the signal after filtering

② 传统基于EMD的部分重构滤波效果受噪声参数变化的影响不大，但由于该方法在对信号进行重构时IMF仍带有部分随机噪声，所以该方法的滤波效果总体较差。

总体而言，仿真结果可以说明本文提出经过IMF筛选的DEMD阈值滤波效果较好，而且受噪声参数变化的影响很小。

3.2 光纤陀螺滤波实验

为了验证该滤波算法对光纤陀螺动态信号的跟踪与降噪能力，本文通过转台的摇摆运动向光纤陀螺输入动态信号。根据上文结果，实验所用光纤陀螺的分形噪声参数。对于光纤陀螺实际输出选用滑动窗口的方式滤波，滤波窗口N=500，滤波窗口的长度需综合考虑对滤波性能的要求，从而预先确定。设定摇摆运动的角位置满足，那么对其求导即可得到光纤陀螺的输入角速度实验中以100 Hz的采样频率采集10个摇摆周期的光纤陀螺输出数据。光纤陀螺的输出信号经DEMD分解为12个IMF分量；然后利用本文所述IMF筛选准则对其进行筛选，确定分界点m=8；再对筛选后的IMF进行阈值滤波处理，最终得到的滤波结果。光纤陀螺的信号原始信号与滤波后的信号如图6所示。

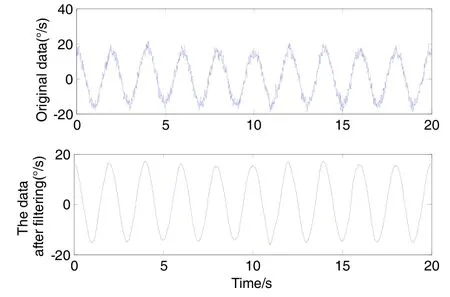
图6 滤波前后信号光纤陀螺信号Fig.6 FOG signal before and after filtering

为了定量的说明本文所述方法的滤波效果，分别计算滤波前后光纤陀螺信号 RMS误差以及用 Allan方差分析法获得滤波前后光纤陀螺的角随机游走和零偏不稳定性，如表2所示。

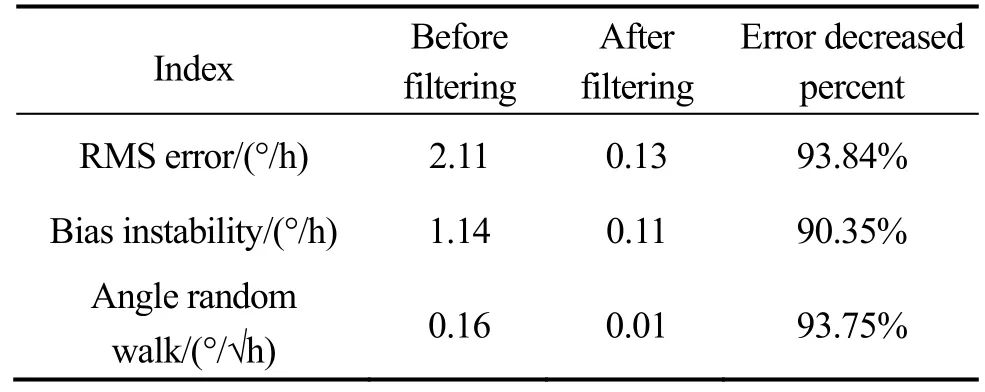
表2 光纤陀螺滤波前后噪声参数Tab.2 Noise parameters of FOG before and after filtering

从对光纤陀螺实际滤波的结果来看，本文所述算法在有效跟踪其信号变化的前提下，对其随机噪声具有较好的滤波效果。经过滤波后，该光纤陀螺的零偏不稳定性和角随机游走都有显著的下降，其中 RMS误差下降了 93.84%，零偏不稳定性下降了 90.35%，角随机游走下降了93.75%。

4 结 论

本文首先对光纤陀螺的噪声特征参数进行了辨识。针对其噪声特征提出了基于IMF筛选的DEMD时间序列阈值滤波算法。该算法首先以IMF和原始信号PDF的相似度为依据对IMF进行筛选，减少了IMF的处理个数；然后采用时间序列阈值处理的方法，对信号的噪声进行了有效滤除。采用滑动窗口的方法使得该算法能够在线运行。实验结果表明，本文所提出的算法相比传统的小波阈值去噪以及EMD部分重构去噪具有一定优势，在跟踪光纤陀螺信号变化的同时对于光纤陀螺的随机噪声具有良好的抑制能力。

（References）：

[1] Li Xue, Wang Qin. A novel Kalman filter for combining outputs of MEMS gyroscope array[J]. Measurement, 2012, 45(4): 745-754.

[2] 曾庆化, 黄磊, 刘建业, 等. 基于ARMA模型的光纤陀螺随机噪声滤波方法[J]. 中国惯性技术学报, 2015, 23 (1): 120-124. Zeng Qing-hua, Huang Lei, Liu Jian-ye, et al. Real-time filtering methods of FOG random noise based on ARMA model[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 120-124.

[3] 党淑雯, 田蔚风, 钱峰. 基于提升小波的光纤陀螺分形噪声滤除方法[J]. 中国激光, 2009, 36(3): 625-629. Dang Shu-wen, Tian Wei-feng, Qian Feng. De-noising fractional noise in fiber optic gyroscopes based on lifting wavelet[J]. Chinese Journal of Lasers, 2009, 36(3): 625-629.

[4] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proc. R. Soc. Lond. A, 1998, 454(3): 56-78.

[5] Kopsinis Y, McLaughlin S. Development of EMD-based denoising methods inspired by wavelet thresholding[J]. IEEE Transactions on Signal Process, 2009, 57(4): 1351-1362.

[6] Gan Yu, Sui Li-fen, Wu Jiang-fei, et al. An EMD threshold de-noising method for inertial sensors[J]. Measurement, 2014, 49: 34-41.

[7] IEEE Std 952-1997. IEEE standard speciation format guide and test procedure for single-axis interferometric fiber optic gyros[S]. New York: IEEE Standards Board, 1997.

[8] 韩忠明, 赵庆展, 李伟. Hurst参数估计方法的性能评价与分析[J]. 计算机应用与软件, 2010, 27(9): 56-58. Han Zhong-ming, Zhao Qing-zhan, Li Wei. Performance evaluation and analysis of Hurst parameter estimate methods[J]. Computer Applications and Software, 2010, 27(9): 56-58.

[9] Li Ming, Li Fu-cai, Jing Bei-bei, et al. Multi-fault diagnosis of rotor system based on differential-based empirical mode decomposition[J]. Journal of Vibration and Control, 2013, 20(3): 1-17.

[10] Komaty A, Boudraa A O, Augier B, et al. EMD-based filtering using similarity measure between probability density functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27-34.

De-noising method of FOG with DEMD threshold based on IMF criterion

XIAO Wen-jian, CHEN Zhi-bin, MA Dong-xi, ZHANG Yong, LIU Xian-hong
(Ordnance Technology Institute, Ordnance Engineering College, Shijiazhuang 050000, China)

To reduce the random noise of fiber optic gyro (FOG) and improve its measurement precision, the characteristic parameters of FOG random noise are identified by the method of periodogram. According to the noise characteristics, a de-noising method with differential empirical mode decomposition (DEMD) interval thresholding is proposed based on intrinsic mode function (IMF) criterion. The relevant IMFs are selected based on the space distance of the probability density functions (PDF) between the original signal and each IMF. The filtering thresholdings are calculated by the estimated noise parameters, and the relevant IMFs are filtered by the DEMD interval thresholding. Simulation and test results show that the FOG’s bias instability is decreased by 90.35% and the FOG’s angle random walk is decreased by 93.75% after filtering by the proposed method.

FOG; random noise; differential empirical mode decomposition; intrinsic mode functions criterion

V249.3

：A

2015-06-05；

：2015-09-21

国家自然科学基金（51308075）

肖文健（1989—），男，博士研究生，从事光电测量与信号处理研究。E-mail：xiao_wen_jian@163.com

联 系 人：陈志斌（1965—），男，研究员，博士生导师。E-mail：shangxinboy@163.com

1005-6734(2015)05-0685-05

10.13695/j.cnki.12-1222/o3.2015.05.022