基于迭代计算的地磁轮廓线匹配算法

解伟男，李清华，奚伯齐，黄黎平，王常虹

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

基于迭代计算的地磁轮廓线匹配算法

解伟男，李清华，奚伯齐，黄黎平，王常虹

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

针对惯性/地磁匹配组合导航系统，提出了一种基于迭代计算的地磁轮廓线匹配新算法，可以有效地修正惯导系统的初始位置误差和初始航向误差，并具有较高的实时性。首先以均方差准则建立匹配轨迹和实测地磁特征量的相关性约束，引入匹配曲线的参数化模型，通过泰勒展开并忽略高阶小项，将相关性约束简化为曲线平移位移和航向误差角的多变量表达式。然后依据相关性准则，将地磁匹配问题转化为以曲线平移位移和航向误差角为变量的非线性方程组的求解问题。采用牛顿迭代求解非线性方程组，实现地磁轮廓线匹配。最后仿真结果表明，基于迭代计算的地磁轮廓线匹配方法的最大匹配误差为传统轮廓线匹配方法的18.2%，为等值线约束迭代最近点匹配方法的7.8%，并且所提出的新方法耗时仅为5 ms，满足实时匹配要求。

地磁匹配；轮廓线匹配；迭代；均方差准则

地磁匹配导航以地球的基本物理场为基础，通过线图匹配实现导航定位，具有无源、无辐射、隐蔽性强、误差不随时间累积等众多优点，因此作为近年来新生的辅助惯性导航的手段，在确保武器系统导航信息的安全性、可靠性和自主性方面展现出了巨大的军事潜力[1-3]。

目前，地磁匹配算法主要分为两大类：第一类是轮廓线匹配算法，该算法具有原理简单，适用范围广，对初始误差要求低等优点。然而该方法要求根据惯导系统输出的参考轨迹形状，遍历有效范围内所有平行于参考轨迹的序列，并通过相关性准则确定最优的匹配结果，算法的实时性受到搜索范围和搜索步长的制约，而且该算法无法修正惯导系统的初始航向误差，匹配精度较差[4-5]。第二类是ICCP匹配算法，ICCP匹配算法最初由图像配准算法ICP（Iterative Closest Point）发展而来[6]，ICCP匹配算法求取测量轨迹与最近等值点轨迹之间的最优刚性变换，通过该变换校正测量轨迹来实现匹配的目的，ICCP匹配可以同时修正惯导系统的初始位置误差和初始航向误差。然而该算法以磁场测量等值线上的最近点序列作为匹配目标，因此算法收敛于该最近点序列而不收敛于真实轨迹序列，因此算法精度无法得到保证；此外ICCP算法在寻找最近点时需要耗费较多时间，这也影响了算法的实时性[7-8]。也有学者针对上述问题进行改进，比如将两类匹配算法融合[9]以及采用仿生学匹配算法[10-11]等，然而匹配算法的精度、实时性等问题还有待进一步研究。

本文提出了一种基于迭代计算的地磁轮廓线匹配新算法。该算法引入匹配曲线的参数化模型，并通过泰勒展开将 MSD相关性约束转化为曲线平移位移和航向误差角的多变量表达式，从而将匹配问题转化为非线性方程组的求解问题，最终通过迭代计算实现地磁匹配。该算法可以有效地消除惯导系统的初始位置误差和初始航向误差，并具有较高的实时性。

1 迭代匹配原理

1.1 问题描述

如图1所示的地磁匹配示意图。曲线Rf为惯导系统输出的轨迹曲线，即参考轨迹；曲线M为匹配算法求得的匹配轨迹曲线，即匹配轨迹，其位于真实轨迹曲线附近；曲线Rf ′与匹配轨迹平行，参考轨迹与匹配轨迹之间的夹角为α，即航向误差角。从图中可以看出参考轨迹与匹配轨迹间存在着平移和旋转，对应着惯导系统的初始位置误差和初始航向误差。令点(a, b)T为参考轨迹上的任意一点，其对应的匹配轨迹点为(u, v)T，其中(a, u)表示点的经度，(b, v)表示点的纬度。

图1 地磁匹配示意图Fig.1 Illustration of geomagnetic matching

1.2 性能指标

分别用I( a, b)、I( u, v)表示点(a, b)T和点(u, v)T所在位置对应的地磁图库中地磁场特征值。考虑到参考轨迹在匹配轨迹附近，即可将I( u, v)泰勒展开：

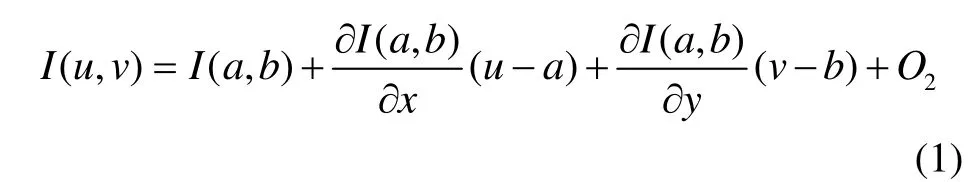
式中，∂I( a, b)/∂x表示地磁特征值对经度方向的梯度在点(a, b)T上的取值，∂I( a, b)/∂y 表示地磁特征值对纬度方向的梯度在点(a, b)T上的取值，O2为高阶小项。

采用均方差准则计算曲线的相关性，即计算匹配轨迹曲线上各点所对应的地球磁场特征值与真实磁场测量值之差的平方和的均值，如式(2)所示：

式中，Ir(a, b)为载体在参考点(a, b)T时磁传感器实时测量得到的地磁特征值，L为参考曲线的长度。

将泰勒展开式(1)带入式(2)，并忽略高阶小项O2，可以得到如式(3)的相关性约束：

在不引起混淆的情况下，可将相关性约束(3)写成如下简化形式：

这里存在u和v两组位置变量而只有一个约束，显然不能唯一的确定匹配结果。传统的轮廓线匹配方法是遍历所有平行于参考轨迹的曲线，使相关性约束(4)取最小值的曲线即为所求。首先这种方法的实时性受到搜索范围和搜索步长的制约，匹配速度慢；其次，该方法只能修正惯导系统的初始位置误差，匹配精度差。若加入航向等误差进行搜索，计算量会大幅度升高，难以在线计算。

本文将建立匹配轨迹的参数化模型，并将该模型引入相关性约束，从而将遍历搜索方法转化为快速迭代算法。设参考轨迹Rf的描述方程为

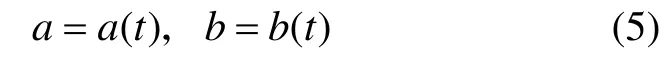
式中，t为参考轨迹的参变量。

如图1所示，当惯导系统存在初始位置误差和初始航向误差时，匹配曲线M的描述方程为

将参考轨迹Rf离散化成n( n＞2)个点，其对应离散点的坐标为可以得到离散化的均方差约束指标函数：

因此地磁匹配问题可以转化为寻求Δx、Δy和α，使指标函数(8)取极小值。

1.3 匹配求解

为使指标函数(8)取极小值，可分别将指标函数对自变量Δx、Δy和α求一阶偏导数，并令其为零，即

将均方差约束指标函数(8)带入式(9)可得：

因此地磁匹配可以转化为由Δx、Δy和α组成的非线性方程组(13)的求解问题，该非线性方程组可通过Newton迭代法求解。匹配结果可以通过式(6)计算得到。

2 迭代匹配算法

基于迭代计算的地磁轮廓线匹配算法的实现步骤如下：

第二步：根据参考轨迹离散化的n个位置，从预先存储的地磁数据库中读取该位置的地磁特征值并根据地磁数据库信息计算该位置的地磁特征值梯度信息

第三步：初始化迭代变量

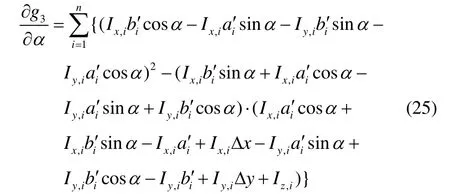
第五步：求解线性方程组

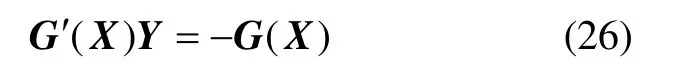
第六步：更新迭代变量

第七步：判断是否满足终止迭代条件，若满足则停止迭代并跳到第八步，否则跳到第四步。

终止迭代的条件有两个，满足任意一个即终止迭代：① 迭代次数达到预设的最大迭代次数；② 迭代变量增量Y的2范数小于设定值，即

式中，ε＞0为预先给定的迭代最小误差。第八步：根据迭代变量计算匹配结果

根据上述匹配步骤可知，迭代计算过程中地磁特征值梯度信息Ix,i和Iy,i并不改变，因此可以将匹配区域地磁特征值梯度信息事先存入载体计算机中，匹配计算前直接在载体计算机中检索得到，也可以通过检索载体计算机中的地磁特征值信息后计算得到。

需要指出的是，基于迭代计算的地磁轮廓线匹配算法假设参考轨迹位于匹配轨迹附近，在忽略高阶小项O2的基础上，以一阶差分的形式近似相关性约束。然而当惯导系统的初始误差较大时，忽略的高阶小项O2会严重影响算法的精度。为了克服上述问题，可以采用多次迭代的方式提高匹配算法的精度。在多次迭代时，可以将当前的迭代结果作为下一次迭代的参考轨迹。

3 仿真实验

为了考察上述算法的有效性，本节对算法进行仿真验证。根据地球磁场异常网格(EMAG2)绘制中国东北某位置的地磁异常图作为匹配背景磁图，仿真过程中，选取地磁匹配区域内的某条直线航迹作为真实轨迹，对真实航迹叠加一定的旋转和平移误差作为惯导系统输出的参考轨迹，如图2所示，其中初始位置误差为(0.04°, -0.04°)，初始航向误差为0.8°。

仿真时首先假设磁传感器没有测量噪声，图3和图4分别给出了经度误差曲线和纬度误差曲线，其中算法1为传统的轮廓匹配算法[4]，算法2为ICCP匹配算法[7]，算法 3为基于迭代计算的地磁轮廓线匹配算法，算法4为采用二次迭代的基于迭代计算的地磁轮廓线匹配算法。仿真结果表明，所提出算法的最大误差为传统轮廓线匹配最大误差的11.0%，为ICCP匹配最大误差的3.6%。

图2 真实轨迹和参考轨迹Fig.2 The real track and the reference track

若在地磁数据中加入幅值为2 nT的随机噪声，匹配结果如图5和图6所示。仿真结果表明，所提出算法的最大误差为传统轮廓线匹配最大误差的 18.2%，为ICCP匹配最大误差的7.8%。

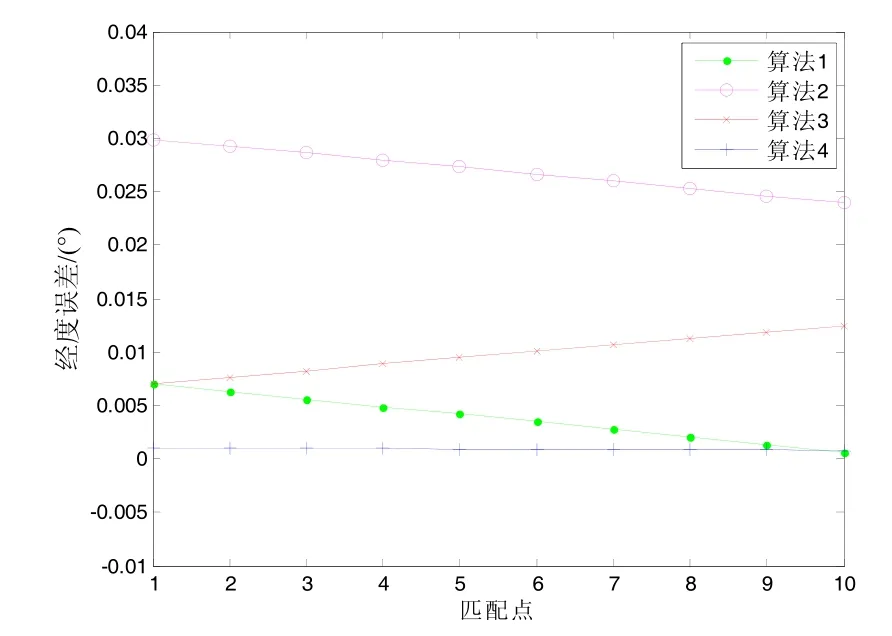
图3 忽略传感器噪声时匹配经度误差曲线Fig.3 Longitude errors of matching results without the magnetic sensor noise

图4 忽略传感器噪声时匹配纬度误差曲线Fig.4 Latitude errors of matching results without the magnetic sensor noise

根据匹配结果可以看出，基于迭代计算的地磁轮廓线匹配算法具有较高的匹配精度，可以修正惯导系统的初始位置误差和初始航向误差。此外，若采用多次迭代，匹配精度可以进一步提高。

利用Matlab中的tic和toc语句计算匹配算法运行时间，传统的轮廓线匹配算法在仿真计算机中总耗时为6.1 s（搜索步长为0.001°）；ICCP匹配算法在仿真计算机中总耗时为1.4 s；采用二次迭代的基于迭代计算的地磁轮廓线匹配算法在仿真计算机中总耗时约为5 ms。因此所提出的算法具有较高的实时性，可以保证地磁导航的在线计算。

图5 考虑噪声时匹配经度误差曲线Fig.5 Longitude errors of matching results with random noise

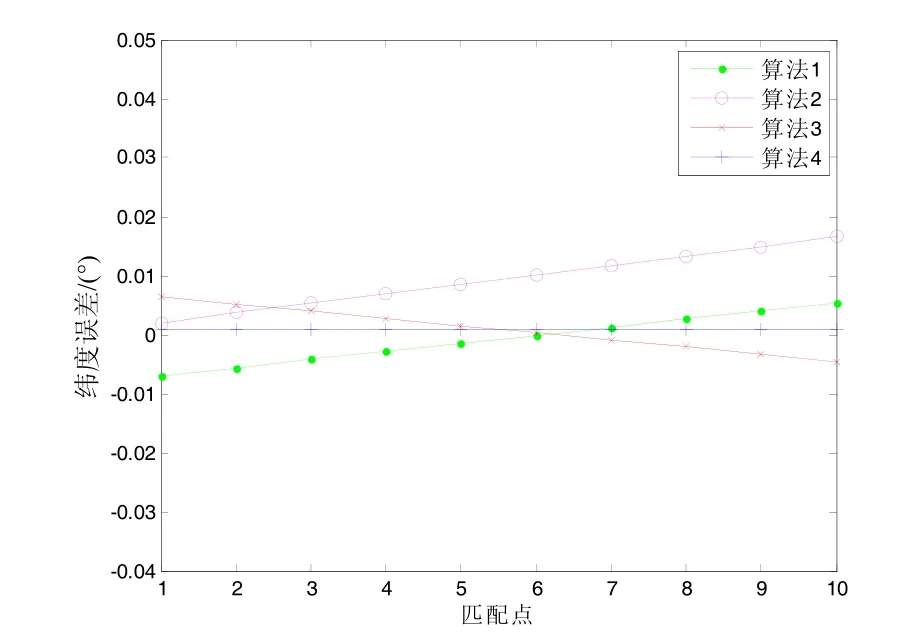
图6 考虑噪声时匹配纬度误差曲线Fig.6 Latitude errors of matching results with random noise

4 结 论

本文提出了一种基于迭代计算的地磁轮廓线匹配新方法。该方法将匹配问题转化为以匹配曲线参数为变量的非线性方程组，通过迭代计算求解非线性方程组从而确定匹配结果。仿真结果表明，所提出算法的最大匹配误差为传统轮廓线匹配最大误差的 18.2%，为ICCP匹配最大误差的7.8%。此外，所提出的算法在仿真计算机中的总耗时约为5 ms。因此提出的基于迭代计算的地磁轮廓线匹配算法可以有效的提高匹配导航的定位精度，改善匹配导航的实时性。

（References）：

[1] Batista P, Petit N, Silvestre C, Oliveira P. Further results on the observability in magneto-inertial navigation[C]// 2013 American Control Conference. 2013: 2503-2508.

[2] Wang Peng, Wu Yuan-xin, Hu Xiao-ping, Ruan Qing. Geomagnetic aided navigation suitability evaluation based on principal component analysis[C]//2012 International Conference on Industrial Control and Electronics Engineering. 2012: 324-329.

[3] Guo Cai-fa, Cai Hong, G H M van der Heijden. Feature extraction and geomagnetic matching[J]. The Journal of Navigation, 2013, 66(6): 799-811.

[4] 陈励华, 王仕成, 孙渊, 等. 地磁缓变区域的多维特征量匹配方法[J]. 中国惯性技术学报, 2011, 19(6): 720-724. Chen Li-hua, Wang Shi-cheng, Sun Yuan, et al. Matching of multi-dimensional feature elements in areas with smooth magnetic fields[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 720-724.

[5] Xie Wei-nan, Qu Zhen-shen, Li Qing-hua. A fast algorithm of the geomagnetic correlation matching based on MSD[C]//The 3rd International Conference on Control, Automation and Systems Engineering. 2013: 59-62.

[6] Besl P J, Mckay N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[7] 康崇, 张晓峻, 樊黎明. 基于 ICCP算法的地磁匹配辅助导航[J]. 应用基础与工程科学学报, 2014, 22(3): 598-605. Kang Chong, Zhang Xiao-jun, Fan Li-ming. Geomagnetic-matching aided navigation based on ICCP algorithm [J]. Journal of Basic Science and Engineering, 2014, 22(3): 598-605.

[8] Zhang Yan-shun, Li Chun-yu, Liu Shan-shan, Jiang Ming, Guo Lei. Locating method of geomagnetic/inertial integrated navigation system by forecasting the geomagnetic matching initial value[C]//2014 IEEE Chinese Guidance, Navigation and Control Conference. 2014: 235-239.

[9] 王胜平, 张红梅, 赵建虎, 等. 利用TERCOM与ICCP进行联合地磁匹配导航[J]. 武汉大学学报(信息科学版), 2011, 36(10): 1209-1212. Wang Sheng-ping, Zhang Hong-mei, Zhao Jian-hu, et al. Marine geomagnetic navigation technology based on Integration of TERCOM and ICCP[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1209-1212.

[10] 王跃钢, 贾磊, 单斌, 等. 自适应SA-ACO地磁匹配导航算法[J]. 中国惯性技术学报, 2014, 22(1): 89-93. Wang Yue-gang, Jia Lei, Shan Bin, et al. Adaptive SA-ACO geomagnetic matching navigation algorithm[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 89-93.

[11] Liu Ming-yong, Li Hong, Liu Kun. Geomagnetic navigation of AUV without a priori magnetic map[C]//2014 OCEANS. 2014: 1-5.

Geomagnetic contour matching algorithm based on iterative method

XIE Wei-nan, LI Qing-hua, XI Bo-qi, HUANG Li-ping, WANG Chang-hong
(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China)

A novel geomagnetic contour matching algorithm based on iterative method is proposed for inertial/geomagnetic integrated navigation systems, which can correct the initial position and heading errors of INS (Inertial Navigation Systems), and lead to high real-time performance. First, the correlation constraint of the matching track and geomagnetic characteristic value is built according to MSD (Mean Square Deviation) criterion. By introducing the parameterized model of the matching track and neglecting the higher-order expanded terms of the first order Taylor expansion, the correlation constraint is translated into a mathematical expression of the displacement and initial heading error. Then the geomagnetic matching problem is converted to the solutions of nonlinear equations according to the correlation criterion. Newton iteration is applied to implement the geomagnetic matching algorithm. Simulation results indicate that the matching error of the contour matching algorithm based on iterative method is decreased to 18.2% compared to conventional contour matching method, and is decreased to 7.8% compared to ICCP (Iterated Closest Contour Point) matching method. Meanwhile, the time consumed in the proposed algorithm is only 5 ms, meeting the real-time requirement.

geomagnetic matching; contour matching; iteration; mean square deviation

V249.3

：A

2015-05-15；

：2015-09-21

国家自然科学基金（61403095，61375046）；总装预研项目（51309040401）

解伟男（1979—），男，讲师，从事地磁导航技术研究。E-mail：xieweinan@hit.edu.cn

联 系 人：李清华（1979—），男，副研究员。E-mail：huahit@hit.edu.cn

1005-6734(2015)05-0631-05

10.13695/j.cnki.12-1222/o3.2015.05.013