伪距/伪距率/双差分载波相位组合导航方法

李 安，冯卡力，覃方君

（1. 海军工程大学 训练部，武汉 430033；2. 海军工程大学 电气工程学院，武汉 430033）

伪距/伪距率/双差分载波相位组合导航方法

李 安1，冯卡力2，覃方君2

（1. 海军工程大学 训练部，武汉 430033；2. 海军工程大学 电气工程学院，武汉 430033）

为了提高组合导航的精度，提出了一种伪距/伪距率/双差分载波相位组合导航方法。通过构造双差分载波相位观测量，以消除组合导航中若干误差源，避免整周模糊度的求解。为了避免组合后误差积累发散，引入伪距/伪距率信息，设计了一种新的滤波器。该滤波器能发挥载波相位高精度和伪距/伪距率包含绝对信息的优势。最后利用 GPS实测数据和仿真惯性导航数据进行组合导航试验。试验中对比了伪距组合、双差分载波相位组合等常见组合导航方法。两小时试验结果表明，提出的组合导航方法比传统伪距组合方法的平均水平定位精度高61.13%，方法可行。

组合导航；捷联惯导；双差分载波相位；伪距；伪距率

紧组合利用的是GPS的原始观测量，通常使用测码伪距观测量和测相伪距观测量，即伪距和载波相位观测量[1-2]。此方法不需要 GPS基站的辅助，并且只要可以观测到卫星（无数目限制，最少一个），便可获得组合定位的结果，抗干扰性较好。

利用载波相位进行组合时，首先需要进行整周模糊度的解算，根据文献[5]的研究，整周模糊度的收敛时间一般为30 min左右。在使用过程中若GPS信号因干扰等原因而丢失，需重新解算整周模糊度[6-7]。因此该方法不能满足实时性和无区域限制要求。国内外学者对伪距和载波相位做了大量研究。根据文献[8]，Wendel J和Trommer G F等人对连续的载波相位进行差分操作，消除了整周模糊度问题，但是保留了接收机钟差。文献[9]将差分后的载波相位与伪距组合，取得了较好组合效果。本文在此基础上，对差分后的载波相位作进一步消除钟差处理，并将伪距率的信息引入到组合中，提出基于伪距/伪距率/双差分载波相位的组合导航方法。试验表明该方法满足高精度、无区域限制、实时性导航的要求。

1 基本思路

为了避免整周模糊度解算，本文构造了一种新的双差分载波相位观测量。首先将连续的载波相位作差分处理，该操作可消除载波相位的整周模糊度、电离层误差、对流层误差、卫星轨道误差、多径效应和卫星钟差。然后再选取一颗可观测卫星作为基准星，将差分后的载波相位和来自基准星的差分后的载波相位观测量进行二次差分，可得到不含接收机钟差的观测量。由于双差分载波相位是经过两次差分运算得到的，其在本质上反映的是接收机位置的增量，因而不含绝对位置信息。当它与惯导进行组合时，由于没有绝对位置信息的校正，导致组合结果中存在缓慢的位置误差积累。伪距和惯导的组合中包含有绝对的位置信息，系统具有很好的可靠性和实时性[10]。引入伪距率信息后，增加了系统的可观测性，对于速度估计更加准确，并且伪距率是经过微分得到，在载体动态性较强时，比伪距具有更好的适应性[11]。综合考虑将伪距、伪距率、双差分载波相位与捷联惯导进行组合。

2 伪距/伪距率/双差分载波相位组合导航方法

2.1 状态方程

根据捷连惯导输出数据的特点，选择当地地理坐标系为导航坐标系。由于差分操作已经消除了星差和钟差，所以选取惯导的15个误差量作为状态变量，即根据惯导的误差方程，导航系下组合导航系统的状态方程为[12]

2.2 双差分载波相位观测方程

设接收机和卫星间的几何距离为 ri，则载波相位的观测方程如[13]下：

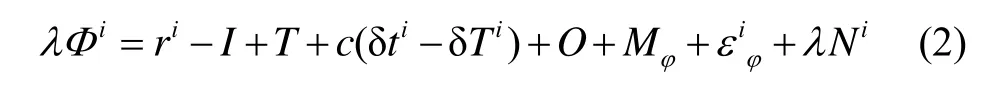
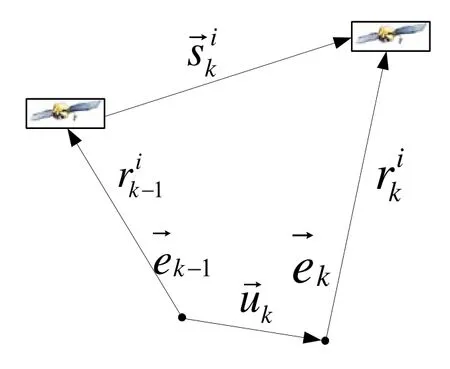
图1 相邻历元卫星和接收机关系Fig.1 Positions of satellite and GPS antenna for two successive epochs

在相邻两个卫星历元之间求差分，由于I、T、O、Mφ具有很强的空间、时间相关性，并且δTi的变化可忽略，因此可得差分后的方程为

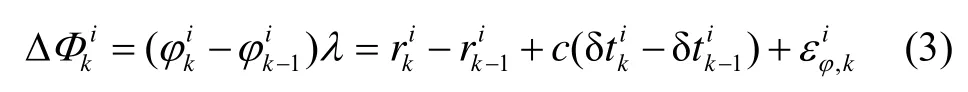
根据几何关系和向量的知识可得：

带入式(3)中，可得：

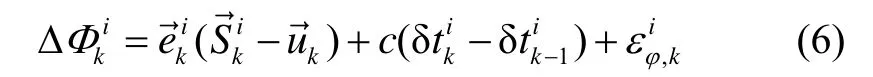
并考虑到

为消除接收机钟差，再找一颗卫星作为参考星，对观测到的载波相位进行上述运算后，将两者的结果再作差，得到不含钟差的观测量，命名为双差分载波相位。

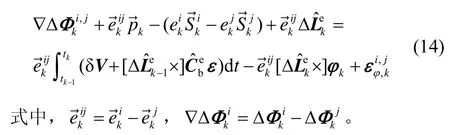
设观测方程形如：

则式(15)即为双差分载波相位观测方程，其中，V(k)为量测噪声。

3 试验验证

本文方法主要利用双差分载波相位高精度，伪距/伪距率提供绝对位置信息对滤波后误差发散进行抑制。为验证其效果，利用GPS实测数据和仿真惯性导航数据，进行了组合试验。选用传统的伪距组合、双差分载波相位组合两种组合方法对同一组数据进行组合，将得到的结果与本文方法相比较，组合效果见下图。试验中，陀螺漂移为0.01 (°)/h，加表零偏为 1×10-5g。

图2为伪距组合对比试验曲线；图3为双差分载波相位组合对比试验曲线，图 4为本文提出的伪距/伪距率/双差分载波相位组合。

对比图2、图3和图4可以发现，采用惯导与本文定义的双差分载波相位观测量进行组合，其效果远优于传统的伪距组合，滤波后误差收敛更快，收敛效果更好。但采用双差分载波相位组合后，误差存在缓慢的积累发散效应，计算发现，在2 h后水平位置误差发散达到13 m，高度误差发散达到12 m。可以预见，随着导航时间的推移，滤波后误差会不断增大。图4由于采用本文方法，组合后误差略大于短期内双差分载波相位组合后误差，但长时间来看，伪距包含的绝对位置信息有效地抑制了图 3中出现的发散现象，验证了本文提出的组合方法同时具有高精度、长时间有效两个优势。

为更加直观具体的展示上图中的组合效果，选取伪距、双差分载波相位和本文方法组合后的位置误差进行比较，结果见表1，位置误差单位为m。

表1清晰地表明，双差分载波相位组合短期内具有非常高的精度，组合效果优于其它方法，但由于存在误差积累效应，在3000 s后，误差发散到5 m，2 h后误差已经达到13 m。而本文方法因为存在位置信息校正，不存在发散现象，组合效果略优于双差分载波相位组合方法，明显优于伪距组合方法。

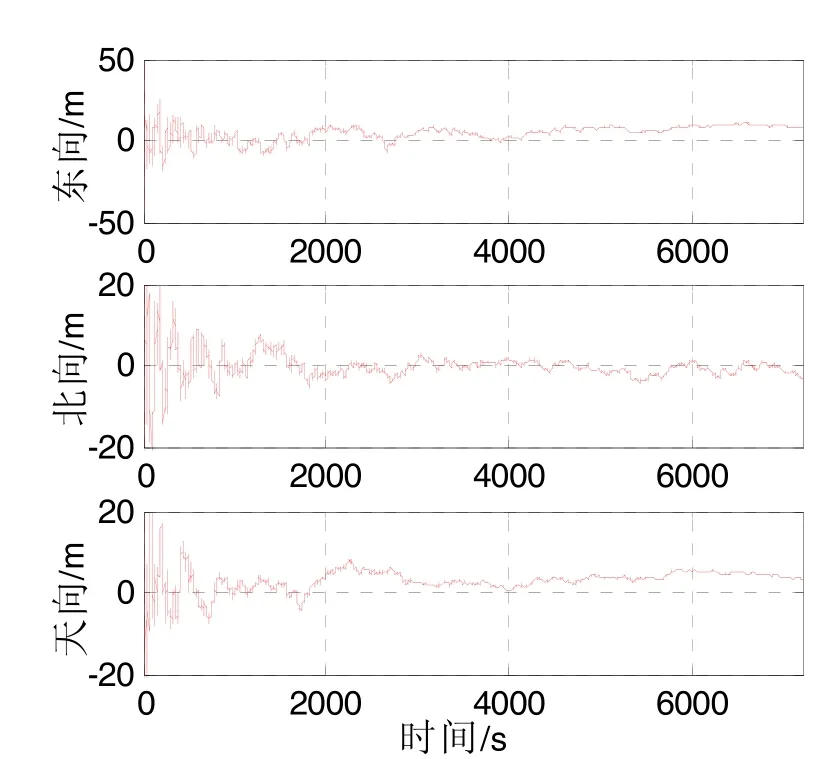
图2(a) 位置误差Fig.2(a) Position error

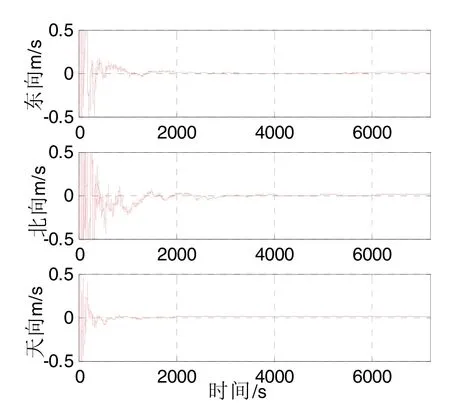
图2(b) 速度误差Fig.2(b) Velocity error

图3(a) 位置误差Fig.3(a) Position error

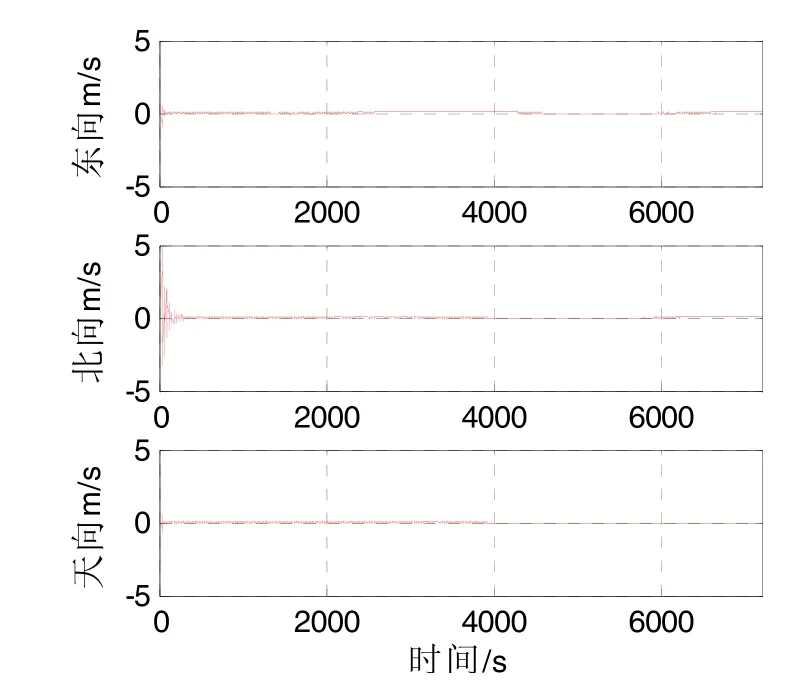
图3(b) 速度误差Fig.3(b) Velocity error

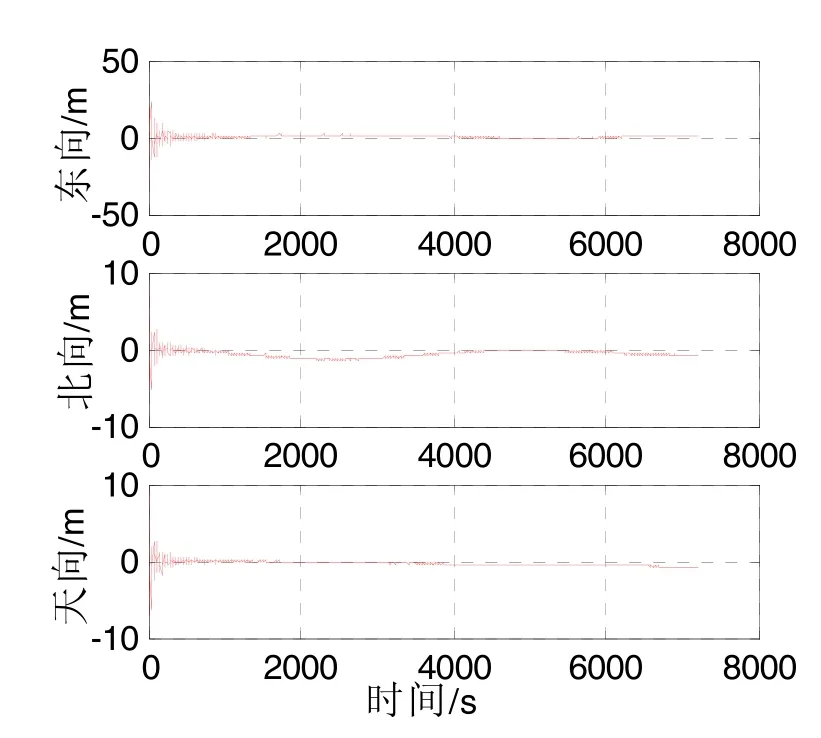
图4(a) 位置误差Fig.4(a) Position error

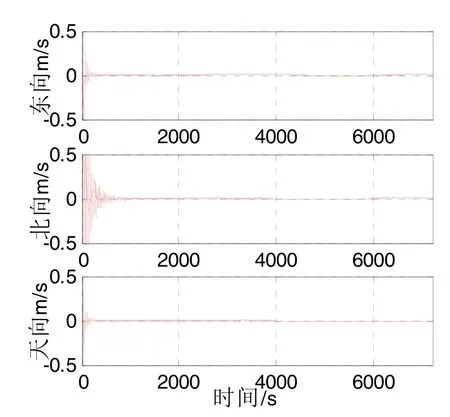
图4(b) 速度误差Fig.4(b) Velocity error

表1 组合后位置误差比较Tab.1 Comparison on position errors after combination

4 结 论

本文构造了双差分载波相位观测量，不但可以消除组合导航中若干误差源，还能避免整周模糊度的求解，但由于其本身是经过差分得到，不包含绝对位置信息，所以组合后误差不断积累发散。为提高组合导航的精度，提出了一种伪距/伪距率/双差分载波相位组合导航方法，并结合伪距/伪距率和双差分载波相位各自特点，设计了一种新的滤波器。该滤波器既发挥了载波相位高精度和伪距/伪距率包含绝对信息的优势，又有效隔离了二者的测量噪声，避免了双差分载波相位高精度被伪距高噪声“淹没”。新的组合方法能够满足无区域限制、实时导航的要求。最后利用 GPS实测数据和仿真惯性导航数据进行组合导航试验。试验中对比了伪距组合、双差分载波相位和本文组合导航方法。对比结果表明，本文方法具有最高组合导航精度。

（References）：

[1] Morgado M, Oliveira P, Silvestre C. Tightly coupled ultrashort baseline and inertial navigation system for underwater vehicles: An experimental validation[J]. Journal of Field Robotics, 2012, 30(1): 627-634.

[2] Qin Hong-lei, Cong Li, Zheng Xiao-dong, Liu Hai-bo. A JTIDS/INS/DGPS navigation system with pseudorange differential information transmitted over Link-16: design and implementation[J]. GPS Solutions, 2013, 17(3): 391-402

[3] Zhang Y, Gao Y. Integration of INS and un-differenced GPS measurement for precise position and attitude determination[J]. The Journal of Navigation, 2008, 61(1): 87-97.

[4] 李增科, 高井祥, 姚一飞, 王坚. GPS/INS紧耦合导航中多路径效应改正算法及应用[J]. 中国惯性技术学报, 2014, 22(6): 782-787. Li Zeng-ke, Gao Jing-xiang, Yao Yi-Fei, Wang Jian. GPS/ INS tightly-coupled navigation with multipath correction algorithm[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 782-787.

[5] 钟丽娜, 刘建业, 李荣冰, 王融 . 载波平滑伪距紧组合导航系统鲁棒自适应滤波算法[J]. 中国惯性技术学报, 2014, 22(2): 205-210. Zhong Li-na, Liu Jian-ye, Li Rong-bing, Wang Rong. Adaptive robust filtering algorithm for tightly-coupled integrated navigation system based on carrier phase smoothing pseudorange[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 205-210.

[6] Wendel J, Trommer G F. Tightly coupled GPS/INS integration for missile application[J]. Aerospace Science and Technology, 2004, 8: 627-634.

[7] 韩松来. GPS和捷联惯导组合导航新方法及系统误差补偿方案研究[D]. 长沙: 国防科学技术大学, 2010: 19-50. Han Song-lai. Novel GPS/SINS integration architecture and systematic error compensation[D]. Changsha: National University of Defense Technology, 2010: 19-50.

[8] 鲍其莲, 周媛媛. 基于UKF的GPS/SINS伪距(伪距率)组合导航系统设计[J]. 中国惯性技术学报, 2008, 16(1): 78-81. Bao Qi-lian, Zhou Yuan-yuan. Design of GPS/SINS pseudo-range (pseudo-range rate) integrated navigation system based on UKF[J]. Journal of Chinese Inertial Technology, 2008, 16(1): 78-81.

[9] 王秀森, 周红进, 张尚悦. 基于 GPS 伪距单差的舰船相对导航方法[J]. 中国惯性技术学报, 2012, 20(4) : 464-467. Wang Xiu-sen, Zhou Hong-jin, Zhang Shang-yue. Relative navigation between vessels based on GPS single difference[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 464-467.

[10] Schmidt G. Inertial navigation & GPS lecture[J]. Aerospace and Electronic Systems Magazine, 2011, 26(4): 41-41.

[11] Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399.

Integrated navigation method based on pseudo-range/pseudo-range rate/dual-differenced carrier phase

LI An1, FENG Ka-li2, QIN Fang-jun2
(1. Training Department, Naval University of Engineering, Wuhan 430033, China; 2. Electrical Engineering College, Naval University of Engineering, Wuhan 430033, China)

In order to improve the accuracy of the integrated navigation system, this paper proposes an integrated navigation method based on pseudo-range/pseudo-range rate/dual-differenced carrier phase. By constructing dual-differenced carrier phase observation, some errors in the integrated navigation are eliminated, and the integer ambiguity is avoided. In order to avoid the error accumulation after combination, which could introduce the pseudo-range/pseudo-range rate information, a new filter is designed. The filter takes advantages of the carrier phase’s high-precision and the superiority of pseudo-range’s containing absolute information. Finally, an integrated navigation experiment is conducted with the GPS test data and the inertial navigation data from simulation. The pseudo-range combination, dual-differenced carrier phase combination and other common integrated navigation methods are compared in the experiment. The results show that the average level positioning accuracy of the proposed method is 61.13% higher than that of the traditional pseudo-range combination method, showing that the method is feasible.

integration navigation; strap-down inertial navigation; dual-differenced carrier phase; pseudorange; pseudo-range rate

U666.1

：A

2015-06-11；

：2015-09-10

国防预研基金项目（4010103010101）；国家自然科学基金项目（61503404）

李安（1961—），男，教授，从事导航、制导与控制研究。E-mail：fengkali@126.com

1005-6734(2015)05-0602-05

10.13695/j.cnki.12-1222/o3.2015.05.009