基于地平仪两轴姿态测量的卫星自主相对导航

任家栋，曾庆双，朱 虹，丰保民

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 上海航天控制技术研究所，上海 201109；3. 上海市空间智能重点实验室，上海 201109）

基于地平仪两轴姿态测量的卫星自主相对导航

任家栋1,2,3，曾庆双1，朱 虹2,3，丰保民2,3

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 上海航天控制技术研究所，上海 201109；3. 上海市空间智能重点实验室，上海 201109）

针对近圆轨道编队卫星，提出了一种仅需要地平仪两轴姿态测量的卫星自主相对导航滤波方法，利用星间相对测量与偏航姿态运动的弱相关性，解决了欠偏航量测下的相对位置估计以及三轴姿态确定问题。可观性分析证明了该方法的可行性及对编队构型参数的适应性。大量仿真表明，对于绕飞和伴飞构型，该方法均收敛，性能特性与理论分析一致。针对当前典型的地平仪与星间测量能力，相对位置滤波精度均优于2 m（3σ），绕飞构型偏航姿态精度优于1.0°（3σ），伴飞构型偏航姿态精度优于0.5°（3σ），是对中等精度编队卫星配置简化的有益探索。

编队飞行；滤波；相对导航；自主；可观性

卫星编队飞行一直以来都是国内外的研究热点。卫星间相互合作，共同完成空间任务，具备低成本，高灵活性，高可靠性的明显优势。当前卫星编队飞行主要应用于多星立体成像、合成孔径雷达等领域[1]。

如何提高卫星的自主编队能力，以降低对地面测控资源的依赖，并获得远高于地面测控精度的编队性能，越来越得到人们的关注。作为卫星自主编队的关键技术，自主相对导航一直是编队飞行的活跃领域，圆轨道近距离下经典 CW 方程描述相对运动优势明显，基于CW方程相对导航研究的成果也最多。针对空间非合作目标，星间测量设备主要采用微波/激光雷达[2]、光学相机[3]等，得到高精度的相对测量。通常相对测量的输出形式为极坐标测量，包括星间距离+相对角度，也使得相对导航算法多采用EKF（扩展卡尔曼滤波）算法[4-5]。差分GPS[6-7]，LIDARs单元[8]等主要应用于合作目标卫星编队，依靠星间链路得到高精度的相对位姿测量。目前自主相对导航研究均基于全维的卫星本体姿态测量信息，对卫星姿态确定系统要求较高[9]。通常情况下星敏感器能够提供全维的三轴姿态测量，但地平仪、太阳敏感器等仅可提供两轴姿态测量。与姿态测量最小系统配置的研究类似[10]，在缺维姿态测量的情况下，卫星自主相对导航最小系统配置需求的研究同样意义重大。

本文针对中等精度的自主编队卫星，提出了一种基于地平仪两轴姿态测量的卫星自主相对导航方法，引入星间测量解决地平仪对偏航姿态不可观的问题，最终实现稳定的姿态确定和相对位置速度估计。文中首先进行姿态和相对运动的动力学以及星间测量和地平仪测量方程建模，然后进行系统可观性理论分析，最后通过仿真验证理论分析正确性及算法性能。

1 欧拉角描述的姿态运动方程

设ω为卫星的空间旋转角速度矢量，即为星体坐标系相对于地心惯性坐标系的角速度；ωbo表示星体坐标系相对于轨道坐标系的旋转角速度在本体系上的分量；ωoi表示轨道坐标系相对于地心惯性坐标系的旋转角速度在轨道坐标系中的分量，表示为则卫星姿态运动学方程可表示为

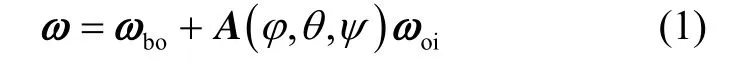
展开表示为

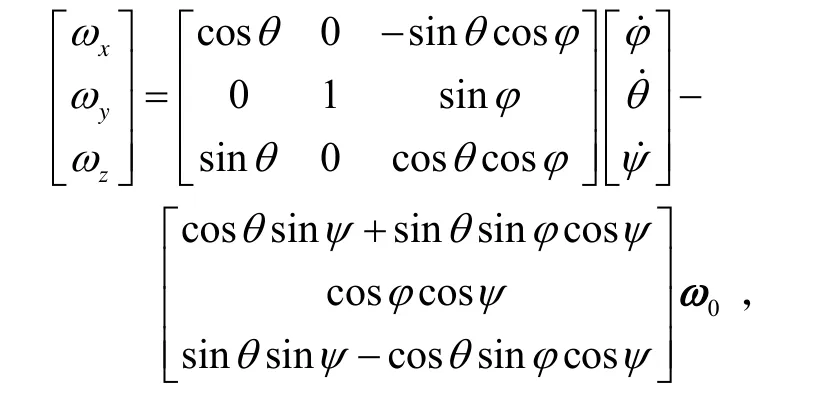
不考虑挠性，星体姿态动力学模型为

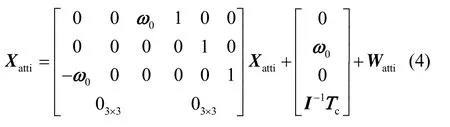
式中，Watti表示外干扰力矩等未建模误差，可用高斯白噪声近似建模。

2 相对运动方程

卫星编队中，配置雷达等星间测量设备的卫星为追踪星，另一颗卫星为目标星。相对运动坐标系定义为追踪星轨道系，O为质心，OZ指向地心，OY指向轨道面法线反方向，OX满足右手定则，如图1所示。

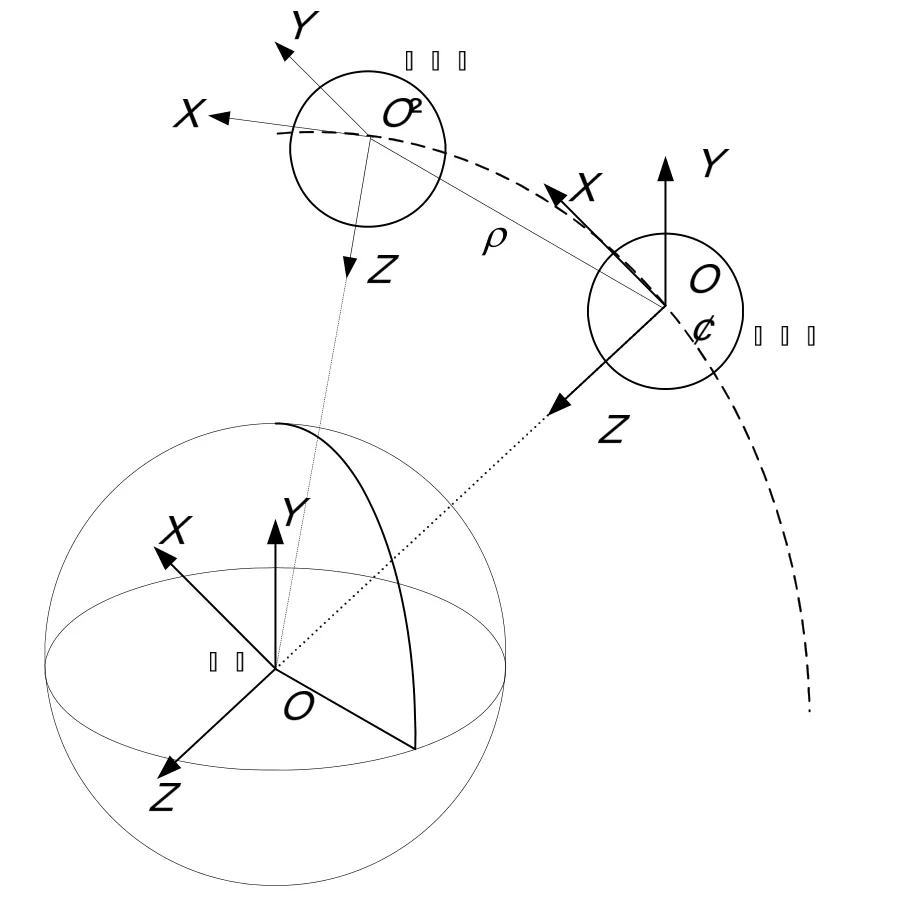
图1 相对运动坐标系Fig.1 Relative motion reference frame

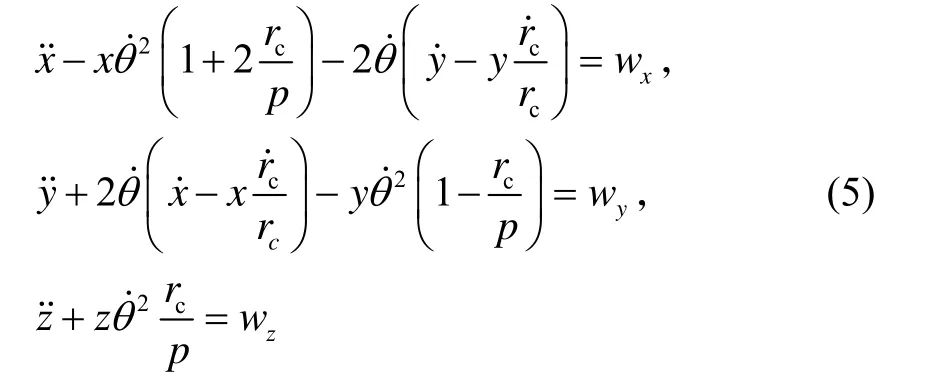
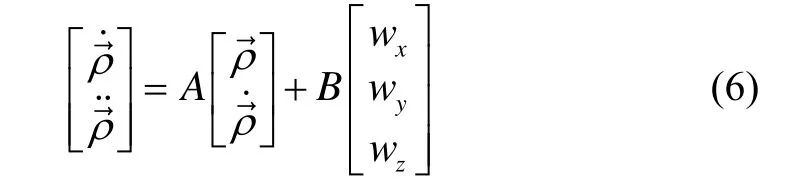
采样时间T，将上式离散化后，状态转移矩阵表示为：

通常情况下，卫星在轨轨道角速度较小，离散化后过程噪声可简化为：

3 星间测量模型

雷达是星间测量的常用单机，常用的测量输出为极坐标输出，如下式：

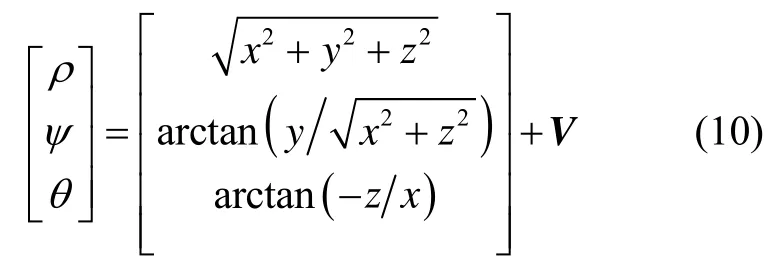
式中，ρ为两星的视线距，ψ雷达测量航向角，θ雷达测量俯仰角，V为测量噪声信号，根据某实际系统，取

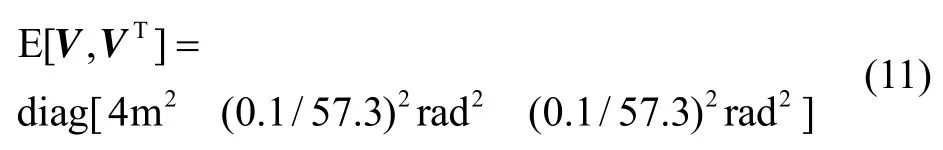
将雷达测量坐标系下的测量值转化到轨道坐标系下，形成间接测量[1]，可简化观测阵的计算过程。雷达测量值到轨道坐标系下的映射关系为非线性转换，如下：

取其一阶形式得：

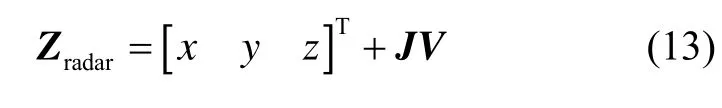
4 滤波系统设计

取状态变量，

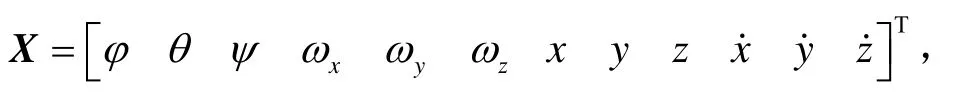
联立卫星姿态和相对运动动力学方程式(5)、(7)，为滤波系统的状态方程。

地平仪测量方程为

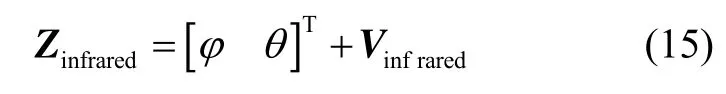
式中，Vinfrared表示地平仪测量噪声，根据某实际系统，取

得其观测阵为

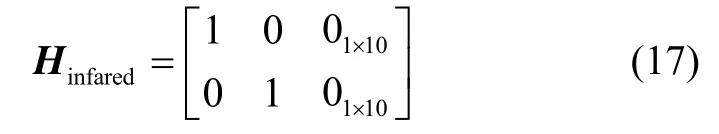
雷达观测方程可进一步改写为

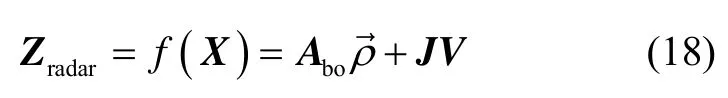
对状态变量求偏微分，可得下式：

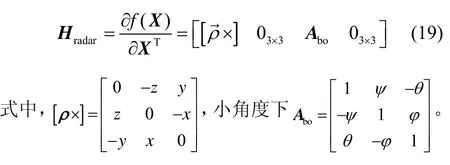
状态方程如式(5)、(7)，观测方程如式(13)、(15)，组成卡尔曼滤波系统。采用扩展卡尔曼滤波算法实现状态变量的预测与修正，系统噪声矩阵选取如式(9)、(11)、(16)。

5 系统观测性分析

滤波系统的可观性是其稳定收敛的主要判据，Gram矩阵常用来分析系统的可观性，其奇异值不仅能够反映出观测矩阵的秩，而且奇异值大小能够反映出可观测度的大小。

定义归一化的Gram矩阵：

对Gram矩阵ϑ进行奇异值分解：

式中，S为由奇异值组成的对角阵。若rank(S)=n，则系统完全可观；相反，若S秩不等于n，则系统在此点上不可观测。S的每一个奇异值与对应V中的列，且每一列的元素对应状态量。对应最大奇异值的列包含最多的观测信息，而且与此列中最大元素对应的状态观测量可观测度是最高的。简而言之，与较大的奇异值对应的状态量，其可观测性就较好；反之，对应最小奇异值的列包含最少的观测信息，与此列中最大元素对应的状态量可观测性最差[2]。

绕飞和伴飞是空间编队的两类典型构型，分析两种构型的最差可观特性，即最小奇异值特性，得到当前滤波系统的适应特性。

相对运动学分析可知，空间相对运动构型的面内（轨道坐标系XOZ面）和面外（轨道坐标系±Y向）运动解耦，且近似符合简谐振动。进一步描述为

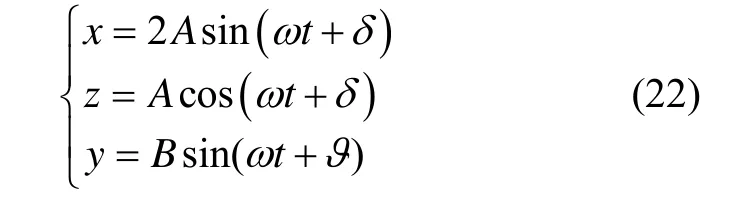
相对运动满足近似比例特性，因此两种编队构型均可采用两个参数进行统一定义：构型面外尺度比例及相角

针对两种典型组合进行分析得图2至图5。

分析可见，伴飞构型的可观性远优于绕飞构型。绕飞构型的可观性与构型的相角及比例相关性大，相角 9 0°/270°下可观性最好，面外构型比例 0 .3附近可观性最好。伴飞构型的面外尺度比例与系统可观性正相关，但随着比例增大，相关性减弱。

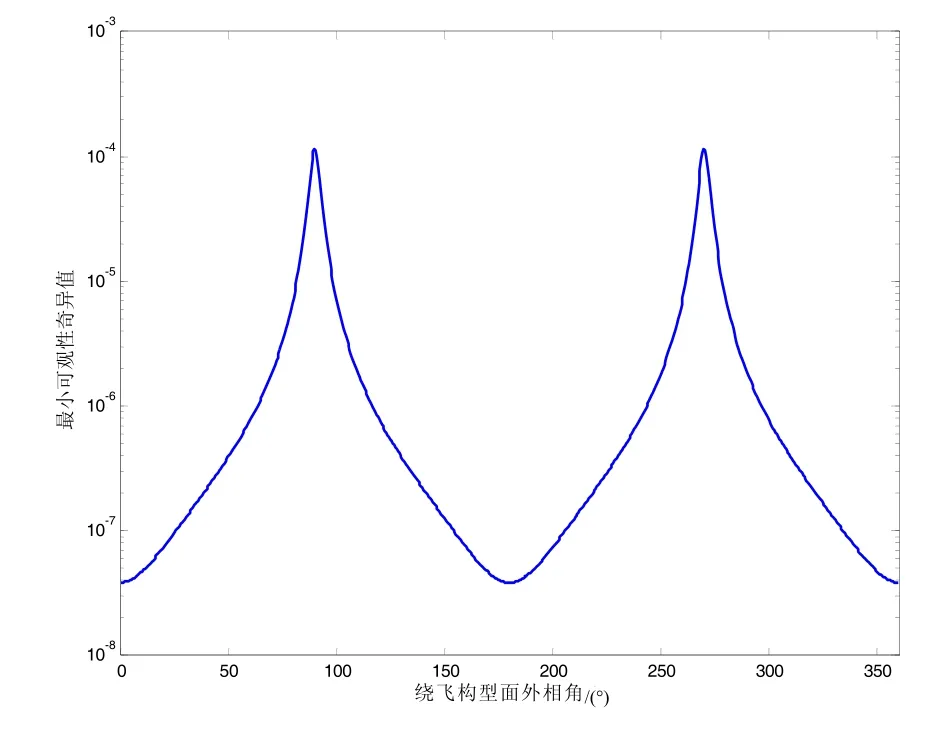
图2 绕飞构型可观性奇异值与相角关系Fig.2 Singular value of flying-around configuration with its phase angle

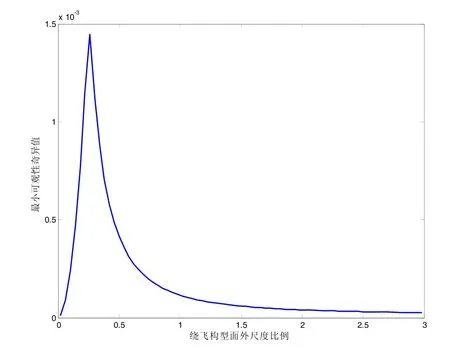
图3 绕飞构型可观性奇异值与构型尺度关系Fig.3 Singular value of flying-around configuration with its scale

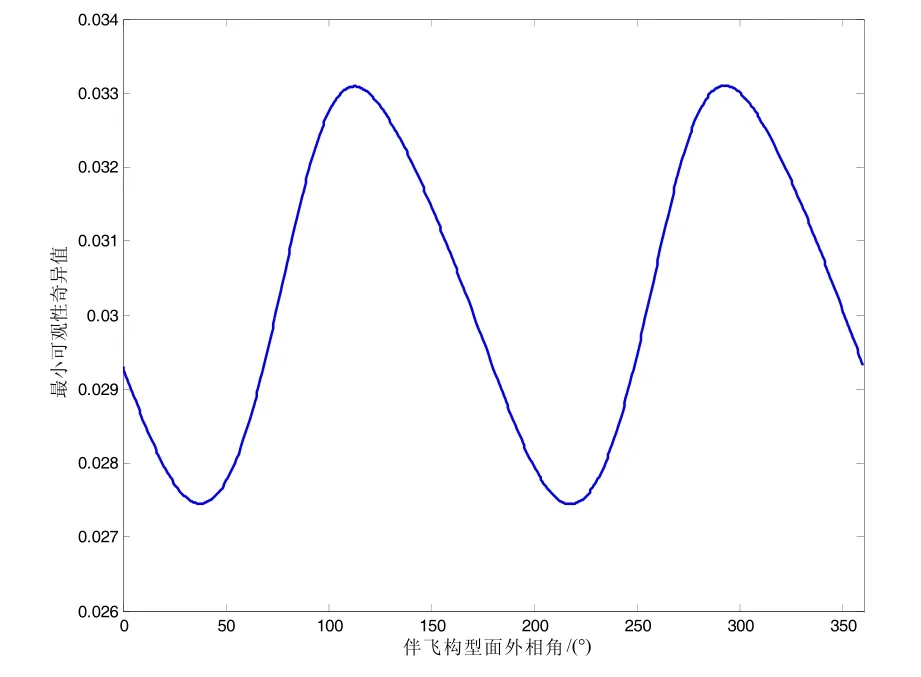
图4 伴飞构型可观性奇异值与相角关系Fig.4 Singular value of flying-companion configuration with its phase angle

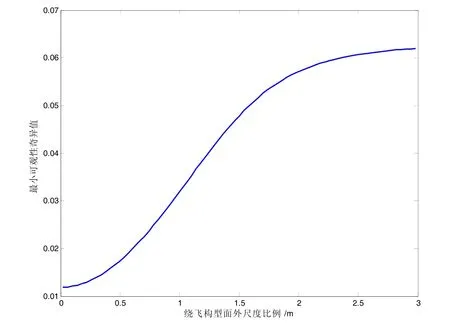
图5 伴飞构型可观性奇异值与构型尺度关系Fig.5 Singular value of flying-companion configuration with its scale

6 仿真与验证

利用数值仿真对滤波算法进行验证，针对绕飞和伴飞两种编队构型设计仿真试验。根据当前敏感器性能，配置地平仪测量误差0.2°(3σ)，星间测距误差15 m (3σ)，测角误差0.1° (3σ)，卫星运行轨道高度500 km。

针对绕飞和伴飞两种常用编队构型，设计两种仿真工况，各工况具体参数如表1所示。

表1 滤波估计精度值(3σ)Tab.1 Precision of the filter (3σ)

工况1三轴姿态及相对位置估计误差特性见图6和图7；工况2三轴姿态及相对位置估计误差特性如图8和图9。

大量仿真分析表明，对于绕飞和伴飞编队构型，滤波系统均能收敛，并得到稳定的相对位置估计和偏航姿态估计。相对于绕飞，伴飞构型能够收敛性更好，并且稳定精度较高。针对当前典型的地平仪及星间测量能力，绕飞构型偏航姿态精度优于1.0° (3σ)，伴飞构型偏航姿态精度优于0.5° (3σ)，相对位置滤波精度均优于2 m (3σ)，满足常规卫星的编队性能需求。

图6 绕飞构型姿态滤波误差Fig.6 Attitude estimation errors of flying-around configuration

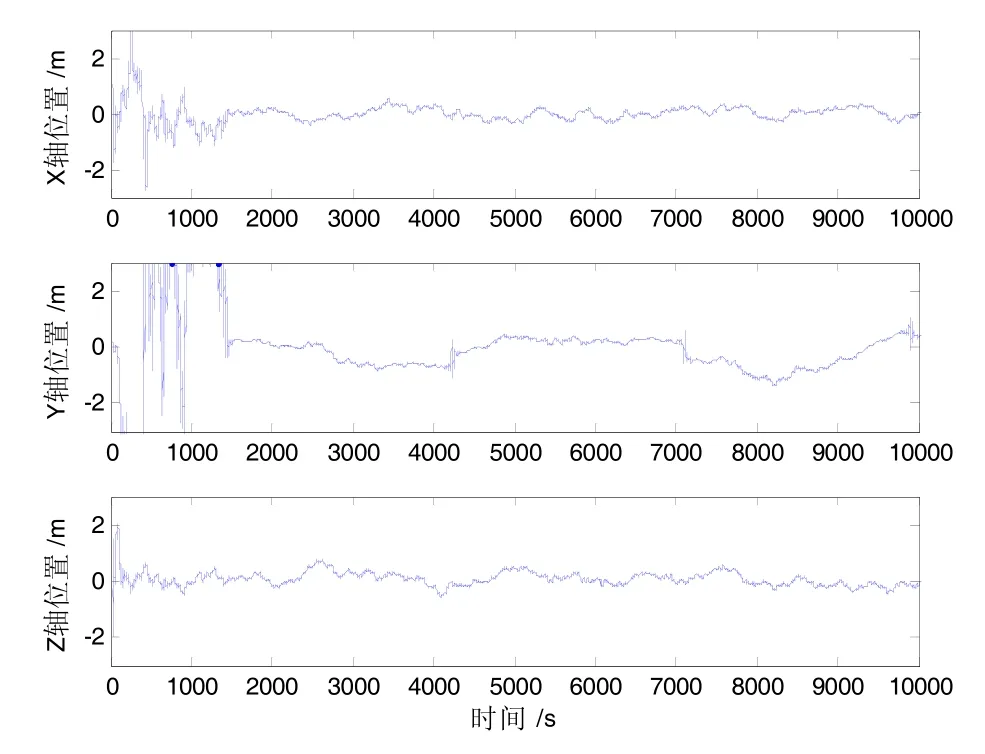
图7 绕飞构型相对位置滤波误差Fig.7 Relative position estimation errors of flying-around configuration

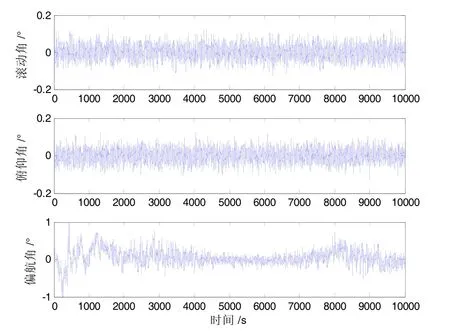
图8 伴飞构型姿态滤波误差Fig.8 Attitude estimation errors of flying-company configuration

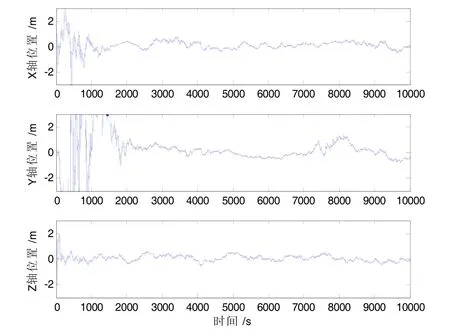
图9 伴飞构型相对位置滤波误差Fig.9 Relative position estimation errors of flying-company configuration

7 结 论

本文提出了一种仅地平仪两轴姿态测量的卫星自主相对导航滤波方法，利用星间测量与偏航姿态运动的弱相关性，联立姿态与相对运动动力学，解决了卫星偏航姿态与相对位置估计问题。对绕飞和伴飞两种典型编队构型进行了滤波系统的可观性分析，理论上证明了该方法的可行性及适应性。大量仿真表明，对于绕飞和伴飞构型，该方法均收敛，并且姿态确定和相对导航滤波性能能够满足中等精度的卫星编队需求；相对而言，伴飞构型的滤波性能远优于绕飞构型，与理论分析一致。针对当前典型的地平仪与星间测量能力，绕飞构型偏航姿态精度优于1.0° (3σ)，伴飞构型偏航姿态精度优于0.5° (3σ)，相对位置滤波精度均优于2 m (3σ)，是对中等精度姿态和编队控制需求下卫星简化星载配置的一种有益探索。

（References）：

[1] Carpenter J, Leitner J, Folta D, et al. Benchmark problems for spacecraft formation flying missions[C] //AIAA Guidance, Navigation and Control Conference and Exhibit 2003. Austin: AIAA 2003: 5364-5369.

[2] 王常虹, 曲耀斌, 任家栋, 等. 非合作编队卫星姿轨一体化滤波新方法[J]. 中国惯性技术学报, 2012, 20(6): 111-117. Wang Chang-hong, Qu Yao-bin, Ren Jia-dong, et al. New integrated attitude and orbit filter for non-cooperated satellite formation[J]. Journal of Chinese Inertial Technology, 2012, 20(6): 111-117.

[3] Lee D, Pernicka H. Vision-based relative state estimation using the unscented Kalman filter[J]. International Journal of Aeronautical and Space Sciences, 2011, 12(1): 24-36.

[4] Hablani H B, Tapper M, David D B. Guidance algorithms for autonomous rendezvous of spacecraft with a target vehicle in circular orbit[J]. Journal of Guidance Control and Dynamics, 2002, 25(3): 553-562.

[5] Kim S G, Crassidis J L, Cheng Yang , et al. Kalman filtering for relative spacecraft attitude and position estimation[J]. Journal of Guidance Control and Dynamics, 2007, 30(1): 133-143.

[6] Tancredi U, Ranga A, Grassi M. Carrier-based differential GPS for autonomous relative navigation in LEO [C]//AIAA Guidance Navigation and Control Conference, 2012-08: 4707-4717.

[7] 龚柏春, 罗建军, 马悦. 单测角相对导航的相对距离重构新算法[J]. 中国惯性技术学报, 2014, 22(3): 340-345. Gong Bai-chun, Luo Jian-jun, Ma Yue. Novel reconstructing algorithm of relative distances for angle-only relative navigation[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 340-345.

[8] Christian J A, Robinson S B, Souza C D, et al. Cooperative relative navigation of spacecraft using flash light detection and ranging sensors[J]. Journal of Guidance Control and Dynamics, 2014, 37(2): 452-465.

[9] 周朝霞, 任家栋, 曾庆双, 等. 测量最小分辨率特性下自主相对导航设计方法[J]. 哈尔滨工业大学学报, 2015, 47(3): 49-53. Zhou Chao-xia, Ren Jia-dong, Zeng Qing-shuang, et al. Autonomous relative navigation constrained by microwave radar minimum measure resolution[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 49-53.

[10] Hart C S. Satellite attitude determination using magnetometer data only[C]//47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition. 2009: 220-231.

Autonomous relative navigation with two-axis attitude measurements using only infrared earth sensor

REN Jia-dong1,2,3, ZENG Qing-shuang1, ZHU Hong2,3, FENG Bao-min2,3
(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Shanghai Aerospace Control Engineering Institute, Shanghai 200233, China; 3. Shanghai Key Laboratory of Space Intelligent Control Technology, Shanghai 200233, China)

An autonomous relative navigation method is presented for satellite formations on near circular orbit, which need only IRES (InfraRed Earth Sensor) attitude sensor and necessary inter-satellite tracking sensor. By using the existing poor relation between relative position measure and yaw attitude motion, the problem of estimating relative motion state and three-axis attitude when with loss yaw attitude information is solved. Observability analysis proves the method’s feasibility and adaptability. Simulation results indicate that the algorithm is convergent for both the fly-around and the companying formation configuration, which are consistent with the theoretical conclusion. Based on the current staple IRES and inter-satellite measure sensor, the relative position estimation error is 2 m (3σ), yaw attitude estimation error is 1.0° (3σ) for fly-around formation, and 0.5° (3σ) for accompany flight formation, which means that the method is a beneficial approach to simplify the spaceborne apparatus for medium-precision flying formation.

formation flying; filter; relative; navigation; autonomous; observability

V448.21

：A

2015-06-05；

：2015-09-21

国家高技术研究发展计划项目（2014AA8091073）

任家栋（1986—），男，博士生，从事卫星姿态确定及自主导航研究。E-mail：renjiadong@126.com

联 系 人：曾庆双（1963—），男，教授，博士生导师，主要研究飞行器控制。

1005-6734(2015)05-0597-05

10.13695/j.cnki.12-1222/o3.2015.05.008