带有初始缺陷的船体结构极限强度研究

任慧龙，郎舒妍, 任晨辉，汪 松

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150000)

带有初始缺陷的船体结构极限强度研究

任慧龙，郎舒妍, 任晨辉，汪 松

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150000)

船体结构的初始缺陷主要有初始挠度和焊接残余应力，初始缺陷对于船体的极限强度有着重要的影响。针对目前初始缺陷的模拟较为复杂的问题，寻找一种初始缺陷的简化模拟方法，采用板弯曲理论反推并模拟初始挠度，运用基于固有应变的等效载荷法模拟焊接残余应力，在此基础上应用非线性有限元法建立计及初始缺陷的船体极限强度分析方法。计算结果表明，船体结构初始缺陷对船体结构的影响不可忽略，基于固有应变的等效载荷法可较好模拟焊接缺陷。

初始缺陷；简化模拟方法；非线性有限元方法；极限强度

0 引 言

随着超大型船舶的需求增加以及新船型的深入研究，船体梁极限强度校核显得愈发重要。目前船体梁极限强度的校核方法已日趋完善，近年来应用较多的非线性有限元法，因其计算结果较为准确，能够处理复杂条件下的非线性结构力学问题，受到广泛关注。但由于有限元方法在计算分析时对焊接残余应力与初始挠度的处理大多采用简化方法，现有的计算结果并不能完全反映船体梁实际承载变形的力学特性。因此在改进计算方法时，将以上两者考虑到计算分析中以期更合理地评估船体梁极限强度。此外由于特种钢材的使用，以及焊接技术的发展，将初始缺陷考虑到船体梁极限强度计算中成为人们日益关注而有待解决的问题。船体的初始缺陷主要包括由焊接产生的残余应力以及板材的初挠度问题，早期船体结构的初始挠度模拟主要是通过特征值方法进行分析预测，预测焊接变形的方法主要有实验法、解析法、数值分析法以及等效载荷法[1]。文献[2]研究计算了具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度[2]，此方法在不同程度上对比分析了初始缺陷对船体极限强度的影响，取得了一定的成果。

本文利用板弯曲理论，推导出船体结构初始挠度的等效载荷表达式，通过基于固有应变的等效载荷法来模拟焊接残余应力，首先分析固有应变和最高温度的关系，得到相应的等效载荷，再利用MSC.Patran/Nastran有限元分析软件进行模拟计算，将焊接残余应力模拟与初始挠度模拟考虑到船体梁极限强度计算当中，最后运用非线性有限元法得到极限弯矩值并加以对比分析，结论表明，初始缺陷对船体结构影响不可忽略，本文为船体极限强度校核方法提供了一定的参考。

1 Reckling No.23模型概述

本文采用Reckling No.23模型进行计算分析，模型具体参数见表1。

表1 模型参数Tab.1 Model parameters

其中，模型的长度L=500mm。

2 初挠度模拟

2.1 概述

初始挠度模拟主要是根据板的弯曲理论，推导出船体结构初始挠度等效载荷的表达式，板的挠曲面函数在自由支持刚性周界上需满足下列条件：

(1)

(2)

通过计算得到板的挠曲线方程式为：

(3)

对于初始挠度，可以通过上述的推演方法，取m=1，n=1，得到初始挠度等效载荷的表达式：

(4)

式中：a为船体板的长边，mm；b为船体板的短边，mm，x，y为该位置的坐标。

2.2 初始挠度模拟计算分析

此例对RecklingNo.23模型进行初始挠度模拟分析。按照式(4)，模型所加载荷的公式为：

(5)

该结构的约束为模型两端加上横框架后将模型的两端延长，并将模型的两端刚固住。船体结构的初始挠度对船体结构的影响主要为垂向变形，采用MSC.Nastran软件求解结构变形量为0.911mm。

3 基于固有应变的等效载荷法的焊接残余应力模拟

3.1 概述

由焊接产生的残余塑性应变等于温度上升时产生的压缩性塑性应变与温度下降时产生的拉伸性塑性应变的和，即为焊接固有应变。固有应变等效载荷法是指求出焊接点附近的固有应变，把得到的数据在焊接断面上进行积分求出等效载荷的方法[3]。

3.2 焊接过程最高温度与固有应变间的关系

对于快速移动的大功率线热源, 在垂直于线热源方向的薄层上某确定位置的局部最高温度可以表示为：

(6)

其中：h为板厚，m；y为y方向上的坐标；q为热源的有效功率；T0为初始温度；v为焊速；c为材料的质量比热容。

在直流电压情况下, 持续作用于焊缝的热源有效热功率为：

q=ηUI。

(7)

其中：η为焊接过程中的热效率；U为电弧的电压，V；I为电弧的电流，A。

由于最高温度的不同而产生的应力大小差别，根据随温度的变化而产生变化应力的情况，固有应变值可分成以下3个方面:

当T1>Tmax时，ε*=0；

(8)

(9)

(10)

3.3 约束度概念

约束是结构对于焊接过程中输入热量后导致的热变形的抑制作用，约束度是用于表示约束强度的物理量。约束度的大小将会直接影响船体结构的焊接变形、残余应力及固有应变。基本焊接构件的约束度，一般是通过实验来求得，对于外部约束，需要通过弹性分析估算出来，约束度应为内部约束和外部约束两项结果综合计算得出。

3.4 固有应变的等效载荷

等效载荷一共包含沿焊缝垂直方向作用的横向收缩力、作用于焊缝两端的纵向收缩力、沿焊缝垂直方向作用的横向弯曲力矩和作用于焊缝两端的纵向弯曲力矩4种力组成，等效载荷可以通过对断面内分布的固有应变进行积分而求得[4]。在有限元模型中，将每一层网格简化为杆模型，则每一层的收缩力fi可以通过以下方法进行计算：

第i层的横向载荷

(11)

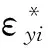
第i层的纵向载荷

(12)

以上为单层等效载荷的计算，关于横向收缩力和横向弯曲力矩，可以使用对各层的收缩力相加，使用以下方程式计算横向等效力fy和横向弯曲力矩my，其中fy和my沿焊缝施加：

(13)

(14)

对于纵向收缩力fx和纵向弯曲力矩mx，使用以下方程式进行计算，其中fx和mx作用于焊缝的两端：

(15)

(16)

具体施加载荷的方式如图1所示，实际载荷施加情况如图2所示。

图1 沿焊缝等效载荷施加的示意图Fig.1 Equivalent load along the weld

图2 载荷加载图Fig.2 Load

按照以上所叙述的方法，并结合相关约束度资料，使用C02气体保护焊进行双面连续焊接，其焊接工艺参数为：焊接电流I=300A，焊接电压U=28V，焊接速度v=40cm/min，焊角长度k=6mm。计算结构的等效载荷，计算结果如表2所示。

表2 等效载荷值Tab.2 Equivalent Load

3.5 计算分析

将上述等效载荷以及约束情况在MSC.Patran软件里施加完成，通过MSC.Nastran求解出结构的变形情况如表3所示。

表3 结构变形情况Tab.3 Structural deformation

由于横向收缩是一个平板的整体收缩，纵向变形只是在焊缝区域产生，所以实际工程中，主要注意的是焊缝的横向变形。参考其他模型的焊接变形，所得结果与本文方法数据在同一个数量级，该结果可靠性较强。

4 基于非线性有限元法的船体梁极限弯矩计算

4.1 显式动态分析的非线性有限元法

非线性有限元分析方法很好地考虑了影响船体结构极限承载能力、破坏形式的一些敏感因素，例如材料的弹塑性属性、结构的几何非线性行为以及结构的屈曲强度和后屈曲强度等[5-6]。

Abaqus/Explicit动态显式算法[7-8]是采用动力学方程的一些差分格式(如中心差分法、线性加速度方法、Newmark法和wilson法等)，不必同时求解联立方程组，每一个增量步的计算成本很低，其显式动力学求解过程如下：

1)结点计算

动力学平衡方程:

(17)

(18)

(19)

2) 单元计算

步骤3：集成单元结点内力I(t+Δt)。

步骤4：设置时间为t为t+Δt，返回步骤1。

4.2 考虑初始缺陷的Reckling No.23模型极限弯矩对比分析

基于极限强度的分析思想，图3为没有施加等效载荷的模型变形情况，图4为施加等效载荷后模型的变形情况，图5可以看出计及初始缺陷的极限弯矩要小于不计及初始缺陷的情况，表4表示二者相差的数值为0.2×109N.mm。

图3 不计初始缺陷下的极限弯矩Fig.3 Excluding the initial defect under the limit moment

图4 计及初始缺陷下的极限弯矩Fig.4 Ultimate moment count under initial defect

图5 模型转角和弯矩的关系图Fig.5 The relational model and moments corner

表4 计算结果对比分析Tab.4 Comparative analysis results

5 结 语

本文基于等效载荷法的思想，提出了一套关于计算模拟船体结构初始缺陷的分析方法，并结合RecklingNo.23模型进行考虑初始缺陷的极限强度计算结果对比分析，得到如下结论：

1)基于板弯曲理论的初挠度模拟为船体板初始挠度计算提供了有效的思路和途径。

2)模型计算结果表明基于固有应变的等效载荷法具有一定的实用性，为模拟复杂的船舶分段焊接提供了一定的参考。

3)通过Abaqus/Explicit非线性有限元分析计算得到模型的极限弯矩，对比分析2种情况下的转角弯矩图可看出，船体结构的初始缺陷对结构强度校核的影响不可忽略。

[1] 李鸿.基于固有应变的船体分段焊接变形预测[D].哈尔滨:哈尔滨工程大学,2006.

[2] 张婧，施兴华，顾学康.具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J].中国造船,54(1):60-69.

ZHANGJing，SHIXing-hua，GUXue-kang.Ultimatestrengthstudyofstiffenedplateundercomplexloadingwithinitialimperfections[J].ShipbuildingofCHINA,54(1):60-69.

[3] 李鸿，任慧龙，曾骥.预测船体分段焊接变形方法概述[J].船舶工程,2005,27(5):55-58.

LIHong，RENHui-long，ZENGJi.Generalreviewofpredictionmethodsofshipstructures′weldingdeformation[J].ShipEngineering,2005,27(5):55-58.

[4] 汪建华.固有应变有限元法预测焊接变形理论及其应用[J].焊接学报，2002,23(6):36-40.

WANGJian-hua.PredictionofweldingdistortionsbasedontheoryofinherentstrainbyFEManditsapplication[J].TransactionsoftheChinaWeldingInstitution，2002，23(6):36-40.

[5] 刘相春，李陈锋，任慧龙，等.大跨度板架屈曲分析的非线性有限元法[J].舰船科学技术，2013，35(1)：46-40.

LIUXiang-chun，LIChen-feng，RENHui-long，etal.TheNFEMforbucklinganalysisoflarge-spangrillage[J].ShipScienceandTechnology，2013,35(1)：46-40.

[6] 隋智享.船舶与海洋工程结构极限强度分析[D].大连:大连理工大学,2004.

[7] 马晓峰，ABAQUS6.11有限元分析从入门到精通[M].北京：清华大学出版社,2013.

[8] 杨平.船体结构极限强度及破损剩余强度的研究[D].武汉：武汉理工大学,2005.

Ultimate strength of hull structure with initial defect

REN Hui-long，LANG Shu-yan，REN Chen-hui, WANG Song

(Harbin Engineering University，Ship Engineering College,Harbin 150001,China)

The initial deflection and welding residual stress are the two mainly initial defects of the hull structure.Initial defect has an important implication for the ultimate strength of the hull.For the current issues of the simulation of the Initial defect.In this paper, a simplified simulation of an initial defect is proposed; the plate bending theory is used to thrust on the opposite side to simulate the initial defects.The equivalent load method based on inherent strain is used to simulate welding residual stress.On the foundation, the nonlinear finite element method is used to analysis the ultimate strength of the hull with considering the initial defects.The results show that based on the equivalent load inherent strain method can simulate weld defects and the initial defects impacts on the structure of the hull cannot be ignored.

initial defect; simplified simulation; finite element method; ultimate strength

2015-05-07；

2015-06-05

任慧龙(1965-)，男，教授，从事船舶与海洋工程结构强度和环境载荷研究。

U663.2

A

1672-7649(2015)12-0038-04

10.3404/j.issn.1672-7649.2015.12.008