高职校数学教师认识信念的维度分析与倾向性研究

程德胜，喻 平

（1．江苏联合职业技术学院 南京分院 基础部，江苏 南京 210019；2．南京师范大学 数学科学学院 课程与教学研究所，江苏 南京 210097）

高职校数学教师认识信念的维度分析与倾向性研究

程德胜1，喻 平2

（1．江苏联合职业技术学院 南京分院 基础部，江苏 南京 210019；2．南京师范大学 数学科学学院 课程与教学研究所，江苏 南京 210097）

利用数学教学认识信念二维结构量表，研究职业院校不同教龄段数学教师数学教学认识信念各个维度的情态及认识信念之间的差异性，并分析认识信念的倾向性．不同教龄段教师对13个维度的认识有共性，但差异性明显，且同一教龄段教师对同一维度的认识也呈发散情形．职业院校数学教师的数学认识信念偏向于传统客观主义数学观，教学认识信念偏向于现代相对主义教学观．数学教学认识信念和教龄存在一定程度的相关性．

职业院校；数学教师；数学教学认识信念

1 问题提出及研究意义

“‘认识信念’是个人对知识和知识认识过程的见解和信念．”数学教师的认识信念（epistemic beliefs）是教师关于数学教学的信念，主要由两种信念组成：数学认识信念和教学认识信念、数学认识信念指教学中教师对数学本体的认识，教学认识信念指教师对教学本质的认识，两者相互交织形成数学教师的认识信念倾向系统．国外，关于认识信念的研究集中在3个方面：个体认识论的发展；个体的信念系统；个体的元认知过程．关于教师认识信念研究，主要集中在：“（1）教师认识信念的概念模型；（2）教师认识信念的领域的特殊性和一般性；（3）教师认识信念与教学的联系；（4）教师认识的发展．”[1]

学者Koehler、Grouws、Fennema、Franke与Surize等的模型揭示了数学教师的教学认识信念是构成教师教学行为的因素之一（教学行为包括教师知识、教师信念、教师态度3个因素），数学教师的数学教学认识信念对教学与教学行为产生影响．该模型也揭示了关于数学学习和学生作为学习者的信念共同构成有关数学和数学教学的教师信念系统[2]．这些研究表明：数学教师认识信念反应了数学教师对数学观、数学教学、数学学习、数学本质、学生作为学习者、数学课程目标等的见解[3]．这种见解带有一点的倾向性，会在数学教学中表现出来．

国内研究关于教师认识信念与数学教师认识信念的学者主要为喻平，集中在两个方面：认识信念的形成因素[4]与数学教师认识信念的二维结构[1]．张侨平、黄毅英、林智中等学者主要关注数学教师的数学信念的研究[5]．其它方面的一些研究表明[6～9]：数学教师认识信念对其教学产生影响．

对教师认识信念的测量模型．国外学者Lisa与Deanna提出“综合个人认识论模型”[10]，国内学者喻平提出了数学教师数学认识信念测量的二维结构模型．对数学认识信念测量的对象为学生[11～12]，关于对数学教师认识信念的测量目前还没有．有关问题逐步受到越来越多的研究者的重视．

职业院校数学教师的认识信念及数学教学认识信念的研究及测量还是空白．对职业院校数学教师认识信念的真实情态及对数学教学认识信念的倾向性进行测量研究，有现实的必要性．原因在于：一是促进数学课程的有效教学，教师认识信念是有效教学的基础；二是针对性改进数学教师的认识信念；三是能为教师的职后再培训教育提供参考数据．

这里是对文[1]理论框架与量表设计创新的一种实践．

2 研究方法

2.1 认识信念的二维结构

采用文[1]的理论框架，将数学教学认识信念分为数学认识信念和教学认识信念两个维度，从而构成了一个二维结构，模型如图1[1]：横轴代表教学认识信念（X轴），纵轴代表数学认识信念（Y轴）．

4个象限分别代表4种不同的数学教学认识信念（图1的4个象限标示），根据二维结构模型可以检测数学教师对数学教学认识信念的倾向性．

2.2量表编制

量表编制（问卷）的理论与实践依据为：数学认识信念依据Ernest的数学教师的数学观念分类原则；教学认识信念依据“学习要义”[1]的实质性解释（对此解释，详见文[1]）．具体地，数学认识信念由数学的真理性、价值性、客观性、结构性4个维度组成，教学认识信念由教学目的、教学本质、教学方法、教学操作、教学评价、学习本质、学生角色、学习能力、影响学生学习因素9个维度组成．每个维度编制一个问题，共计13个问题，每个问题的答案是唯一的，每个问题包含5个陈述句，每个陈述句分别对应维度中的一种倾向（观念）．量表的13个问题，有的问题用正向提问方式，有的问题则为反向提问方式．

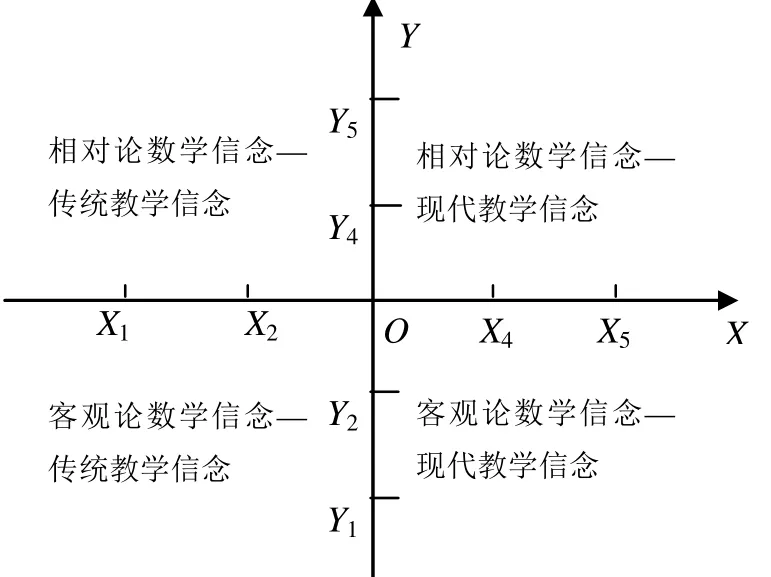
图1 教师信念倾向性二维结构

2.3量表编码

为便于统计与说明，问卷进行如下编码．M1、M2、M3、M4分别对应“对数学真理性认识、对数学价值性认识、对数学客观性的认识、对数学结构性的认识”，相应地M1i、M2i、M3i、M4i（i=1, 2, 3, 4, 5）分别对应数学认识信念中每个维度的5种倾向．T1、T2、T3、T4、T5、T6、T7、T8、T9分别对应“数学课程三维目标、对教学本质的认识、对教学方法的认识、对教学操作的认识、对学习评价的认识、对学习本质的认识、对学生角色的认识、对学生学习能力的认识、对影响学生学习因素的认识”，相应地，T1j、T2j、T3j、T4j、T5j、T6j、T7j、T8j、T9j（j=1, 2, 3, 4, 5）分别对应教学认识信念每个维度的5种倾向．M表示数学认识信念，T表示教学认识信念，MT表示数学教学认识信念．

2.4量表数据处理

利用SPSS19.0对问卷进行数据处理分析．第一，利用已编码的问卷，建立数学教学认识信念的子量表（13个维度）和两个分量表M、T以及总量表MT，每个维度按照认识信念从传统到现代的5种倾向，分别用1、2、3、4、5定序，利用描述统计直方图、t检验，分析认识信念的维度状态以及不同教龄的数学认识信念、教学认识信念、数学教学认识信念的差异．第二，建立数学教学认识信念倾向性数据，分析教师的数学教学认识信念的倾向性，采用文[1]的第二种计分方法：

2.5 测试过程

以南京市几所高职校106名相关数学教师为测试对象，测试分三步进行．第一步，预测，对20名对象进行预测，分析子量表之间是否存在相关性，找出存在相关性的问题（T3与T5、T4与T5、T2与T8），然后进行修正．第二步，验证测试卷的信度与效度，选取20名被试对象，进行了两次测量，间隔时间为10天．第三步，对其余的86名教师进行测试，发放问卷86份，收回66份，加上第一步20名被试的第二次测量卷，共计收回有效问卷86份（1—5年、6—10年、11—21年、21年以上4个教龄段测试卷分别为22、29、20、15份）．

2.6 信度和效度检测

2.6.1 信度检测

“二维结构的数学教学认识信念量表，适合用重测信度考量”[1]．对被试对象进行两次测量，然后分别计算在4个象限的得分，第一次测试，每名对象4个象限的得分记为S11、S21、S31、S41，第二次测试，每名对象4个象限的得分记为S12、S22、S32、S42，然后计算两次结果的相关系数．经计算，重测信度为0.812，S11与S12、S21与S22、S31与S32、S41与S42之间的相关系数分别为0.997**、0.953**、0.983**、0.954**（**表示在0.01水平（双侧）上显著相关，下同）．因此，量表具有很好的信度．

2.6.2 效度检测

从表1和表2可以看出子量表M1、M2、M3、M4之间；子量表T1、T2、T3、T4、T5、T6、T7、T8、T9之间；M、T、MT之间在0.05水平上存在弱相关．可以利用结构效度进行检测．

效度检测的依据是根据文[1]的效度检测标准，即计算总量表、分量表、子量表两两之间的相关系数．

首先，检验两个分量表之间，以及分量表与总量表之间的相关．经检验，M与T、M与MT、T与MT的相关系数分别为0.444**、0.808**、0.887**．分量表M与T之间的相关分别小于分量表M、T与总量表MT之间的相关．

其次，检验分量表与所属子量表之间以及总量表与子量表之间的相关（表1、表2）．可以看出分量表与所属子量表的相关大于子量表与总量表之间的相关．

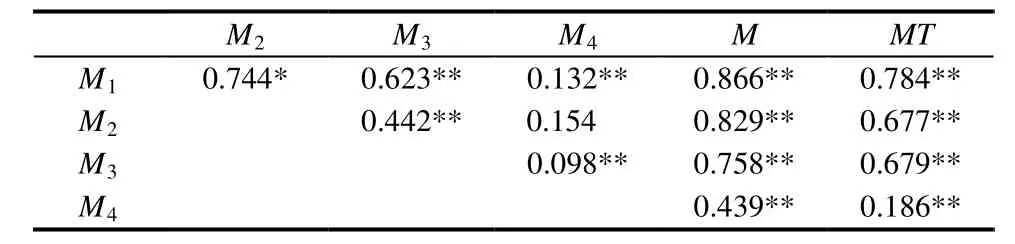
表1 分量表M的结构效度分析

最后，检测子量表之间的相关，由表1可知子量表M1、M2、M3、M4之间的相关小于分量表M与总量表MT之间的相关0.808．由表2可知子量表T1、T2、T3、T4、T5、T6、T7、T8、T9）之间的相关也小于分量表T与总量表MT之间的相关0.887．

综合以上相关系数可以得出量表具有较好的结构效度．

2.7 研究假设

高等职业院校教师的数学认识信念更多表现为客观主义认识信念，教学认识信念上更多表现为现代相对的教学认识信念；教师的认识信念有一个发展过程，不同教龄的教师其认识信念有差异．

表2 分量表T的结构效度分析

3 调查结果分析

3.1群体认识信念13个维度的情态分析

对数学真理性的认识（M1）．（见图2）

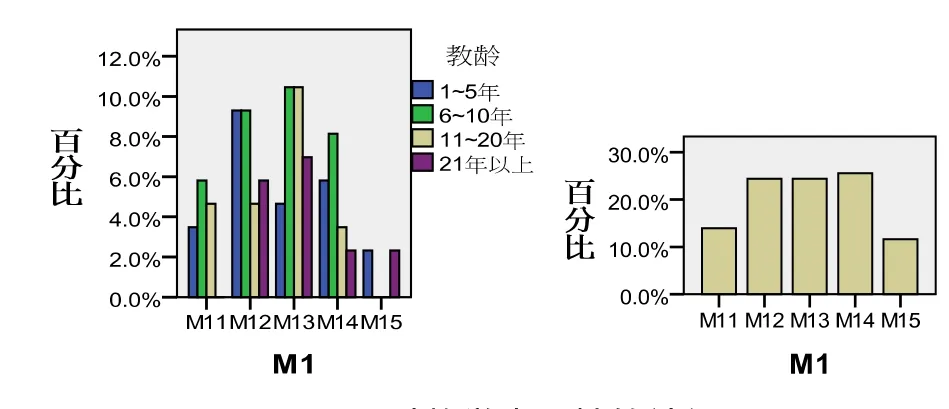
图2 对数学真理性的认识

教龄1—5年的教师持多元绝对论、相对性绝对论、分离的相对性绝对论（人数依次降低，下同）；教龄6—10年教师主要观点为：分离的相对性绝对论、多元绝对论、联系的相对性绝对论；教龄10—21年教师观点主要为：分离的相对性绝对论、多元绝对论、二元绝对论；教龄21年以上教师的观点主要为：分离的相对性绝对论、多元绝对论．群体对数学真理性认识的观点主要为多元绝对论、分离的相对性绝对论、联系的相对性绝对论．

对数学价值性的认识（M2）．（见图3）

图3 对数学价值性的认识

所有教师的主要观点为分离的相对性绝对论，其次为相对性绝对论．

对数学客观性的认识（M3）．（见图4）

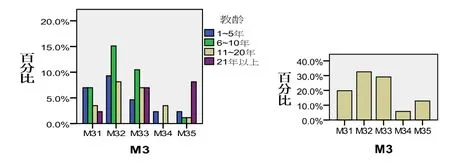
图4 对数学客观性的认识

教龄1—5、6—10年教师的观点依次为：多元绝对论、二元绝对论、分离的相对性绝对论；10—21年教师的观点依次为：多元绝对论、分离的相对性绝对论、联系的相对性绝对论；21年以上教师观点依次为：相对可误论、分离的相对性绝对论．群体的观点依次为：多元绝对论、分离的相对性绝对论、二元绝对论、相对可误论，认识比较分散．

对数学结构性的认识（M4）．（见图5）

图5 对数学结构性的认识

教龄1—5的教师主要持分离的相对性绝对论；6—10年教师的认识相对分散，主要认为持联系的相对性绝对论；11—21年教师的观点依次为联系的相对性绝对论、分离的相对性绝对论；21年以上教师观点主要持分离的相对性绝对论．群体的认识呈现出分散状态，主要观点为分离的相对性绝对论或联系的相对性绝对论，其次为多元绝对论和二元绝对论．

对教学目的的认识（T1）．（见图6）

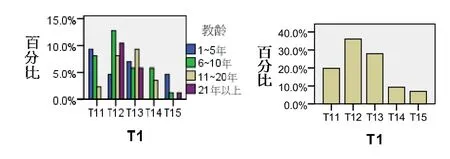
图6 对教学目的的认识

1—5年教师的观点依次为：行为主义、信息加工建构主义；6—10教师的观点依次为：认知主义、行为主义；11—21年教师的观点依次为：信息加工建构主义、认知主义．群体的观点依次为：认知主义、信息加工建构主义、行为主义．

对教学本质的认识（T2）．（见图7）

1—5年与6—10年教师的观念主要持认知主义；11—21年教师的观点依次是：信息加工建构主义、个人建构主义教学观、认知主义；21年以上教师主要持行为主义教学观．群体主要是认知主义教学观．

对教学方法的认识（T3）．（见图8）

图7 对教学本质的认识

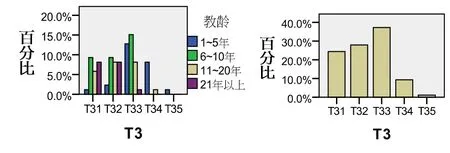
图8 对教学方法的认识

1—5年教师的观点依次为：信息加工建构主义、个人建构主义；6—11年教师的观点依次为：信息加工建构主义、认知主义、行为主义；11—21年教师的观点依次为：信息加工建构主义、认知主义；21年以上教师观点依次为：认知主义、行为主义．群体的认识依次为：个人建构主义、认知主义、行为主义教学法．

对教学操作的认识（T4）．（见图9）

图9 对教学操作的认识

1—5年教师的观点依次为：个人建构主义、社会建构主义；6—10年教师的观点依次为：认知主义、信息加工建构主义；11—21年教师的观点依次为：行为主义、个人建构主义、认知主义．群体教师的观点依次为：个人建构主义、认知主义、信息加工建构主义、行为主义．

对教学评价的认识（T5）．（见图10）

图10 对教学评价的认识

1—5年教师的观点主要信息加工建构主义；6—10年教师的观点依次为：认知主义、信息加工建构主义、行为主义；11—21年教师的观点依次为：信息加工建构主义、认知主义；21年以上教师的观点依次为：信息加工建构主义、认知主义．群体的观点依次为：信息加工建构主义教学评价、认知主义教学评价．

对学习本质的认识（T6）．（见图11）

图11 对学习本质的认识

1—5年和6—10年教师认识相对分散，1—5年教师主要持社会建构主义观；6—10年教师主要持个人建构主义观；11—21年教师主要持认知主义观；21年以上教师观点主要持个人建构主义观．群体的认识依次为个人建构主义、认知主义、信息加工主义．

对学生角色的认识（T7）．（见图12）

图12 对学生角色的认识

1—5年教师主要持双主体观（信息加工建构主义）；6—10年教师主要认为“教师是知识的传播者，学生是知识的接受者”（行为主义）与“教师是引导者，学生是参与者”（认知主义）；11—21年教师的观点分布均匀，表现为“个人建构主义”（“教师是评价者，学生是探究者”）、“信息加工建构主义”、“认知主义”与“行为主义”；21年以上教师观点为“信息加工建构主义”．群体的认识相对集中，表现为“双主体观”．

对学习能力的认识（T8）．（见图13）

图13 对学习能力的认识

教师的主要观念：1—5年教师：认知主义；6—10年教师：信息加工建构主义；11—21年教师：个人建构主义和社会建构主义；21年以上教师：认知主义．群体的主要认识依次为认知主义、信息加工建构主义、个人建构主义．

对影响学生学习因素的认识（T9）．（见图14）

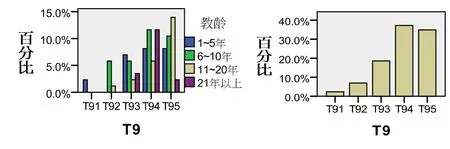
图14 对影响学生学习因素的认识

1—5年教师认识分散，主要观点为个人建构主义、社会建构主义、信息加工建构主义；6—10年教师的观点为个人建构主义、社会建构主义；11—21年教师的观点为社会建构主义；21年以上教师观点为个人建构主义．群体的认识为社会建构主义．

综合结果见图15．

图15 综合结果

1—5年教师整体的数学认识信念相对分散，主要偏向于联系的相对性绝对论，其次为分离的相对性绝对论和多元绝对论；6—10年与11—21年教师整体的数学认识信念偏向于联系的相对性绝对论和分离的相对性绝对论；21年以上教师整体的数学认识信念主要为分离的相对性绝对论，其次为多元绝对论．对于教学认识信念，1—5年教师整体的教学认识信念也很分散，且差距不大，依次为信息加工建构主义、个人建构主义、认知主义、社会建构主义、行为主义；6—10年与11—21年教师整体的教学认识信念较为一致，主要为认知主义、个人建构主义以及信息加工建构主义；21年以上教师整体的教学认识信念主要为个人建构主义、信息加工建构主义、认知主义．

3.2 群体间认识信念状态差异

以M、T、MT作为因变量，教龄作为固定因子，利用多因变量分析4个教龄段教师在数学认识信念（M）、教学认识信念（T）、数学教师认识信念（MT）之间的差异性（见表3）．

表3 差异性结果统计

6～10年 11～20年-0.517 6* 1.265 63 0.710 21年以上-2.483 3* 1.432 15 0.000 11～20年21年以上-1.965 7* 1.614 17 0.027

3.3 群体数学教学认识信念倾向性分析

3.3.1 群体间数学教学认识信念倾向性的差异性

对不同教龄段教师的得分进行多因变量方差分析（见表4）．在表3中，由显著性可知，在“相对论数学信念—现代教学信念”倾向性上，1—5年与11—21年、6—10年与11—21年两对组别之间存在显著性差异．在“相对论数学信念—传统教学信念”倾向性上，1—5年与6—10年、1—5年与11—21年、6—10年与21年以上、11—21年与21年以上4对组别之间存在显著性差异．在“客观论数学信念—传统教学信念”倾向性上，4个教龄段之间无显著差异．在“客观论数学信念—现代教学信念”倾向性上，1—5年与6—10年、1—5年与11—21年、11—21年与21年以上4对组别之间存在显著性差异．

表4 多因变量方差分析统计

3.3.2 教师整体数学教学认识信念倾向性各象限得分均值如表5所示．

教龄第一象限第二象限第三象限第四象限1—5年6.375 06.437 56.781 36.343 86—10年7.636 49.272 75.666 74.606 111—20年10.705910.588 24.764 73.117 6

21年以上5.500 03.500 05.250 07.250 0总计7.674 48.209 35.883 75.081 4

1—5年教师，第三象限均值6.781 3为最高，该教龄段教师的数学教学认识信念倾向为“客观论数学信念—传统教学信念”，即在数学信念的认识上倾向于多元绝对论、分离的相对性与二元绝对论，而在教学信念上倾向于认知主义、信息加工主义或行为主义．但又看到其它3个象限均值与第三象限的均值相差不大，说明该教龄段教师的数学教学认识信念倾向性分散．

6—10年教师，第二象限的均值9.272 7为最高，大于其它3个象限的均值，说明该教龄段的教师其数学教学认识信念更倾向于“相对论数学信念—传统教学信念”，即数学认识信念上倾向于多元绝对论或分离的相对性绝对论，而教学认识信念上倾向于信息加工建构主义、个人建构主义或社会建构主义．第一象限的均值为7.6364，说明该教龄段有相当部分教师的数学教学认识信念已逐渐演变为“相对论数学信念—现代教学信念”．

11—21年教师，第一象限的均值10.705 9为最高，第二象限的均值为10.588 2，大于其它两个象限的均值，说明该教龄段教师的数学教学认识信念主要为“相对论数学信念—现代教学信念”或“相对论数学信念—传统教学信念”，即相当一部分教师的数学认识信念都倾向于分离的相对性绝对论、联系的相对性绝对论或相对可误论，但在教学认识信念上呈现出两极分化的情态，一部分教师持行为主义、认知主义，而另一部分的教师则持个人建构主义、社会建构主义．

21年以上教师，第四象限的均值为7.250 0，大于其它3个象限，群体的数学教学认识信念表现为“客观论数学信念—现代教学信念”，即数学认识信念倾向于多元绝对论或分离的相对性绝对论，甚至二元绝对论，教学认识信念倾向于信息加工建构主义、个人建构主义或社会建构主义．其次第一象限均值为5.500，大于第二或第三象限均值，说明有相当部分教师的数学教学认识信念为“现代教学信念—相对论数学信念”．比较而言，教龄21年以上教师的数学认识信念呈两种极端状态．

总体上，第二象限均值为8.209 3，说明总体上所有教师的数学教学认识信念倾向于“相对论数学信念—传统教学信念”，数学认识信念倾向性上依次是联系的相对性绝对论、分离的相对性绝对论或相对可误论，而教学认识信念倾向性上依次是行为主义、认知主义、信息加工建构主义．但同时也看到，第一象限的均值7.674 4，大于第三象限和第四象限的均值，总体上显示有相当数量教师的数学教学认识信念表现为“相对论数学信念—现代教学信念”．

4 讨论与结论

4.1 讨 论

从二维结构角度研究职业院校教师的数学教学认识信念的倾向和情态是一种创新．研究教师的数学教学认识信念在以下两方面有积极意义：一是有效教学，教师的数学教学认识信念是有效教学的前提；二是教师专业发展与职后培训的针对性，从教师的数学教学认识信念方面入手，可以提升专业发展与培训的针对性．在职业院校，到目前为止，从教师的认识信念方面讨论上述两个问题，目前的研究仍是空白．

对于改变或促进职后教师的认识信念，综合近年来的研究，主要有4种观点：（1）通过增加教师对学生认知方式的了解，来促进改变教师信念．创设合作学习环境，促进教师信念改变[13]．（2）设置丰富多维的课程，依托能激发教师质疑和批判精神的问题，展开讨论，以期改变教师的信念[14]．（3）促进、完善教师的MPCK[15～16]．（4）加强对数学经验性与演绎性的认知研究[17]．

在职业院校，要完善教师的数学教学认识信念，除要很好地吸收上述学者提出的观点外，以下几点也是要考虑的．一是职业院校中影响教师数学教学认识信念的“职业的因素”，例如，数学课程的定位、数学课程目标的追求等．二是研究改进教研培训模式，从以往注重教材内容与教法转向更多关注教师的教学行为及反思后的行为跟进．三是数学教学认识信念的转变，教师个人的反省应当成为常态，不能局限于教学经验的积累，要时刻反省自己的数学教学理念，实现数学教学文化更新与再造．四是很有必要加强数学教师在数学（教育）哲学、数学方法论、数学教育心理学、数学文化等方面的系统学习和实践．

4.2 结 论

（1）所有教师的数学教学认识信念倾向于“相对论数学信念—传统教学信念”，同时有相当数量教师的数学教学认识信念表现为“相对论数学信念—现代教学信念”．

（2）在1—5年、6—10年、11—21年3个教龄段，教师的数学教学认识信念倾向性呈现出数学教学认识信念演变的历史：传统教学信念—客观论数学信念→传统教学信念—相对论数学信念→现代教学信念—相对论数学信念．

（3）数学认识信念更多表现为客观主义认识信念（二元绝对论或多元绝对论），教学认识信念上更多表现为现代相对的教学认识信念（信息加工建构主义、个人建构主义或社会建构主义）．

（4）总体上，所有教龄段教师数学教学认识信念的倾向性呈现出与教龄相关联的特点．1—5年的教师虽然整体的认识倾向为传统教学信念—客观论数学信念，但其在4个象限的均值相差无几，说明该教龄段教师的数学教学认识信念与其群体处于专业发展的初期存在相关性．6—10年与11—21年教师的认识信念倾向性与该群体教师处于专业发展的成熟期、高峰期有相关性．教龄21年以上教师，数学认识信念与教龄有一定关系．

[1]喻平．数学教师认识信念的一个理论框架与量表设计[J]．数学教育学报，2013，22（4）：34-37．

[2] Suriza van der Sandt. Research Framework on Mathematics Teacher Behaviour [J]. Eurasia Journal of Mathematics, Science&Technology Education, 2007, 3(4): 343-350.

[3] Valanides N, Angeli C. Evects of Instruction on Changes in Epistemological Beliefs [J]. Contemporary Educational Psychology, 2005, (30): 318–320.

[4] 喻平．教师的认识信念系统及其对教学的影响[J]．教师教育研究，2007，（4）：20-22．

[5] 张侨平，黄毅英，林智中．中国内地数学信念研究的综述[J]．数学教育学报，2009，18（6）：16-19．

[6] Hofer B K. Personal Epistemology Research: Implications for Learning and Teaching [J]. Journal of Educational Psychology Review, 2001, 13(4): 372.

[8] 康武．信念——数学教师的方向性问题[J]．数学教育学报，2003，12（2）：17-20．

[9] 张红．数学教学中的隐形课程及其开发[J]．数学教育学报，2008，17（4）：57-59．

[10] Lisa D Bendixen, Deanna C Rule. An Integrative Approach to Personal Epistemology: A Guiding Model [J]. Educational Psychologist, 2004, 39(1): 69–80.

[11] 周莹，唐剑岚，黄国稳．初中生数学认识信念的SEM研究[J]．数学教育学报，2007，16（2）：31-34．

[12] 肖春梅，喻平，颜丽增．高中生数学认识信念的现状及对学习的影响[J]．数学教育学报，2007，16（3)：40-43．

[13] 金美月，郭艳敏，代枫．数学教师信念研究综述[J]．数学教育学报，2009，18（1）：28-29．

[14] 杨豫晖．教师教学信念的检视与反思[J]．课程·教材·教法，2010，（12）：100-101．

[15] 童莉．数学教师专业发展的新视角[J]．数学教育学报，2010，19（2）：23-26．

[16] 李渺，宁连华．数学教学内容知识（MPCK）的构成成分表现形式及其意义[J]．数学教育学报，2011，20（2）：10-13．

[17] 张俊青，陈旭清．论数学地经验性本质[J]．数学教育学报，2010，19（1）：67-70．

Dimension Analysis and Orientation Research of Mathematics Teachers’ Epistemic Belief in Higher Vocational College

CHENG De-sheng1, YU Ping2
(1. Sub-branch of Nanjing, Jiangsu United Vocational and Technical College, Jiangsu Nanjing 210019, China; 2. Mathematics Science Institute of Nanjing Normal University, Jiangsu Nanjing 210097, China)

Using two dimension disposition scale of epistemic belief about mathematics pedagogy, Researching every dimension’modality of mathematics teachers’ mathematics pedagogy and the differences of epistemic belief between belief different teaching age period. Teachers’ understanding of 13 dimensions has Similar view, but differences obviously, and teachers’ understanding has divergent situation about the same dimension in same teaching age period. Mathematics teachers’ mathematical epistemic belief prefers to the traditional objectivist view, pedagogy epistemic belief prefers to the modern relativism teaching view. There is a certain degree of correlation in epistemic belief about mathematics pedagogy and teaching age.

higher vocational college; mathematics teacher; epistemic belief about mathematics teaching

G451

：A

：1004–9894（2015）02–0091–07

[责任编校：周学智]

2014–12–21

2012年度教育部人文社会科学研究一般项目——中小学教师认识信念取向及其对教学行为影响的研究（12YJA880153）；江苏省教育科学“十二五”规划课题——高职数学职业模块校本开发研究（D/2011/03/030）

程德胜（1970—），男，江苏南京人，副教授，主要从事数学课程与教学论、职业教育研究．