基于现代教学理念下课堂教学“留白”艺术的观察研究——以高中数学《随机事件的概率》和《割圆术》两堂课为例

马茂年，李 芳

（1．浙江省杭州第十四中学，浙江 杭州 310006；2．浙江省温州中学，浙江 温州 325014）

基于现代教学理念下课堂教学“留白”艺术的观察研究
——以高中数学《随机事件的概率》和《割圆术》两堂课为例

马茂年1，李 芳2

（1．浙江省杭州第十四中学，浙江 杭州 310006；2．浙江省温州中学，浙江 温州 325014）

教学中的“留白”，是教师用心灵在施教．著名教育家苏霍姆林斯基说过：“有经验的教师往往只是微微打开一扇通向一望无际的知识原野的窗子．”教学“留白”设计并不是对于部分知识的舍弃，而是通过空白的设计去调动学生思维的主动性与积极性，通过自己的探索研究去获得空白处的内容，从而达到对知识的掌握．以《随机事件的概率》和《割圆术》两堂课中不同教师课堂留白情况，通过对比分析运用课堂留白的误区和合理运用留白的策略，为评价教师的课堂留白行为和合理处理课堂留白提供一些借鉴．调查中发现高中数学课堂教学中留白主要存在以下几个问题：（1）课堂留白很少；（2）教师不知道如何合理运用课堂留白．结合分析的结果得到高中数学课堂中运用留白的策略：（1）要预设好留白时间；（2）在“主问题”上多花时间；（3）“主问题”留白要先作铺垫；（4）好的问题是留白的前提；（5）注重在时间和内容上留白；（6）注重在评价和情感上留白．

课堂教学；观察研究；课堂留白；艺术策略

1 问题提出

浙江省从2006年9月份开始进入教育课程改革，《全日制高中数学课程标准（实验稿）》中明确提出“教学要以学生为主体”，要求在数学教学活动中学生的认知发展水平和已有的知识经验基础上，教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会．这就要求教师在课堂中要充分发挥教师的引导作用，有意识地培养学生的思维能力，促进学生自主参与数学学习．

但是，在现有的高中数学课堂中，还是普遍存在教师讲得很多、很透、很实，甚至满堂灌的情况．这样导致了留给学生想象的余地很少，激不起学生对已有知识的思考和对更新知识的渴求，从而扼杀了学生的想象力和创造力．目前，对于教师课堂提问的研究很多，但多是针对教师提问的有效性进行的．对于教师提问后的课堂留白时间的系统的研究很少．然而，课堂留白是教学中培养学生独立思考的重要机会，是改变教师满堂灌现象的一个很好的手段．因此，数学教学要从传统的教法中走出来，改变数学等于枯燥的讲授、乏味的练习、生硬的教科书等的冰冷印象，必须注重课堂中教师留给学生自主思考的时间，即课堂留白的处理．

目前，高中数学课堂中的留白主要存在以下几个问题：

（1）课堂留白很少．

表现在教师还没等学生回答，就抢着告之正确答案；还有的老师甚至根本没有意识到要给学生思考的机会．教师的这些表现的原因主要有：① “赶进度”，怕教学内容无法按时完成，但教师“赶完进度”不代表学生跟上了进度；② 怕学生的错误解答或新奇的想法导致问题无法解决，主要的原因在于教师自身的数学素养不够，对课堂中设置的问题没有深入研究，只能应付课堂中的“预设”，无法有信心面对课堂中的“生成”．③ 急于展现自我的心理因素，经常在一堂精心准备的课里蕴藏着教师很多不错的想法，但基于自我展现的心理而抢夺学生的话语和思维权[1]．

（2）不知道如何合理运用课堂留白．

有些老师已经意识到课堂上要留一些时间给学生思考，在提问以后要有一定的候答时间，但是由于经验不足，往往达不到很好的效果．有些课堂虽然在表面上看留给了学生很大的思考空间，但对于简单的问题，学生可能一下子就可以得到正确答案，留白时间过长不仅影响了课堂进度还会会让学生失去兴趣；另一方面，对于难度过大的问题，教师不加点拨，便留了大量时间让学生独立作答，这对学生思维发展也是没有益处的，甚至会打击学生学习数学的信心[2]．

因此，对于数学课堂留白的研究不仅在理论上而且在实践上都是十分迫切的．

2 研究意义

新课改提出数学教育不能过分强调“三大能力”，应关注学生的一般能力，培养学生提出并解决实际问题的能力、数学思维的能力、创新能力和实践能力．随着改革的进一步推进，人们越来越意识到教学如何能做到“减负提效、培养能力”是这次改革成败的关键[3]．要解决好“减负提效”这个问题，首要一点就是要解决课堂提问的有效性，这也是“课堂留白”的研究所要分析的问题．

研究者认为：

其一，课堂留白有助于激发学生的主体意识．教师为学生留下自由驰骋的“空白”，学生可以在教师精心留取的“空白”中充分认识到“自我”的价值，将自己投入到课堂学习中，极大地激发和提升学生的主体意识．

其二，课堂留白有助于触发学生的学习内动力．人们新颖独特的见解常出现在思维过程的后半段．教学留白的过程是学生积极思维的过程，容易激发学生思维的火花，容易激发学生自主探究学习的兴趣，提高其发现问题、分析问题和解决问题的能力，有利于培养学生的创新意识、创新能力．

其三，课堂留白有助于学生形成各自的认知策略．同一问题，有的学生一看就知道正确的答案；有的学生要思考一段时间后找到正确的答案；还有一些学生百思不得其解．这就是认知策略的差异．在以传统的教师讲授为主的课堂教学模式中，学生只需被动地听从教师的讲解，很少主动地进行紧张的思考活动，有效的认知策略由于缺乏一定的训练难以形成．而留白，它为帮助学生遵循联想、组合、尝试、调整这样的思考过程，提供了时间的保证和实践的可能．长此以往，便会使他们逐步形成各自的认知策略．

同时，课堂是学生学习的主阵地，学生的成长依赖的是每一堂课的积累，提高课堂教学效率是课程改革的重中之重．课堂留白则是提高课堂效率的一个重要策略．即便是用相同的教材、相同的教案，不同的课堂留白时间、留白时机等则会带来迥异的课堂效果．对课堂留白策略的研究将对促进有效课堂教学有着十分积极的影响[4]．

课题主要研究的问题是：① 通过对大量的数学课的观察，分析目前高中数学课堂教学中，课堂留白的现状和所存在的问题．② 针对研究中发现的问题，提出课堂留白的对策，为改进教师的课堂留白行为，使课堂真正成为师生对话、交流与互动的平台提供参考．

3 概念界定

3.1 留 白

留白，作为中国画的一种表现手法．从绘画的角度讲，它是指在一般除主题、情节有关的必要点缀物或陪衬外，大多不画背景，不要任何多余的东西，在画面上留有较大的空白，是画家在创作过程中为了更充分地表现主旨而精心留出的“空白”．这种空白，并非空而无物，而是相对于物象的实所呈现出的艺术的虚，它是一种空灵，一种虚中求实，一种虚与实的和谐统一．它形成了一种节奏的变化，以给读者留有自由驰骋的余地，显示出美的意境[5]．

3.2 课堂留白

课堂留白，是指教师于一定的时空中，针对某一目标，有意留出相当的时间和空间让学生思考，向学生提供充分的从事数学活动的机会，让学生自己去构建对数学的理解．

留白的课堂教学，为学生提供充分的自主活动、自我表现和自我发展的机会．教师主要是引导学生根据现有知识去探根溯源，让学生在自主探究的过程中获得知识、巩固知识，更重要的是使学生学会如何获得这些新知识[6]．

4 课堂留白实例分析

4.1 研究方法设计

4.1.1 研究个案的选择

在选取个案时，考虑到可比性和典型性的问题，案例一被用来比较的两节课是2012年温州市优质课获得第一名的教师（下面用A表示）和另一位参赛教师（下面用B表示）的课．课题都是“割圆术——圆周率π的近似求法”，这是人教版必修三的课后阅读与思考内容．案例二被用来比较的两节课是2011年浙江省优质课的第一名（下面用C表示）和另一名参赛教师（下面用D表示）的课．课题都是“随机事件的概率”，这是人教版必修三的教学内容．选择的4位教师都是参加浙江省优质课的地区级代表选手，也可以在一定程度上代表一个地区或者一个学校的教学水平．从而增加案例的典型性和可比性．

4.1.2 研究数据的搜集

反复观看视频，将视频进行了多次整理．第一次整理：将整个教学过程用文本的形式记录下来，着重记录教学过程中学生和教师的对话、教学环节和师生活动；第二次整理：以表格的形式记录教师提问时间、学生反馈的起止时间以及教师留白时间；第三次整理：在前两次整理的基础上，添加教学环节中的细节，包括教师的行为、学生的反应等．

4.1.3 数据的编码

● 教师提问类型编码

根据教师提问的指向性明确与否，将教师的提问分为A和B两种类型，其中A代表有指向性，即学生能理解问题；B代表没有指向性，即学生不能理解问题．

根据提问的作用和目的，根据崔允漷主编的《课堂观察LICC模式》中的分类将教师的提问归为A、B、C、D四种类型，其中A表示复习性提问，即复习巩固提问；B表示启发性提问，即教师预设的启发性提问；C表示生成性提问，即由学生回答或反应引起的生成性提问；D表示评价性提问，即评价判断性提问．

● 教师留白时间编码

根据教师候答时间的长短，将留白时间分为A、B、C、D、E五种类型，其中A表示留白时间在3秒内，B表示4～10秒，C表示11～30秒，D表示31～60秒，E表示60秒以上．

● 学生回答类型编码

研究中将学生的回答情况归为A、B、C、D、E五种类型，A表示附和；B表示齐答都正确；C表示齐答不统一；D表示独答；E表示无人回答．

4.2 实例分析

4.2.1 案例一：割圆术

（1）观测点选择说明．

① 课堂的引入：课堂的引入部分引导学生建立通过估算单位圆的面积来估计圆周率的近似值，建立整堂课的初步的思路框架．

② 为何在求解正六边形面积后转而求解正十二边形面积：让学生体会正十二边形与正六边形面积之间的递推关系，由此得到计算正十二边形比其他正多边形更加有利．

③ 正2n边形与正n边形的边长之间的递推关系：正2n边形与正n边形的面积之间的递推关系的本质是边长之间的递推关系．

④ 圆周率近似值上限的估计：如何利用类似上面的方法得到圆周率上限的估计．

类比容易想到的方法与刘徽的割圆术：让学生体会刘徽的割圆术在减少计算量方面十分有效．

⑤ 初始值是否一定是正六边形：既是课堂总结，又是课堂教学效果的检验，让学生体会到割圆术的本质是利用了其中的递推关系，而非正六边形这个初始值．

（2）数据分析和结果．

① 从教师提问类型上看．

教师提问是数学课堂教学的有效方法，两堂课教师均采用提问的方式展开教学．区别在于课堂提问的数量和提问类型．从两堂课的统计结果来看，两位教师的提问指向性都比较明确．教师的提问次数有较大差异，教师A在课堂中提问22次，而教师B提问40次．教师的提问类型也有一些差异（如图1）．但从各种提问所占的比例上来看，“启发性提问”都占了很大比例，分别为63.6%和75%；“复习性提问”所占比重相当；“生成性提问”在教师B的提问中所占比例为20%大致为教师A（13.6%）的1.5倍；“评价性提问”在两位教师的提问中所占比例最少且B教师没有“评价性提问”．

图1 两位教师提问类型分布图

这两堂课很大的不同在于重难点的突破方式：A教师采取问题串的形式，逐步递进，引导学生探求加倍边数的方法与递推关系的发现；B教师采取完全让学生阅读课本自学．

这里着重以如何得到加倍正多边形的方法与如何发现正2n边形面积与正n边形面积的递推关系来收集留白数据．

首先通过对录像时间点分析，获得两节课的两个关键环节的时间分布（见表1）．

② 从关键性问题所占时间上来看．

然后综合学生的理解来达到同样的教学目的．

表1 关键性问题留白时间统计表（时间单位：秒）

通过表格发现两节课对于本节课的重难点的突破所运用的时间分别为2 082秒和1 682秒，相差并非很大．

其次对关键两个环节中两节课的留白时间予以统计，分别为447秒和667秒，可见教师B在该环节上明显比教师A留给了学生更多的思考时间．从留白时间所占比例来看（如图2），教师B的留白时间占总时间的比例（21.5%）几乎是教师A（39.7%）的两倍．

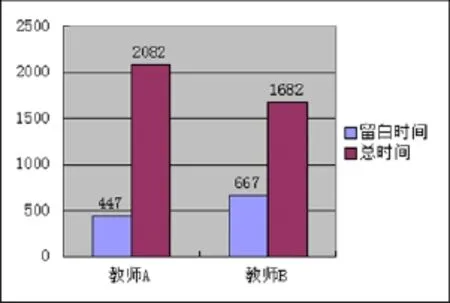
图2 留白时间占环节总时间分布图

最后统计了两节课课堂留白的总时间以及占整节课的比例，两位教师的课堂留白时间分别为540秒和984秒，所占比例分别为20.8%和39.1%，可见教师B的留白比教师A明显要多．但是从关键性问题留白时间所占总留白时间的比例（如图3）来看，教师A所占比例（82.8%）明显比教师B（67.8%）大．

③ 从学生回答类型看．

从统计结果（如图4）上看，两堂课中学生“独答”的形式占了较大比重，说明教师在处理学生回答方式上差异不大，多采用个别回答的形式．而教师A的课堂中“齐答”（包括“齐答都统一”和“齐答不统一”）所占比例（31.8%）比教师B（20.0%)要大得多，说明教师A的课堂气氛相对教师B的课堂气氛活跃．另外，教师B的课堂中出现无人回答的比例达到了22.5%是教师A（9.1%）的两倍多，这说明教师B的课堂中学生的思维并不活跃，甚至一度处于停滞状态．

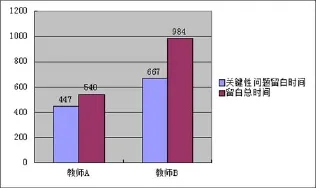
图3 关键性问题占留白总时间分布图

图4 学生回答类型分布图

④ 结论与启示．

从课程录像中可以发现，两位教师在教学基本功上都十分扎实：教态自然得体，板书规范，表达清晰，语言简练流畅、轻松幽默，亲和力强，并会合理地运用肢体语言．提问的类型上差异不大，主要的教学差异就在于如何处理课堂留白与教师引导之间的矛盾．

统计结果显示，教师A和教师B留给学生思考的比率分别为21%和40%，可见，教师B给予了大量的课堂留白时间，旨在培养学生自主思考发现问题的能力；而教师A的留白时间相对较少．从学生回答情况可以看出，一味多的留白，并不能真正达到培养学生思维能力的效果．虽然教师B给予学生较多的思考时间（即使在学生回答情况不佳时），但是由于学生的知识储备与思维能力有限，在缺乏一定的引导下，学生很难做到自行发现问题，这导致课堂气氛不活跃，学生思维停滞，被老师牵着鼻子走；而教师A虽然总体课堂留白时间相对较少，但是对于需要突破的教学重难点，都做好了一定的引导，设置了一系列的问题串，在关键性问题上给予了较多留白时间．教师A对于课堂留白的正确处理，才真正起到了活跃课堂气氛，发展学生思维能力的作用．虽然也出现了极少的无人回答的情况，但教师都及时加以引导，使学生通过思考能够自己获得问题的解答．

所谓教师的引导，通常总是以问题的形式出现，好的问题指向性明确，难度适中，并带有一定的启发性，能够使得学生更加容易找到正确的思路；质量不佳的问题指向性不明确，要么难度太低，没有启发性；要么难度太高，学生不知所措．课堂留白的目的是给予学生思考的时间，特别是有意义的思考时间——即学生遵循正确的思路，通过思考获得某一阶段的成果，然后再经过进一步的引导与思考获得最终答案[7]．因此好的问题，是留白的前提，只有提出了高质量的具有引导性作用的问题，才能将学生引入正确的思路，从而才能让学生在留白的时间中获得成果；否则，在缺乏必要的引导时，许多学生一头雾水，不知所措，那么即使教师留给再多的思考时间，对于学生也只是望洋兴叹罢了[8]．

4.2.2 案例二：随机事件的概率

（1）观测点选点说明．

① 随机事件的概念的形成是本节第一个重点，如何让学生形成概念中“在条件S下”这一前提是这个问题的难点；

② 为什么选正面和反面的可能性大小一样？

③ 大家所得的试验结果并不一致，这是为什么？

④ 为什么要把小组还有全部的数据加起来，这样做的目的是什么？

⑤ 通过试验发现什么现象？

⑥ 如何定义随机事件的概率？

⑦ 频率和概率的区别和联系在哪里？

（2）数据分析与结论．

① 从教师提问类型上看．

从两堂课的统计结果来看，两位教师的提问指向性都比较明确．教师的提问次数差异不大，分别为54次和48次．教师的提问类型存在一些差异（如图5）．但从各种提问所占的比例上来看，“复习性提问”在教师C的提问中所占比例为35.2%，占了较大比重，大致为教师D（22.9%）的1.5倍；“启发性提问”在教师D的提问中所占比例为60.4%大致为教师C（38.8%）的1.5倍；“生成性提问”在教师C的提问中所占比例为25.9%大致为教师D（12.5%）的2倍；“评价性提问”在两位教师的提问中所占比例最少且C教师没有“评价性提问”．可见两位教师都比较注重启发性提问和复习性提问的运用，但教师D主要以启发性提问为主，而少有生成性提问．

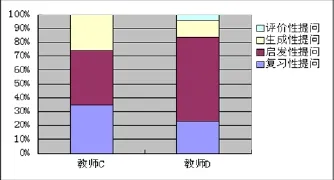
图5 两位教师提问类型分布图

② 从关键性问题所占时间上来看．

两节课的整体设计类似，主体环节都是从生活中的随机事件引入→通过问题辨析完善概念→进而过渡到如何研究随机事件的概率→接着通过硬币试验发现规律“随着试验次数的增加频率稳定于概率”→最终得到随机事件概率的定义，进而辨明概率与频率的区别与联系→提出小概率事件等概念→应用→总结．其中关键的问题有随机事件的概念，随机事件的概率的概念，概率和频率的区别和联系等．

首先通过对录像时间点分析，获得两节课的几个环节的时间分布（见表2）．

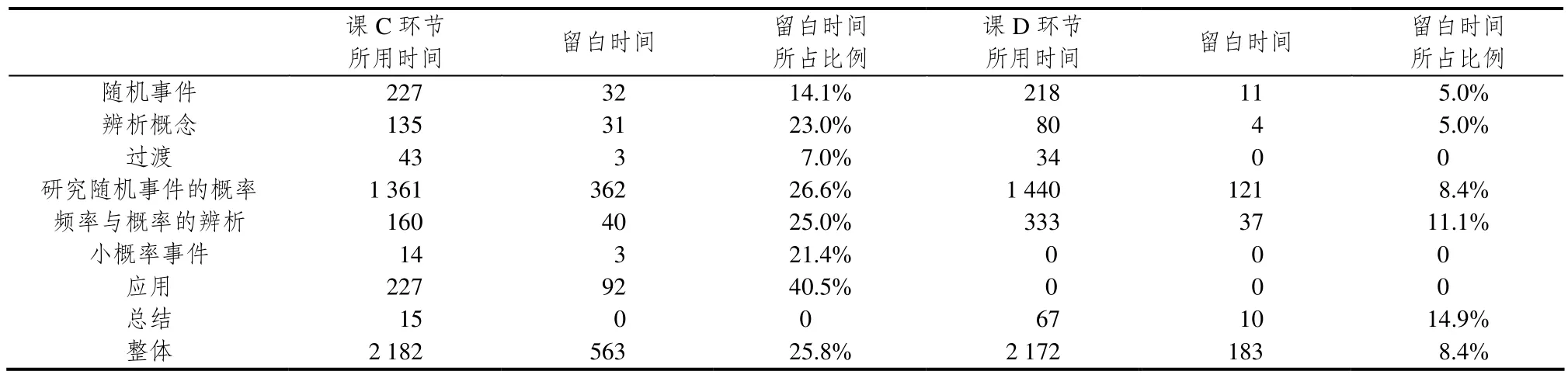
表2 随机事件的概率课堂留白时间统计表（时间单位：秒）

通过表格发现两节课整体的时间分布接近，随机事件概念的讲解课C用了227秒，课D用了218秒，在核心的研究随机事件的概率的环节课C用了1 361秒，课D用了1 440秒．课C比课D多了一个应用环节227秒，课D比课C多了一个总结的环节67秒，在时间的衔接上课C显得更为紧凑，师生交流时间相对多一点．

其次，对两节课的留白时间予以统计，课C与课D分别为563秒和183秒，整整多出了380秒，在关键的研究随机事件概率的环节中分别为362秒和121秒，可见教师C在该环节上明显比教师D留给了学生更多的思考时间．从关键问题留白时间所占整体留白时间的比例来看（如图6），教师C的关键性问题留白时间占总留白时间的比例（25.8%）几乎是教师D（8.4%）的3倍．

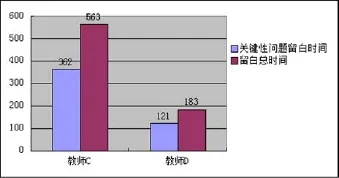
图6 关键性问题留白时间占留白总时间分布图

通过分析，发现课C几乎在每个环节课堂留白时间都要比课D要多，课C没有进行常规的总结，而是用张景中院士的话收尾，课D则是让学生总结．在整个师生交流的环节，课C的教师问题显得更简洁紧凑，给了学生更多的思考时间，课D的教师问题相对的显得啰嗦，对于同一个知识点用几个例子来提问，并且有些关键性的点都采用了自问自答的形式，课堂虽然声音不断，但是教师的声音为主．

③ 从学生回答类型看．

从统计结果（图7）上看，教师C的课堂中“独答”所占比例（37.0%）比教师D（20.8%）要大得多，说明教师C相对教师D的对于学生的主体地位更加关注，学生的思维层次要求更高．另外，课D课堂中“齐答”（包括“齐答都统一”和“齐答不统一”）所占比例（68.9%）比教师C（44.0%)要大得多，从学生的表现感觉更多的是一种附和，并没有真正做到以学生为本，而只是牵着学生走．

图7 学生回答类型分布图

④ 结论与启示．

分析发现，课C教师和课D教师留给学生思考的比率分别为21%和5%，这反映出C教师对迁移性、复杂性和创造性问题等待的时间明显较长，体现出具有高效地激活学生主体性和适度控制教学情境的能力．从课堂观察中明显发现课C教师在数学课堂上提问后，会做必要的时间等待，然后指定学生回答，有时学生还会主动举手发言或提出更好的想法，课堂气氛较活跃．相比之下，课D教师在课堂的控制上显得耐心不足，等待时间稍微长一些，就急于提示，甚至替代学生回答，而且对学生回答缺乏必要的引导和反馈，有明显的“强加”、“灌输”的感觉，课堂气氛较沉闷．

在所使用的教学任务上，两位教师在课堂中采用的教学任务的类型上表现出不同的特点．经统计，课C教师约有563秒的时间用于学生的主体性活动，并且在每一个环节都有20%以上的占比时间，主要包括回答复杂性提问以及学生按教师要求动手操作、讨论等有较长时间思考的自主活动；而课D教师仅有183秒，有些环节留白的时间5%不到（见表2）．这些数据较好地反映出两位教师在教学任务的运用上存在明显差异，课C教师与课D教师相比，倾向于使用探究型或解释型的教学任务，教学中通过探究使学生参与到教学活动中，获得数学活动的经验，建构对知识的理解，其目的在于通过数学活动促进学生对知识的理解．而课D教师在记忆型和解释型任务的设置方而明显地高于课C教师，教学侧重点在于对问题的剖析，教学目的主要是为了帮助学生加深对知识的记忆，或向学生提供知识的介理解释，以期帮助学生在理解的基础上对知识进行记忆．

对两位教师数学课堂教学行为的比较分析表明：课C教师注重突出学生的主体活动，丰富学生的数学活动经验；善于提出富有层次的、能激活学生思维深层参与的启发性问题；灵活调控课堂教学，并做必要的时间等待是课C教师教学机智和教学智慧的体现．

5 课堂留白策略

强调课堂留白并不是局限于对留白时间长度的追求，还有许多内在的诉求．根据上述对课例的研究和分析，这一部分将针对在实践课堂留白时存在的问题，提出正确处理课堂留白的对策．以期给教师有意识地运用留白以参考，真正起到“于无声处听惊雷”的效果，以更好地平衡教学中学生主体和教师主导的关系．

运用课堂留白应注意以下几个方面：

5.1 要预设好留白时间

美国有位教育专家也说过，对学生的提问，在每个问题提出之后，至少要等待3秒钟，这样做有很多好处．这句话强调了课堂留白的重要性，也给出了课堂留白时间的参考数值．但是由于课堂的复杂性，课型、知识的难易程度以及学生对知识掌握水平等的不同，很难给出一个处理留白时间的定量结果．正由于对留白时间的长度的把握并不是胡子眉毛一把抓的事情，教师在备课的过程中应当针对课型、重难点、学生预期的反映等等因素预设好课堂留白的时间[9]．

通过研究发现，在概念的教学中适当地留出10—15秒的时间让学生充分理解概念对于学生对概念的掌握是十分有效的；另外，在练习时根据练习的难易程度，给足学生15—60秒的思考时间是必要的；探究所需的留白时间就更长了，研究发现针对探究的问题留白的时间达到180秒以上的课，探究效果更为显著，学生积极性和求知欲也更高……当然，在具体实践中，留白时间是可以而且应当是灵活变通的，这也给教师提出了更高的要求．

5.2 在“主问题”上多花时间

所谓“主问题”就是教学中教师为了突破教学的重难点，更好地达到教学目标所提出的问题．经常出现这样的课堂，教师过分追求留白，在每个问题提出后都给了学生一些时间去思考，而一堂课的时间是有限的，而且并不是每个问题都需要过多的思考，这样的课堂留白时间虽长但没有针对性，以致使教学失去连贯性，影响了教学的进度[10]．因此，课堂留白应注意留白时机的把握，用有限的时间达到最好的留白效果，不妨在“主问题”上多花时间，而不过分追求留白的长度在一些本不需要过多思考的问题上浪费时间．

研究者在一次丽水地区的研讨活动中，就同一个课题——《数列的递推公式》上了两堂研讨课，但两次课的教学效果迥异．差异就在于，第二次授课时吸取了第一次的经验，针对那堂课的教学目标和要求，在保证课程进度的前提下对一些次要问题的留白时间进行压缩，在“主问题”上适当延长了留白的时间．给“足”学生对于“主问题”的思考时间，学生探究的目标和方向更明确了，学习效果和知识的把握也更加到位和准确．

5.3 “主问题”留白需先作铺垫

学生的最近发展区在哪里？教师要尊重学生的差异性，像中医号脉一样，不断“摸索”．既然主问题是重难点所在，对于学生学习来说必定存在一定的困难，教师若在直接抛出问题后，便留出了大量的时间让学生自主探索，那样虽然表面上在“主问题”上花了大量的时间，但事实上只是一些不必要的浪费，使课堂陷入冷场的尴尬境地[11]．因此，教师要充分了解学生，在学生知识出现空白或者思维陷入困境的时候，给予适当指导．教师可以针对“主问题”设计阶梯状的“问题串”作为铺垫，再留时间让学生思考．

比如在《平面》一课中，针对“平面”概念的学习，一位老师直接提出问题“同学们，你们知道什么是平面吗？”另一位老师则是设计了7个分解问题：① 一个点朝两头无限运动，形成什么图形？② 一条直线朝一个方向运动，形成什么图形？③ 将钢丝（作为直线）在空中平动了一圈，这样形成什么了呢？④ 试举出身体具有“平面”形象的事物．⑤ 你对平面的感受是什么？⑥ 在自然界中存在真正的平面吗？⑦ 无限延展的平面如何表示？这两位老师表面上对于“主问题”——“什么是平面”的留白时间相差不大，但课堂实践效果表明后者“先作铺垫”的设计，切住了学生的最近发展区，让“主问题”的讨论步步逼近，理解层层加深，这样的留白处理显得更加合理．

5.4 好的问题是留白的前提

课堂留白是为了提供学生更多的思考空间，培养学生的思维能力，但如果所提问题本身没有价值，一味的留白也是无所裨益的．有些教师对“课堂留白”的实质理解不够，认为只要留给学生思考的空间就能发挥留白的积极作用．殊不知，在教学活动中所提的问题没有价值，探讨便流于形式，留白的运用也只是空谈罢了．因此要真正发挥留白的作用，提“好”的问题是前提．

比如《等差数列的前n项和》一课中，多数学生对于高斯用“首尾相加法”计算1到100的和的故事都已耳熟能详，若还纠结于对1到100的和的求法的探究，是不利于对本节课的教学目标——让学生学会用“倒序相加法”来求等差数列的前n项和的把握的．既然首尾相加简单易行，还有学习“倒序相加法”的必要吗？仔细理解分析后，可以发现：“首尾相加法”在项数为偶数的等差数列求和中较为方便，而“倒序相加法”对于项数的奇偶没有要求．于是便有了一个“好”问题——探究求1+2+3+…+99的方法．在简单叙述完高斯的故事后，留时间让学生探究求1+2+3+…+99的方法，才能更好地突破重难点，使学生体会并把握“倒序相加法”的思想，达到教学目的．

5.5 注重在时间和内容上留白

首先，教师在向学生提出问题后“留白”．科学家克莱因曾极力提倡：留给学生自由活动的时空，他获得的就不仅仅是一个问题的解决、一种方法的掌握，而是一个人从整体意义上对科学活动的领悟．从本质上说，这种“领悟”离不开积极意义的探究空间和时间．而不少教师在教学中，提问后就急着让学生举手发言，结果很少有学生能回答到点子上，究其原因，是学生缺乏思考时间．另外，问题阐释后还要给学生“留白”．教师在课堂上张弛有度，让人感觉有节奏，在分析一道题或一个小结内容完成后，应留点时间让学生静静地想一想，梳理一下思路，记录下重要的知识，看看来时的路，望望前方．这也是对学生思考问题、处理问题能力和良好学习习惯的培养．只有当学生真正悟到些什么时，教师的教学才是有效的．再者，若在课堂结尾处“留白”，弹好“终曲”，则会激发学生进一步探究的兴趣，并获得“言犹尽而意无穷”的效果．教师要舍得花一些时间让学生进行反思自问：今天主要讲了什么内容？知道了多少（整理内化）？还有哪些不懂的地方（确定补缺方向）？对教材中哪些地方还存在疑问（提高质疑能力）？这样以“不全”求“全”，在有限中求无限，就为一堂好课的结尾注入浓郁的色彩和艺术的含蓄，给学生以想象和回味的空间[12]．

教师在课堂上处理重难点内容时，自己不直接详细讲解，而是精心设计问题让学生自己去探究，合作学习，直到解决问题，这也可认为是教学的“留白”．苏霍姆林斯基曾说过：“有经验的教师往往只是微微打开一扇通向一望无际的知识原野的窗子．”教师在设计问题，制造悬念后留白，可以激发学生的学习兴趣和强烈的求知欲，它具有含而不露、开而不达的特点，给学生们留下足够的空白去思考、去探索，从而加深对知识的理解和掌握，起到“欲擒故纵”的教学效果．另外，当面对容量大、课时紧张的新课程时，教师要在把握主干知识的前提下对教材内容进行梳理整合，提高教学效益，这也是教学“留白”．

5.5 注重在评价和情感上留白

实行延迟性、暂时性的不评价，即把学生的自评与互评权还给学生．教师在有思考价值、有争议的问题上，不要直截了当地对学生的回答做出“对”与“错”的评判，而将评价的时间推迟，给其他学生发表意见的机会，给学生一个自由思考的空间，让学生在和谐的气氛中驰骋想象，畅所欲言，相互启发．从而使学生获得更多、更美好的创新灵感，使个性思维得到充分的发展．如果教师对学生在教学过程中所提出的新颖但不成熟的认识立即给出评定，常常会对学生的思维能力，尤其是发散思维能力产生抑制作用．所以，一堂课中对学生的信息反馈，并非一律都得“及时”评价，有时候“及时”评价反而会扼杀学生创新意识和创新能力的发展．把学生的自评与互评权还给学生，有时还会收到意想不到的效果．实践证明，学生们在评价同学的同时，自己也会加深认识，甚至是对问题的理解上升一个层次，从而提高学生的比较和分析能力．同时，学生的思维能力和语言表达能力也能得到相应提高．而且，学生在互相评价时往往是站在同一个高度来看问题，这样更直接，也更容易被学生所接受，自信心也就有了．当然伙伴的肯定更是激发了他们探索的欲望，点燃了他们智慧的火花[13]．

教师应尽可能地为自己的情感体验留白，营造良好的氛围，激发学生的学习情感，促使学生自己去体验情感、积极探究，并在学生研讨时起到穿针引线的作用，使问题的研究不断深入，层层推进，直至达到研究目标．现代认知心理学的研究表明，认知与情感是紧密联系的，作为非认知因素的情感在学习活动中主要起动力作用，承担着学习的定向、维持和调节等任务．因此，关注学生的学习情感是非常必要的．而课堂学习是一个情感体验的过程，在这个过程中，教师应该以富有情感的方式教，学生才会以富有情感的方式学，但教师的情感体验不能代替学生的情感体验，教师应留出自己情感体验的空白．如在课堂的合作学习活动中，教师不必去指定合作小组的组长、发言人名单，而由学生自己去把握、去产生．

6 思考与展望

6.1 思 考

课程改革对数学课堂以及教师都提出了新的要求，课堂留白是课程改革的一个不容忽视的重要方面，因此，选择这个角度进行了研究．

研究通过文献梳理，分析了当前数学课堂中留白的研究进展，发现这方面的理论和实践研究都非常欠缺．通过对数学课堂现状的调查发现，教师在处理课堂留白时存在很大的问题．主要表现在：首先，许多教师还没有很好地理解课程改革的理念，没有变更传统的教学模式，课堂留白很少，学生缺乏独立思考的空间；其次，有的教师已经意识到课堂留白的重要性，但是无法正确处理课堂留白与教师引导的关系．

针对这些问题，课题通过大量的课堂观察和实践，着重分析了《随机事件的概率》以及《割圆术》这两堂课的4位教师的教师活动，重点记录了教师提问、学生反馈以及教师的留白时间，并对教师的提问以及学生的回答情况进行了合理的分类．通过教师行为的对比以及数据的分析，得出了教师运用课堂留白时所存在问题的原因和较为合理的运用课堂留白手段，为如何评价教师的课堂留白行为提供了一些借鉴．在此基础上，提出了合理运用课堂留白的策略：（1）要预设好留白时间；（2）在“主问题”上多花时间；（3）“主问题”留白要先作铺垫；（4）好的问题是留白的前提．

6.2 展 望

研究虽然进行了大量的课堂观察和视频分析，得出了一些结论．但是由于时间和研究水平的限制，还有许多问题没有解决：（1）在课堂中如何区分课堂留白的合理性，怎样的课堂留白对学生是有益的；（2）如何提高教师运用课堂留白的能力；（3）针对不同的课，课堂留白时间多少比较适宜，留白的长度与课堂的质量存在怎样的联系；（4）进一步的后续跟踪，用学生的评价来说明教师正确的课堂留白行为与学生学习的关系．

在新课程理念下，要用一种发展的眼光看待教学，在进行教学设计时，要适当“留白”，随时调整，随时补充．不要把学生限制在教师的教学设计中，要关注学生的情感体验和创新品质，呵护师生交往互动过程中产生的智慧火花．这样，就能处理好课堂上生成的问题．

希望“留白”给学生自我发展开辟一条道路．教学中的“留白”，表面上看是教师的“启而不发”，是教师的教学艺术，实质上，是教师为学生的自我发展预留了一条宽阔的道路．教学的根本目的是促进学生的发展，而给学生的学习留下来空白，促成其主动学习，其效果是不言而喻的．

希望“留白”为学生自主探究留一片蓝天．探究学习是自主学习的最高层次，在探究学习中，学生主动性的发挥，学生已有经验的唤醒，学生搜集利用信息能力的应用等都有较高水平的发挥．引领学生自主探究的根本策略就是“引而不发，跃如也”，目标、情境、工具都为你准备妥当，就需要你自己去实践．这种策略如同教学中的“留白”，没有一点空白的教学是不会培养学生的探究精神和创造能力的．

希望“留白”为教学资源的生成留一个空间．课堂上的生成是师生的“即席创造”，是“无法预约的美丽”，是最宝贵的．教学中的“留白”正是“预约”这种“美丽”的捷径．教师依据学生在课堂活动中的状态，包括他们的学习兴趣、积极性、注意力、学习方法与思维方式、合作能力与质量、发表的意见建议、可能提出的问题与争论乃至错误的回答，等等，这些都是教学过程中的生成性资源，教师就会有意识地在某些地方或某些环节形成“留白”的方案，并预设好当生长点出现时应对的措施，从而给学生留下自主体会和悟解的空间，为课堂动态生成创造了条件[14]．

[1] 喻平，张英伯，曹一鸣．数学教学心理学[M]．北京：北京师范大学出版社，2010．

[2] 涂荣豹，宁连华，徐伯华，等．中学数学教学案例研究[M]．北京：北京师范大学出版社，2011．

[3] 蔡亲鹏，陈建花．数学教育学[M]．杭州：浙江大学出版社，2008．

[4] 曹一鸣．数学教学论[M]．北京：高等教育出版社，2008．

[5] 必凯，郑庭曜，孙伟，等．美国现代数学教育改革[M]．北京：人民教育出版社，2010．

[6] 黄荣金，李业平，顾泠沅．数学课堂教学研究[M]．上海：上海教育出版社，2010．

[7] 鲍建生，周超，顾泠沅．数学教育研究基础丛书•数学学习的心理基础与过程[M]．上海：上海教育出版社，2009．

[8] 张厚粲，徐建平．现代心理与教育统计学[M]．北京：北京师范大学出版，2009．

[9] 崔允漷，吴江林，林荣凑，等．课堂观察LICC模式课例集[M]．上海：华东师范大学出版社，2013．

[10] 叶立军，李燕．基于录像分析背景下的初中统计课堂教学提问研究[J]．数学教育学报，2011，20（5）：52-54．

[11] 白改平，韩龙淑．专家型—熟手型数学教师课堂提问能力的个案比较研究[J]．数学教育学报，2011，20（4）：16-19．

[12] 马茂年．快乐教学 改善心育 领悟本质——从“教书匠”走向“名教师”[J]．中学教研（数学），2013，（7）：4-7．

[13] 陈月兰．中日三角比内容比较——以上海教育出版社和数研出版社出版的教科书为例[J]．数学教育学报，2013，22（6）：60-61．

[14] 马茂年，俞昕．课堂教学回归“数学化”的讨论和分析——以高中“数学归纳法”的教学为例[J]．数学教育学报，2013，22（6）：83-84．

Research on the Art of “Blank Keeping” in Classroom Teaching Based on the Modern Teaching Theory——Taking Two High School Mathematical Classes “The Probability of Random Events” and “The Strategy of Cutting Circle” for Example

MA Mao-nian1, LI Fang2
(1. Zhejiang Hangzhou No. 14 High School, Zhejiang Hangzhou 310006, China; 2. Zhejiang Wenzhou High School, Zhejiang Wenzhou 325014, China)

The art of “blank keeping” in teaching requires teacher’s heart devoted. Suhomlinski famous Soviet educator said:“Experienced teachers are often only slightly open a window leads to the vast expanse of knowledge.” The design of “blank keeping” in teaching doesn’t abandon parts of the knowledge, while it can mobilize the students thinking initiative and enthusiasm. They will master knowledge through their own exploration and research. The author entered two classes---- “the probability of random events” and “the strategy of cutting circle” to study the two teachers’ behaviors on “blank keeping”. Compared the two teachers’ “blank keeping” strategies, this paper offers some advices on the evaluation of teachers’ “blank keeping” behavior in class and the reasonable treatment. The survey found several major problems of “blank keeping” strategy in high school mathematics teaching: (1) classroom blank rarely; (2) teachers do not know how to properly use the classroom blank. Combined analysis of the results, this paper obtained blank keeping strategies in high school mathematical classes: (1) To preset a good blank time; (2) to spend more time in the “main issue”; (3) get prepared for the blank of “main problem”; (4) good question is left blank on the premise; (5) focus on the timing and content of blank keeping; (6) focus on blank keeping on evaluation and emotion.

class teaching; observational study; blank keeping in class; arts strategy

G420

：A

：1004–9894（2015）02–0075–08

[责任编校：周学智]

2014–11–10

2011年度教育部人文社会科学研究规划基金项目——教师课堂行为研究（11YJA880139）

马茂年（1963—），男，浙江东阳人，特级教师，主要从事数学教育、教学，数学哲学与数学方法论、初等数学研究．