数学概念二次教学的实践与思考——以一道例题的教学为例

梁 栋，朱鸿玲

（1．天津杨村第一中学，天津 301700；2．天津师范大学 教师教育学院，天津 300387）

数学概念二次教学的实践与思考
——以一道例题的教学为例

梁 栋1，朱鸿玲2

（1．天津杨村第一中学，天津 301700；2．天津师范大学 教师教育学院，天津 300387）

数学概念二次教学是例题教学的一个环节，具有发现解题方法源泉和展现数学文化价值的作用．熟悉知识之间的内在联系是概念二次教学的起点，挖掘概念蕴含的数学思想方法是实施概念二次教学的途径，宽阔的教学视野是概念二次教学创新发展的基础，创造性的教学设计是概念二次教学的成败关键．

概念二次教学；数学思想方法；数学文化；思维

1 引 言

随着数学教育的发展，数学的教育功能越来越被人们所认识：学习数学不仅是为了让学生掌握一种重要的“工具”或“方法”，更重要的是掌握一种崭新的思维模式，即“会用数学的方式进行理性的思维”；同时也是为了培养学生的一种良好的素养，即“数学素养”．《数学课程标准（2011年版）》中指出：“数学为其它科学提供了语言、思想和方法，是一切重大技术发展的基础，数学在提高人的推理能力、抽象能力、想象力和创造力等方面有着独特的作用，数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分．”[1]

所谓数学思想，是指现实世界的空间形式和数量关系反映到人们的意识之中，经过思维活动而产生的结果．数学思想是对数学事实与理论经过概括后产生的本质认识，基本数学思想则是体现或应该体现于基础数学中的具有奠基性、总结性和最广泛应用性的数学思想，它含有传统数学思想的精华和现代数学思想的基本特征，并且是历史地发展着的[2]．

所谓数学方法，是处理、探索、解决问题，实施有关“数学廖想”的技术手段和操作程式．“方法”是指向“实践”的，是理论用于实践的中介，数学方法的运用、实施与数学思想的概括、提炼，是并行不悖、相互为用、互为表里的．由于数学方法与数学思想互为表里，它们都建立在一定的知识基础上，反过来又促进知识的深化和向能力的转化[3]．从数学方法论的角度考虑这种既统一又有差异，但却没有明确界限的数学思想和数学方法及其关系时，特别是考虑到中学生的实际认识水平，因而在教学大纲、教科书和实际教学中，通常把“数学思想”和“数学方法”笼统地称为“数学思想和方法”或“数学思想方法”．数学思想方法是数学的灵魂，是开启数学知识宝库的金钥匙，是层出不穷的数学发现的源泉．学生只有把数学知识上升到数学思想方法，才能有效地提高数学素养，乃至学生的整体素质．首先，数学思想方法是素质教育的重要内容．素质教育要求我们教育要面向全体学生，让每位学生都得到全面发展．为了实现“人人学有价值的数学，人们都能获得必需的数学，不同的人在数学上得到不同的发展．”[4]数学思想方法比形式化的数学知识更具有普遍性，在学生未来的工作和生活中有更加广泛的应用．其次，数学思想方法有助于教师正确地把握教材．高中数学教学体系包括两条主线：一是数学知识，这是写在教材上的明线；二是数学思想和方法，是隐含在数学知识中的暗线．教师只有掌握数学的思想和方法，才能明确领会教材编写的意图．才能从整体上、本质上去理解教材，才能科学、灵活地设计教学过程，选择教学方法，提高教学效率．再有，数学思想方法有助于帮助学生建立完善的认知结构、指导学生进行知识的正迁移、促进学生的思维发展，最终提高学生解决问题的能力．

但从目前高中数学教学现状来看，教学中对数学思想方法的重视程度还远远不够，数学教学以概念、定理、规律的灌输和大量的习题训练为主要的教学模式仍然占据着课堂教学的主要位置．数学是作为人类文化遗产中的一个主要部分，它来源于人又服务于人，因而是一门人类科学．而在数学学习被降为记忆公式和概念时，这一特别的文化价值就丧失殆尽了[5]．

为了克服传统数学教学的弊端，在高中数学教学中探索如何应用数学思想方法进行概念教学正日益受到国内外学者的广泛重视．发挥数学思想方法教学的特点和优势，探寻数学思想方法教学的途径和方法是数学教学应对当前普通高中课程改革的重要途径之一．

2 何谓“数学概念的二次教学”

目前，中国高中数学教学多采用“概念—例题—练习”的教学模式，在这一模式中，概念教学基本上是一次性的，即教师对新概念的教学设计投入精力较多，在随后的解题活动中只是对学过的概念复习巩固，极少进行二次开发．

概念是思维的基本形式，数学概念是数学思维的核心和逻辑起点[6]，是数学定理、性质的逻辑基础．因此很多概念都蕴含着丰富的数学思想方法．随着课程改革的不断深入，人们对概念教学的重视正逐渐从形式走向内涵，教学中，教师在让学生了解概念产生的背景，体验概念形成与发展的过程，感受概念中数学文化的同时，对概念中的数学思想方法也倾注了极大的热情，并在实践中积累了大量的宝贵经验，探索出许多行之有效的教学方法．然而，由于教学内容的制约，当概念中蕴含的数学思想方法与当堂教学内容无关时，这些“弦外之音”就容易被忽略，甚至是被埋没．而一旦用到这些数学思想方法，教师又往往将其作为一种解题技巧向学生介绍，无形中为数学方法蒙上了一层神秘的色彩，使学生匪夷所思，心生畏惧．概念中的数学思想方法让学生感到亲切自然，容易接受，也乐于接受，因此，概念教学不应是一次性的，应根据需要进行二次开发，并贯穿整个高中数学教学，让学生在概念中感受数学的思维方式，学习数学的思想方法．

数学概念的二次教学，是指教师引导学生对已掌握概念的再次学习，其目的不是复习巩固概念，不是进一步理解概念的本质，而是挖掘概念中蕴含的数学思想方法，并运用这些思想方法解决相关的数学问题．概念二次教学一般是在学习解题方法，探究解题方法得来的过程时进行，是例题教学的一个重要环节．

3 案例分析

下面是关于一道例题的教学案例，课型是高三复习课．

例1 设等差数列{an}的前n项和为Sn，若S4≥10，S5≤15，则a4的最大值为_________．（2008年四川高考题）

大部分学生不假思索就写出了如下解题过程：

设等差数列{an}的公差为d，

学生解答这两道题的思路是，先求出a1和d的取值范围，再求a4=a1+3d的范围，从而得到a4的最值．这种看起来顺理成章的解法实际上是错误的，例1由于a1≥1和d≤1的不等号方向相反而没能使错误成为事实，例2给了学生犯错误的机会，也就将问题暴露了出来．当教师提醒学生求出a4取得最值时相应的a1和d时，学生发现，当a4=-11时，有a1=1，d=-4，不适合已知条件，也就是说-11不是a4的最小值；当a4=12时，有a1=9，d=1，也不适合已知条件，即12不是a4的最大值（只有少数学生能自己进行验证，从而对解法提出质疑）．

教师分析上述解法错误的原因．以例2为例，已知条件中a1和d有制约关系，而解法并没考虑到这种制约关系，虽然a1和d的范围是由已知条件推出，但在求a4取值范围时，a1和d 却相对独立，这是错误的根源所在．这就如同由x2+y2=1可得|x|≤1，|y|≤1，但当|x|=1且|y|=1时，x2+y2=1显然不成立．错因已经明了，例1又尚未找到解决的方法，那么这两道题应如何解决呢？此时学生对正确解法充满期待，教师抓住时机就例1给出两个提示：

提示1：如果设a1=x ，d=y ，你有什么发现？

问题看似顺利解决了，但有学生追问：提示2是怎么想到的？这种方法为什么就一定正确？很多学生也有同感．

面对学生的追问，教师不直接回答，而是提出了新的问题：谁能告诉我，基底是怎样定义的？这个问题学生感到意外，努力回忆几分钟，除了个别学生能说出个大概，其他学生都忙着去翻课本．基底的概念在高中数学中出现的频率很低，只是在引入平面向量的坐标形式时做了一点贡献，以后便销声匿迹，因此很多学生脑海中没留下什么印象．这种情形在教师的预料之中，教师和学生一起再次学习基底的概念．

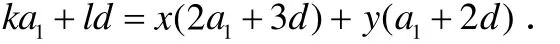
根据上面的分析，例1中的a4=-(2a1+3d)+3(a1+2d)不仅合情合理，而且把2a1+3d和a1+2d 看成基底后，a1和d的制约关系也很完整地保存下来，没有任何的损失和变化，得出正确答案也就不足为奇了．基底概念和平面向量基本定理一经写出，任何语言都显得多余，学生在会心的微笑中豁然开朗，教师顺势给出了下面的练习．

4 案例教学的功效

由于中国目前评价学生数学能力和水平的主要方式是考试，解题又是考试的唯一形式，因此，和解题教学相比，概念在教学中依然扮演着敲门砖的角色，还难以摆脱功利的色彩，学习概念的落脚点只是为了知道某个定义，在例题上有更多的选择，之后教师的重心依然回到解题教学上，解题的诱惑会使师生直奔解题方法，然后通过大量训练积累经验，提高能力．概念对于学生的作用只是表层的显性含义，反映在解题中，就是把已知条件涉及到的概念进行最直接的转化，至于题目的解决要靠教师补充的课外知识、总结的解题规律来完成，以至于很多学生在学完全部高中数学课程后，对很多重要概念不能准确表述，甚至是毫无记忆．引入概念时教师煞费苦心培育出的学生对概念的情感，在随后的题海中荡然无存．这不仅使学生对数学概念本质难以真正理解，也使解题教学的成本大大增加．

从教学案例看出，一方面，概念二次教学能淋漓尽致地暴露思维过程，清晰展现数学方法的来龙去脉，使解题活动成为学生在认知最近发展区内的创造性活动，使解题过程成为学生知识能力的自我生长过程．另一方面，概念的二次教学能充分体现数学概念的价值，使概念的作用显性化，并具有下面的作用．

4.1 发现解题方法的源泉

关注普遍的必然性，是人类基本的思维倾向[7]．反映在解题中，主要表现在学生对解题思路和解题方法的挑剔，“为什么这样做？”“我这样做行不行？”是很多学生看过解法后产生的困惑．对教师而言，解题思路分析是以不变应万变的教法，教师总是试图通过思路分析，来说明某种解题思路的必然性，进而让学生认可这种解法．但是多数的思路分析是建立在知道题目解法的前提下，是在为已知的解法寻找合适的理由，有些题目教师教过几遍了，其解法是经过多次反思的产物，是不断改进之后近乎完美的方法，每一步看起来都很自然，但对第一次接触题目的学生来说却知其然不知其所以然．另外，教师总是无意识地用自己的认知水平来衡量学生，造成解题方法的呈现方式和时机脱离学生的实际，这是学生听得懂却学不会、不会用的原因之一．当人们意识到解题教学应当探索解法得来的过程，让方法的出现自然流畅的时候，又一个问题摆在教师的面前：怎样才能做到这一点？提示2的解法无论如何解释都难以自圆其说，而基底的思想却可让学生茅塞顿开，这让教师有理由把目光聚焦在概念的二次教学上．

教育心理学认为，兴趣是一个人倾向于认识、研究获得某种知识的心理特征，是推动人求知的一种内在力量．兴趣对于学习的重要性不言而喻，用各种手段激起学生的学习兴趣并不困难，难在兴趣的持久和发展．显而易见的刺激只是兴趣的诱因，真正能使学生兴趣得以保持的是兴趣的源泉．知识的力量是产生兴趣的源泉之一，关键是要让学生感受到这种力量．从概念中寻找方法，让概念中的方法在解题中有所作为，这样，数学方法就有了源泉，就不是无根之水无本之木，它会让学生认识到数学概念与数学解题之间的关系，感到数学是平易近人的，是讲理的、简单的，数学方法就在身边，并在方法的运用中享受思维的乐趣．概念在解题中也就不只是标签的作用，不再只是解题的起点，而是贯穿解题过程的灵魂．

在数学教育教学中，主要强调的是知识的发展价值，即知识对于学生的身心素质的形成与发展所具有的促进作用．对于学生的学习和发展而言，并不是所有的知识都是有效的，即使是那些科学、正确的知识，如不能够使学生的身心素质有所增进，那也是无效的知识[8]．基于此，即使学生机械、被动地学会了一种解题方法，然后通过模仿、练习能按图索骥去应用，也没有太大的价值，因为学生的数学思维并没有真正意义上的发展．而有了源泉的方法不仅有较高的实用价值，有利于促进学生思维的迁移，同时对学生的数学观也会产生积极影响，对提升学生认识数学的层次和品位有助推作用．就提示2而言，教师曾对两种教学方法的效果进行比较，一种是直接给出方法，要学生记住，一种是文中的方法．从结果看，学生解类似题目的成功率没有太大差异，在做随后的练习题时也没有差别，前者还有节省教学时间的优势．但随着类似的对比持续进行，区别会逐渐显现出来，尽管考试成绩仍难分伯仲，但前者容易使学生产生消极的数学学习观，认为一种方法只要会用，能得到正确答案，考试能得分，没必要知其究竟，从而失去了进一步探索的欲望，久而久之，潜在的数学天赋会逐渐泯灭，也就难以在数学学习中得到快乐．而后者则在使学生保持浓厚的学习热情，促进数学思维的发展上有持续的作用．

4.2 感受数学文化的价值

教育部2003年颁布的《普通高中数学课程标准》（实验）中把体现数学的文化价值作为课程的基本理念之一，数学文化随之逐渐走进课堂，然而教学中如何体现数学的文化价值，对教师来说还缺乏足够的实践经验支持，对如何把理念转化成教学行为还感到茫然．课程标准中指出数学课程应适当反映数学的美学价值[9]，这是教师认为容易实现的一个理念，于是简洁美、对称美、奇异美在课堂中时有出现．然而，数学的美不仅只是形式上的美，也不仅是看得见、听得到的感官的愉悦，数学的美更体现在数学内容中蕴含的令人神往的无穷魅力，数学的美不一定能够言表，但当你触摸它的时候会引起你的共鸣，触动你的心灵．数学的美“是蕴含于数学知识之中，是从数学内容反映出来的”[10]．“数学逻辑推理中蕴含着美的因素，数学的内在美是一种高尚的理性美”[11]．提示2的解法正是因为平面向量基本定理在内容上体现的协调、平衡之美，才有结果的科学合理．当学生细细品味解法的内涵时，会感受到这种内在的力量，认识到数学方法不仅仅是解题的工具，也是人类智慧的结晶，能给人的思维以启迪．

例2的解决过程也是一个求真的过程，从最初看似合理的方法竟然存在漏洞，到正确方法的出现以及对正确解法的追问，都体现出数学理性的探索精神，而最后基底思想为解法找到归宿，则彰显了概念的生命力．这种问题驱动、层层递进的探索历程带给学生的体验，是单纯介绍解题方法无法比拟的．更重要的是，在这一过程中，学生不是旁观者，而是身心投入的参与者．

数学文化不可能脱离数学内容孤立存在，也不可能只以形式化、表面化的形态出现，它根深于数学思想方法中，它和数学知识是浑然天成，不可分割的．教师要善于发现，然后引导学生在数学文化的氛围中开展数学思维活动，使解题真正成为学生的一种精神需要和追求，成为感受数学的最好载体．在解题中丰富他们的数学情感，在充满着创造力和想象力的文化背景下掌握解题方法，逐渐学会“用数学的思考方式解决问题、认识世界”[9]．

5 教学建议

开展概念二次教学的关键是要有相关的素材，这就需要教师对数学概念、数学思想方法进行重新的思考，需要教师对教学内容进行由此及彼，由表及里的再创造，需要教师不仅具有概念二次教学的意识，更要有把这种意识物化为教学行为的方法．

5.1 各知识之间的联系了然于心是概念二次教学的起点

进行概念二次教学，教师首先要“清晰把握基础教育阶段的数学知识体系，洞悉不同学段教学内容的内在联系”[12～13]．数学各部分知识之间的联系不仅是简单的先后承接，也不单是形式上相互的转化，还包括某个内容中发散出来的思想方法和在其它知识中的应用．具体地讲，例1中通过换元把数列问题转化为线性规划问题，这是形式上的转化，因为不换元同样是线性规划问题，换元并没起决定性的作用；基底的概念和平面向量基本定理是对平面向量而言的，但它在数列问题中能够使用，这是思想方法的应用，这当中虽然也有形式的转化，但这是基于思想的转化，是质的飞跃．把握这种联系是教师的内功，是概念二次教学的必要条件．

教学方法通过教师赋予该方法的内容来发挥作用，缺乏内容的方法是苍白无力的．教师可以通过深入研究教材，多角度全方位审视教学内容，来储备概念二次教学的资本，随着教师对教材独到理解的逐渐增多，就可以随心所欲地驾驭教材和教学内容，设计出内涵丰富充满活力的概念二次教学．

5.2 挖掘概念蕴含的数学思想方法是概念二次教学的途径

尽管挖掘概念中的数学思想方法早已是人们的共识，但由于教师获取解题方法的途径很多，“拿来主义”便是一种常见的方式，用这种方式获取的解题方法多数情况下只是一种结果，教学中教师关注的往往是解法的应用，解法的“起源”常被略去，因此客观存在的解法与概念的关系也就难以被发现，即使从概念中得到了一些数学思想方法，大多也是一种形式化的解读，在解题中少有作为．

概念中的数学思想方法不是从概念表面得来的，它存在于概念的“深处”，需要教师智慧的探索才能发掘，需要教师深入地思考和再加工才能在教学中应用．撇开概念的外延和内涵，提出由概念衍生出的问题，再试着解决这些问题，是深入一步的方法；观察概念形式上的特征，与其它知识作横向的联系，再概括出共性，是再加工的途径．反过来，对常用的解题方法可以采取逆向思考的办法，考察其可能在哪些概念中出现．这个“出现”当然也不是直接能看到的，需要教师反复探索、尝试，可以对用某种解题方法解决的问题一般化或特殊化，这样方法和概念的联系会清晰起来；还可以对解题方法中涉及到的数学式子进行各种变形，变形后可能就会发现概念的踪迹．精彩的教学设计更多来自于从学生质疑中获取的灵感，如果学生对一种解题方法感到费解，教师可以沿着学生的疑问进行思考，从概念中为质疑寻找简单普通的答案．例1解法2中的基底思想，就是“您是怎么想到的？”的产物．

5.3 宽阔的例题教学视野是概念二次教学不断创新发展的基础

学习数学是感知、体验、感悟、生长的过程，这需要学生有足够的实践机会来获取数学活动的经验，从这个意义上说，平时润物细无声的渗透，远比强化训练更有效果，所以教师要有战略眼光，要从学生高中数学学习的整个历程谋划概念教学，要注意现实利益和长远发展相结合的原则，要经得起忍耐和等待，这样概念才能真正发挥其应有的作用，概念的二次教学也才能持续不断地深入发展．例如，有些概念中蕴含的数学思想方法并非某个单元的教学重点，课上加以拓展对概念二次教学大有裨益，但可能会冲淡主题，甚至不合时宜，对新知识的学习产生冲击．这种情况下，可以设置起点低，有递进关系的问题串，分解在几节课上要学生探讨，这样既为二次教学做了必要的准备，也减少了“弦外之音”的投入时间，不至于喧宾夺主．有些解题方法在学习概念之前学生已经掌握，那么在概念学习后，可以让方法再现，以达到“蓦然回首，那人却在灯火阑珊处”的效果，催化学生对方法的深层理解．

5.4 教师创造性的教学设计是概念二次教学的成败关键

数学教师是学生数学学习的榜样，仅从解题教学的角度看，体现在两个方面：一是教师是学生学习解题最直接的模仿对象．学生的模仿包括教师探求解题途径的思维方式，教师对解题方法的选择和偏好等；二是教师对解题的理解、对数学的追求潜移默化地影响着学生对数学的情感和认识．从这个意义上说，数学教师本身就是学生数学学习的资源．概念二次教学能否取得成效，关键要看学习资源为学生提供的学习价值．一般来说，教学设计中融入的教师智慧越多，学生的学习资源就越丰富，对学生身心和智力的发展也就越有益．和一般意义上的解题教学相比，概念二次教学对教师的要求更高，因为目前这方面可供借鉴的成果不多，每一节课都需要教师调动自己的才智进行创造性的教学设计．

在进行概念二次教学的设计时，教师可针对学生可能出现的问题，对储备的素材进行筛选、充实、重组，整合相关知识间的内在联系，找到数学思想方法呈现的最佳时机和最佳方式，用问题触发学生思维，通过反思完善学生的认知结构．文中的案例，如果没有变式的例2，例1中学生的错误就不够彻底，就不会引起对解法的反思，对正确解法的渴望也就不那么强烈；两种正确的解法出现的形式虽然相同，但学生的感触是不一样的，线性规划的方法只要点拨到位学生就能接受，而第二种方法就显得有些突然，而这恰恰为基底的登场做了铺垫；富有深意的练习2则是点睛之笔．

6 结 语

在高中数学例题教学中，面对一道复杂的数学问题，如何展开思路，如何寻找不同的解题方法，如何总结规律，已经有很多颇有见地的成果，但对数学方法产生背景的研究还稍显不足，对学生思维习惯和认知水平没能充分尊重，解题思路的分析过于一厢情愿．对学生来说，面对精妙的解题方法，在欣赏赞叹的同时，又觉得难以亲近、遥不可及；题做了很多，解题经验积累了不少，解题方法上也非常富有，但缺乏驾驭数学方法的方法，亦即没有解题灵魂．从概念出发，用最基本的知识，最简单的方法，最普通的常识，逐步呈现探究的过程，诠释思路的缘由，揭示思维的规律，是使学生热爱数学、向往数学、享受数学的有效途径之一．

[1] 钟启泉，崔允漷，张华．《基础教育课程改革纲要（试行）》解读[M]．上海：华东师范大学出版社，2001．

[2] 钟启泉，崔允漷，吴刚平．普通高中新课程方案导读[M]．上海：华东师范大学出版社，2003．

[3] 李秉德，李定仁．教学论[M]．北京：人民教育出版社，1991．

[4] 王道俊，王汉谰．教与学[M]．北京：人民教育出版社，1989．

[5] 陈玉琨，代蕊华．课程与课堂教学[M]．上海：华东师范大学出版社，2002．

[6] 阮晓明，王琴．高中数学十大难点概念的调查研究[J]．数学教育学报，2012，21（5）：29-33．

[7] 袁缘，李辉来．数学的逻辑思维在人类思想逻辑化进程中的作用[J]．数学教育学报，2012，21（6）：23-26．

[8] 王新民，王富英．高效数学教学构成要素的分析[J]．数学教育学报，2012，21（3）：20-24．

[9] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003．

[10] 戴风明．数学文化在数学教学中的缺失与对策[J]．数学教育学报，2011，20（6）：74-77．

[11] 伏春玲，冯秀芝，董建德．数学文化在中学数学教学中的渗透[J]．数学教育学报，2011，20（6）：89-92．

[12] 王光明，宋金锦，佘文娟，等．建立中学数学英才教育的数学课程系统——2014年中学英才教育数学课程研讨会议综述[J]．课程·教材·教法，2014，（5）：122-125．

[13] 王光明．高效数学教学行为的归因[J]．数学教育学报，2010，19（5）：75-77．

Practice and Thinking about Mathematics Concept Further-Teaching——In a Case of a Teaching Example

LIANG Dong1, ZHU Hong-ling2
(1. Yangcun NO.1 Middle School, Tianjin 301700, China; 2. College of Teacher Education, Tianjin Normal University, Tianjin 300387, China)

Mathematics concept further-teaching is a part of example teaching, which can make students find the source of the solutions to problems and display the cultural value of mathematics at the same time. Familiarity with the interrelation within knowledge is the origin of mathematics concept further-teaching; digging the methods of mathematical thoughts in the concept is the pathway of carrying out the mathematics concept further-teaching. A broaden teaching horizon is the base for the innovation and development of mathematics concept further-teaching and creative teaching design is the key to it.

mathematics concept further-teaching; mathematics thinking method; the culture of mathematics; mathematical thinking

G420

：A

：1004–9894（2015）02–0083–05

[责任编校：周学智]

2014–11–12

天津市教育科学“十二五”规划课题——教育统计与测评技术在高中教学管理中的应用研究（BEYP5007）

梁栋（1962—），男，天津武清人，中学特级教师，主要从事中学数学课堂教学研究．朱鸿玲为本文通讯作者．