小学数学教科书中的概念研究
杜岩岩
(首都师范大学初等教育学院,北京100048)
小学数学教科书中的概念研究
杜岩岩
(首都师范大学初等教育学院,北京100048)
概念是思维的基本形式之一,也是判断和推理的基础。对小学数学教科书中概念的有效理解能够促进学生思维能力的发展。运用内容分析法梳理小学教科书中的重要概念,总结出概念的结构、分类、定义类型、呈现方式等方面的现状。从逻辑学、心理学的视角分析小学教科书中概念教学中存在的问题,依据相关理论,并运用案例分析法对不同方面的问题提出针对性的策略,从而促进数学概念的有效学习,这对于学生的思维发展大有裨益。
小学;数学;教科书;概念
数学概念是一类数学对象的本质属性的反映[1],同时它也是数学基础知识的基石。《义务教育数学课程标准》(2011年版)[2](以下简称《数学课程标准》)的前言部分强调:“推理能力的发展应贯穿于整个数学学习过程中。”推理能力发展的基础是概念,所以,概念的学习对于学生来说至关重要。然而在小学实际教学中,学生对于数学概念的理解和掌握存在许多困难,而教科书作为学生学习数学概念的主要资源,是如何呈现概念的呢?它对概念的学习有怎样的影响呢?
一、概念在教科书中的呈现
数学是研究数量关系和空间形式的科学,因此数学概念是数量关系和空间形式的本质属性的反映。对于数学来说,只有掌握了数学基础知识,实现知识之间联系,才能在活动中提高基本技能,发展基本思想。下面以北京师范大学出版社出版的《新世纪(版)义务教育课程标准数学实验教科书·数学》(1~12册)(以下简称北师版教科书)为对象,从概念的结构、概念的分类、概念的定义类型、概念的呈现方式方面来具体分析。
1.概念的结构
概念的结构是指概念由哪些部分组成,一般来说,概念是由名称、属性、定义和例证组成的(如表1所示)。概念的名称一般由词汇构成,例如三角形、四边形等。概念的形成并不一定必须用一个特定的词说出来,例如婴儿无法使用语言表达概念,但能够从许多人中辨认出妈妈,说明“妈妈”的概念已经形成。实际教学中有的学生说不出“周长”的概念是什么,但他能够清晰地指出物体中的边界的长,这表明学生对于“周长”的概念已经形成。概念的属性指的是概念的关键特征,例如物体的颜色、气味、材料、大小、形状、位置等。数学概念只研究物体的大小、形状、位置、数量关系等属性。逻辑学中,概念的定义就是以简短的形式揭示概念、命题的内涵或外延,使人们明确它们的意义及其使用范围的逻辑方法。[3]概念的例证大致分为两种:一种是正例(positive instances),即与概念要求相符,例如,4是正数的正例,等腰三角形是三角形的正例;另一种是反例(negative instances),即与概念要求不符合或违背要求的,例如,-2是正数的反例,平行四边形是三角形的反例。

表1 概念结构分析表
2.概念的分类
根据不同的分类标准可以将概念分为不同的类型,例如,奥苏贝尔根据是否经过观察正反例子揭示概念的特征把概念分为初级概念和二级概念(如表2所示)。[4]例如,三角形是初级概念,等腰三角形是二级概念。

表2 概念分类举例表
《数学课程标准》将义务教育阶段数学课程内容划分为四大部分:数与代数、图形与几何、统计与概率、综合与实践。其中的前三部分包括许多数学基本概念,综合与实践是对概念的应用。依据前三部分内容的分类,对北京师范大学出版社出版的《义务教育课程标准实验教科书·数学》1~12册中的数学概念进行梳理,结果如表3所示。

表3 概念分类表
3.概念的定义类型
对概念的不同定义类型进行分析,不仅能够促进学习者对概念的更好理解,更重要的是能够让学习者领会概念定义的不同种类及含义。北师版教科书中的有些概念没有明确定义,而是采用直接给出的形式,这在低年级教科书中比较普遍。通过梳理教科书中明确定义的概念并从逻辑学角度对概念的定义类型进行分析,可以将北师版教科书中数学概念的定义概括为:发生定义、关系定义、语境定义、列举定义、实指定义、描述性定义。
发生定义是指从被定义的词项所指称的事物的发生、来源方面揭示种差定义的形式。例如最小公倍数,通过从公倍数中选择最小的倍数来定义;关系定义是指以事物之间的特殊关系作为种差的定义,例如,倒数是以两个数的乘积为1的特殊关系来定义的;语境定义是指将定义项放在一定的语言环境之中,然后用一个意义相同但被定义项在其中不出现的语句来给被定义项下定义,这种定义强调具体的上下文语境;列举定义属于一个概念的外延的对象数目很大,或者种类很多,无法穷尽地列举,于是就举出一些例证,以帮助人们获得关于该概念所指称对象的一些了解;实指定义通过用手指指着某个对象,从而教会儿童去认识事物和使用语言,这种定义能够通过具体事物来帮助学生理解概念;描述性定义是指对被定义语词既有用法的报道或描述(如表4所示)。[4]
我不知道,在这个世界上,关于爱,一共有多少种表达方式,但我知道,最朴素最深情的一种,就是——养一只羊,等你回家。

表4 概念的定义类型
4.概念的呈现方式
这里所讲的概念的呈现方式是指教科书中以什么材料来呈现概念:有些概念只用文字语言来呈现,例如长方体的表面积;有些概念的呈现可能既有文字又包括图形,在不同的概念呈现中二者的比重不同。通过总结,可以把呈现方式大致分为三种:图形主导文字辅助型、图文并茂型和文字描述型。
图形主导文字辅助的这种呈现方式主要分布在北师版低年级教科书中,这个阶段的儿童具有皮亚杰关于儿童的发展理论中的具体运算阶段的特点,抽象思维能力薄弱,对于文字的认识、理解、使用等方面的能力尚处于较低水平,不能在头脑中很好地实现文字与其所代表的具体事物的转化。采用直观图形为主,文字辅助的方式(如图1所示)[5]有利于学生从直观的图形获得对于概念的有效理解。这种呈现方式的概念有:长方体、正方体、球、圆柱、圆锥、圆、线段、射线、直线、角、平角、周角等。
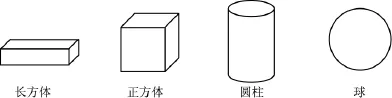
图1 认识物体
图文并茂呈现方式(如图2)[6]指的是图形与文字在呈现概念时不分主次,处于同等的地位,这种呈现方式大多分布在中、高年级的教科书中。随着学生年龄的增长,对于文字的理解力也逐渐增强,从图形和文字不同方面对概念进行理解,有利于对概念的不同角度的理解,实现文字与图形之间的联系,这有利于发展学生的图形语言和文字语言。这种呈现方式的概念有:锐角、直角、钝角、等腰三角形、等边三角形、梯形、平行四边形、垂直、周长、面积等。
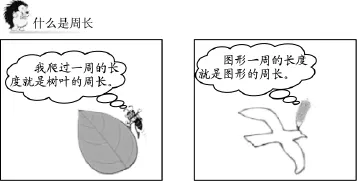
图2 周长的定义
文字描述的呈现方式[7]是指仅采用文字语言来描述概念,没有搭配对应的图形。这种概念呈现方式一般分布在高年级的教科书中,这个阶段的学生的思维水平和使用文字的能力进一步提升,这为理解文字奠定了基础。文字描述的概念呈现方式能够帮助学生实现文字与概念对应的原型之间的转换,从而发展学生的抽象思维能力。这种呈现方式的概念有:表面积、体积、容积、小数、分数、速度、正数、负数、循环小数、自然数、整数、倍数、因数、最小公倍数、最大公因数、偶数、奇数、质数、合数、倒数、中位数、众数、约分、通分、方程、比、正比例、反比例、比例尺等。
二、对概念呈现现状的分析及建议
根据小学生的年龄特征和认知水平,教科书中的概念有些仅给出了概念的名称,有的只是描述了概念外延的一部分,有的则是采取了定义的方式,这些不同的形式,有利于学生从不同角度去理解概念;同时,北师版教科书概念的呈现情况中也存在一些问题,对问题进行分析从而更好地促进概念的学习。
1.概念的结构方面
对北师版教科书中呈现的概念的结构进行分析后发现,书中对于概念的反例的呈现数量明显少于正例,甚至很多概念没有呈现反例。例如,在方程的概念结构中,只给出了像x+5=10,4y=380这样的正例,对于不是方程的反例却没有给出。又如,在最简分数的概念结构中仅呈现了像这样的正例,同样也没有给出不是最简分数的反例。这说明北师版教科书对数学概念结构的呈现并不全是完整的,存在缺少反例的现象,而反例对于概念的学习至关重要,正如Markle所说,反例在概念的学习中应该处于主导地位。
概念学习本质是对概念属性的辨认,而例子则是概念属性的具体化和形象化,对概念的学习有着重要的辅助作用。[8]每个人回忆自己的学习过程就会理解例子的重要性,正如有关研究表明,核心概念教学时,如果没有后继的样例学习和练习,儿童数学问题解决水平较低。[9]正例让学习者明白概念是什么,反例让学习者晓得概念不是什么,这种对比的方法,可以让学生明确概念的关键特征,从而加深对概念的理解。在学校教育中,教科书对教学有重要的影响。然而,正如McKinney等人所指出一样,大部分的教科书中都没有呈现概念的反例。[10]因此,适当增加教科书中概念的反例数量,以符合学生思维特征的方式呈现它们,并且合理组织正反例,让学生在正例、反例的对比中去重新认识、理解概念。
2.概念的分类方面
对概念进行分类,有利于学生弄清楚概念的含义及概念之间的关系。教科书中按数与代数、图形与几何、统计与概率分为三部分内容,在每个单元里介绍其中一部分内容中的概念,这样有利于学生系统地掌握概念,但是同时不利于学生沟通其他部分内容里的知识的联系。因为学生在学习概念时,头脑里的知识不是孤立的,而是相互联系的。概念教学不能只满足于告诉学生“是什么”或“什么是”,还应让学生了解概念的背景和引入它的理由,知道它在建立、发展理论或解决问题中的作用。[11]所以教科书不仅要让学生知道按照数学课程内容分类的概念是什么,还要让学生明白为什么这样分类。例如,面积的概念属于图形与几何的内容,但学生头脑中有时把面积看成数与代数的内容,因为在用数格子法求面积时学生仅仅关心面积的大小是多少,而忽略了图形的形状。由此可见,教科书应该鼓励学生按照不同的标准给概念分类,这有利于从不同角度看概念,从而沟通概念之间的联系。
3.概念的定义方面
定义在概念学习中是十分有用的,通过定义学生更好地辨别概念相关属性,从而减少不必要的麻烦。从教科书中的概念定义可以看出,几乎所有概念的定义方式只有一种,这说明概念的定义方式比较单一,不利于学生从多角度理解概念。而且,概念的定义在教科书中出现的次数较少,有的概念在小学阶段只出现一次。
针对教科书中定义方式单一,建议采用两种或多种定义方式结合的方法定义概念。例如,可以先给出分数概念的发生定义,再利用列举定义给出该概念的一些外延。另外,定义方式要与年龄特点相符合,低年级阶段要多采用实指定义,再逐步发展到用文字叙述的其他定义,例如低年级定义正方形,可以指着图形说像这样的图形叫正方形,高年级可以定义它为四边都相等的长方形叫正方形。同时,在概念学习的不同阶段,用不同形式的语言去定义概念,让不同形式的概念定义多次出现,这使得学生能够循序渐进地理解概念。
4.概念的呈现方面
整体来说,北师版教科书中概念的呈现运用了大量生动活泼的情景、直观形象的图形、简明易懂的文字。但梳理后从中也发现了一些问题,例如在图形主导的呈现中多数图形都是从现实物体抽象而来,没有把图形与现实物体联系起来。文字描述的概念对应的图形有些不是概念的最佳实例,例如,树叶和简易鸽子的图形不是学生日后学习周长中常用例子,且鸽子的图形相对复杂,有些学生借助它理解周长的概念可能会遇到许多障碍。因此,第一次出现某种图形时,图形要与实例一起呈现,同时实例最好是符合概念的最佳实例。文字的力量是巨大的,但这种力量必须在文字被理解的情况下发生。而教科书中存在一些呈现概念的文字较难理解的现象,这不利于学生对新概念的理解。因此,教科书中不能用学生难懂的文字去定义概念,尽量在定义中避免学生不明白的语言。例如体积定义中的“空间”对于学生来说很难理解,而美国加州版教材中关于体积定义“物体所能容纳的单位立方体的数目”[12]给了我们定义体积的另一种角度。
三、结语
学校里的学习通常被认为包括概念学习、技能学习和问题解决三部分。[13]例如斯坦福数学学业成就测验的内容由概念、计算和应用组成。由此看出,概念的学习已经成为各个学科课程内容中不可分割的一部分。教科书作为概念呈现的主要载体,其中概念的呈现方式对于概念的学习有重要影响。数学课程内容中的概念是帮助学生和教师理解数学的基础,而一本具有合理组织概念、准确定义概念、清晰呈现概念的教科书无疑对教与学都有很大帮助。因此加强概念教学,可以从教科书开始,通过增加教科书中正反例的对比学习等方式提升教科书的质量,使之成为学生进行概念学习的重要资源、教师进行概念教学的有力工具。
[1]李善良.现代教学观下的数学概念学习与教学理论研究[D].南京:南京师范大学,2002.
[2]教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2011.
[3]陈波.逻辑学十五讲[M].北京:北京大学出版社,2008:79.
[4]陈琦,刘儒德.当代教育心理学[M].北京:北京师范大学出版社,2007:270.
[5]义务教育数学课程标准研制组.义务教育课程标准数学实验教科书:第一册[M].北京:北京师范大学出版社,2005:64.
[6]义务教育数学课程标准研制组.义务教育课程标准数学实验教科书:第五册[M].北京:北京师范大学出版社,2006:44.
[7]义务教育数学课程标准研制组.义务教育课程标准数学实验教科书:第十册[M].北京:北京师范大学出版社,2005:18.
[8]郭建鹏,彭明辉,杨凌燕.正反例在概念教学中的研究与应用[J].教育学报,2007,3(6):21-27.
[9]李运华.核心概念教学思维对儿童数学问题解决的影响[J].重庆师范大学学报:自然科学版,2013,31(2):117.
[10]McKinney C W,Larkins A G,Ford M J,et al.The Effectiveness of Three Methods of Teaching Social Studies Concepts to Fourth-grade Students:An Aptitude-treatment Interaction Study[J].American Educational Research Journal,1983,20:663-670.
[11]邵光华,章建跃.数学概念的分类特征及其教学探讨[J].课程·教材·教法,2009,29(07):49.
[12]Altieri.California Mathematics Grade 3[M].New York:The McGraw-Hill Companies,2007:487.
[13]Richard J Shumway,Arthur L White,Patricia Wilson and Bruce Brombacher.Feature Frequency and Negative Instances in Concept Learning[J].American Educational Research Journal,1983,20(3):451-459.
[责任编辑:陈学涛]
G623.5
A
1002-1477(2015)03-0076-05
10.16165/j.cnki.22-1096/g4.2015.03.018
2014-07-04
杜岩岩(1989-),女,安徽亳州人,硕士研究生。

