引导学生主动参与学习之我见

吴春燕

【摘要】 课堂教学效率的高低主要是以学生参与学习的程度来决定的. 参与是学生心理的需要，是认知发展的需要，也是主动探索知识、培养创新意识的需要. 教学中可以通过设好开讲引参与、加强操作乐参与、因材施教皆参与、引导自学会参与.

【关键词】 参与；开讲；操作；因材施教；自学

《数学课程标准（2011版）》明确指出：“学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者. ”同时《新课标》强调，要把传统的“以学科为中心”转移到“以学生为中心”“一切为了学生的发展”. 现代教育理念与教学实践告诉我们，教学过程应该是教会学生学习的过程. 课堂教学效率的高低主要是以学生参与学习的程度来决定的. 参与是学生心理的需要，是认知发展的需要，也是主动探索知识、培养创新意识的需要.

一、设好开讲引参与

良好的开端是成功的一半. 课始，通过学生感兴趣的故事、游戏、竞赛、模拟情景等吸引学生，使学生带着炽热的追求和疑问参与新知的学习.

每节课的开讲，应根据不同的内容，采用不同的方法，一般的做法是：以疑激欲、以趣激欲、以境激欲. 如：教学“有余数的除法”采用以疑激欲开讲：大森林里，小动物们正在举行数数比赛. 狮子当裁判，小猴、小鹿、小狗、小兔依次围在狮子的身旁. 裁判宣布比赛规则：从小猴开始，小猴、小鹿、小狗、小兔分别数1、2、3、4. 每一个数字都会对应到一只小动物身上. 比赛时，我报出一个数，这个数数到谁，谁必须马上回答“是我”. 比赛正式开始了，只听裁判刚报“19”，小狗马上接口：“是我. ”“25”，小猴又及时地接上“是我”. “34”则是小鹿在喊“是我”. 每一次回答都是那么干脆、敏捷，得到裁判的充分肯定. 它们怎样很快作出判断呢？孩子们迫切想知道答案. 这时教师适时告诉学生：学了今天这节课的知识后，你们就能解决这个问题了. 不到2分钟的开讲，将孩子们的求知欲完全调动起来，参与新知的学习成了孩子们内心的需要.

又如：教学“小数的性质”，采用以趣激欲开讲：出示“3、30、300”三个数，问：“谁能用适当的单位名称并用等号将这三个数连起来？”这个问题，引起了学生的浓厚兴趣，通过认真思考，有的说“3元 = 30角 = 300分”，有的说“3米 = 30分米 = 300厘米”. 课堂气氛异常活跃，此时，我又提出一个问题：“谁能加上同一单位名称将上面三个数用等号连起来？”学生听后，思维更加积极，提出了“3元 = 3.0元 = 3.00元”“3米 = 3.0米 = 3.00米”. 最后，我接着问：“像3，3.0，3.00这样的数大小是否相等呢？为什么？这节课我们一起学习这个问题——小数的性质. ”这简单的三个数，引发了学生浓厚的学习兴趣，激活了学生的思维，促使学生愉快地进入参与探求新知识的学习过程.

再如：教学“相遇问题”采用以境激欲，一上课，为学生创设这样一种环境，出示“相遇、相距、同时、相向”这四个词，师：“同学们，你们能用动作和语言来表演这四个词的意思吗？”一下子，孩子们就活跃起来了. 这种情景的设计，就是让孩子们在实践当中自己去理解概念，展开新课.

二、加强操作乐参与

马芯兰老师说：“儿童的智慧在他的指尖上. ”新的教学理念认为：要让学生动手做科学，而不是用耳听科学. 只有动手操作和积极思考才能出真知. 如教学“三角形的认识”一课，先让学生找出情境图中的三角形并利用课件标出三角形的轮廓后，组织学生动手操作，利用准备好的材料想办法做一个三角形，要求边做边思考：“什么样的图形是三角形？三角形有哪些特点？”交流时有的学生说：我用3根小棒摆了一个三角形；有的学生说：我在钉子板上围了一个三角形；还有的学生说：我沿三角尺的边画了一个三角形……教师逐一展示学生的几种做法，引导学生观察做的三角形思考：“大家做的三角形材料不同、形状各异、大小也不同，有相同的地方吗？什么样的图形是三角形呢？”再用自己的话对三角形的概念进行描述，最后请学生闭眼想一想，在本子上画一个三角形. 通过学生动手操作和教师的问题“大家做的三角形材料不同、形状各异、大小也不同，有相同的地方吗？什么样的图形是三角形呢？”将学生的注意力引向对三角形的本质属性的关注，再通过学生动手画三角形后的辨别与修正活动，很快突破概念理解的难点，实现对三角形意义的建构.

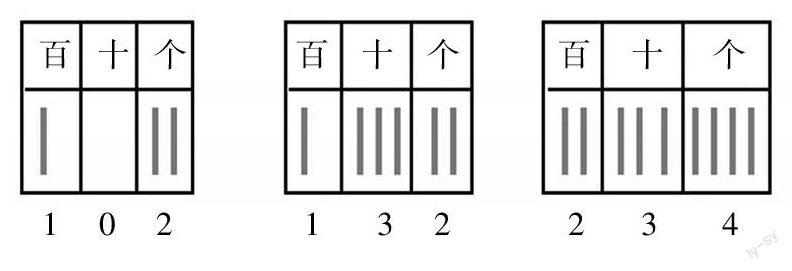
动手操作起到了化静为动、以动促思的效果，符合学生好动的心理特点，有利于激发学生参与的乐趣. 在教学中，凡是能够操作的，教师都应结合具体的内容创造条件让学生动手操作，通过对学具的摆、剪、拼、移进行操作，调动多种器官参与感知. 如教学“能被3整除的数的特征”教法A：通过观察几组数，引导学生得出能被3整除的数的特征. 教法B：让学生动手摆火柴棒，依次用3根、6根、9根，2根、5根、8根……火柴棒摆在数位表上（如下图），一边摆一边讨论：用3根、6根、9根火柴棒摆出的数能不能被3整除？用3根、6根、9根火柴棒能不能摆一个不能被3 整除的数？用2根、5根、8根火柴棒摆出的数能不能被3整除？学生兴致勃勃地动手操作，在操作中，他们发现了规律，正确地概括出能被3整除的数的特征. 教法A显然没有教法B能引起学生的参与乐趣，达不到后者的效果，重要的原因是忽视了让学生动手操作.

三、因材施教皆参与

《数学课程标准（2011版）》指出：“不同的人在数学上得到不同的发展. ”在课堂教学中，学习目标的制定不仅要根据课标、教材的要求，也要充分考虑学生的实际需要. 要做到让全体学生都能自觉主动地参与学习，唯有做到因材施教，实施分层教学. 教师要根据教学目标拟定编题计划，确定检查本节课知识的题型和数量，再配置供好、中、差学生练习的有区分度的题，这类题包括课内的反馈练习、课堂作业及课外的家庭作业，如反馈练习设计有必做题和选做题，要求学困生做必做题，中等生做必做题和较简单的选做题，优等生两种题都要做；对于一题多解的题，要求学困生用一种方法解答，中等生用两种方法解答，优等生则用两种以上，并且要列出最佳解法. 对于超要求的同学，给予大力表扬. 这样教学使各个层次的学生都能参与学习，在原有基础上得到发展，获得成功，培养了他们的自信心.

四、引导自学会参与

邱学华老师说：“引导学生自学，是学生主动参与的重要形式. ”教师应放手让学生自学，授予自学的方法，引导学生围绕这几个方面自学：① 自学的内容是什么？包括几个部分？② 新知的学习与哪些旧知识有关？③ 应该特别注意什么？④ 记下不懂的地方；⑤ 举例说明学到的新知识等. 如：教学“异分母分数加减法”时，先让学生自学，说自学心得. 生①：本节课的重点是要求我们掌握异分母分数加减法的计算方法；生②：学新知要用的旧知识是通分、同分母分数加减法的计算方法；生③：为了学好新知要先复习通分，异分母分数加减法的关键是通分；生④：为什么要先通分？有了这样的自学水平，学生的参与就更有广度和深度了.

总之，教师要动用一切可能的手段，为学生创设各种参与数学学习的条件，让每名学生都有参与和表现自己的机会，使学生真正成为学习的主人.