刍议高中数学解题中的一个重要思想

郭瑞

【摘要】“数无形时不直观，形无数时难入微”道出了数形结合的辩证关系，数形结合简言之就是：见到数量就应想到它的几何意义，见到图形就应想到它的数量关系。在高学数学教学中，数形结合对启发思路，理解题意，分析思考，判断反馈都有着重要的作用。数形结合渗透在中学数学的每个部分，根据数形结合的观点，可以通过对数量关系的讨论来研究图形的性质，也可利用图形的性质来反映变量之间的相互关系，因此数形结合可以使数和形相互启发、相互补充、相互印证。本文将对数形结合思想在高中解题做一探讨。

【关键词】数性结合；数学思想；高中数学

数学是研究现实世界的空间形式和数量关系的科学（恩格斯语）。数学中两大研究对象“数”与 “形”的矛盾统一是数学发展的内在因素，数形结合是贯穿于数学发展历史长河中的一条主线，并且使数学在实践中的应用更加广泛和深入。一方面，借助于图形的性质可以将许多抽象的数学概念和数量关系形象化、简单化，给人以直觉的启示。另一方面，将图形问题转化为代数问题，以获得精确的结论。这种“数”与 “形”的信息转换，相互渗透，不仅可以使一些题目的解决简捷明快，同时还可以大大开拓我们的解题思路，为研究和探求数学问题开辟了一条重要的途径。

因此，数形结合不应仅仅作为一种解题方法，而应作为一种重要的数学思想，它是将知识转化为能力的“桥”。而课堂中多媒体的应用更有利于体现数形结合的数学思想方法，有利于突破教学难点，有利于动态地显示给定的几何关系，为学生创设愉快的课堂教学气氛，激发学生的学习兴趣，使学生喜欢数学，爱学数学。下面结合笔者教学过程中，讨论此思想方法在中学数学解题中的具体应用。

1．利用数形结合解决函数问题

例1求函数 的值域。

解法一（代数法）：则 ，得

而

解不等式得

所以函数的值域为：

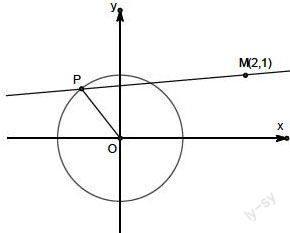
解法二（几何法）： 的形式类似于斜率公式

表示过两点 的直线斜率

由于点 在单位圆 上，（见下图）

显然，

设过 的圆的切线方程为

则有 ，解得

即

所以函数的值域为：

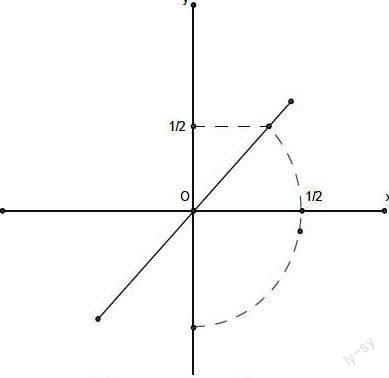
例2求函数 的值域。

解：有函数解析式易知，此函数定义域为

令

由图可知，当 时

=

故所求值域为（- ， ）

函数的图象是函数对应规律的几何表示能直觀的反映函数的性质，是解决问题的有力工具，问题关键是把函数的性质与图像的性质结合起来，亦即形与数的结合。

2．利用数形结合解决解析几何问题。

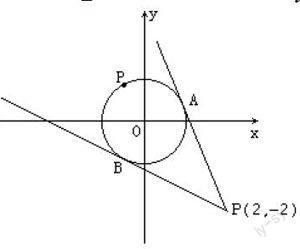
例3求函数 的最大值和最小值。

分析： 的形式相似于斜率 的形式，因此可以把看作是动点 与定点 连线的斜率，所求问题转化为求斜率 的最大值和最小值，由于动点在圆上，因此可以把这个问题转化到图形上来处理。

解：由题意，作出如图，所要求的函数 的最大值与最小值，就转化为求动点 与定点 连线的斜率的最大值与最小值。从图中可以得知，当直线 和圆相切时，分别得到其最大值与最小值，设直线 的斜率为 ，所以，其方方程为 ，即 。当直线 与圆相切时， 即

（上接第160页）

解得 或

所以

例4已知 表示曲线有公共点，求半径 的最值。

解：将方程

化为标准方程

它表示中心在 ，长半轴为2且在x轴上，短半轴为1的椭圆。

方程

表示圆心在 的同心圆系，如图2易知：当 ，两曲线有公共点。

所以  =6

利用数形结合解决解析几何问题时，借助曲线方程使抽象问题形象化，将数量关系直观化是解决问题的关键。

总之，数学研究的对象本身就是现实世界中的数量关系和空间形式，所以数形结合往往使一个问题的两个方面互相映射，互相转化，使抽象思维和形象思维交互作用，从而达到优化解题的目的。数形结合既具有数学学科的鲜明特点，又是数学研究的常用方法.纵观多年来的高考试题，利用数形结合思想解题比比皆是，因此在教学中应引导学生树立数形结合的思想，以形助数巧解代数问题。

参考文献：

[1]李玉琪.中学数学教学与实践研究[M].北京：高等教育出版社，2006.6.

[2]梁法驯.数学解题方法[M].武汉：华中理工大学出版社.1995.3.