初中学生数学易错题成因分析及对策研究
唐小平 雷晓宏
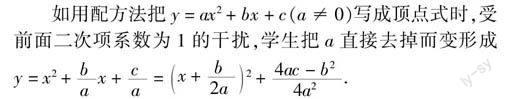
【课题编号】 甘肃省教育科学“十二五”规划2014年度“初中学生数学易错题分析研究”课题(课题批准号:GS[2014]GHB0668)成果.
初中学生数学易错题是指初中学生在认知和解题过程中由于“对概念理解不清”等出现的一些学生容易做错的题.对于学生的易错题,经笔者仔细、深入、全面地调查,得出了学生解题出错除外因(学科多、内容杂)之外,还有内因(学习基础、行为习惯、学习态度),具体如下:
一、受小学数学知识的干扰
如在小学里两数之和大于每个加数.但上初中引入负数后,也可能出现两数之和小于每个加数的现象.
二、进入中学受前后知识的干扰
如用配方法把y = ax2 + bx + c(a ≠ 0)写成顶点式时,受前面二次项系数为1的干扰,学生把a直接去掉而变形成
三、受思维定式(或思维片面性)的影响,考虑问题不全面,出现漏解或增解
1. 如:“数轴上点A到原点的距离是6,则点A表示的数是 .”学生只考虑点A在数轴正半轴的情况或在数轴负半轴的情况.
2. 做“两圆相切的题”,做 “已知等腰三角形一个内角,求另外两个内角或已知等腰三角形两边长,求周长”的题时,学生只考虑一种情况.
3. 忘记勾股定理只适用于直角三角形或受思维定试的影响,误认为c永远是斜边,不知道公式形式应随直角三角形顶点字母的改变而改变.
4. 画函数图像时不考虑自变量的取值范围或不考虑问题的实际意义.
四、对概念理解不清、不透彻,或混淆概念间的内涵
1. 混淆平方根和算术平方根、轴对称和轴对称图形、切线和切线长等概念.
2. 对整式中项的系数和次数、同类项的概念理解不透彻.如在学习同类项概念时误认为2x2y与2x3y2是同类项.
3. 不能正确理解分式概念的内涵.如把圆周率π错看成字母,混淆分式的值为0与分式无意义的区别.
4. 对无理数概念理解错误.如误认为:无理数是无限小数,无理数是带根号的数,无理数是开方开不尽的数,无理数是 “无道理”的数等.
5. 对因式分解的概念理解不清、不透彻而把一个多项式化成几个整式的和的形式或分解不彻底、循环分解,混淆整式乘法和因式分解等.
6. 对数轴概念理解不清、不透彻而导致画数轴时出现以下错误:缺原点、缺正方向、两个正方向、缺单位长度、单位长度不统一、将数字标错(正数标在负半轴上等)、将数轴的形状画成线段或射线.
7. 混淆相反数、倒数、绝对值的概念,误认为有理数a的倒数是,对正、负数表示相反意义的量的认识模糊.例如:将气温-6℃的意思理解为零下-6℃.
8. 错误利用概率公式或树状图画得不完整.
五、粗 心
1. 解分式方程时给不含分母的项漏乘最简公分母以及忘记检验.
2. 解方程时由于变形错误而失根.
3. 将运算符号、性质符号漏掉或混淆.
4. 将“三线合一”说成等腰三角形的角平分线、中线和高互相重合.
5. 判断两直线的位置关系时忘记 “在同一平面内”,用圆周角定理解题时忘记 “在同圆或等圆中” 等 .
六、对有关性质、法则理解不对或滥(误)用运算法则(运算律)
1. 去括号时忽略括号外面的负号,括号里面的各项部分变号或不变号.
2. 混淆或滥(误)用30°,45°,60°角的三角函数值.
3. 滥(误)用整式的乘法公式,极差、方差、标准差公式,有理数加法(减法、除法、乘方)和合并同类项法则等.
4. 滥(误)用不等式性质导致在不等号方向是否改变的问题上出错.
七、混淆性质与判定、定理与逆定理
1. 混淆平行线、全等三角形、角的平分线、等腰三角形、特殊的平行四边形、相似形等的性质与判定.
2. 混淆勾股定理与其逆定理.
八、重视默认条件而忽视隐含条件
1. 忽视算术平方根、绝对值、完全平方式的非负性,忽视一元二次方程有实数根的充要条件是其判别式非负.
2. 求出的方程的根不符合实际问题或将实际问题转化为数学问题时只重视默认条件而忽视隐含条件.如实际问题中一次函数的图像不再是直线.
九、缺乏空间想象力
圆锥中蚂蚁爬行最短距离问题及解答三视图与投影问题时缺乏想象力.
十、违背客观规律,由心自造,想当然凭直觉解题
1. 作函数图像时,忽略自变量取值范围,不按自变量从小到大的顺序依次连线,没有用光滑的曲线连接各点而出现尖点或拐点,忘记曲线的发展趋势.
2. 凭直觉来感知概率或对概率认识错误,错误判断必然事件和随机事件,在普查与抽查中胡乱选择调查方式.
3. 不能正确选择平均数、众数、中位数中的哪一个量来反映数据的集中程度;求中位数时没有对相应数据先排序,再根据数据个数的奇偶性计算.
4. 由心自造三角形全等条件(如用不成立的边边角证题),用待证的结论做论据.

