寻根究底 变“被动”为“主动”
黄莉
方程作为一种重要的数学思想方法,它对丰富学生解决问题的策略,提高解决问题的能力,发展数学素养有着非常重要的意义. 通过列方程解决实际问题的学习能使学生学会运用方程思想去思考、解决问题,使学生获得进一步发展的数学知识,获得基本的数学思想方法和必要的应用技能,发展学生的数学思维能力. 但在具体的教学实践中,我们看到大部分的学生认为学习方程难,解方程的过程复杂,用方程解决问题则更复杂,因而很多学生不喜欢,更不善于用方程的数学思想方法解决问题.
一、学习方程 “被动”现状调查
2014年3月17日,笔者在进行六年级上册第二单元《百分数的应用》教学之前,为了清楚地了解笔者所任教的两个班级学生列方程解决问题的能力,特作了简单的对比检测,具体内容如下:
① 世界上体重最轻的鸟是蜂鸟. 一只麻雀的体重是81克,比蜂鸟的50倍还多1克. 一只蜂鸟重多少千克?
② 姐姐和弟弟一共有180张邮票,姐姐邮票的张数是弟弟的3倍,姐姐和弟弟各有多少张邮票?
③ 一件衣服打8折出售后是240元,这件衣服的原价是多少元?
④ 某商场9月份的营业额是480万元,比8月份增加了,商场8月份的营业额是多少万元?
⑤ 学校为六年级办公室购买了1张新桌子,5把椅子,共计230元,桌子的单价是80元,你能算出每把椅子的单价吗?
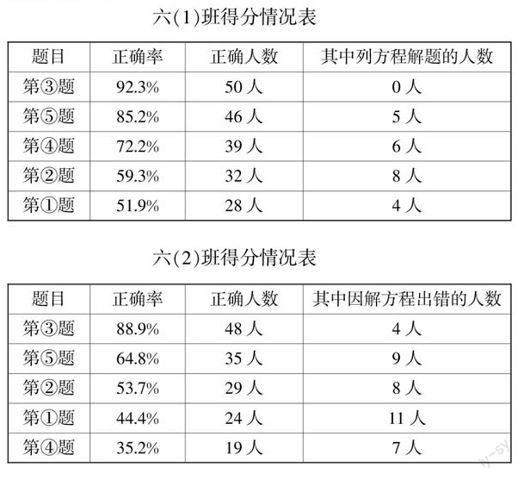
以上5个问题,要求六(1)班的孩子用自己认为合适的方法解决,而要求六(2)班的孩子用列方程解决(孩子们在拿到题目后怨声一片,一再追问:“能不能不用方程解?”). 检测后整理如下:
六(1)班得分情况表
六(2)班得分情况表
以上检测的样本虽小,但却能从对比的数据中反映出学生在用方程解决问题的过程中存在的许多问题. 我们明显地看到孩子们列方程解决问题的意识不够,在没有明确要求用列方程解决问题的情况下,六(1)班的孩子只有为数几人想到列方程,而六(2)班的孩子在被强制用列方程解决时,正确率明显低于六(1)班,而且很多孩子在解方程的过程中又错误百出. 孩子们完全是在“被动”地列方程解决问题. 那么如何化“被动”为“主动”,提高学生列方程解决问题的能力,这是值得我们一线教师思考与研究的新课题. 笔者结合平时的方程教学,通过对学生学习方程“被动”现状的分析,提出提高列方程解决问题的几点策略.
二、学习方程“被动”现状分析
(一)受“老方法”的计算影响,学生排斥用等式性质解方程
新课标实验教材是利用等式的基本性质教学解方程,而大部分的学生认为用等式基本性质解方程,书写步骤多,解题较复杂,容易出现错误等. 相反,对加、减、乘、除各部分之间的关系非常熟悉,利用其相互间的关系解方程不仅显得容易,而且书写的步骤也简单清晰. 因此,多数学生排斥用等式的方法解方程.
另外,学生们认为等式的性质解方程并不是“万能”的. 当碰到像a - x = b,a ÷ x = b这样的方程时,学生们无法用等式的性质来解方程,如同在外面兜了一圈的孩子,不得不又走回了老路——用“减数=被减数-差、除数=被除数÷商”的“老方法”来解决. 孩子们在新方法与老方法之间不停地徘徊,导致他们解方程的思路不清,方法混乱,解方程能力不足. (二)受“逆运算”的迁移,学生列方程解题意识薄弱
现行的教材从低年级开始,就十分关注对逆向思维问题的教学,如一年级下册的“原来有多少”,二年级的“比什么多多少或少多少”“是什么的几倍”等逆向问题,为了让学生理解这些逆向思维问题的基本思路及数量关系,教师可谓煞费苦心,使之逐步成为学生解决问题的一种基本思想方法. 而正因为学生对代数的逆向思维问题学得比较扎实,故在解决问题时,学生想到用算术方法解决问题.
(三)受“旧传统”的教学影响,教师忽视方程思想的渗透
史宁中教授曾指出:“方程思想的核心内容有两个:一个是建模,一个是化归. 建模是用自然语言将生活中的具体事物描述出来,再将自然语言进行数学表达,然后用数学符号建立方程,解决具体问题;而化归思想是用替代的方法,将问题简化为已熟知的内容,用熟悉的算法来解决当前的问题. ”可在实际教学中,有些教师为了让学生掌握答题技巧,考试中获得高分,只根据传统教学经验,注重对学生进行列方程式和解方程的训练,却忽略了对学生方程思想的渗透.
三、学习方程化“被动”为“主动”的对策
笔者认为,无论是从学生“学”的角度,还是从教师“教”的角度来看,都应化“被动”为“主动”,达到“教”与“学”的完美结合,在具体的教学实践中,笔者尝试从以下几个方面提高学生列方程解决问题的能力.
(一)自主调整,加强训练,培养代数意识
方程知识是“数与代数”领域的重要内容,而用字母表示数和列代数式则是掌握方程知识的基础,因此培养学生良好的代数意识非常重要. 列代数式就是把文字语言转变成数学语言,如桌子的单价是椅子的单价(用a表示)的3倍少14元,用代数式表示桌子的单价是3a - 14. 北师大版教材“用字母表示数”这一内容只安排了一个课时,笔者认为教学的内容需要教师做适当的调整,把列代数式作为基本训练. 提高了学生列代数式的能力,列方程解决问题就会迎刃而解.
(二)及时解释,巩固方法,明确“用等式性质解方程”的现实意义
新教材利用等式的性质解方程,学生不适应,内心排斥,特别是在初学解简易方程时,如在解5 + x = 24,x - 30 = 75这类简易方程时,学生一致认为等式性质的方法复杂,书写烦琐,为什么把简单的问题想复杂呢?笔者认为教师有必要在学生初学方程时就作出必要解释“为什么要用等式的性质解方程”. 记得上海的曹培英老师曾经写过一篇文章,专门就“用等式的性质解方程”这个问题解答了老师和同学们的困惑,他认为用等式的方法解方程首先是中小衔接的需要,进入中学后,学生将会用更多等式的性质解方程,为了促进学生学习的正迁移,达到中小学思路一致,所以我们用这样的方法解方程. 如果教师及时向学生作出解释,相信学生也能理解其中的现实意义和长远意义,正所谓“知其然而知其所以然”. 学生只有了解这一方法的来龙去脉,才会心甘情愿地接受此方法;在明确方法的情况下,千方百计地巩固此方法.
(三)总结规律,概括提升,掌握列方程解题的“小窍门”
总结方法,应用方法,并且概括提升是数学教学的基本要求. 在教学解方程时,教材都是根据实际问题,通过分析数量关系列出方程,再引导学生探索并掌握方程的解法. 这样既使学生体会到方程是解决实际问题的需要,又能使学生认识到列方程需要依据数量之间的相等关系. 教材中安排的实际问题是需要逆向思考的问题,学生经过列方程解决这样的实际问题,体会到列方程解决实际问题可以按条件的叙述顺序,通过正向思考解决. 因此,在平时的教学工作中,笔者让学生在充分感知基础上发现和概括了列方程解题的四个步骤:1. 弄清题意,找出未知数,用字母x表示;2. 找出问题中数量之间的等量关系;3. 列出方程;4. 解方程;5. 检验. 在这样一个“小窍门”的指导作用下,学生列方程解题的思路相对比较清晰,正确率也相对提高.
(四)算式与方程,对比练习,提高列方程解题意识
在学习了列方程解决问题后,教师应有意识地组织学生进行算术与方程的对比练习,通过比较练习,判断怎样的问题需要列方程解答,怎样的问题用算式就可以解答了.比如:一个数与它的3倍多6是48,这个数是多少?很明显这是一个逆向思维的问题,适合用方程解:“解:设一个数为x,3x + 6 = 48.”对比题:甲数是15,乙数是它的4倍多12,乙数是多少?列式为15 × 4 + 12;又如前面检测题中的第④题:某商场9月份的营业额是480万元,比8月份增加了,商场8月份的营业额是多少万元?(列方程:设8月份的营业额是x万元,x + x = 480)与它的对比题:某商场9月份的营业额是480万元,10月份比9月份增加了,商场10月份的营业额是多少万元?(列式为:480 + 480 × )通过这样的题型对比练习,形成一定模式,以后遇到问题就会想到它是否适合用方程解. 另外,教师还可以再精心选择一些数量关系更复杂的题目,让学生体会用方程解的便捷,体验方程的魅力,从而提高学生用方程解题的意识和能力.
总之,提高学生列方程解决问题的意识和能力,既不是一朝一暮的事,也不是一蹴而就的事,需要教师寻找“症结”,“对症下药”,方能化学生的“被动学”为“主动学”.

