数学方法论中“化归法”的教学反思
闫洁

【摘要】 “数学方法论”中的“化归法”,是一种十分行之有效的教学手段,但是在实践时,“化归法”又需要教师对化归的概念有较清晰的理解,对操作过程有较详实的记录 ,对结果有较客观的评述和总结. 数学的教学本身强调的不仅仅是拔高学生的解题能力,还意在培养学生对知识有真正完整的、成体系的理解和掌握. 在课堂的教学实践中,如何巧妙设计本节的化归着手点,如何让教学程序在教师的引导下有序展开,如何让学生真正理解和喜爱数学知识,是需要教师不断进行学情分析、知识解析和自我剖析的.
【关键词】 数学方法论;化归法;教学反思
据说数学家波利亚也曾有过和“化归”思想相关的烧水趣闻:一个煤气灶,一个水龙头,一盒火柴,一个空水壶,如何烧开一满壶水?物理学家觉得应该打开水龙头,将装有半壶水的壶灌满,再放到煤气灶上,用火柴点燃煤气灶把水烧开. 但数学家的回答是:先把装了半壶水的水壶倒空,然后去放在水龙头下灌满水,再放在炉上,将水烧开,因为这样才是“将新问题化归为熟知的旧问题”. 如此类似的趣闻还有欧拉的七桥问题,据说是在普雷格尔河中有两个岛、七座桥,如何能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到同样的出发点. 大数学家欧拉把桥简化为线,大地简化为点,但由于“通过交点的曲线总是偶数条”的论断,故“一笔画完”是不可能实现的数学问题,也就是在现实中不可能实现的实际问题.
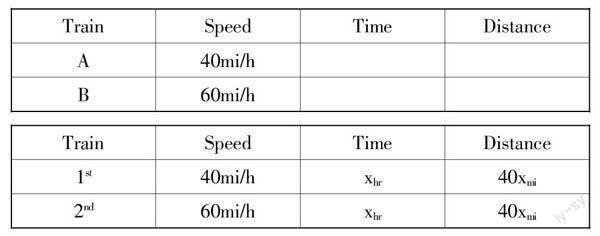
化归的思想就是如何能够把实际的题目转化为数学的题目,再把数学的题目转化为纯代数的题目,继而把纯代数的题目转为简单的解方程的过程. 文章首先是介绍了本节课所需用的若干概念定义,然后带领学生反复梳理最简单最经典的公式:Distance = Speed * Time,以及一些简单的“已知路程和时间求速度”“已知速度和时间求路程”以及“已知路程和速度求时间”的题目,让学生们感知“if we know two variables in this equation, it will be easy to find the 3rd variable”. 然后给出化归的初始步骤:列表,把所有已知条件全部填空进去(见下图).
这是初始的一步,也是十分简单易操作的一步,学生仅仅需要把应用题中的数字摘出来填入表格内即可,大家普遍表示“this step seems like easy”. 然后教师提醒大家关注time of train A和time of train B 之间的联系(学生们很快回复说the two trains will start at the same time and also meet with each other at the same time which means the time of A equals to the time of B),这时就可以把表格充实为下表. 那么此时就十分自然地推导出表中最后一列应该是来源于同行的左边两格的乘积,也就出现了“40x”和“60x”两个路程量,此时进一步询问学生:“What is the relationship between the two distances?”学生们稍迟疑后表示“their sum equals to 200mi”,然后问题就迎刃而解了. 这里是一个把“应用题化归为表格填空题再化归为解方程继而得到原题的解”的过程.
数学方法论中的化归法能够在一定程度上帮助教学工作者优化课堂授课效果,但其实施需要任教者和受教者的完美配合,需要避免课堂中的低效现象,更需要教师把握好“课前设计——课中调整——课后反思”的环节,让学生的认知能够得到尽可能完善的充实和完善.
【参考文献】
[1]章士藻,段志贵,陈汉平.数学方法论简明教程[M].南京:南京大学出版社,2008.
[2]徐利治.浅谈数学方法论[M].大连:大连理工大学出版社,2009.
[3]笛卡尔.笛卡尔思辨哲学(新版)[M].九州出版社,2004.

