从一中考试题学习中位线的应用
刘建辉
在几何解题过程中,中位线是一条非常有效的辅助线. 而在日常的教学中,曾多次利用中位线解决过一些问题. 假若在一些几何问题的解决中,能够联想到中位线并且利用好中位线,往往可以起到事半功倍的效果. 同时由于中位线这一辅助线在很多时候又难以想到,则更显弥足珍贵. 因而觉得在中考备考的综合复习时,有必要和学生共同探究这一辅助线的应用,借此提高学生自我总结能力,达到掌握一定的数学方法,同时提高自身的解题能力的目的.
在每年中考试题中不乏一些好题,它体现了某一种数学思想方法的应用,我们可以应用这些真题指导我们的复习备考,也可以提高学生的参与意识,在此,2009年河北省中考第24题给我们提供了一个很好的范例.
一、真题欣赏
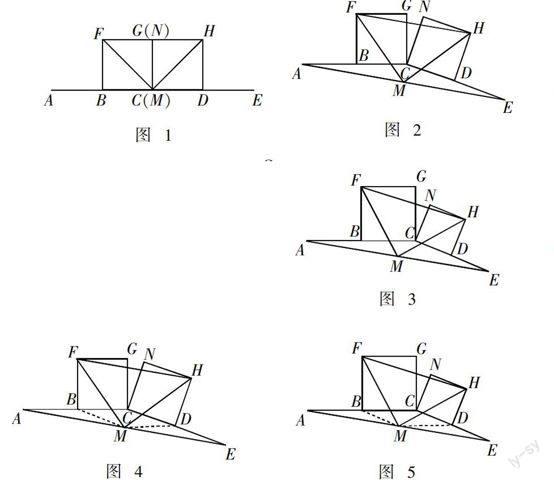
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点,四边形BCGF和CDHN都是正方形,AE的中点是M.
(1)如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,求证:FM = AH,FM⊥MH.
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,求证:△FMH是等腰直角三角形.
(3)将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必说明理由)
二、 解题分析
要完成这个问题的解答,我们应采用什么方法?观察题目条件,发现多个中点,联想中点辅助线的几种作法:(1)中线或过中点的线段延长加倍;(2)连接中点,形成中位线. 引导学生能够想到利用中位线去解答问题.
解:(1)比较简单,省略.
(2)如图4,连接MB,MD,设FM与BC交于P点. ∵ B,D,M分别是AC,CE,AE的中点,
∴ MD∥BC且MD = BC = BF,MB∥CD且MB = CD = DH.
∵ AC = CE,∴四边形BCDM是菱形.
∴ ∠CBM = ∠CDM.
∵ ∠FBP = ∠HDC,∴ ∠FBM = ∠MDH.
∵ △FBM ≌ △MDH,
∴ FM = MH,∠MFB = ∠HMD.
∵ ∠FMH = ∠FMD - ∠HMD = ∠APM - ∠MFB = ∠FBP = 90°,
∴ △FMH是等腰直角三角形 .
(3)原题并未对这一问题要求证明,非常遗憾,有种“买椟还珠”的感觉. 其实,这一问更能体现中位线在构造全等 三角形时的神奇作用. 因而在实际教学过程中要求学生求解,以此加强学生对中位线的认识.
如图5,连接MB,MD,设FM与BC交于P点.
∵ B,D,M分别是AC,CE,AE的中点,
∴ MD∥BC且MD = BC = BF,MB∥CD且MB = CD = DH.
∵ AC ≠ CE,∴ 四边形BCDM是平行四边形.
∴ ∠CBM = ∠CDM.
∵ ∠FBP = ∠HDC,∴ ∠FBM = ∠MDH.
∵ △FBM ≌ △MDH,∴ FM = MH,∠AFB = ∠HMD.
∵ ∠FMH = ∠FMD - ∠HMD = ∠APM - ∠MFB = ∠FBP = 90°,
∴ △FMH是等腰直角三角形 .
比较第(2)问和第(3)问,在第(2)问中四边形BCDM是菱形,△FBM和△MDH都是等腰三角形,无须考虑边的对应关系,而在第(3)问中,四边形BCDM是平行四边形,△FBM和△MDH不是等腰三角形,需考虑边的对应关系. 这正体现了中位线的价值.
三、方法提炼
在这个中考题的解答中,我们很好地利用了中位线,从而使问题顺利解决. 那么,需要我们思考在什么条件下需要“中位线”?“中位线”的作用和价值是什么?当问题中出现具有公共端点的线段的一个中点或多个中点时,或者是需要构造全等三角形时,我们可以考虑构造中位线,完成线段位置和大小的转移.
构造中位线有两大作用:(1)中位线完成线段的位置转移并能构造线段之间新的相等关系,为构造全等三角形做好准备;(2)中位线构造了平行关系,建立了新的角的相等关系,为构造全等三角形做好准备.
四、后 记
根据建构主义观点,“学习不是由教师把知识简单地传递给学生,而是由学生自己建构知识的过程. 学生不是简单被动地接收信息,而是主动地建构知识的意义,这种建构是无法由他人来代替的. ”在这里,教师和学生一起经历了方法的形成、方法的应用,教师和学生一起完成了这种方法的构建,而非教师一味地灌输. 经常有教师讲,这道题我讲过,这道题的方法我讲过,但学生就是不会. 原因何在?那就是我们没有和学生一起经历方法的形成过程. 借此也希望为即将到来的中考综合复习起到一个抛砖引玉的作用,让我们的学生能够真正地去总结数学方法,并把自己总结的方法应用到考试中去,取得优异的成绩.