平移与旋转在初中几何解题中的应用

传鹏

平移与旋转实际上是一种全等变换，由于具有可操作性，因而是考查同学们动手能力、观察能力的好素材，也就成了近几年中考试题中频繁出现的内容. 题型多以填空题、计算题呈现. 在解答此类问题时，我们通常将其转换成全等求解. 根据变换的特征，找到对应的全等形，通过线段、角的转换达到求解的目的.

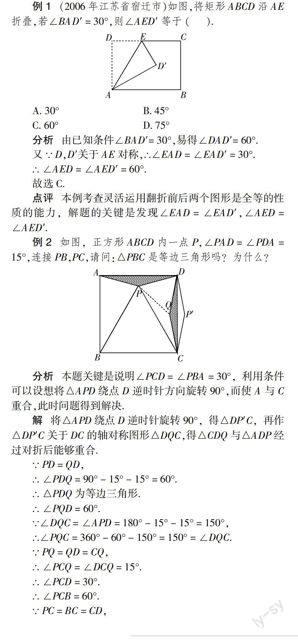
例1 （2006年江苏省宿迁市）如图，将矩形ABCD沿AE折叠，若∠BAD′ = 30°，则∠AED′ 等于 （ ）.

A. 30° B. 45°

C. 60° D. 75°

分析 由已知条件∠BAD′= 30°，易得∠DAD′= 60°.

又∵ D，D′关于AE对称，∴∠EAD = ∠EAD′ = 30°.

∴ ∠AED = ∠AED′ = 60°.

故选C.

点评 本例考查灵活运用翻折前后两个图形是全等的性质的能力，解题的关键是发现∠EAD = ∠EAD′，∠AED = ∠AED′.

例2 如图，正方形ABCD内一点P，∠PAD = ∠PDA = 15°，连接PB，PC，请问：△PBC是等边三角形吗？为什么？

分析 本题关键是说明∠PCD = ∠PBA = 30°，利用条件可以设想将△APD绕点D逆时针方向旋转90°，而使A与C重合，此时问题得到解决.

解 将△APD绕点D逆时针旋转90°，得△DP′C，再作△DP′C关于DC的轴对称图形△DQC，得△CDQ与△ADP经过对折后能够重合.

∵ PD = QD，

∴ ∠PDQ = 90° - 15° - 15° = 60°.

∴ △PDQ为等边三角形.

∴ ∠PQD = 60°.

∵∠DQC = ∠APD = 180° - 15° - 15° = 150°，

∴∠PQC = 360° - 60° - 150° = 150° = ∠DQC.

∵ PQ = QD = CQ，

∴ ∠PCQ = ∠DCQ = 15°.

∴ ∠PCD = 30°.

∴ ∠PCB = 60°.

∵ PC = BC = CD，

∴ △PBC为等边三角形.

例3 如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD = 2，BC = 3，将腰CD以D为中心，逆时针旋转90°至ED，连接AE，CE，则△ADE的面积是 （ ）.

A. 1 B. 2 C. 3 D. 不能确定

分析 解题的关键是求△ADE的边AD上的高. 可先求作直角梯形的高DF，想到将△CDF绕D逆时针旋转90°至△EDG，由EG = GF，只要求出CF的长，就可以求出△ADE的面积.

解 过D作DF⊥BC于F，过E作EG⊥AG，交AD的延长线于G.

∵∠B = 90°，AD∥BC，

∴四边形ABFD为矩形.

∴ FC = BC - AD = 3 - 2 = 1，∠EDC = ∠FDC = 90°.

∴ ∠FDC = ∠EDG. 又∵ ∠DFC = ∠G = 90°，ED = CD，

∴ △EDG ≌ △CDF. ∴ EG = CF = 1.

∴ △ADE的面积 = ■AD·EG = ■ × 2 × 1 = 1.

因此，选择A.

点评 明确△ADE的边AD上的高的概念不要误写成DE，作梯形高是常见的解题方法之一.