基于有功备用的风电机组一次调频能力及调频效果分析

李生虎，朱国伟

(合肥工业大学电气与自动化工程学院，安徽合肥230009)

基于有功备用的风电机组一次调频能力及调频效果分析

李生虎，朱国伟

(合肥工业大学电气与自动化工程学院，安徽合肥230009)

变速风电机组采用超速和变桨调节实现有功备用，通过下垂控制增发有功出力，可参与电网一次调频。基于风机出力对频率变化的增量，定义有无风电调频下的稳态频率偏移之差，以量化风电机组对减小频率偏移的贡献。发现风电调频能力与风电容量比例、风能大小、减载水平有关，调频效果与同步机组频率响应特性和电网负荷增量有关，确定了充分利用风电备用容量的负荷临界增量。稳态和动态仿真结果验证了不同风速下有功备用风电机组对电网频率的调节作用，发现高风速下风机动态过渡过程要比中低风速时快速。

一次调频;频率偏移;有功备用;变速风电机组;风电系统

1 引言

风电功率波动影响电力系统频率稳定［1］。随着风电容量增加，除了保证在故障时风电机组及电网安全［2-4］，也有必要使风电机组储备有功备用容量，协助电网频率调整［5］。

变速风电机组(双馈式和直驱式)的调频技术包括模拟惯量控制、下垂控制和协调控制［6］。模拟惯量控制在频率变化时释放/储存转子动能，以降低频率偏移和最低频率点［7］，下垂控制依据频率变化调整风电机组有功出力。两者均模拟了同步机组频率响应特性［8］，但前者只能提供暂态频率支持，对稳态频率偏移无贡献。后者可调用机组有功备用容量，支持电网一次甚至二次调频［9］，对减小频率稳态下降有积极贡献。文献［10］提出的控制方案能有效施行，但非常依靠桨距角调节，机械磨损较大。文献［11］划分出不同风速模式，在低风速下使用超速控制，中风速下协同使用桨距角和超速控制，高风速时单独使用桨距角控制，有利于降低机械磨损，因此较为实用。

风电系统频率控制方案设计的前提，是定量分析风电机组调频能力。文献［12］应用平均系统频率模型，推导了多机系统中风电采用模拟惯量和阻尼控制时频率最低点的解析表达，分析了虚拟惯量和阻尼系数对频率最低值的提升作用。文献［13］使风电机组在参与调频时输出一个暂时性的恒定功率增量，并量化分析了此功率增量对应的等效惯性时间常数。文献［14］给出了风电机组使用惯量控制时，在调频过程中有功增量与调频可持续时间的对应关系。风电机组通过减载运行参与频率调整时，对减小系统频率偏移有着重要的贡献，而现有文献中未见相关定量分析的报道，因此有必要进一步探讨。

本文针对基于超速和变桨控制的风电调频策略，以有无风电调频两种情况下的稳态频率偏移之差为切入点，在风电有功备用容量的约束下，量化风电对于减小稳态频率偏移的贡献。进一步分析风电有效参与调频与电网负荷变化量的关系，确定风电能够提供最大频率支撑能力时对应的电网负荷临界变化量。

2 超速和变桨的控制策略

2.1 风机的减载运行

下垂控制需要有功备用［15］，即风电机组需减载运行。如图1所示，当以恒定百分比减载时，风电机组沿曲线DEC运行［9］。与之相对应，在最大功率追踪(MPPT)方式下，沿曲线BAC运行。

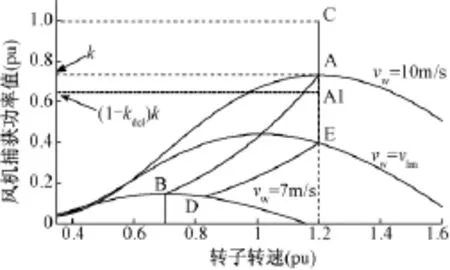
图1 风机捕捉功率与转速曲线Fig．1 Curves of power versus rotor speed of wind turbines

沿DE段运行时，风电机组仅依靠转子超速就能实现设定减载水平，桨距角保持在最小值(0°)，且此时E点对应的风速为vlm。在EA1段，由于转速已达上限，无法实现预期减载水平，需要依靠桨距角控制(如图2所示)进一步限制功率［11］。当运行在A1点时对应风速为vmh，这时最优转速恰好为转速上限。运行在A1C段时，转子超速已无法实现减载，只能依靠桨距角实现恒定减载。

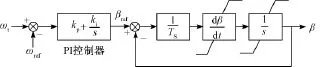
图2 桨距角控制框图Fig．2 Pitch angle control

图2中ωt和ωref为风机转速及其参考值，β和βref为桨距角及其参考值，kp和ki为PI控制参数，Ts为伺服时间常数，s为拉普拉斯算子。

2.2 各风速段下的调频控制策略

变速风电机组根据有功参考值Pref，通过电力电子变流器快速增发有功，在利用有功备用的同时释放转子动能，有助于扰动后电网频率恢复。

当电网频率变化Δf时，风电机组可以通过下垂控制增发有功ΔP，得到有功参考值Pref为:

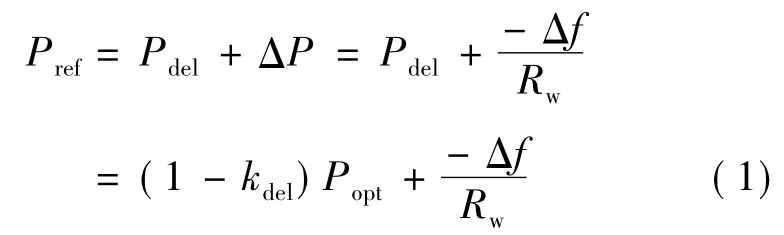
式中，Rw为下垂系数;Pdel为减载运行时的有功出力;kdel表示减载水平;Popt为相应风速下的最优捕获风功率。

文献［11］提出，针对不同风速段，可采用相应的控制策略:

(1)低风速段(vw≤vlm):电网频率下降时，可由Pref计算出对应的参考转速ωref，控制转子减速增大捕获风能。

(2)中风速段(vlm≤vw≤vmh):桨距角与超速控制同时起作用，因此参考转速可按式(2)获得［11］:

式中，ωopt为相应风速下最优转速;ωmax为转速上限。

(3)高风速段(vw≥vmh):由于转速达到上限ωmax，仅能依靠桨距角调节有功输出。此时转速参考值ωref保持为ωmax不变。

3 用于频率分析的电网机组模型

如图3所示，平均系统频率模型将发电机组的有功出力通过等值转子运动方程联系在一起。H∑为同步机组的惯性时间常数总和;D表征负荷频率恢复特性;ΔPm为同步发电机组的增发有功出力; ΔPwf为风电机组增发有功出力;ΔPL为有功负荷变化量;Kw为容量折算系数。

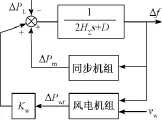
图3 包含风电的平均系统频率模型Fig．3 Average system frequency incorporating wind power

火电机组的原动机调速系统如图4所示［12］，Rm为下垂系数;Tg、Tch分别为各自一阶惯性环节的时间常数;ΔG为蒸汽阀门位置;Tr为再热时间常数; Fhp为功率系数，越小则调速动作越慢。

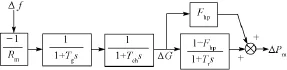
图4 火电机组原动机调速系统Fig．4 Governor system of thermal unit

4 风电对于减小稳态频率偏移的贡献分析

减载运行风电机组参与系统调频时，其对电网频率稳定性的贡献取决于机组有功备用容量。该备用容量与风机捕获风能大小、可用风电容量、减载水平等有关。当系统遭受不同程度的频率冲击时，风电对于电网频率的提升作用不同。

设系统中出现大小为ΔPL的有功缺额，由图3可得频率恢复稳态时，有:

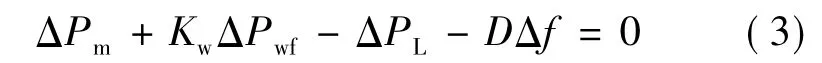
式中，火电机组的有功出力增量ΔPm为:

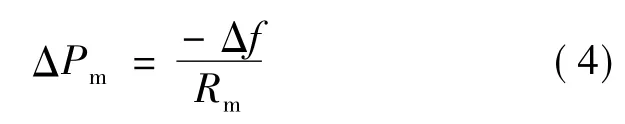
风电机组的增发有功ΔPwf与其最大有功备用余量有关，有如下关系:

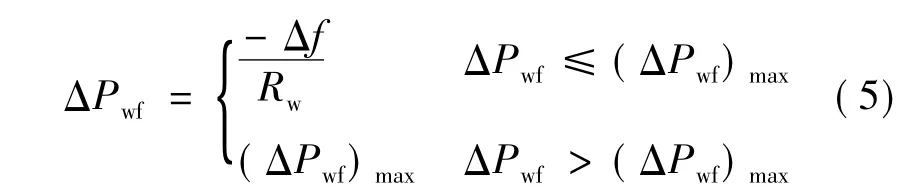
当ΔPwf处于风电机组有功备用余量可调用的范围内，这时风电机组能够有效地参与调频;否则释放全部有功备用后，不再继续参与频率调整，无法阻止频率继续跌落。

定义风电机组能够有效应对的最大稳态频率偏移量为|Δf|max，则:

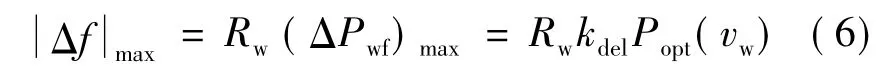
式中，风速vw下的最大捕获风功率标幺值Popt(vw)可进一步表达为:

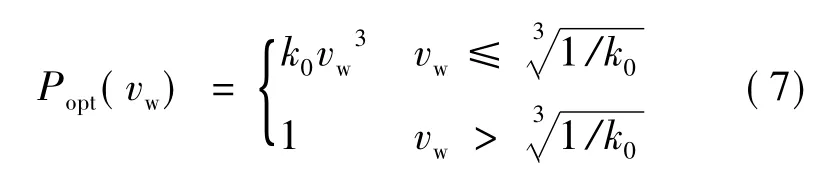
式中，系数k0可以写成以下形式:

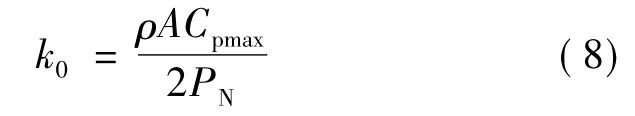
式中，ρ为空气密度;A为风轮叶片扫过的面积;PN为风电机组额定功率;Cpmax为最大风能捕获系数。于是|Δf|max可以由式(6)～式(8)表达为:

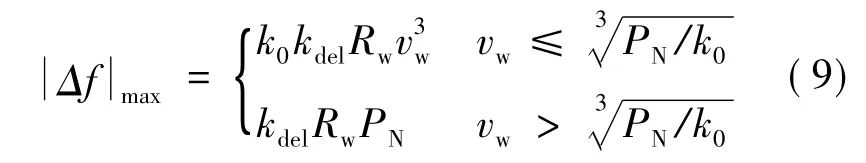
值得说明的是，由于最大功率跟踪曲线的转速恒定区域对应的风速区间很窄，因此在式(9)对频率变化的估计中忽略了这一部分的影响。由式(9)可知，|Δf|max与风机的减载水平kdel和选取的下垂系数Rw有关，当风机可捕获的最大功率小于额定功率PN时还与风速vw有关。

由于负荷增加ΔPL导致系统出现的稳态频率偏移量大小记为|Δf1|，而风电不参与调频时，相应频率偏移记为|Δf0|。定义两者之差为

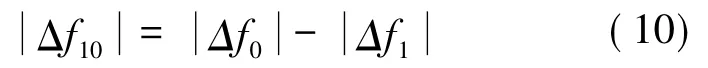
|Δf10|反映了风电调频对于电网稳态频率的提升作用。下面给出|Δf1|和|Δf0|的具体表达形式。当|Δf1|≤|Δf|max时，由式(3)～式(5)得到:

当|Δf1|＞|Δf|max时，得到:

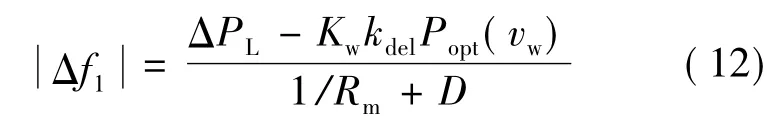
对于|Δf0|则有:

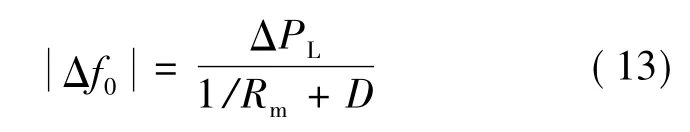
由式(11)～式(13)可以得到ΔPL与Δf的关系如图5所示，其中slope为斜率。对应|Δf|max，存在临界负荷变化量ΔPL0，使得当ΔPL≤ΔPL0时，|Δf10|随着ΔPL的增大而增大，说明风电调频对于系统稳态频率的提升更加明显;而当ΔPL＞ΔPL0时，|Δf10|为一定值，与ΔPL的大小无关，说明风电调频对于频率提升的作用已经饱和。

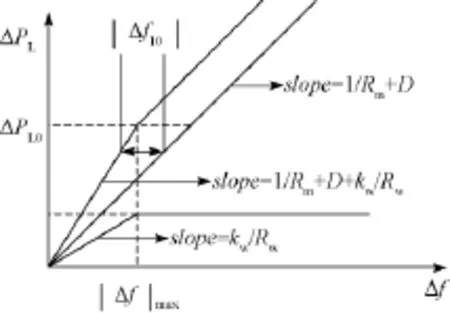
图5 ΔPL与Δf的变化关系Fig．5 Relations between ΔPLand ΔfV

由式(6)和式(11)可得ΔPL0的表达式为:

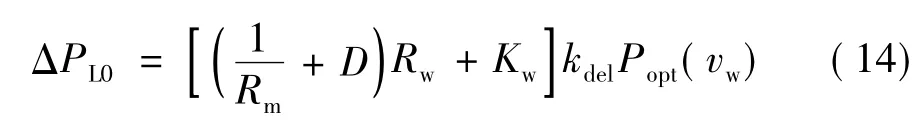
风电调频对于电网稳态频率的最大提升为:

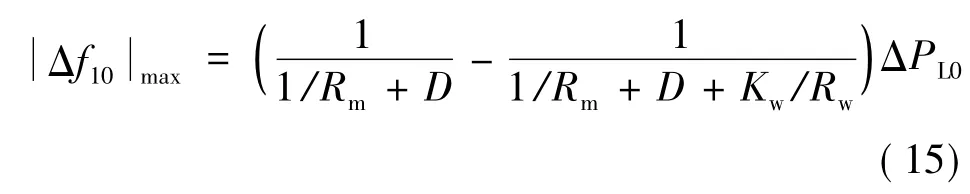
式(15)进一步化简为:

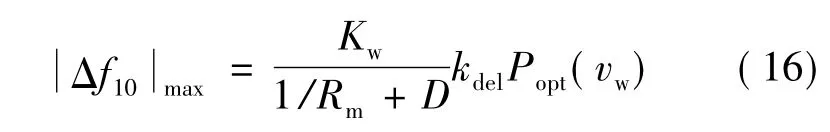
综合式(14)、式(16)来看，与火电机组具有充足旋转备用不同，风电机组有功备用容量有限，这成为制约其一次调频能力的主要因素，但现有文献缺少该方面的定量分析。式(14)给出了电网负荷增量与风电调频能力之间的关联，即当风电机组运行状态(如减载水平kdel、风能大小)和控制参数(如下垂系数Rw)确定时，超出临界负荷变化量将会使用全部的风电有功备用。式(16)进一步说明，评估风电调频效果不是直接考察稳态频率偏移的绝对值，而是应关注于风电参与调频带来的最大频率提升值，后者更具一般意义。

5 算例分析

5.1 量化风电对一次调频的贡献

给定风电机组下垂系数Rw为0.05，风电容量比例Kw为0.4，即可算出不同风速下ΔPL0和|Δf10|max，结果如表1所示。本文5.2节将以表1中计算出的临界负荷变化量为参考，设置合适的负荷变化量进行仿真分析。

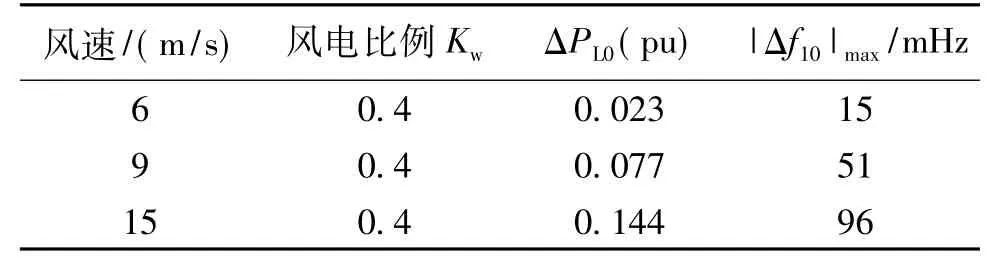
表1 各风速下对应的ΔPL0和|Δf10|maxTab．1 ΔPL0and|Δf10|maxunder different wind speeds

5.2 不同风速下风电调频效果分析

以下给出动态仿真结果，以验证第4节稳态调频算法的正确性。设风电机组稳态运行，在t=0.5s时刻负荷突然增大，变化量为ΔPL=0.05pu(中低风速段)或0.10pu(高风速段)。

(1)低风速

取vw=6m/s，图6(a)给出风电调频效果，风电参与调频更加明显地提升电网(Fhp=0.3)频率最低点。

图6(b)反映了调频过程中风电机组输向电网有功和捕获风功率的变化。由于低风速下风电机组捕获的风能较小，因此在相同的减载水平下拥有更少的有功备用。当系统频率降低时，风机转子需要依靠电磁转矩和机械转矩之间较小的转矩不平衡量来驱使转速降低，整个过程近似一阶惯性响应，没有超调但是需要较长的时间过渡到新的稳定运行点。从表1可以看出，风电机组有效参与调频时对应的临界负荷变化量为0.023pu，小于仿真中的0.05pu，因此机组使用了全部的减载有功备用，使稳态频率偏移提升了0.015Hz。

(2)中风速

取vw=9m/s，如图7(a)和图7(b)所示，与低风速时相比，在相同负荷变化量下稳态频率偏移提升了0.03Hz左右，同时风机还留有部分备用可以进一步参加二次调频。

图7(c)和图7(d)分别表现了转子转速和桨距角的变化情况。当系统频率降低时，希望通过立即降低转速和桨距角来最大程度地释放风电机组的有功备用，而从转速控制(式(2))和变桨控制(图2)来看，参考转速降低导致桨距角PI控制器产生一个正值的输入信号，导致桨距角参考值增大。因此桨距角首先会增大，与期望的动作方向相反，这样延长了过渡所需要的时间，桨距角和转子转速在经历了超调后逐渐恢复稳定。

图6 低风速时的风电调频效果Fig．6 Frequency regulation with low wind speed

(3)高风速

取vw=15m/s，结果如图8所示，此时风电参与调频使电网能够应对更大的有功不平衡量。如图8 (a)所示，在负荷增加0.10 pu时稳态频率偏移提升0.07Hz左右。对调速相对较慢的电网，频率最低点提升达240mHz，且在调频过程中风电机组暂时性地使用了全部的有功备用，如图8(b)所示。

图8(c)和图8(d)反映了转子转速和桨距角的变化情况。对比发现，当变桨响应时间从0.5s增大至1.5s，其他参数保持不变时，动态过程出现振荡，但是如果桨距角PI参数设置得当，相对充足的有功备用能够通过快速变桨控制被迅速地释放出来，因而动态过程仍比中低风速下要快很多。

6 结论

本文研究了减载运行风电机组通过超速和变桨控制参与电网一次调频的特性，量化其调频能力和调频效果，得到以下结论:

(1)相对于直接考察风电参与调频时电网的稳态频率偏移，有无风电调频两种情况下的稳态频率偏移之差更能反映风电对于频率调整的贡献。

(2)考虑风电实际具有的有功备用容量大小，风电只能在一定范围内有效参与调频。当电网负荷达到某一临界变化量时，风电能提供最大程度的有效频率支撑作用。

(3)在风电参与调频过程中，高风速下仅依靠桨距角调节有功出力，风机能很快过渡到新的稳态运行点;中风速下由于同时控制转速和桨距角，动态过渡过程较长;低风速下作用在风机转子上的转矩不平衡量很小，因此也需要较长时间过渡到新的平衡点。

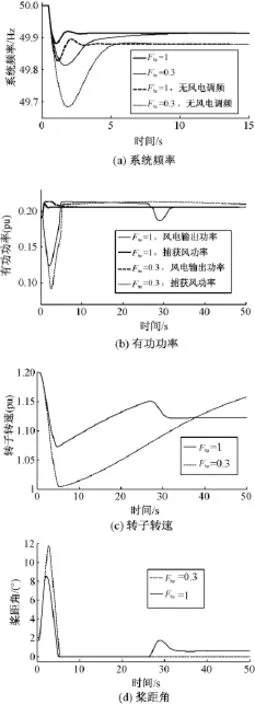
图7 中风速时的风电调频效果Fig．7 Frequency regulation with medium wind speed

图8 高风速时的风电调频效果Fig．8 Frequency regulation with high wind speed

附录:

(1)风力机数据:额定容量PN=2MW;空气密度ρ=1.225kg/m3;风轮半径为39.8m;风轮基准转速为 1.6978 rad/s;惯性时间常数为 2s;Cpmax= 0.48。

(2)桨距角控制数据:桨距角变化率范围为±5°/s;桨距角启动范围为0～27°;伺服时间常数为0.5s;PI控制参数为kp=100，ki=40/s。

(3)火电机组数据:额定容量为5MW;原动机调速系统中时间常数Tg=0.1s，Tch=0.25s，Tr=5s;功率系数Fhp=1;下垂系数Rm=0.05;惯性时间常数3s。

(4)其他:系统基准容量(与火电机组额定容量相同)为5MW;负荷频率恢复特性系数D=0.8;风电机组的功率转换系数Kw=2MW/5MW=0.4;下垂系数Rw=0.05。

［1］Sun Y Z，Zhang Z S，Li G J，et al．Review on frequency control of power systems with wind power penetration ［A］．IEEE 2010 International Conference on Power System Technology［C］．Hangzhou，China，2010.1-8．

［2］岳涵，郑宽，于洋，等 (Yue Han，Zheng Kuan，Yu Yang，et al．)．大规模双馈风电接入对东北电网稳定性的影响(Impact of large-scale DFIG based wind power on stability of northeast power grid)［J］．电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2013，32(4):1-6．

［3］孟明，靖言，李和明，等 (Meng Ming，Jing Yan，Li Heming，et al．)．变速恒频直驱型风电系统低压穿越技术 (Low voltage ride through technology for variablespeed constant-frequency direct-drive wind power systems)［J］．电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2011，30(2): 53-58．

［4］吴俊玲，吴畏，周双喜，等 (Wu Junling，Wu Wei，Zhou Shuangxi，et al．)．超导储能改善并网风电场稳定性的研究(Study on SMES unit for improving the stability of power system connected with wind farms)［J］．电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2004，23(3):59-63．

［5］Ackermann T．风力发电系统 (Wind power in power systems)［M］．谢桦，王健强，姜久春 (Xie Hua，Wang Jianqiang，Jiang Jiuchun)译．北京:中国水利水电出版社 (Beijing:China Water＆Power Press)，2010．

［6］刘巨，姚伟，文劲宇，等 (Liu Ju，Yao Wei，Wen Jinyu，et al．)．大规模风电参与系统频率调整的技术展望 (Prospect of technology for large-scale wind farm participating into power grid frequency regulation)［J］．电网技术(Power System Technology)，2014，38(3): 638-646．

［7］唐西胜，苗福丰，齐智平，等 (Tang Xisheng，Miao Fufeng，Qi Zhiping，et al．)．风力发电的调频技术研究综述 (Survey on frequency control of wind power) ［J］．中国电机工程学报 (Proceedings of the CSEE)，2014，34(5):4304-4314．

［8］Rahmann C，Moller R，Salles M B C．Frequency stability support requirements for WTs in slow-response thermal power systems［A］．IEEE Power and Energy Society General Meeting［C］．Vancouver，BC，Canada，2013. 1-5．

［9］吴子双，于寄来，彭喜云 (Wu Zishuang，Yu Jilai，Peng Xiyun)．高风速段次优功率追踪方式的风电调频方法 (DFIG’s frequency regulation method only for high wind speed with suboptimal power tracking)［J］．电工技术学报 (Transactions of China Electrotechnical Society)，2013，28(5):112-119．

［10］de Almeida R G，Peas Lopes J A．Participation of doubly fed induction wind generators in system frequency regulation［J］．IEEE Transactions on Power Systems，2007，22(3):944-950．

［11］张昭遂，孙元章，李国杰，等 (Zhang Zhaosui，Sun Yuanzhang，Li Guojie，et al．)．超速与变桨协调的双馈风电机组频率控制 (Frequency regulation by doubly fed induction generator wind turbines based on coordinated overspeed control and pitch control)［J］．电力系统自动化 (Automation of Electric Power Systems)，2011，35(17):20-25．

［12］Akbari M，Madani S M．Analytical evaluation of control strategies for participation of doubly fed induction generator-based wind farms in power system short-term frequency regulation［J］．IET RenewablePowerGeneration，2014，8(3):324-333．

［13］Ullah N R，Thiringer T，Karlsson D．Temporary primary frequency control support by variable speed wind turbines-Potential and applications［J］．IEEE Transactions on Power Systems，2008，23(2):601-612．

［14］何成明，王洪涛，孙华东，等 (He Chengming，Wang Hongtao，Sun Huadong，et al．)．变速风电机组调频特性分析及风电场时序协同控制策略 (Analysis on frequency control characteristics of variable speed wind turbines and coordinated frequency control strategy of wind farm)［J］．电力系统自动化 (Automation of Electric Power Systems)，2013，37(9):1-6．

［15］李生虎，孙莎莎，王正风 (Li Shenghu，Sun Shasha，Wang Zhengfeng)．旋转备用下双馈风电机组初值算法(Initialization method of DFIG-based wind power units with spinning reserve)［J］．电力系统自动化 (Automation of Electric Power Systems)，2013，37(11):7-12．

(，cont．on p.50)(，cont．from p.33)

Capability and effect of primary frequency regulation by wind turbine generators with active power reserve

LI Sheng-hu，ZHU Guo-wei
(School of Electrical Engineering and Automation，Hefei University of Technology，Hefei 230009，China)

Variable-speed wind turbine generators may operate with active power reserve by overspeed and pitch angle control，thus it is possible to participate in primary frequency regulation following droop control．Based on active output increment of the wind turbines，difference between steady-state frequency deviations without and with wind power frequency regulation is defined to quantify contribution of the wind turbine generators to decrease frequency deviation．It is found that the frequency regulation capability is decided by the wind power penetration，the captured wind power and the deloading level，while the regulation effect is decided by the frequency response of the synchronous generators as well as the load increment of the power systems．The critical load increment fully utilizing the active power reserve of the wind turbines is determined．The steady-state and the dynamic simulations verify frequency regulation effect under different wind speeds，and show that the dynamic process under high wind speed is quicker than those under medium or low wind speeds．

primary frequency regulation;frequency deviation;active power reserve;variable-speed wind turbine generator;wind power system

TM761.2;TM614

A

1003-3076(2015)10-0028-06

2014-11-07

国家自然科学基金资助项目(51277049)

李生虎(1974-)，男，安徽籍，教授，博士生导师，研究领域为电力系统规划与可靠性、风电系统分析与控制、柔性输电技术;朱国伟(1990-)，男，安徽籍，硕士研究生，研究方向为风电系统分析控制。