基于主从博弈的交直流混联系统主动防御策略设计

张振安，黄少伟，梁易乐，赵 阳

(1．国网河南省电力公司电力科学研究院，河南郑州410100; 2．电力系统及发电设备控制和仿真国家重点实验室，清华大学电机系，北京100084)

基于主从博弈的交直流混联系统主动防御策略设计

张振安1，黄少伟2，梁易乐2，赵 阳1

(1．国网河南省电力公司电力科学研究院，河南郑州410100; 2．电力系统及发电设备控制和仿真国家重点实验室，清华大学电机系，北京100084)

随着电网规模的扩大化与系统元件的复杂化，特别是交直流混联输电格局的逐步形成，系统安全稳定问题也日益严重。准确确定电网脆弱源，并制定相应防御策略以预防大停电事故的发生变得至关重要。本文针对交直流混联系统提出了主动防御策略制定的主从博弈模型，即D-A-D(防御者-进攻者-防御者)三层规划模型。上层模型制定电力系统防御策略，中层模型确定并发故障元件集合，而下层模型模拟系统故障后的安全调度过程。上述模型可先转换为下层为混合整数线性规划的双层模型，后采用枚举树算法求解。在IEEE30节点系统中进行仿真分析，验证了上述模型的合理性与有效性。

电力系统;主动防御;主从博弈;三层规划

1 引言

近年来，系统规模日益扩大以及系统元件复杂化成为电力系统发展的两大主要趋势，系统的安全稳定问题也随之产生［1-4］。特别是随着交直流混联输电的格局逐步形成，并联运行的交流与直流线路关联紧密，彼此间相互影响，系统运行特性也更为复杂。由电网局部故障波及整个网络造成的大规模停电事故，在国内外偶有发生，造成了严重的社会影响和经济损失。因此，在不能预知故障发生的情况下，准确地确定电网当前的脆弱源，并采取事故前主动防御措施，进而预防连锁故障的发生，是一项非常重要的研究课题。

安全博弈理论为上述问题提供了合适的研究手段。在该理论中，由自然原因或蓄意攻击导致的电网故障被视为攻击方，而系统相关部门被视为防御方。攻击方试图使系统元件并发故障而退出运行，最大化系统损失;而防御方则采取防御策略，增强系统安全裕度，降低系统故障损失。安全博弈及其均衡解可指导系统最优防御策略的制定，同时可用于辨识系统薄弱环节，合理评估系统运行的可靠性与脆弱性。一般而言，结合系统实际，攻防双方先后决策，符合主从博弈的一般过程，相应建模方法可分为以下三类:

(1)A-D(进攻者-防御者)模型

即进攻者先于防御者决策，属于典型的双层规划模型。可通过求解所得进攻者(A)的Stackelberg均衡策略用于辨识系统薄弱环节。

(2)D-A(防御者-进攻者)模型

即防御者先于进攻者决策，属于典型的双层规划模型。可通过求解所得防御者(D)的Stackelberg均衡策略指导系统防御策略的初步制定，但策略的最优性往往很难保证［5］。

(3)D-A-D(防御者-进攻者-防御者)模型

防御者、攻击者、防御者依次决策，属于典型三层规划模型。可通过求解所得防御者(D)的Stackelberg均衡策略解决系统在无法预料多重扰动的情况下，最优防御策略的制定问题。

采用上述主从博弈模型进行系统脆弱性评估以及防御策略制定的相关研究在国内还较为少见。在早期国外的研究中，A-D模型由于求解难度较低，常用于评估系统元件的关键程度，并基于所得结果进行防御策略的制定［6，7］。然而研究发现，直接对所得关键元件进行防护，往往并非最优防御策略［5，8］。此外，上述模型虽然考虑了相关部门所采取的调整措施对元件关键程度的影响，但调整措施在故障发生后才被动开展，对并发故障的抵御效果较差。而D-A-D模型可以弥补其不足，变传统“被动挨打”的安全防御部署模式为“主动出击”，有效降低系统损失。

文献［8-10］均尝试采用D-A-D模型指导最优防御策略的制定，即通过对有限资源的优化配置，合理选择系统中部分元件进行防御，以极小化故障造成的系统损失。然而受限于问题求解的难度，以上研究对于攻防双方的建模仍较为抽象。

本文在上述工作的基础上，针对交直流混联系统提出了主动防御策略制定的主从博弈模型，即DA-D模型。上层模型负责进行电力系统防御策略的制定，中层模型确定并发故障元件集合，而下层模型则模拟系统故障后的安全调度过程。同时在上层防御策略的制定过程中，考虑不同元件防护成本差异，使所得结果更具有参考价值。上述模型可先转换为下层为混合整数线性规划的双层模型，后采用枚举树算法求解。IEEE30节点系统的仿真结果验证了上述模型的合理性。

2 交直流混联系统主动防御策略制定的主从博弈模型

2.1 问题背景描述

电力系统相关部门与系统故障之间的主从博弈过程能够由D-A-D模型来刻画。该模型可自然反应电力系统相关部门的真实动作过程，具体分为以下三个阶段。

(1)第一阶段中，电力系统相关部门制定防御规划策略，对资源进行优化配置，选择系统中的关键元件进行重点防护，以降低故障带来的系统损失。具体的防御措施可以为备用元件的投入、安全监控设施的部署等。

(2)第二阶段中，自然原因或蓄意攻击导致电网多个元件同时故障。该故障元件集合试图极大化系统损失。

(3)第三阶段中，电力系统相关部门进行事故后潮流调整。由于直流线路传输功率具有可控性，因此相关调整手段可考虑为直流传输功率调节量ΔPd、发电机出力调节量ΔPg和负荷切除量ΔPld三种。

在实际电力系统中，上述三个阶段相互影响，各决策者间相互博弈满足自身优化目标。第一阶段的防御措施与第三阶段的安全调度过程均将影响系统元件的脆弱性分布，进而影响并发故障元件的确定。为了确保第一阶段防御措施的鲁棒性，应在第一阶段防御策略制定时考虑后续两个阶段的影响。

2.2 主从博弈模型

本节中使用的参数与变量如表1和表2所示。

表1 模型相关参数Tab．1 Parameters

基于2.1节分析，本文所提出的电力系统相关部门与系统故障之间的主从博弈过程可由D-A-D三层模型来刻画。其中，上层模型用于模拟系统主动防御策略的制定，即利用有限资源选择系统中元件进行防护;中层模型用于确定在当前防御策略下，同时退出运行后可对系统造成最大损失的元件集合;下层模型模拟故障后为维持系统正常运行，调度部门所进行的潮流调整。相应博弈结构图如图1所示。

下层模型的安全调度问题可采用基于直流潮流的OPF模型。由于面向交直流混联系统，因此需要在安全调度过程中考虑直流线路传输功率可控性对系统运行的影响。故该模型以直流传输功率调节量ΔPd、发电机出力调节量ΔPg、负荷切除量ΔPld作为系统潮流的调节手段。由于系统在安全正常运行状态下往往具有最小运行成本，并且考虑到直流系统的有功特性，即过高直流传输功率将增加系统运行风险，而过低直流传输功率有违经济性原则，该OPF模型以最小调整量作为目标函数［11］。通过控制成本系数wP-dk、wP-gi和wP-ldj的设置，该目标函数可用以表征故障后的系统损失。具体模型如式(1)～式(8)所示。

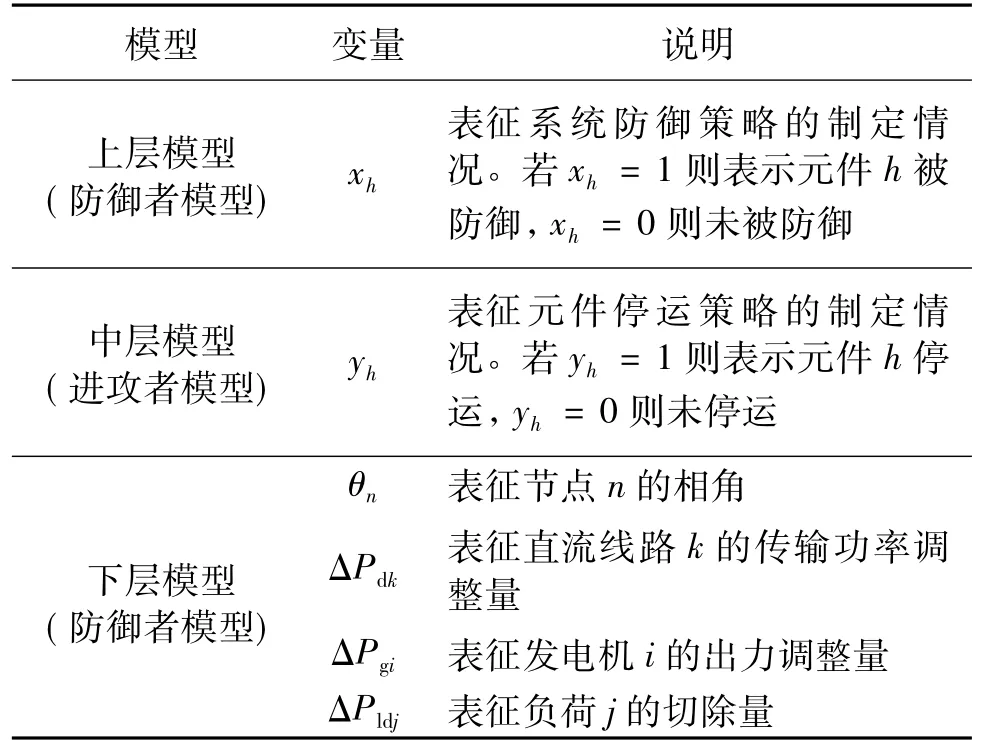
表2 模型决策变量集合Tab．2 Decision variables and vectors

图1 主从博弈模型结构示意图Fig．1 Structure of Stackelberg game

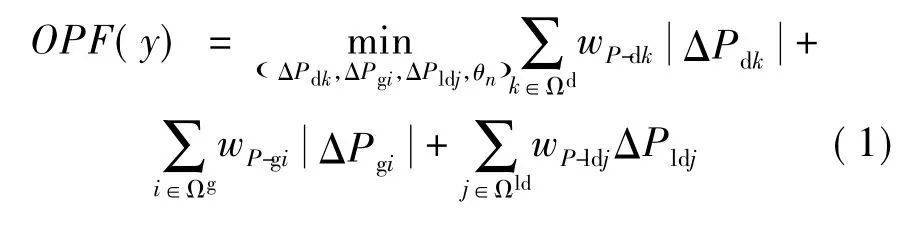
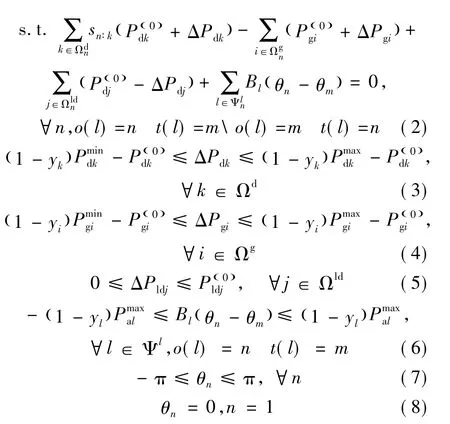
考虑到元件退出运行后的影响，上式分别对直流线路传输功率、发电机出力以及负荷切除量的上、下限进行修正。本文仅考虑直流线路、发电机、交流线路三类元件的停运问题。

上述目标函数中存在绝对值环节，此处采用文献［11］中方法，对目标函数进行线性化，进而得到模型如式(9)～式(23)所示。

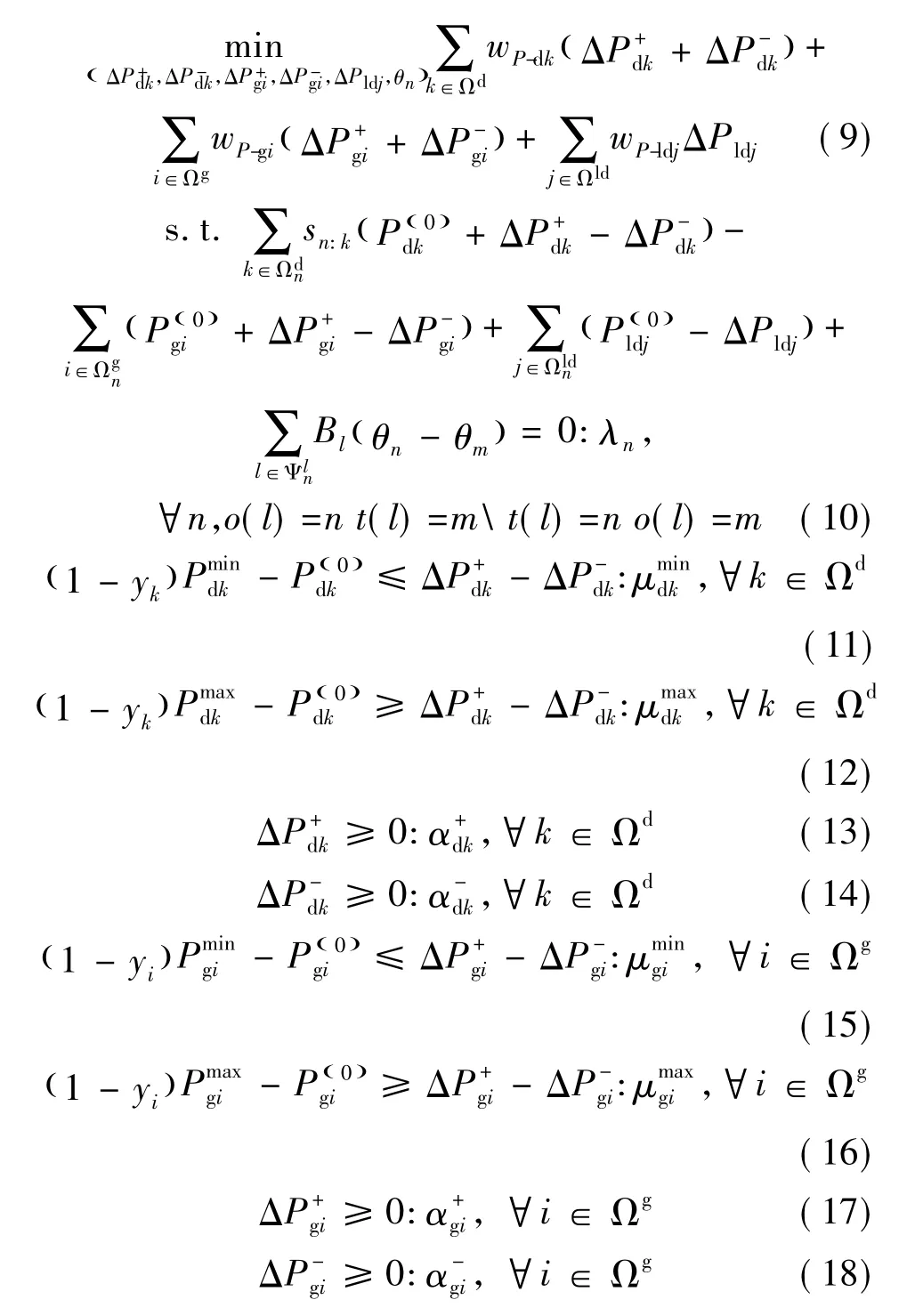
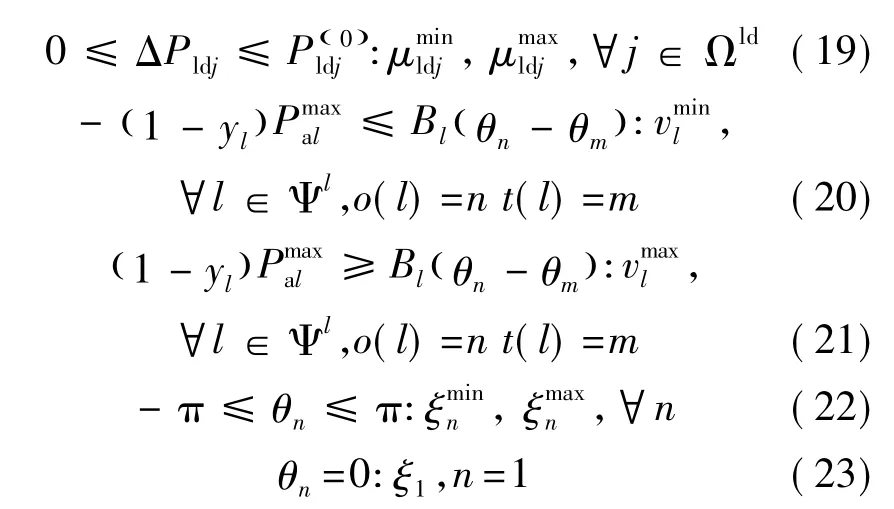
其中，各约束表达式的对偶变量列于相应式后。

中层模型通过确定总数为K的并发故障元件集合y，模拟电力系统事故，以极大化故障后系统损失。具体模型如式(24)和式(25)、式(9)～式(23)所示。

下层模型如式(9)～式(23)所示。

事实上，中层模型以下层模型为约束条件，二者间的主从博弈构成A-D(攻击者-防御者)双层优化问题。下层优化问题的变量为其中，对偶变量将在A-D双层模型式(24)和式(25)、式(9)～式(23)的等价混合整数线性规划中用到。中层优化问题的变量为此外，由于电力系统的安全调度发生在N-K校验之后，在下层模型中，元件停运决策列向量y作为给定参数处理，因此下层模型为线性规划问题。

在上层模型中，电力系统相关部门通过对有限资源Q的合理优化配置，进行主动防御策略的制定，即确定系统防御元件集合x。上层模型以中层模型为约束条件，二者构成D-A-D(防御者-攻击者-防御者)三层模型。具体模型如式(26)～式(30)、式(24)和式(25)、式(9)～式(23)所示。

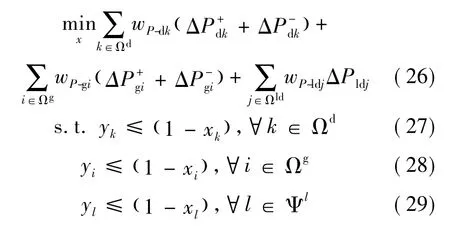
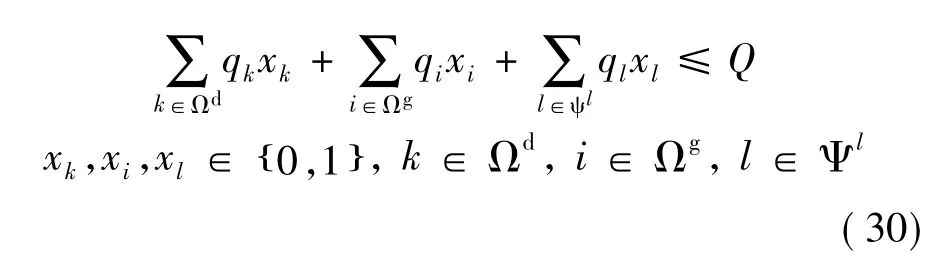
中层模型如式(24)和式(25)、式(9)～式(23)所示。本文假设元件被防御后就不再故障停运。

上述模型体现了电力系统相关部门与系统故障之间的主从博弈过程。

3 模型求解算法

主从博弈是一个三层优化问题，求解难度大。根据各层模型目标函数、约束条件以及变量类型等的不同，模型的求解方法也有所差别。文献［5］提出采用Benders分解方法对三层模型问题进行求解。文献［9］将原问题分解为两个嵌套的双层问题交替迭代求解。文献［8，10］均将求解过程分为两阶段，二者均先将中层与下层模型对应双层模型转化为单层，进而将原模型等价为一个下层为混合整数线性规划的双层优化问题;不同的是在后续双层问题求解上，文献［10］借鉴两阶段鲁棒优化问题的求解思路进行解算。而文献［8］基于模型变量与目标函数的特殊性采用枚举方法进行求解。本文基于文献［8，12］中的方法，对三层优化问题进行求解，求解过程同样可分为两个阶段。

3.1 等价双层模型转化:KKT最优性条件

该阶段求解转换过程针对中层与下层模型进行。首先，采用文献［13，14］中的方法，将下层优化问题用其相应KKT条件表征。由于下层模型为线性规划问题，因此该KKT条件为其达到全局最优性的充分必要条件。

将下层优化问题用其KKT条件表征，并根据文献［15］中的方法对互补松弛条件进行线性化处理，进而将式(26)～式(30)、式(24)和式(25)、式(9)～式(23)转化为传统的混合整数线性规划。

3.2 等价双层模型求解:枚举树算法

经过3.1节转换得到的双层模型，其下层为混合整数线性规划问题。注意到上层模型变量为0－1变量，且两层目标函数一致、博弈纯策略空间相同，可采用枚举方法进行求解。算法具体过程如下。

(1)生根策略

(2)生长策略

令xj=1，即对元件j进行防御，则求解下层模型，进而确定一系列新的故障元件集合y*(k+1)，同时令x(k+1)=x(k)∪{j}。新生子节点与父节点的树枝长度取决于相应选择元件所需防御资源数。

令xj=0，即不防御元件j，则从c(k)中重新选择其他元件i(i≠j)重复。新生子节点与父节点的树枝长度为0。若此时c(k)为空集，则称该节点为空防节点。

(3)判断终止策略

若当前节点距离根节点的树枝总长度等于限定防御资源总数，或剩余防御资源不足以展开进一步防御，则认为该节点为叶节点，不再生枝;否则令k =k+1，并重复上述生长策略，至所有节点均为叶节点或空防节点为止。

(4)最优防御策略确定

在得到的所有叶节点中，具有最小系统损失者即对应系统的最优防御策略，即系统的最优防御元件集合。

根据文献［12］，该算法可在有限步得到最优解，并且选择防御元件的先后顺序并不会影响最终结果，因为该算法会遍历所有可能的元件防御组合情况。

4 算例及其分析

本节以IEEE30节点系统为例进行仿真分析。此处将IEEE30节点系统中的交流线路4-6替换为直流线路，其中节点4为整流节点，节点6为逆变节点。考虑到系统实际情况，此处设置几类元件所需防御资源如下:

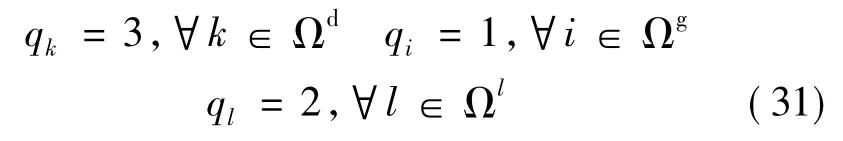
在安全调度模型中，设置控制成本系数wP-d= 5，wP-g=1，wP-ld=10，通过求解三层模型，可以得到系统在不同并发故障元件数下的最优防御元件集合，如表3所示。

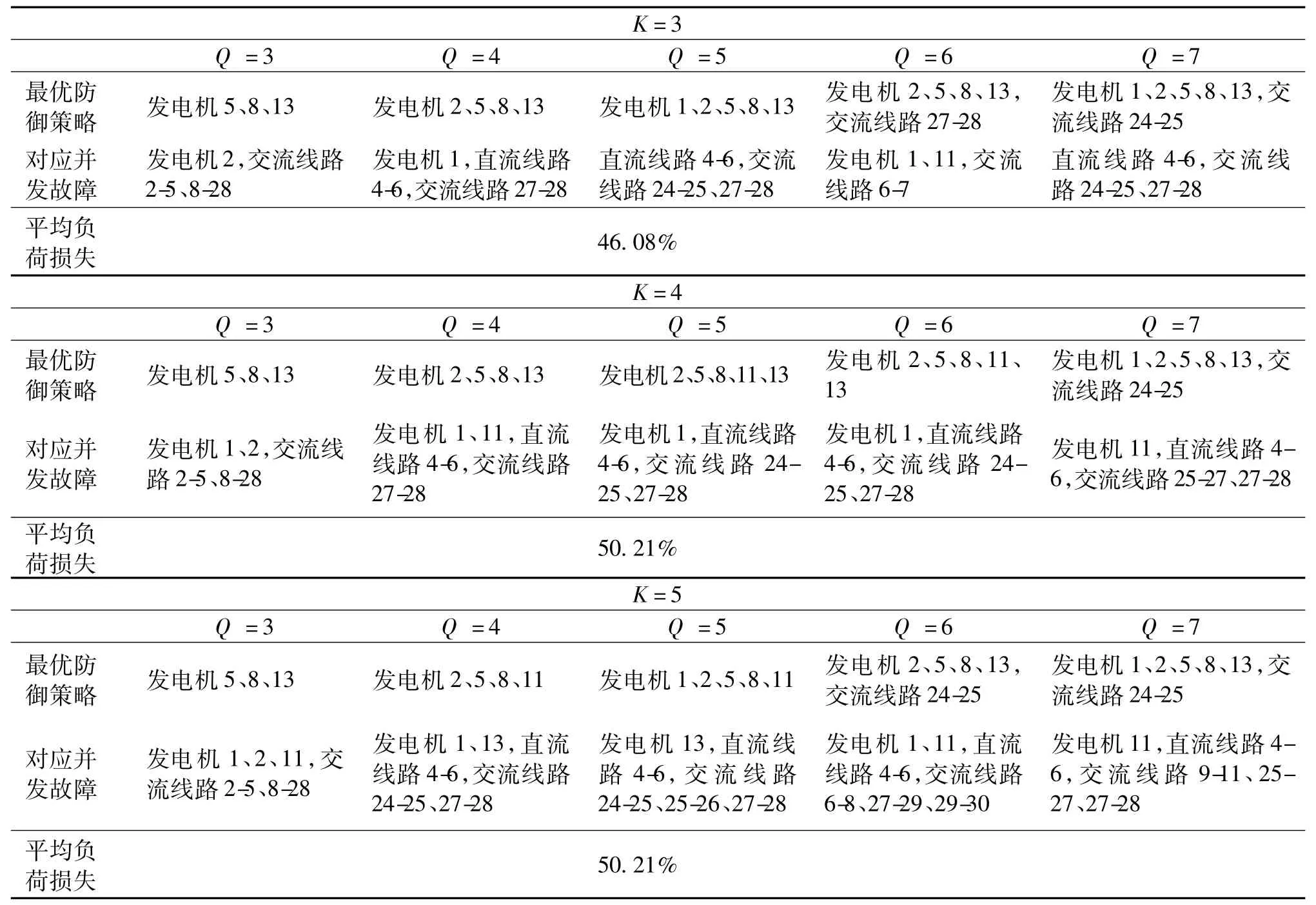
表3 最优防御策略集合及相关信息Tab．3 Optimal defense strategy and related information

通过表3可以看出，在不同并发故障数下，相较于无防御状态，在引入防御措施后，系统的失负荷量大大降低，有效地缓解了系统故障带来的影响。当系统防御总资源较少时，所需防御资源相对偏低的发电机往往被选择为防御元件。而随着系统防御总资源的增加，一些交流线路往往会被选作防御对象，如线路24-25、27-28。上述线路往往为电网末端与主体连接线路，开断后极易造成系统解列。从系统并发故障情况来看，发电机及相应出线、直流线路、电网末端与主网连线中，若出现多个并发故障，极易给系统带来较严重的损失。这与电力系统实际情况相符合，仿真结果表明了本文模型的合理性与有效性。

5 结论

本文针对交直流混联系统提出了一种基于主从博弈的主动防御策略制定方法，主要结论如下。

(1)本文所提模型可以很好地模拟电力系统相关部门(防御方)与电网元件并发故障(攻击方)之间的相互作用关系。

(2)该模型可先转化为下层为混合整数线性规划的双层优化问题，可采用枚举树算法进行求解，最优解即对应主从博弈的Stackelberg均衡。因此，本文方法所得最优防御策略可以充分考虑电网元件并发故障与后续安全调度的影响，足以应对可能发生的最坏故障情况。

(3)不同于以往的防御策略制定，本文提出的方法在未知系统故障的情况下未雨绸缪，变被动挨打为主动出击，从规划的角度对系统进行主动防御，更加有效降低系统故障所造成的损失。

［1］梅生伟，刘锋，薛安成(Mei Shengwei，Liu Feng，Xue Ancheng)．电力系统暂态分析中的半张量积方法(Semi-tensor product for power system transient analysis) ［M］．北京:清华大学出版社(Beijing:Tsinghua University Press)，2010．

［2］梅生伟，薛安成，张雪敏 (Mei Shengwei，Xue Ancheng，Zhang Xuemin)．电力系统自组织临界特性与大电网安全 (Power system security and self-organized criticality)［M］．北京:清华大学出版社(Beijing:Tsinghua University Press)，2009．

［3］Mei Shengwei，Zhang Xuemin，Cao Ming．Power grid complexity［M］．Springer Press，2011．

［4］张振安，张雪敏，曲昊源，等 (Zhang Zhen’an，Zhang Xuemin，Qu Haoyuan，et al．)．适用于连锁故障的交直流电网静态等值方法 (Equivalent approach for AC/DC power systems cascading failure analysis)［J］．电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2014，33(3):1-6．

［5］Brown G，Carlyle M，Salmeron J，et al．Defending critical infrastructure［J］．Interfaces，2006，36(6):530-544．

［6］Alvarez R E．Interdicting electrical power grids［D］．Monterey:Naval Postgraduate School，2004．

［7］Arroyo J M．Bilevel programming applied to power system vulnerability analysis under multiple contingencies［J］．IET Generation，Transmission＆Distribution，2010，4 (2):178-190．

［8］Natalia Alguacil，Andrés Delgadillob，Arroyo J M．A trilevel programming approach for electric grid defense planning［J］．Computers＆Operations Research，2014，41: 282-290．

［9］Yiming Yao，Thomas Edmunds，Dimitri Papageorgiou，et al．Trilevel optimization in power network defense［J］．IEEE Transactions on Systems，Man，and Cybernetics—Part C:Applications and Reviews，2007，37(4):712-718．

［10］Wei Yuan，Long Zhao，Bo Zeng．Optimal power grid protection through a defender-attacker-defender model［J］．Reliability Engineering and System Safety，2014，121: 83-89．

［11］Liang Yile，Mei Shengwei，Liu Feng，et al．Blackout model for hybrid AC/DC power system［A］．Chinese Control Conference［C］．Nanjing，China，2014.2835-2839．

［12］Scaparra M P，Church R L．A bilevel mixed-integer program for critical infrastructure protection planning［J］．Computers＆ Operations Research，2008，35:1905-1923．

［13］Luis Baringo，Antonio J Conejo．Transmission and wind power investment［J］．IEEE Transactions on Power Systems，2012，27(2):885-893．

［14］S Jalal Kazempour，Antonio J Conejo，Carlos Ruiz．Strategic generation investment using a complementarity approach［J］．IEEE Transactions on Power Systems，2011，26(2):940-948．

［15］Tian Fang，Zhang Xing，Liang Yile，et al．Taxing strategies for carbon emissions based on Stackelberg game ［A］．Chinese Control Conference［C］．Nanjing，China，2014.7607-7611．

Stackelberg game model for active defending strategy in hybrid AC/DC power system

ZHANG Zhen-an1，HUANG Shao-wei2，LIANG Yi-le2，ZHAO Yang1
(1．Henan Province Electric Power Research Institute，SGCC，Zhengzhou 410100，China; 2．State Key Lab of Control and Simulation of Power Systems and Generation Equipment，Department of Electrical Engineering，Tsinghua University，Beijing 100084，China)

With the hybrid AC/DC power system gradually coming into being，the security of the system is increasingly important．It is essential to identify the vulnerable components and to make defending strategies to prevent cascading failures．This paper proposes a Stackelberg game model for active defending strategy in AC/DC power system，i．e．D-A-D tri-level programming model．The upper-level model determines the active defending strategy，the middle decides the multiple contingencies，and the lower represents the security dispatch process．This model can be transformed into a bi-level model whose lower-level is a mixed integer linear programming problem．Thus it can be solved by an enumeration tree algorithm．Simulations and analysis have been conducted in an IEEE 30 bus system to prove its rationality and validity．

power system;active defense;Stackelberg game;tri-level model

TM732

A

1003-3076(2015)10-0010-07

2014-11-08

国家自然科学基金创新研究群体科学基金(51321005)、国家自然科学基金(51377091)资助项目

张振安(1974-)，男，河南籍，高级工程师，硕士，主要从事电力系统稳定性分析、大电网仿真分析方面研究;黄少伟(1985-)，男，福建籍，助理研究员，博士，主要研究方向为电力系统建模与仿真、电力系统安全防御(通信作者)。