利用固有频率异常值分析法检测螺栓拧紧力

缑百勇，陆秋海，王波，王世英

(1.清华大学航天航空学院，北京100084;2.空军工程大学航空航天工程学院，西安710038)

利用固有频率异常值分析法检测螺栓拧紧力

缑百勇1，2，陆秋海1，王波1，王世英1

(1.清华大学航天航空学院，北京100084;2.空军工程大学航空航天工程学院，西安710038)

为了定量评估螺栓松动损伤程度，依据统计学中的马氏平方距离(Squared Mahalanobis Distance，MD)异常值分析法，研究了综合利用结构前5阶固有频率(称为固有频率矢量)检测螺栓拧紧力的方法。首先测试了不同拧紧力下结构的固有频率;然后计算了各拧紧力工况与紧固工况固有频率矢量间的标准欧几里德距离(Standard Euclidean Distance，SED)，利用Matlab拟合了SED与拧紧力之间的关系曲线，据此提出了定量检测螺栓拧紧力的方法;最后对该方法进行了试验验证和应用举例。结果表明，固有频率矢量的SED与拧紧力呈指数关系，而且利用此关系曲线能够比较可靠地评估螺栓松动程度。

螺栓松动;损伤检测;结构健康监测;固有频率;异常值分析;标准欧几里德距离

螺栓连接与铆接、焊接、胶结等结构连接形式相比较，能够承受大的载荷而且可重复装配和拆卸，所以被大量用于连接可拆卸的主承力结构［1］。航空(天)器、建筑工地的吊塔、海洋平台的支撑架以及钢架桥等工程结构的主体受力部分基本都是通过螺栓连接的。因为预紧力可以提高螺栓连接的可靠性、防松能力和螺栓的疲劳强度，增强连接的紧密性和刚性，所以很多结构对螺栓预紧力有严格的要求。结构服役前，螺栓都按照要求处于拧紧状态。然而，在长期的服役过程中，由于受到疲劳、振动、冲击等各种载荷的作用，结构的连接螺栓有可能会逐渐松动(表现为螺栓拧紧力的下降)，轻者造成设备故障，重则结构完全破坏，从而导致严重的灾难。因此需要发展一种无损检测方法在线评估螺栓连接的实际状态［2］。

徐超等［3］和Wang等［4］分别就螺栓松动损伤检测方法进行了回顾和总结。提及的方法概括起来主要分四类:①基于声弹性效应的方法。该方法利用螺栓的声弹性特性会随螺栓拧紧力的变化而发生改变这一现象来检测螺栓的预紧力［5－7］。其缺点是对信号采集设备的采样频率要求很高(约1 Gs/s)，不但设备昂贵，而且高频信号易受噪声的干扰。②基于压电传感器的方法。该方法又可分为基于压电导纳(阻抗)的方法和基于能量的方法。前者早期被Sun等［8］用在桁架结构连接处的松动识别上，王丹生等［9］和高峰等［10］则将其用在螺栓松动损伤的检测上。该方法通过检测紧贴在结构上的压电陶瓷片的电阻抗(或导纳)来反映结构阻抗的变化，从而实现对基体结构上螺栓松动与否的识别。Wang等［11］则对基于能量的方法进行了研究。该方法利用了主动传感技术，将螺栓连接构件一侧的压电片作为激励源，另一侧的压电片作为拾能器，根据两个压电片之间传递能量的大小反映螺栓松紧程度。基于压电传感器的方法利用的也是高频信号，除了设备昂贵、易受干扰之外，传感器与被测结构连接的可靠性和耐久性问题也需要解决。③基于非线性动力学理论的方法。在较大外激励作用下，螺栓松动造成结构连接处界面分离，产生非线性动态响应，直接利用结构的非线性动态响应信号，基于非线性动力学理论方法提取描述结构损伤本质的特征参数，建立起结构损伤状态与非线性特征参量之间的关系，进而进行状态监测和辨识。如Timothy等［12］基于混沌理论研究了螺栓松动状态的识别问题。这类方法测试原理和测试设备都很复杂，不便于工程应用。④基于线性动力学理论的方法。结构损伤会引起结构动力学参数(如固有频率、振型、阻尼、曲率模态、频响函数、功率谱等)的变化，测得这些动力学参数变化量可反推结构的损伤状态。杨智春等［13－14］、Cawley等［15］和Liang等［16］的研究即可归为此类方法。

由于结构动力学参数测试方便而且精度高［17－18］，所以，成为状态监测和识别的经典方法。不过，利用结构动力学参数识别螺栓松动损伤的研究中，大都将螺栓分为“松”和“紧”两种状态来研究，定量检测拧紧力的文献还很缺乏。

本文从统计学中基于马氏平方距离(the squared Mahalanobis Distance，MD)的异常值分析法出发，提出了一种基于结构前5阶固有频率标准欧几里德距离(Standard Euclidean Distance，SED)的螺栓松动定量检测方法，并进行了试验验证和应用举例。

1 基于SED的异常值分析法

在基于数据驱动的损伤检测方法中，如果将结构完好情况下测得的特征参数定义为正常数据，损伤情况下测得的特征参数定义为异常数据，损伤检测的本质就是从实测的大量数据中将异常数据分离出来，并尽可能从异常数据中提取更多有关损伤的信息(损伤程度、损伤位置等)。由于受测量误差等因素的影响，实测数据存在一定的分散性，即使结构在完好情况下，每次测得的特征参数数据也不可能完全一样，这给异常数据的分离带来了困难。基于马氏平方距离的异常值分析法正是解决这一问题有效方法。

如果实测特征参数是一个单变量分布，其均值为μ，标准差为σ，则样本x到均值的距离有两种定义方式;①x－μ，称为绝对距离，②(x－μ)/σ，称为相对距离。显然，相对距离是一种标准化的距离，不仅反映了该样本与均值的差别程度，还可从分布概率的角度反映出该样本在所有样本中的“位置”。

拓展开来，对一个均值为μ，协方差矩阵为Σ的多变量分布而言，其样本x到均值的相对距离可以定义为Z=L－1(x－μ)，其中有LLT=Σ。该定义不仅考虑了各变量的分布情况，还考虑了不同变量之间的相互影响。为了去掉计算中的平方根计算，取上述相对距离的平方值，即定义D=ZTZ，则

最后一行即为马氏平方距离的定义。

要将马氏平方距用在损伤检测中，首先要从实测的数据中提取能够反映损伤状态的多变量特征参数(本文以结构前5阶固有频率组成的向量为特征参数)。假设实测多变量特征参数由p个变量组成，且有n个观测值，则可看作一个p维空间的n个测点，也可以表示为p×n维的矩阵。利用上述定义，第i个测点的马氏平方距离为:

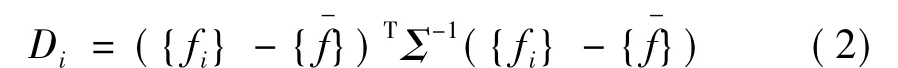
式中:Di为异常值指标;{fi}为实测p维变量{f}的第i次测量值，为可能异常的p维矢量，例如不同时期得到的结构前p阶固有频率矢量;{f}和Σ分别为实测的n个p维变量{f}的平均值矢量和协方差矩阵。T代表转置运算。Di与某种给定的异常值阈值进行比较，大于阈值的即判断为异常，而且从文献［19］可以看出，Di越大，代表偏离正常情况越远［20］。

如果只考虑各变量的分布而不考虑各变量之间的相互影响，马氏距离可进一步简化成为标准欧几里德距离，其定义为:

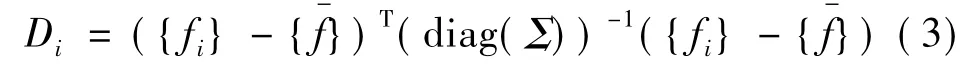
其中，diag(Σ)表示协方差矩阵Σ的对角矩阵。标准化欧几里德距离因为归一化协方差矩阵为对角阵，计算量比马氏平方距离要少很多，但却保留了对异常值很好的检测能力。

实际使用过程中，异常值如果是非先验已知的，往往进行的是内插异常值检测，即待检测的测量矢量参与计算统计平均值，包括均值和方差等;如果有先验已知的无损伤数据，则可以采用外推方式对可能异常的矢量进行异常值检测。

2 螺栓松动定量检测方法及其验证

下面以单螺栓连接的悬臂梁为例，介绍螺栓松动程度的定量检测方法。

2.1 试验装置

如图1所示，试验件由两个金属长梁搭接而成，搭接部分通过一个精制不锈钢螺栓(M10(A2－70))贯穿连接;试验件右端固定在基础上，左端自由，成为一个悬臂梁;距试验件左端10 mm的位置上、下表面分别设置测点和激励点。

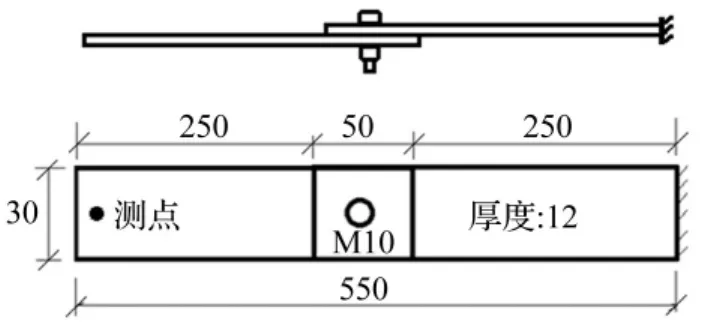
图1 试验件及测点设置示意图Fig.1 Schematic of test structure

用激振器(SINOCERA JZK－5)激励试件，并用加速度传感器(PCBM352)在测点拾振，用LMSTest.Lab 12A模态测试仪及附带软件(Spectral Testing)测量系统的前5阶弯曲固有频率。测试现场见图2。

图2 测试现场照片Fig.2 Specie and test instruments

2.2 试验过程

(1)将螺栓完全拧紧(拧紧力矩为24 N·m)，采用随机激励方式，测得拧紧工况下悬臂梁的前5阶固有频率30组。这些数据用于计算初始状态下固有频率矢量的平均值矢量{f}和协方差矩阵的对角矩阵diag(Σ)。

(2)调整螺栓的拧紧力矩分别为24 N·m、15 N·m、5 N·m和手紧状态，测量结构的前5阶固有频率各5组。其中，除了手紧状态外，其余状态均用力矩扳手调整。测试工况及对应测量次数见表1。这部分数据用于寻求固有频率矢量的标准欧几里德距离与拧紧力的关系。

表1 用于数据拟合的工况和测量次数Tab.1 Bolt conditions and No.of tests for curve fitting

(3)再次调整螺栓的预紧力分别为24 N·m、20 N·m、15 N·m、10 N·m、5 N·m和手紧状态，测量结构的前5阶固有频率各5组。测试工况及对应测量次数见表2。这部分数据用于分析拧紧力和单一模态固有频率之间的关系以及后期的试验验证。

表2 验证工况和测量次数Tab.2 Bolt conditions and No.of tests for verification

2.3 SED和螺栓拧紧力的关系

设拧紧工况下测得的30组5维固有频率矢量分别为{f1}，{f2}，…，{f30}，计算这30组矢量的平均值矢量{˜f}和协方差矩阵的对角矩阵diag(Σ)，然后根据式(3)，分别计算这30组矢量的SED值，结果见图3。显然，各样本的SED值是随机分布的。这种计算方法属于内插法。

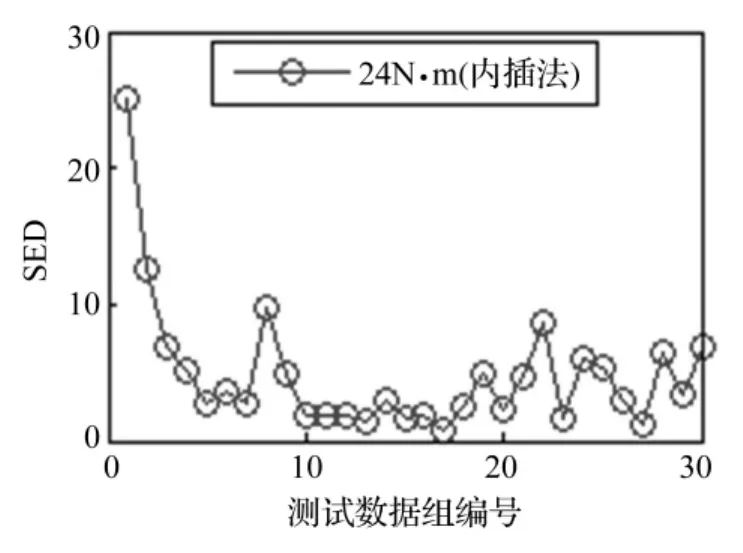
图3 参考样本的SED值Fig.3 SED values of initial state

将表1中24 N·m工况对应的5组测量结果分别代入式(3)，得到5个SED值(这5个数据点是外推法计算的结果)，将其与图3的30个SED值绘制在一起，见图4。从图4可知，用外推法得到的这5个数据与前面30个内插法得到的数据混在一起时并不能将它们分离出来。这是合乎情理的，因为它们所代表的工况都是24 N·m的拧紧力矩。

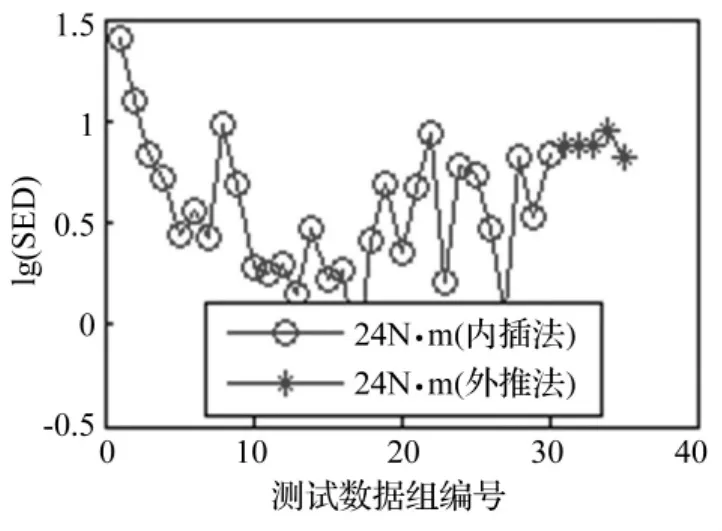
图4 内插法和外推法比较Fig.4 SED values of inclusive and exclusive

再用外推法求得表1中其它各工况对应的SED值，将结果与前期得到的数据一起绘制在图5中。从图5中可知:①4种拧紧力矩状态对应的SED之间区分明显，没有混淆现象出现;②同一种拧紧力矩状态对应的SED相互之间差别很小;③SED随着拧紧力矩的减小单调地增大。

为了进一步寻找SED与拧紧力矩之间的量化关系，将表1各工况对应的20个SED值与拧紧力矩值用Matlab软件进行曲线拟合，得到如图6示的一个指数曲线。该曲线直观地揭示了SED与拧紧力矩之间的量化关系，可以用作螺栓拧紧力矩的预测曲线，即螺栓松动损伤检测的参考曲线。

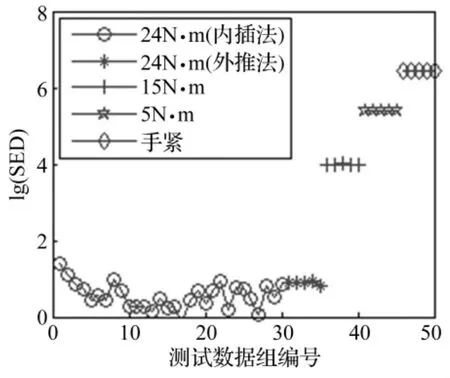
图5 4种工况对应的SED值Fig.5 SED values of table1

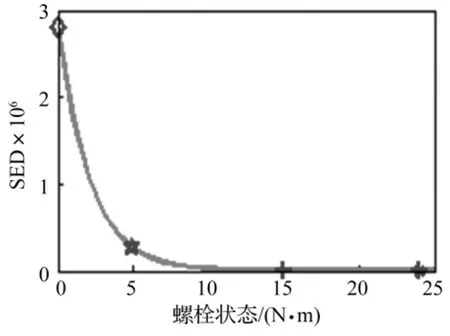
图6 SED与拧紧力矩的关系曲线Fig.6 Curve of SED and tightening forces

2.4 利用SED评估螺栓松动程度的方法

根据以上分析，利用结构前5阶固有频率评估螺栓松动程度的方法归纳如下:

(1)测试拧紧状态的固有频率若干组，组成一个固有频率矢量矩阵，计算该矩阵的平均矢量和协方差矩阵。其中样本数必须不小于矢量的维数。

(2)测试有限几种拧紧力工况的固有频率矢量，用外推法分别计算各矢量到上述平均矢量之间的SED值，拟合各工况所得SED值与拧紧力之间的关系曲线，作为损伤程度检测的参考曲线。

(3)测试待测状态下结构的固有频率矢量，计算其与上述平均矢量之间的SED值，然后将得到的结果与参考曲线进行比较，给出待测状态的螺栓拧紧力估计值。

其中前两步属于基础性的工作，需要在结构正式服役前进行。

2.5 试验验证

将表2中6种工况共30组测量数据依次代入式(3)，用外推法求得对应的30个SED值，将其与紧固工况内插法得到的30个SED一起绘制在图8中。比较图7与图5可知，图7反映出与图5相同的规律。再将表2中6种工况对应的30个SED值和图6中的参考曲线绘制在一起(见图8)。从图8可知，用于验证的6组共30个数据与参考曲线吻合良好(最大误差出现在10 N·m的位置，绝对误差约为4 N·m)，从而证明了该方法的合理性。

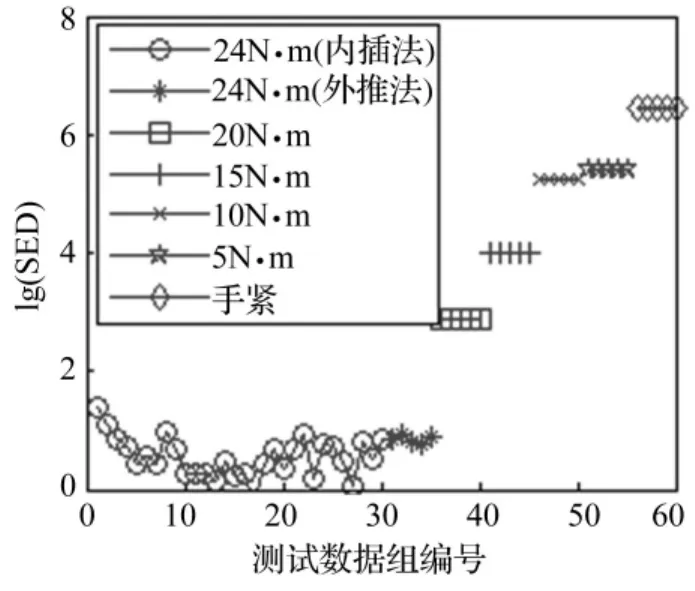
图7 验证样本的SED值Fig.7 SED values of table2

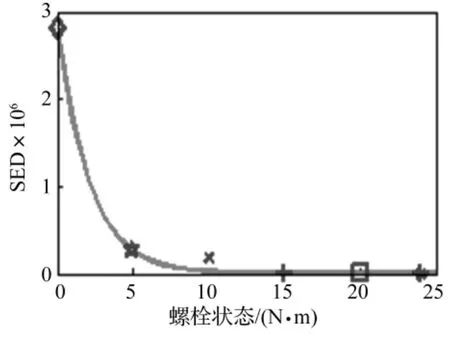
图8 验证数据点与参考曲线对比图Fig.8 Curve and verification points

3 应用举例

为了探讨上述方法在多螺栓连接情况下的有效性，将其应用在某一卫星太阳帆板实物模型的螺栓松动定量化检测过程之中。

3.1 试验装置

卫星太阳帆板通过夹具固定在基础上(见图9和图10)。太阳帆板和夹具通过四个M6的螺栓连接，螺栓设计工作状态的拧紧力矩为12 N·m。

图9 试验件及测点示意图Fig.9 Schematic of test structure

图10 测试现场照片Fig.10 Specie and test instruments

3.2 测试参考曲线

参考曲线的测试在太阳帆板模型的装配过程中进行。首先，将四个螺栓用手均匀拧紧。然后，用力矩扳手将各螺栓的拧紧力矩调整到3N·m，调整方法参考文献［21］中的方法进行，以保证各个螺栓的拧紧力矩相等，测试结构的固有频率5组。再用相同的方法分别测试4 N·m、8 N·m工况下的固有频率各5组，以及12 N·m工况下的固有频率35组。最后利用前述方法计算各工况的SED值并拟合参考曲线(见图11)。

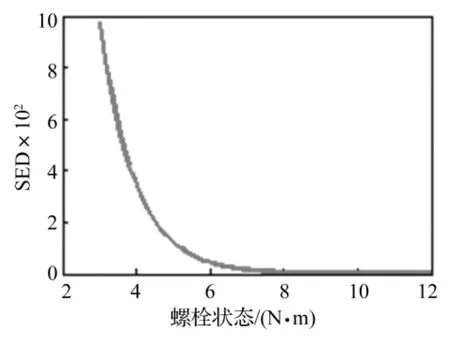
图11 SED与拧紧力矩的关系曲线Fig.11 Curve of SED and tightening forces

3.3 检测效果

选用三种工况测试文中提出的方法对多螺栓结构的检测效果。

工况1:四个螺栓都松至10 N·m;

工况2:四个螺栓都松至6 N·m;

工况3:两侧螺栓均松至4 N·m，中间两个螺栓保持6 N·m。

在每种状态测试结构的固有频率各5组，利用式(3)计算SED指标，并与曲线对比，得出拧紧力矩评估结果(由于每种状态有5组数据，所以可得到5个评估结果)。评估结果与实际拧紧力矩的对比见表3。

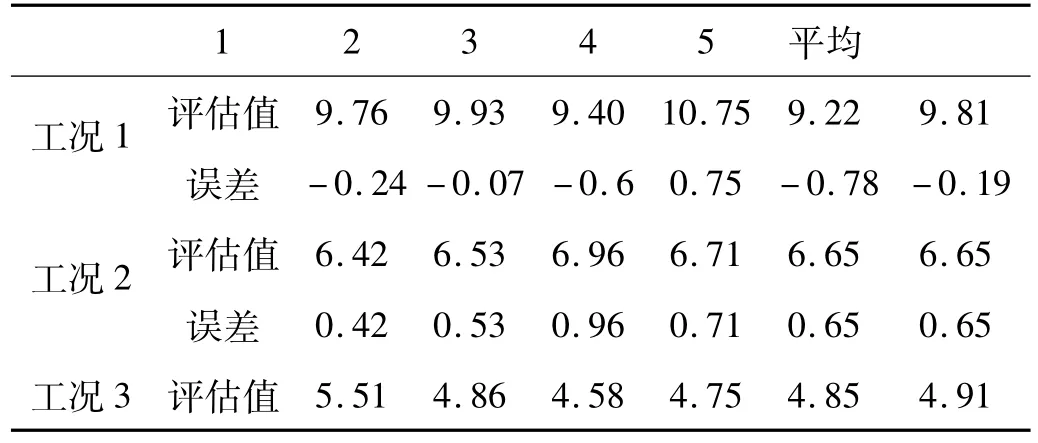
表3 拧紧力矩评估结果与实际值对比情况(单位:N·m)Tab.3 Comparison between test results and actual values(Unit:N·m)

从表3可知，工况1时，最大误差为－0.78 N·m，如果利用5次测量的平均值，误差为－0.19 N·m;工况2时最大误差为0.96 N·m，如果利用5次测量的平均值，误差为0.65 N·m;曲线虽不具备检测工况3情况的能力，但工况3的平均在参考曲线上对应的预紧力矩值(4.91 N·m)介于6 N·m和4 N·m之间，体现了一种“等效损伤”程度。

4 结论

本文提出了一种利用结构前5阶固有频率的SED进行螺栓拧紧力定量评估的方法。通过上述研究，可以得出以下结论:

(1)结构前5阶固有频率的SED值与螺栓拧紧力矩呈指数关系;

(2)文中提出的方法不仅适用于单螺栓连接结构，对多螺栓连接结构也有一定的检测能力。

此外，就相关问题讨论如下:

(1)通过对太阳帆板模型的检测结果可以发现，同一种状态，用多次测量得到的固有频率分别进行识别，其结果有一定的分散性，所以可取平均值作为最终的评估结果。

(2)该方法目前对各螺栓拧紧力矩相同情况的定量评估效果较好;另外，通过对太阳帆板工况3情况的检测说明，对不同预紧力情况也有一定的“等效损伤”检测能力;但对于更为复杂的情况和更高的检测要求则需要进一步的研究，与其他局部检测方法相结合是一个探索的方向。

(3)固有频率反映的是结构的总体特性，而螺栓松动是结构的局部性能变化，要从固有频率变化检测螺栓的松动程度需满一定的条件——局部性能变化影响到了结构的总体特性。从参考曲线可以看出，在螺栓松动程度不大时，对结构总体特性影响较小，所以曲线很平缓，此时该方法的检测精度一般比较低;当螺栓松动到一定的程度，就会对结构总体特性有较大的影响，对应于曲线中相对陡峭的部分，此时该方法可以得到较准确的结果。

(4)如果不需要量化评估，只是简单的趋势监测，则无需参考曲线，以任何一个状态作为起始状态，用式(3)计算之后各时间节点测得的特征参数矢量的SED值，并进行基于时间的趋势分析即可。这样能够拓展该方法的应用范围。

［1］中国航空研究院.复合材料结构设计手册［M］.北京:航空工业出版社，2001.

［2］向志海，黄俊涛.螺栓松紧程度的受控敲击检测方法［J］.试验力学，2012，27(5):545－551.

XIANG Zhi－hai，HUANG Jun－tao.A controlled tap detection method for bolt tightness［J］.Journal of Experimental Mechanics，2012，27(5):545－551.

［3］徐超，周帮友，刘信恩，等.机械螺栓连接状态监测和辨识方法研究进展［J］.强度与环境，2009，36(2):29－36.

XU Chao，ZHOU Bang－you，LIU Xin－en，et al.A review of vibration－based condition monitoring and identification for mechanical bolted joints［J］.Structure＆Environment Engineering，2009，36(2):29－36.

［4］Wang Tao，Song Gang－bing，Liu Shao－peng，etal.Review of bolted connection monitoring［J］.International Journal of Distributed Sensor Networks，2013，871213(8pages).

［5］Yasui H，Kawashima K.Acoustoelastic measurement of bolt axial load with hypothetical velocity ratio method［J］.Transactions of the Japan Society of Mechanical Engineers A，2000，66(642):390－396.

［6］Chaki S，Corneloup G，Lillamand I，et al.Combination of longitudinal and transverse ultrasonic waves for in situ control of the tightening of bolts［J］.Journal of Pressure Vessel Technology，2007，129(3):383－390.

［7］Joshi SG，Pathare R G.Ultrasonic instrument formeasuring bolt stress［J］.Ultrasonics，1984，22(6):270－274.

［8］Sun F P，Chaudhry Z，Liang C.Truss structure integrity identification using PZT sensor－actuator［J］.Journal of Intelligent Material Systems and Structures，1995，6:134－139.

［9］王丹生，朱宏平，鲁晶晶，等.基于压电导纳的钢框架螺栓松动检测试验研究［J］.振动与冲击，2007，26(10):157－160.

WANG Dan－sheng，ZHU Hong－ping，LU Jing－jing，et al.Experimental study on detecting loosened bolts of a steel frame based on piezoelectric admittance［J］.Journal of Vibration and Shock，2007，26(10):157－160.

［10］高峰，王德俊，江钟伟，等.压电阻抗技术用于螺栓松紧健康诊断［J］.中国机械工程，2001，12(9):1048－1049.

GAO Feng，WANG De－jun，JIANG Zhong－wei，et al.Research on piezoelectric impedance technology for bolt health monitoring［J］.China Mechanical Engineering，2001，12(9):1048－1049.

［11］Wang Tao，Song Gang－bing，Wang Zhi－gang.Proof－ofconcept study of monitoring bolt connection status using a piezoelectric based active sensing method［J］.Smart Materials and Structures，2013，22:1－5

［12］Fasel TR，Todd M D，Park G.Active chaotic excitation for bolted jointmonitoring［C］//Proceeding of SPIE，Sensors and Smart Structures Technologies for Civil，Mechanical，and Aerospace System.Conference，San Diego，California，USA，2006，6174:61741S1－61741S8.

［13］杨智春，张慕宇，王乐.飞机加筋壁板紧固件松脱损伤检测的自相关分析方法［J］.振动与冲击，2011，30(11):13－16.

YANG Zhi－chun，ZHANG Mu－yu，WANG Le.Damage detection of fastener loosening of aircraft stiffened panel by auto correlation analysis［J］.Journal of Vibration and Shock，2011，30(11):13－16.

［14］杨智春，于哲峰.飞机壁板紧固件松脱损伤检测的实验研究［J］.应用力学学报，2008，25(1):99－102.

YANG Zhi－chun，YU Zhe－feng.Experimental research on detection in fastener－loosing of aircraft panel by correlation function［J］.Chiness Journal of Applied Mechanics，2008，25(1):99－102.

［15］Cawley P，Adams R D.The location of defects in structures from measurements of natural frequencies［J］.Journal of Strain Analysis，1979，14(2):49－57.

［16］Liang R Y，Member，ASCE，et al.Theoretical study of crack－induced eigenfrequency changes on beam structures［J］.Journal of Engineering Mechanics，1992，118(2):384－396.

［17］高维成，刘伟，邹经湘.基于结构振动参数变化的损伤探测方法综述［J］.振动与冲击，2004，23(4):1－7.

GAO Wei－cheng，LIU Wei，ZOU Jing－xiang.A review of damage detecting methods based on changes of structural vibrationparameters［J］.Journal of Vibration and Shock，2004，23(4):1－7.

［18］Adams R D，Cawley P，Pye C J.A vibration technique for non－destructively assessing the integrity of structures［J］.Journal of Mechanical Engineering Science，1978，20(2): 93－100.

［19］Worden K，Manson G.Damage detection using outlier analysis［J］.Journal of Sound and Vibration，2000，229(3): 647－667.

［20］Nguyen T，Chan T H T，Thambiratnam D P.Controlled Monte Carlo data generation for statistical damage identification employing Mahalanobis squared distance［J］.Structural Health Monitoring，2014，13(4):461－472.

［21］He K，Zhu W D.Detecting loosening of bolted connections in a pipeline using changes in natural frequencies［J］.Journal of Vibration and Acoustics，2014，136:034503－1－034503－7.

［22］Ritdumrongkul S，Abe M，Fujino Y，et al.Quantitative health monitoring of bolted joints using a piezo ceramic actuator－sensor［J］.Smart Materials and Structures，2004，13:20－29.

Bolt tightening force detection using outlier analysis of structural natural frequencies

GOU Bai－yong1，2，LU Qiu－hai1，WANG Bo1，WANG Shi－ying1
(1.School of Aerospace，Tsinghua University，Beijing 100084，China; 2.Aeronautic and Astronautic Engineering College，Air Force Engineering University，Xi'an 710038，China)

In order to evaluate the severity of bolt looseness quantitatively，a study was made to detect bolt tightening force using structural first 5 natural frequencies and the squared mahalanobis distance(MD)outlier analysis.Firstly，the structural natural frequencies under different tightening force condition weremeasured，and then，the standard euclidean distances(SEDs)between the natural frequency vector under fully－tightening condition and those under several not－fully－tightening conditionswere calculated.The fitting curve for SEDs and tightening forces wasmade using Matlab，and amethod was proposed to detect tightening force.Test verification and application examples were given at last.The results showed that there is an exponential relationship between SEDs and tightening forces，this relationship can be used to evaluate the severity of bolt looseness reliably.

bolt looseness;damage detection;structural health monitoring(SHM);natural frequency;outlier analysis;standard euclidean distance

TB123;TH113.1

A

10.13465/j.cnki.jvs.2015.23.014

国家自然科学基金资助项目(11090334，11372154)

2014－09－22修改稿收到日期:2014－12－03

缑百勇男，博士生，讲师，1976年生

陆秋海男，博士，教授，1970年生