低雷诺数下五圆柱绕流的数值模拟研究

朱润野，刁明军，刘 伟

(1.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610064;2.四川水利干部学校，四川 成都 610072)

低雷诺数下五圆柱绕流的数值模拟研究

朱润野1，刁明军1，刘 伟2

(1.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610064;2.四川水利干部学校，四川 成都 610072)

基于四叉树自适应网格，采用有限体积法求解二维不可压粘性N-S方程，对X型排列和十字型排列的五圆柱绕流进行了模拟，计算均在Re=100的条件下进行.在文中给出了升力系数及阻力系数随圆柱间距比和排列方式变化的规律，并结合不同间距比下的流动特征进行了分析.计算结果表明，在不同的间距比下，五圆柱绕流存在三种不同的流动形式;在同一间距比下，十字型布置和X型布置的流动形式则既有类似之处又有各自的特点.在不同排列方式下，升阻力系数随圆柱间距比的变化规律有较大不同.

五圆柱绕流;四叉树网格;数值模拟;升力系数;阻力系数

在工程应用中，多圆柱绕流现象十分常见，如海洋石油平台桩柱、斜拉桥拉索、海底输油管线、电厂冷却塔群、桅杆、天线等.同时，因为当流体流过多圆柱时，由于各个圆柱之间存在相互影响，多圆柱绕流往往会出现复杂且多样的流动形态，与单圆柱绕流十分不同，故针对多圆柱绕流的研究有着广泛的实际意义.

前人对多圆柱绕流的研究往往集中在双圆柱、三圆柱和四圆柱绕流.对双圆柱绕流问题，Willianmson［1］通过实验，研究了并列双圆柱后的尾流演变;郑庭辉等［1］采用有限体积法对，对雷诺数为100～300的串列双圆柱的尾流进行了研究.顾志福和孙天风［3］采用实验的方法，对雷诺数为5.5×104和1.4×104的三圆柱绕流问题进行了研究.Yan Bao等［4］采用二阶CBS有限元算法对呈正三角形排列的圆柱绕流问题进行了研究，并进行了有益的讨论.Lam［5］通过实验，研究了亚临界雷诺数下，四圆柱绕流的流动情况，同时采用有限体积法模拟了三维情况下的四圆柱绕流问题［6－12］.

国内外对五圆柱绕流问题的研究非常少见，考虑到五圆柱绕流问题在实际工程中的潜在价值，对其的研究具有一定的意义.本文利用数值方法，对低雷诺数下，两种不同排列方式的五圆柱绕流问题进行了研究，给出了在不同间距比下一些重要的流动参数，并对流态进行了分析.

1 数值模型

1.1 控制方程

二维不可压粘性非定常流动运动方程为

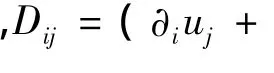
1.2 数值方法

采用分步预估法离散时间项，控制方程可写作:

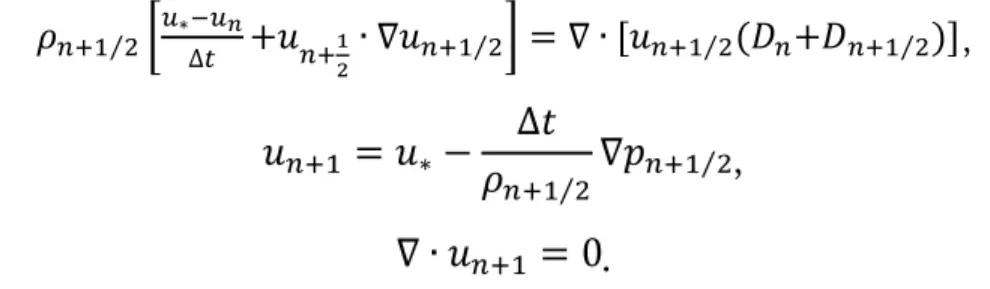
采用二阶迎风格式离散对流项.该方法在时间及空间上均具有二阶精度.具体细节参考文献［7］［8］.

1.3 计算区域及边界条件

本文讨论的五圆柱的布置情况分为X型分布和十字型分布，如图1(a)和图1(b)0～4分别代表五个柱的编号，下文以C0～C4指代，其中C0为位于中间的圆柱.L代表两个圆柱之间的距离.五个圆柱具有相同的直径，用D表示圆柱的直径.

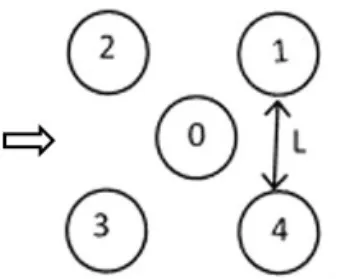
图1(a)X型布置Fig.1(a)Five cylinders in X arrangement

图1(b) 十字型布置Fig1.(b)Five cylinders in cruciform arrangement

计算区域及边界条件如图1(c)所示.为了尽可能减少边界的影响，在y方向上宽度为50D，在x方向上长度为70D.在圆柱表面采用无滑移边界条件.

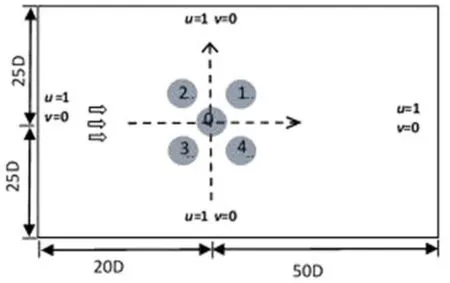
图1(c) 计算区域及边界条件Fig.1(c)Computational domain and boundary condition

本文采用四叉树自适应网格进行计算，网格在计算过程中将根据流速梯度和压力变化自动加密.图2(a)为计算完成后单个圆柱周围的网格;图2(b)为计算完成后计算域的网格.

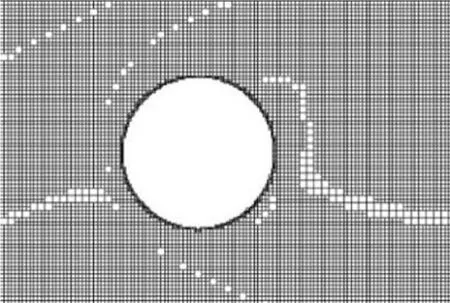
图2(a) 单个圆柱周围网格Fig.2(a)Mesh around single cylinder

图2(b) 计算域网格Fig.2(b)Mesh of computational domain

1.4 升、阻力系数的计算

用Cd和Ci表示圆柱的升、阻力.每个圆柱的升阻力以下标表示.根据文献［5］随时间变化的升阻力定义为:

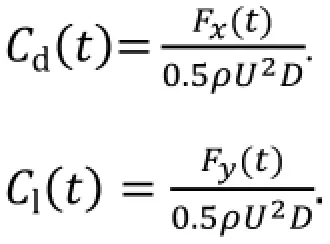
阻力系数和升力系数的时均值和定义为:

阻力系数和升力系数的均方根值和定义为:

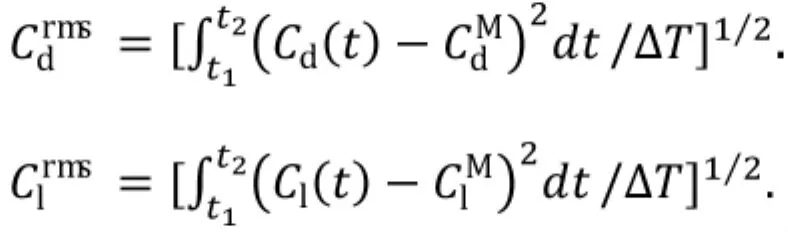
升力系数的峰值定义为:

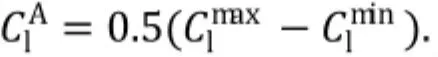
2 数值有效性验证

为了验证计算的有效性，同时为了与五圆柱绕流进行比较，本文计算了在Re=100时单圆柱的绕流问题，计算结果见表1.从表1可知，本文计算与前人结果的最大误差为3.7%，误差较小.

3 流动形式

本文计算了 L/D=1.0，1.5，2.0，2.5，3.0，4.0，5.0等几种间距比情况下的绕流问题，得到了各间距比下的流动形式，以下将根据两种布置分别讨论流动形式随间距比的变化并比较它们之间的异同.

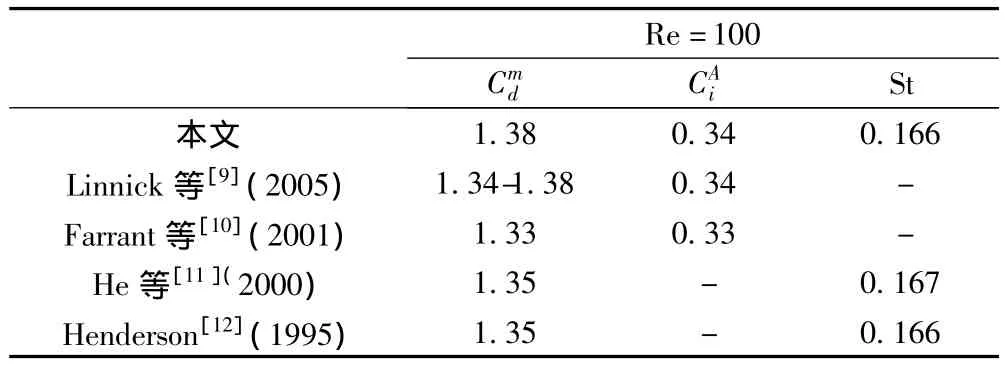
表1 单圆柱绕流计算结果对比Tab.1 Comparisons of mean drag，amplitude of lift force and Strouhal number at Re=100 for single cylinder

3.1 X型布置

在小间距比下，X型布置的流动形式类似于单圆柱绕流.由于圆柱之间间隙流的影响，圆柱C2的尾涡偏向上方，圆柱C3的尾涡偏向下方.

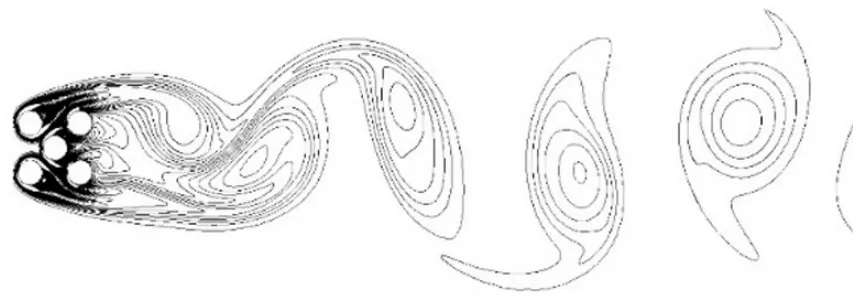
图3 L/D=1时涡量等值线图Fig.3 Snapshot of instantaneous vorticity contours for L/D=1

图4和图5为五圆柱处于中等间距比时，涡量等值线图和流线图.从图4可以看到，C1和C4后的涡呈对称反相脱落.脱落的涡相对于来流方向对称分布.从图5可以看到，由于圆柱C1和C4的影响，中间圆柱C0的尾流受到挤压，并在C0后形成了稳定且对称的回流区.根据文献［13］，当L/D=2时，上游圆柱不会产生涡脱落，其剪切层将附着在下游圆柱上，但在本文的情况中，由于中间圆柱与C2、C3之间的间隙流，C2与C3后的尾流将会偏向柱群外侧，只有C2下边缘的剪切层和C3上边缘的剪切层会附着在下游圆柱上.在远离柱群的下游，上下两侧的涡会相互靠近融合形成单个的涡.

图4 L/D=2时涡量等值线图Fig.4 Snapshot of instantaneous vorticity contours for L/D=2

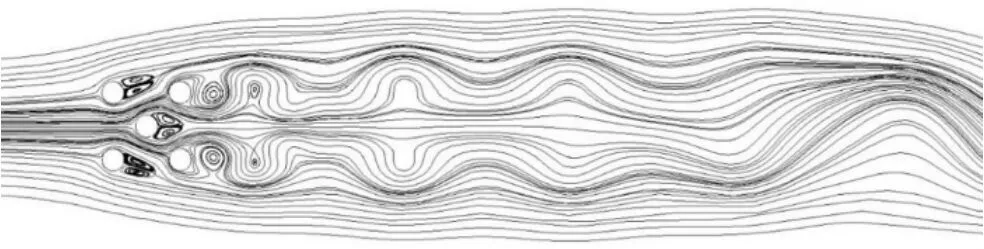
图5L/D=2时流线图Fig.5 Snapshot of streamlines for L/D=2

图6为L/D=4时的涡量等值线图.当间距比较大时，圆柱之间的相互影响减小，在C2、C3和C0后形成了充分发展的涡脱落.圆柱C2和C3的涡呈反相脱落，并会撞击下游圆柱.下游圆柱C1和C4的涡脱落依然会受到中间圆柱C0的影响而变得不规律.C1下缘和C4上缘脱落的涡会偏向中间.C1和C4的脱落的涡在柱群后会形成两条涡带.

图6 L/D=4时涡量等值线图Fig.6 Snapshot of instantaneous vorticity contours for L/D=4

图7为L/D=1.5时的流线图.C1和C4后形成了一大一小两个涡，是因为C1和C4两圆柱间的间隙流偏向C1，从而使C1后的涡受到影响，其尾涡的长度明显短于圆柱C4后的涡.图7(a)和图7(b)为无量纲时间分别为200和225时的流线图，可以看到当两圆柱间的间隙流偏向某一圆柱后，间隙流的偏向就不会再发生改变，形成所谓的单稳态流动.

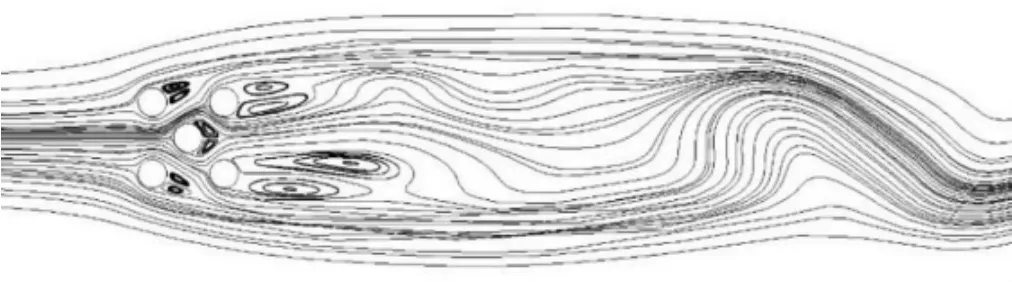
图7(a)Ut/D=200时流线图Fig.7(a)Snapshot of streamlineswhen Ut/D=200

图7(b)Ut/D=225时流线图Fig.7(b)Snapshot of streamlineswhen Ut/D=225

3.2 十字型布置

当间距比较小时，与X型布置类似，十字型布置的流动形态类似于单个圆柱.涡会从C1、C3和C4后产生，并在柱群后一定距离内融合形成一个较大的涡.从图8可以看到，由于圆柱间的距离较近，C2和C0后的涡并没有脱落，而是粘附在圆柱C4上;圆柱C4由于间隙流和周围圆柱涡的影响，分离点前移.

随着间距比的增大，圆柱C1和C3的涡开始脱落，图9为L/D=2时涡量等值线图.C1和C3的涡脱落会影响到C4后的流动，使得C4后的流动较混乱.C4后的涡会与C1和C3后的涡融合.C1和C3后脱落的涡随着流动，很快就会破碎，失去完整的形状.

图8 L/D=1时涡量等值线图Fig.8 Snapshot of instantaneous vorticity contours for L/D=1

图9 L/D=2时涡量等值线图Fig.9 Snapshot of instantaneous vorticity contours for L/D=2

当间距比较大时，受其他圆柱影响较小的圆柱会形成充分发展的涡脱落.图10为L/D=4时的涡量等值线图.可以看到，圆柱C1和C3的涡脱落受中间圆柱的影响减小，并呈反相脱落.圆柱C2的涡开始脱落，并影响到中间圆柱C0.中间圆柱C0后的涡撞击到圆柱C4上，会与圆柱C4的涡融合并使C4的涡脱落更不规则.

4 间距比对升、阻力的影响

图7为X型布置下升、阻力系数随间距比的变化规律.图8为十字型布置下升、阻力系数随间距比的变化规律.根据文献［13－15］，多圆柱绕流问题中，圆柱间的相互影响可分为三类:邻近影响、剪切层影响和尾流影响.以下将基于这三种影响因素，对两种布置下五圆柱绕流问题中，升、阻力系数的变化规律进行分析.

4.1 X型布置

从图11(a)中可以看到，C1和C4的时均阻力系数值小于C2和C3的时均阻力系数值，这是因为当间距比较小时，C1和C4位于上游圆柱剪切层形成的低压区中，圆柱前后缘的压差较小，此时和较小，随着间距比增大，剪切层的影响变小，阻力系数便开始上升.同时来流主要作用在C2和C3上，故C2和C3的时均阻力系数大于C1和C4.圆柱C0由于在小间距比的情况下，部分受到圆柱C2和C3剪切层的影响，故其时均阻力系数较小但大于C1和C4的时均阻力系数和在L/D＞3后有一定下降，这与双圆柱绕流的变化规律一致［16］.

从图11(b)可以看到由于中间圆柱的存在，除去C0外的所有圆柱的时均升力系数不再等于0.而由于流态的对称性，则几乎为0.在间距比2＜L/D＜4时，作用于C2和C3的升力大于作用于C1和C4上的升力.

从图11(c)可以看到，当间距比大于1.5时，和随着间距比增大而增大，但当间距比大于4后则开始下降.这是因为随着间距比的增大，上游圆柱C2和C3后的涡开始脱落，同时C0的涡也开始脱落，脱落的涡撞击到C1和C4上，造成和较大.圆柱C0也会受到C2和C3的影响，故变化规律与C1和C4类似，但大小小于和

从图11(d)可以看到，当间距比1.5≤L/D≤4时，由于C1和C4后的涡脱落和上游圆柱脱落的涡的影响和随着间距比增大而增大和也会在L/D大于某个值后开始增加，并逐渐接近单个圆柱的升力系数均方根值.

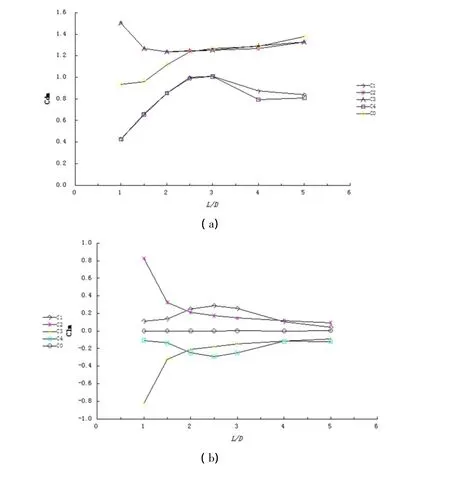
图11 X型布置下升、阻力系数变化规律Fig.11 variation of force coefficients with gap spacing at X arrangement

4.2 十字型布置

图12(a)为时均阻力系数随间距比的变化规律.随着间距比的增加而增加.当L/D小于1.5时，由于C1和C3邻近影响，C1、C3和C0之间的间隙流偏向圆柱C0，在C0前间形成了一个高压区，使得大于，但随着L/D的增大，邻近影响逐渐减小，使得随着L/D的增大而减小，当L/D≥3时又开始增大，并接近于单个圆柱绕流时的时均阻力系数大小.当L/D≤3时接近于0.

图12(b)为时均升力系数随间距比变化的曲线.和的绝对值随着L/D的增大而减小.而和则几乎接近于0.

图12(c)为阻力系数的均方根值随D/L的变化规律.随着L/D的增加突然上升，达到0.174，并且在L/D=2～L/D=4的范围内一直较大，这主要是因为在L/D较小时，C1和C3后脱落的涡影响了C4周围的压力分布，而随着L/D增大，虽然C1和C3的影响减小，但C0后的涡开始脱落，从而持续影响C4周围的压力分布.在L/D=3的位置，C1和C3的影响减小，而C0后的尾流还未充分发展，因此有小幅度的下降.

图12(d)为升力系数的均方根值随L/D的变化规律.和随这L/D的增加而增加，并趋向于单个圆柱的升力系数均方根值大小.当L/D＞3，和突然开始增大，且的值大于，因为C4同时受到C2和C0脱落的涡的影响，而C0只受到C2脱落的涡的影响.

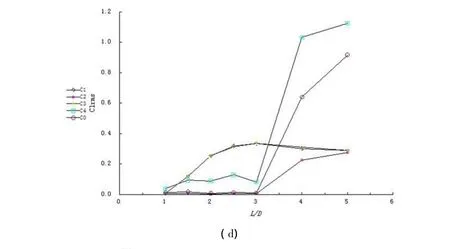
图12 十字型布置下升、阻力系数变化规律Fig.12 variation of force coefficients with gap spacing at cruciform arrangement

5 结论

本文采用在时间和空间上皆具有二阶精度的分步预估法，基于四叉树自适应网格，对Re=100条件下X型布置和十字型布置的五圆柱绕流问题进行了计算，得到了如下结论:

1)低雷诺数下，布置相同的五圆柱，根据L/D的大小可以将流动形式分为三种类型.当L/D较小时，流动形式类似于单个圆柱的绕流，在五圆柱后形成单个脱落的涡.在中等间距下，自柱群上下缘产生涡脱落，而处于中间位置的圆柱由于受到其他圆柱的影响尾流无法充分发展成脱落涡.在大间距比下，柱群中不受上下游影响的圆柱的尾流会充分发展，形成涡脱落.

2)在同一间距比下，两种布置形式的流动形态会有所不同.小间距比下，十字型布置后涡开始脱落的距离要长于X型布置.在中等间距比和大间距比下，两种布置形式后涡的分布有较大区别.对于X型布置，在特定间距比下则会出现单稳态流动.

3)当L/D较小时，升、阻力系数主要受剪切层和邻近圆柱的影响，而当L/D增大，圆柱后的涡开始脱落，脱落涡的影响将逐渐增大，受到上游圆柱脱落涡影响的圆柱，Crmsd和Crms1会增大.当五圆柱呈十字型布置时，存在一临界L/D值，当L/D大于该值时，升、阻力系数的变化规律会与L/D小于该值时的规律有明显不同.该值在本计算中大约在3附近.

4)采用四叉树自适应网格可以减少计算时间，提高计算效率，且对多圆柱绕流问题的计算结果令人满意.

［1］WILLIAMSON C H K.Evolution of a single wake behind a pair of bluff bodies［J］.Journal of Fluid Mechanics，1985，159:1-18.

［2］郑庭辉，费宝玲.串列双圆柱尾迹流的数值分析［J］.西南交通大学学报，2008，43(6):747-750.

ZHENG TING HUI，FEI BAO LING.Numerical analysis of flow around two tandem circular cylinders［J］.Journal of Southwest University for Nationalities 2008，43(6):747-750.

［3］GU Z，SUN T.Classifications of flow pattern on three circular cylinders in equilateral-triangular arrangements［J］.Journal of Wind Engineering＆ Industrial Aerodynamics，2001，89(6):553-568.

［4］BAO Y，ZHOU D，HUANG C.Numerical simulation of flow over three circular cylinders in equilateral arrangements at low Reynolds number by a second-order characteristic-based split finite element method［J］.Computers ＆ Fluids，2010，39(5):882 –899.

［5］LAM K，LI J Y，SO R M C.Force coefficients and Strouhal numbers of four cylinders in cross flow［J］.Journal of Fluids ＆ Structures，2003，18:305–324.

［6］BARANYIL.Lift And Drag Evaluation In Translating And Rotating Non-Inertial Systems［J］.Journal of Fluids＆ Structures，2005，20(1):25–34.

［7］BROWN D L，CORTEZ R，MINION M L.Accurate Projection Methods for the Incompressible Navier-Stokes Equations［J］.Journal of Compu tational Physics，2001，168(2):464 – 499.

［8］POPINET S.Gerris:a tree-based adaptive solver for the incompressible Euler equations in complex geometries［J］.Journal of Computational Physics，2003，190(2):572 – 600.

［9］LINNICK M N，FASEL H F.A high-order immersed interface method for simulating unsteady incompressible flows on irregular domains［J］.Journal of Computational Physics，2005，204(1):157 – 192.

［10］FUJISAWA N，KAWAJI Y，IKEMOTO K.Feedback Control Of Vortex Shedding From A Circular Cylinder By Rotational Oscillations［J］.Journal of Fluids ＆ Structures，2001，15(1):23-37.

［11］HE J-，GLOWINSKI R，METCALFE R，et al.Active Control and Drag Optimization for Flow Past a Circular Cylinder.I.Oscillatory Cylinder Rotation［J］.Journal of Computational Physics，2000，163(1):83-117(35).

［12］HENDERSON R D.Details of the drag curve near the onset of vortex shedding［J］.Physics of Fluids，1995，7(9):2102-2104.

［13］MENEGHINI J，SALTARA F.Numerical Simulation Of Flow Interference Between Two Circular Cylinders In Tandem And Side-By-Side Arrangements［J］.Journal of Fluids ＆ Structures，2001，15(2):327-350.

［14］LAM K，CHEUNG W C.Phenomena of vortex shedding and flow interference of three cylinders in different equilateral arrangements［J］.Journal of Fluid Mechanics，1988，196(196):1-26.

［15］顾志福，孙天风.三圆柱绕流的实验实验研究［J］.空气动力学学报，2000，18(4)，441-447.

GU ZHI FU，SUN TIAN FENG.Experimental Research on Flow A-round Three Circular Cylinders［J］.Acta Aerodynamica Sinica，200，18(4):441-447.

［16］SHARMAN B，LIEN F S，DAVIDSON L，et al.Numerical predictions of low Reynolds number flows over two tandem circular cylinders［J］.International Journal for Numerical Methods in Fluids，2005，47(5):423–447.

Numerical investigation of flow past five circular cylinders at low Reynolds number

ZHU Run-ye，DIAO Ming-jun
(State Key Lab of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu610065，P.R.C.)

In order to have a deeper understanding of flow around multiple circular cylinders，a parallel code which discretizes the 2D incompressible Navier-Stokes equations is employed in this paper and an adaptive octree mesh is also used.The simulation is operated at Re=100.The influence of cylinder-to-cylinder spacing ratio and the arrangements of five cylinders are investigated.The results of the simulation suggested that there were three different flow patterns connected to various spacing ratio;there were also differences between two arrangements of cylinders when the spacing ration was the same.The spacing ration has different effects on the coefficients of drag and lift at X arrangement and cruciform arrangement.

flow pastfive circular cylinders;octree mesh;numerical simulation;fluid force

TV131.4

A

2095-4271(2015)06-0758-09

10.11920/xnmdzk.2015.06.020

2015-09-23

朱润野(1991－)，男，浙江温州人，硕士研究生，研究方向:水工水力学，Email:273216779@qq.com

刁明军(1968－)，男，四川简阳人，教授，博士生导师，研究方向:工程水力学的科研与教学工作.Email:diaomingjun@scu.edu.cn

四川省学术和技术带头人培养基金(2012DTY020)

(责任编辑:付强，张阳，李建忠，罗敏;英文编辑:周序林)